1 Introduction

1.1 Motivation

Due to the increasing use of multi-material designs, clinching is becoming more and more important in industry. It offers advantages in comparison to other joining processes and can overcome their application limits. Clinching is used in the automotive industry or in the production of household appliances, among others. Despite the already widespread use of the process, there is still a need for research to understand the mechanisms and design of clinched joints. In contrast to the tool parameters, process influences and material influences have not yet been investigated to a relatively large extent. It is therefore useful to investigate these influences in order to determine the importance of taking them into account in the design of a clinching point. Simulations can be used to investigate selected process influences. The process influences to be investigated are different sheet thicknesses, the history of the joining partners using the example of pre-hardening of the material as well as their positioning in the process and punch stroke as a possible disturbance variable. With the investigation of the clinching process on the basis of the parameters at the joint, the importance of a comprehensive view of the clinching process is demonstrated. To confirm the simulation results, experimental investigations of the clinching point geometry and the shear strength of the clinched joint are carried out. This investigation is intended to demonstrate the importance of the holistic consideration of the clinching process and the previous manufacturing steps of a component.

1.2 State of the art

1.2.1 Clinching process

Clinching is defined as joining by cold forming of two or more overlapping sheet metals using a punch and a die thereby creating a frictional and form-fit connection without additional connecting elements, additives or auxiliary materials [1]. The main task of clinching is the joining of sheets with thicknesses between 0.5 mm and 3.0 mm [2] and is used in automotive engineering [3], in space travel [4], in civil applications such as bridges [5], electrical household goods [6] and many more. Due to the small tool dimensions, however, clinching is considered a bulk forming process [7]. It is possible to join dissimilar materials in metal-to-metal joints [8] and also metal-to-non-metal joints [9]. The use of dissimilar materials is useful for the lightweight construction, in which suitable materials are used in terms of functionality, load capacity, production and costs, in order to save resources and reduce environmental pollution [8]. The properties of a clinched joint in strength testing are characterized by strength, stiffness and energy absorption [2]. The most commonly used tests are the head tension test, the shear test and the peel test [1]. Typical failure modes are unbuttoning, neck fracture or a combination of the two [4]. The joint properties depend on the main factors geometry, component properties and load type. The influence of the tool geometries on the clinching point has been investigated in many publications. The influence of variation of the mechanical properties of the joining partners and corresponding process parameters has been studied less. The influence of pre-stretching in preceding forming processes, which has an influence on the clinch joint [10], requires further studies. For example, 5 % pre-stretching can reduce the strength of the connection by 20 % and larger pre-stretches can lead to a failure of the clinched point in the joining process [11]. Material aging, especially with aluminum, also influences the material properties [10] and thus the joining process.

1.2.2 Pre-stretching for the joining partners

Pre-stretching or pre-strengthening can occur during the manufacturing process of the sheet metal or through preceding processes to clinching and can amount to 10 % to 15 % elongation in automotive engineering [12]. In general, work hardening during pre-stretching increases the strength of the material [13], thereby increasing the resistance to deformation [11] and reducing ductility [11] by adding ductile damage to the material [14]. Pre-stretching of the sheets before clinching leads to a reduction in joint strength or even to an insufficient joint due to cracking in the material during the joining process [11]. It is therefore necessary to select clinching tools and clinching parameters that can tolerate influences such as pre-stretching [11] before joining. The influence of pre-stretching can then be determined in material tests, such as the tensile test [15], or directly in the process, e.g. by clinching [11] the specimens. The pre-stretched specimens are often not available in the product development process [11], which means that the tool design must be carried out with the material in its delivery condition. However, pre-stretching can be applied in uniaxial tension [16] or biaxial tension [12]. Although the tensile tests do not reflect the real stresses and strains of a preceding forming process, it can be used to simulate an increase in strength and to introduce ductile damage [11]. However, pre-stretching can only be carried out up to the maximum homogeneous elongation at which no necking occurs [17] and thus depends on the elongation capacity of the selected material.

1.2.3 Finite element analysis

With finite element analysis (FEA), sensitivity analyses, technological optimization [8], creation of joining process windows [9] and parameter studies [18] are possible. Previous FEA investigations have mainly focused on the investigation of clinching parameters and basic mechanisms, such as tool geometries [19]. To reduce the calculation time, rotational symmetry [8] or the selection of one or more symmetry planes in 3D [20] can be used. The pure Coulomb friction model [21] or the Tresca friction model with modification by a shear limit [6] can be used, for which coefficients of friction between 0.0 [7] and 0.4 [22] are usually applied. Fine meshing is important due to the large local deformation [8]. Mesh sizes used in simulations with sufficient accuracy are reported between 0.05 mm [10] and 0.25 mm [8].

To determine the material data for the simulation, the multi-layer compression test, the uniaxial tensile test, the plane strain upsetting-test [8] and the bulge test [23] have been successfully applied in the literature. To interpret the material data in the simulation, a flow curve and a yield curve must be determind. The isotropic assumption must be used e.g. for 2D simulations [19], but can also be sufficient for 3D simulations in many cases [24]. The extrapolation of the yield curve can be done e.g. with the Swift model [25], the Voce model [26], the Hollomon model [10] or the Cowper-Symonds model [27]. The Swift and Voce model are the most commonly used in the more recent publications.

To ensure the accuracy of the FE-model, a mesh study, a parametric study of the contact conditions [28], a study of the friction coefficients [29] and a check and adaption of the material modeling for the simulation of a clinching process is necessary [23]. The geometry of the joint can be considered for evaluation and calibration [29] until an acceptable deviation from the real experiment is achieved [28]. In [30] the influence of strain hardening and the variation of sheet thickness on the joint characteristics \(t_{{\mathrm {n}}}\), f and \(t_{\mathrm {b}}\) are studied using a metamodel to investigate the robustness of the clinching process. In [31] the possibilities and limitations of FEM-based sensitivity analysis and optimization for the clinching process are discussed. For the optimization of the clinching tools, the sensitivities of the most important tool dimensions and a robustness analysis are determined. For exact simulations, it is recommended to consider the damage development [28]. Without the inclusion of damage, the simulation is less accurate and may not be able to determine the correct failure mode and overestimate the loading capacity [6]. According to [7], however, there are still relatively few FEA studies on the relationship between tool geometry and process-induced defects. Damage models that have been used for clinching simulations include Oyane [7], Cockroft-Latham [9], Rice and Tracey’s [7], Rousselier [7], Lemaitre [6] and Gurson-Tvergaard-Needleman damage model [2].

1.2.4 Design of experiments

For the investigation of numerous influencing variables and parameters, the use of a design of experiments (DoE) is useful [22]. In case of numerous experiments or long experimental time, it is reasonable to reduce the number of experiments via a DoE. A suitable experimental design must be selected to conduct the experiments and evaluation methods for the results must be determind. For the study of the clinching process, Taguchi’s DoE has proven useful for different influencing factors and has been used for observing the effects of tool geometry on clinching point geometries. In [28], Taguchi’s method is named as effective for studying influences of individual factors on quality characteristics and for optimizing product and process designs. The reduction in experimental effort was achieved by using an orthogonal array to consider all parameter combinations [22]. An orthogonal array is the smallest possible matrix of parameter combinations in which all parameters are varied at the same time [32]. Thereby, the orthogonal array can still be used to reproduce the complete information about the factors [33]. Thus, the study of the complete parameter space is possible with a few experiments [32]. It is necessary to choose an orthogonal array according to the number of factors and factor levels. It is useful to use at least three factor levels, with the middle factor level being the central point of the parameter [33]. The experimental design only provides the basis for considering all effects and interactions [2]. For the evaluation of the effects and interactions, the calculation of the average effect [32] of each parameter, the main effects, a range analysis, the analysis of variance ANOVA [34] and the signal-response relationship of the parameters to the results [33] are possible.

2 Materials and methods

FEA and experimental investigations are carried out to investigate the interaction between the joint and component properties during clinching. A dual-phase steel HCT590x with sheet thicknesses of 1.00 mm and 1.51 mm is used for the investigations. The material properties for the FEA are determined by uniaxial tensile tests. Material and tool data are then used to set up the simulation and the subsequent calibration. For validating the simulation results, specimens are pre-stretched in the tensile test to achieve work hardening and ductile damage to the specimens for clinching. Secondary specimens are then taken from the pre-strained specimens. A Taguchi experimental design is applied to perform the sensitivity analysis. For the experimental confirmation of the results, the geometric cross-section and the strength of the joint are used as criteria.

2.1 Clinching

2.1.1 Experimental set-up

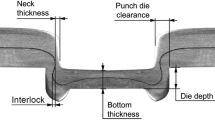
The investigation of the clinching process for the selected materials and sheet thicknesses requires the determination of suitable clinching tool combinations to produce a joint with sufficient neck thickness \(t_{\mathrm {n}}\) and interlock f without failure caused by material damage. Only closed dies with a joint diameter of 8 mm and conical punches are used. The conical punch relieves the neck area of the die-side sheet, which is relevant for the strength of the joint. However, it decreases f. However, a sufficient f is still achievable with a suitable parameter set and tool. The resulting bottom thickness \(t_\mathrm {b}\) was used as the primary criterion for the tool selection. With a \(t_\mathrm {b}\) lower than 25 % of the thickness of the sheets, the strength decreases and the risk of damage increases. With \(t_\mathrm {b}\) greater than 60 % of the thickness, there is no mechanical closure due to an insufficient formation of f. The bottom thickness can only be reduced with a given tool until the die is completely filled. A further reduction can cause the sheets to lift off the die or lead to punch fracture. The bottom thickness \(t_\mathrm {b}\) depends on the displaced volume by the punch and thus on the punch diameter. Therefore, with a larger punch diameter, the minimum possible \(t_\mathrm {b}\) increases, but with a smaller diameter the formation of f is reduced. Different punch and die combinations are tested for the different sheet thicknesses and the final tool selection is based on cross-section analysis regarding \(t_{\mathrm {n}}\) and f.

A position-controlled pneumohydraulic drive from TOX with a maximum joining force of 100 kN is used to produce the clinched joints. A spring with a spring rate of 628 N/mm is used for the blank holder. With the 4.7 mm pre-load stroke, this results in a blank holder force of approx. 3 kN. The die BD8016 and the punches AC62100 and AC52100 are selected as preferred variants, because a bottom thickness of more than 25 % and an f greater than 0.1 mm are achieved. The die BD8016 has a diameter of 8.0 mm and a depth of 1.6 mm. The conical punch AC62100 has a diameter of 6.2 mm and AC52100 has a diameter of 5.2 mm. The interlock f, the neck thickness \(t_{\mathrm {n}}\) and the achievable bottom thickness \(t_\mathrm {b}\) of the preferred variants are listed in Table 1. The chosen variant does not necessarily lead to the highest joint strength. Since a high strength material is used, a smaller f, which is associated with a greater \(t_{\mathrm {n}}\), can technically achieve a higher strength. However, the preferred variant is used for further testing, because of its greater sensitivity to parameter changes that are to be investigated here.

Table 1 Quality parameters of the clinching point for the selected tool combinations
Full size table

Since the influence of pre-strains on clinched joint quality is to be investigated virtually and as well as experimentally, the tool variants are tested in combination with pre-stretched material (Chapter 2.3). The 1 mm sheets can be joined up to an uniaxial pre-strain of 7.5 %. At a pre-strain of 10 % of the 1 mm sheets, cracks appear at the neck. Joining of the 1.51 mm sheets is possible with a pre-strain of 10 % without defects.The 1.00 mm sheet has a greater elongation at fracture compared to the 1.51 mm sheet. This leads to greater safety against damage and fractures.

2.1.2 Numerical set-up

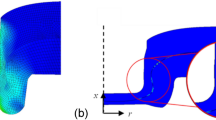
The procedure for building and calibrating the simulation is detailed in this chapter. A reference model is built and subsequently calibrated by adapting the material model and friction conditions using experimental data. For this purpose, the material model is calibrated first, which has a great influence on the beginning of the simulation and strongly affects the resulting neck thickness \(t_{\mathrm {n}}\) due to different yielding conditions. The numerical study of the clinching process are performed with SimuFact.Forming in 2D regarding influencing parameters like sheet thickness variation, pre-strain, sheet arrangement and punch stroke length. The effects of the different parameters are studied using the geometric quality criteria of the clinching point, but it is also useful to consider material damage. The Cockroft-Latham damage model [35] is used for this purpose. In Cockroft-Latham damage, a damage value is calculated from the ratio of the maximum tensile stress and the equivalent stress and summed over the plastic strain [36]. When a critical damage value is reached, the damage is indicated. Therefore, the Cockroft-Latham model is well suited to reproduce damage due to predominantly tensile stresses. The model can be used to compare different parameter sets regarding damage evolution. The dimensions of tools and sheets and their arrangement in the FE-model are shown in Fig. 1. In the model, the sheet thickness t and the corresponding punch diameter D are dependent on the sheet thickness.

Fig. 1
figure 1

Numerical set-up for the simulation of the clinching process. a Clinching tool geometry, b 2D axisymmetric FE-model of the clinching process with highlighted remeshing zone, c Detailed view of the remeshing zone with two refinement boxes

Full size image

The spring of the blank holder is modeled with a spring rate of 628 N/mm and a preload force of 3 kN. To achieve the required bottom thickness in the simulation, the penetration depth of the punch has to be adjusted. A mesh refinement box is defined for both sheets in the area of large deformations. The coarse meshing in the remaining areas saves computing time and is sufficient for accurate results as tested with a meshing study.

The dual-phase steel HCT590x in 1.00 mm and 1.51 mm sheet thicknesses is characterized in uniaxial tensile tests. For the tensile tests, the specimen geometry DIN 50125 - H 12.5 x 50 is used. The tensile tests are performed on a universal testing machine (Inspekt 250, Hegewald & Peschke) in combination with a GOM ARAMIS system using Digital Image Correlation (DIC). The results from tensile tests shown that the stress-strain curves of the 1.00 mm and 1.51 mm thick sheets differ greatly in the range up to 8 % strain and are almost the same thereafter. The 1.00 mm sheets have lower strength up to 8 % strain, which leads to the material yielding sooner.

Due to the large strains during clinching, a suitable extrapolation method is crucial for reliable results. For this purpose, different ranges can be chosen which are within the uniform strain. Swift, Voce and Hockett-Sherby are considered as possible yield curve models. Furthermore, the yield curves can also be adapted over the range of parameter determination. The Hockett-Sherby yield curve model with a fitting range between 10 – 15 % elongation provides the best results for the 1.51 mm sheet thickness. For the 1 mm sheet thickness, the best fitting of the yield curve is achieved with the Voce yield curve model and the fitting range between 10 - 15 %. The method of least squares was used for the fitting of the yield curves and the determination of the parameters for the models.

For model calibration, a mesh analysis is carried out first. Then the material model must be calibrated. This influences the start of the clinching process and controls the neck thickness through the material strength. Friction influences the force-displacement curve and the creation of interlock [37] and is calibrated last.

First, the workpieces are meshed as in Fig. 1. For this purpose, an initial mesh size is defined with a mesh refinement box for larger deformations. Local mesh sizes from 0.20 mm to 0.012 mm are tested in the relevant area for the clinch point formation. In general, the different meshing only has a slight influence on the geometric cross-section parameters. However, a greater accuracy due to finer meshing leads to an increased accuracy of the calculated plastic strain. The difference in finer meshing is most visible in the neck region of the upper sheet at the upper surface. Based on the investigation, a mesh size of 0.10 mm is used for the simulations. The mesh size in the refinement box for the upper sheet is 0.025 mm and for the lower sheet 0.05 mm.

For the study on friction, different friction coefficients are assumed for the two contact areas: tool-workpiece and workpiece-workpiece. The neck thickness \(t_{\mathrm {n}}\), the interlock f and the punch force are evaluated. Based on this analysis, a value of 0.02 is assumed for the friction between workpiece and tool and 0.2 for the friction between workpiece and tool for the 1.00 mm sheets. For the 1.51 mm sheets, a coefficient of friction of 0.1 is assumed for the friction between the workpiece and the tool, and 0.3 for the friction between the workpiece and the tool. The different friction coefficients are likely caused by different surface conditions of the sheets. The 1.00 mm sheets have a lower surface roughness than the 1.51 mm sheets. The comparison of the cross-sections from the experiment and the simulation for the calibrated models is shown in Fig. 2. When comparing the cross-sections, the characteristic course of the parting line between the two sheets can be reproduced well for both sheet thicknesses. The simulation results generally show very good agreement with the experimental results.

Fig. 2
figure 2

Comparison of cross-section geometry experiment and 2D simulation a 1.00  mm and b 1.51  mm

Full size image

The geometric quality characteristics can also be reproduced with sufficient accuracy. These are compared in Table 2.

Table 2 Comparison of the geometric properties neck thickness \(t_{\mathrm {n}}\) and interlock f from the simulation and the experimental test
Full size table

The deviations of the simulations from the real experiment are sufficiently small. In the neck area, the deviation is less than 10 %, which corresponds to a good accuracy when taking into account the many simplifications made. For the interlock f, especially for the 1.51 mm sheets, the deviation is larger, but still acceptable. The deviation of the bottom thickness \(t_\mathrm {b}\) is partly due to the deviation of the neck thickness \(t_{\mathrm {n}}\). The error of the deviated \(t_{\mathrm {n}}\) affects the f more than the \(t_{\mathrm {n}}\) itself. With a larger \(t_{\mathrm {n}}\), the f would also become smaller and more accurate. Possible causes for the deviations are the extrapolated material model, the assumed constant Coulomb friction conditions and the simplified 2D model.

2.2 Pre-stretching of the material

Uniaxial tensile tests are used to investigate the influence of material pre-strain on the clinching process. The uniaxial tensile test has the advantage that only a negligible change in material thickness occurs. To achieve uniform strain, the dimensions of the specimen are designed according to DIN 50125. It should be noted, that secondary specimens must be taken at \(0^{\circ }, 45^{\circ }\) and \(90^{\circ }\) from the uniformly elongated area. The dimensions of the specimen for pre-stretching can be seen in Fig. 3. It has a uniformly stretchable length of 65 mm for 1 mm sheets and 50 mm for the 1.51 mm sheets.

Fig. 3
figure 3

Secondary sampling from pre-stretched specimen: tensile test specimen at a \(0^{\circ }\), b \(90^{\circ }\) and c \(45^{\circ }\) to rolling direction and d shear test specimen

Full size image

The secondary sampling from the pre-streched specimen is shown in Fig. 3. The geometry of the modified tensile specimen DIN 50125 E 1 x 6 x 20 and DIN 50125 E 1.51 x 6 x 20 and a shear tensile specimen with the dimensions 45 mm x 105 mm are used. The pre-stretching is performed at a uniform speed of 2 mm/min. The pre-strain is recorded in the area of uniform strain from which the secondary specimens are to be taken. Specimens with 5 %, 7.5 % and 10 % pre-strain are produced.

2.3 Numerical sensitivity analysis of the clinching process

A numerical sensitivity analysis using FEA is carried out on the interactions between the joint geometry and component properties and their relevant influencing factors. The sensitivity analysis shows the effects of the selected parameters on the clinching point quality. To reduce the experimental effort and to enable the evaluation of more result variables, such as ductile damage and material flow, the analysis is performed using a Design of Experiments approach (DOE). The parameters initial sheet thickness, pre-stretching of the material, sheet arrangement and variation of the bottom thickness are to be considered, see Table 3. The strain levels are selected to ensure that a shear specimen can be taken from the tensile specimen for pre-stretching while maintaining a uniform strain level in the overlap area of the shear specimen. A change in the initial yield stress is considered via the pre-stretching of the material.

Table 3 Parameters and levels for the sensitivity analysis
Full size table

Three parameter levels are selected, so that non-linear effects can also be detected. For the second parameter level, a sheet thickness 1.25 mm is added. For the 1.25 mm sheet metal, a punch with a diameter of 5.8 mm is used. For the study, the experimental design L9 according to Taguchi is selected as it is suitable for four parameters with three parameter levels. Since Taguchi L9 has the capability of a full factorial experimental design, all interdepencies between parameters can be detected and analysed. For a full factorial analysis, four parameters with three parameter levels have \(3^4 = 81\) combinations. With the Taguchi L9, see Table  4, only nine simulations with certain parameter combinations are necessary to reproduce all effects.

Table 4 Design of experiments according to Taguchi L9
Full size table

3 Results

3.1 Investigation of process sensitivities using the Taguchi experimental design

For the evaluation of the simulations, the interlock f, the neck thickness \(t_{\mathrm {n}}\), the maximum force and the damage in the neck and in the bottom of the clinch point are considered. For better illustration, the effects of the individual parameter levels are shown in comparison to the overall effect in Fig. 4. The average effect is calculated by dividing the sum of all result variables of a result by the number of results, see equation (1) [19].

$$\begin{aligned} \overline{\mathrm {Result_{X}}} = \frac{\sum \mathrm {Result_X}}{9} \end{aligned}$$
(1)

The average effect of a parameter \(\overline{y(A_k)}\) is calculated using the equation (2) [19]. A is the parameter, k the factor level and r the number.

$$\begin{aligned} \overline{y(A_k)} = \frac{\sum _{1\le i \le r(A_k)}y_i A_k}{r(A_k)} \end{aligned}$$
(2)

Thus, the results of a factor level are summed up and divided by the number of results obtained with this factor level. The results of the average effects of the parameters compared to the total average effect of all parameters are shown in Fig. 4.

Fig. 4
figure 4

Results of the average effects of the parameters

Full size image

The main effect on the neck thickness \(t_{\mathrm {n}}\) is the sheet thickness, see Fig. 4 a). As the sheet thickness increases, the \(t_{\mathrm {n}}\) increases. Pre-stretching also has a non-negligible effect on the \(t_{\mathrm {n}}\), because it reduces it. The influence of the pre-stretching on the \(t_{\mathrm {n}}\) also depends on the arrangement.The effects on the interlock f are shown in Fig. 4 b). The main effects are the sheet thickness and the bottom thickness, which results from the punch stroke. While the interlock increases approx. linearly with punch travel, the sheet thickness has a non-linear effect, with the thicker sheets producing the largest f. A linearity can also be seen with the effect of pre-strain. f increases with pre-strain. Also for f, the effect of the pre-stretching depends on the arrangement of the sheets. The influence of the parameters on the maximum joining force during clinching is shown in Fig. 4 c). The penetration depth has the greatest influence on the joining force, with the maximum force increasing almost linearly with increasing punch stroke. The other parameters have a comparatively small influence. With greater sheet thickness, the joining force becomes smaller, and with greater pre-stretching, the joining force becomes higher. The reduction in the joining force with greater sheet thickness is due to the punch diameter. A larger punch diameter is used for thinner sheets. This means that more material is compressed in the final phase of the clinching process. In this case, the force to form the workpiece is greater, but the frictional force is also greater because of the larger surface area.

The effects of the parameters on the material damage, expressed by the Cockroft-Latham damage, on the neck region of the punch-side sheet and the bottom of the die-side sheet are shown in Fig. 4 d). In the neck area, all parameters have a great influence. With thinner sheets, larger pre-strain and larger punch stroke, the damage in the neck region increases significantly. All parameters have a recognizable effect on the damage in the bottom area. With greater sheet thickness, pre-stretching and punch penetration depth, the damage in the bottom increases significantly. Generally, thinner sheets are more sensitive to parameter variations. This is evident e.g. in the Cockroft-Latham damage. The damage during the simulation with the reference process is shown in Fig. 5.

Fig. 5
figure 5

Comparison of Cockroft-Latham damage for a 1.00  mm and b 1.51  mm sheets

Full size image

For thinner sheets, the damage is higher in the neck area and for thicker sheets at the bottom. Since the 1.00 mm sheets have lower degrees of deformation, but higher damage in the neck area, it can be concluded that thin sheets are more susceptible to damage in the neck area due to the geometric conditions. In the bottom area, the thicker sheets are more susceptible. This is mainly due to the greater deformation in this area.

Fig. 6 compares the clinching of the 1.51 mm sheets without pre-stretching and with 5 % pre-stretching on the punch side. It is clear that with the pre-stretched combination the damage in the neck has increased, purely from the clinching process and without the damage from the pre-stretching. Furthermore, it is visible that the neck thickness is reduced. This is due to less material being pulled into the die due to the higher yield strength of the pre-strained material. This result and the result from Fig. 5 indicate that the increase in damage in the neck area has a geometric cause.

Fig. 6
figure 6

Comparison of Cockroft-Latham damage and neck thickness of the 1.51  mm sheets at a 0 % pre-stretching and b 5 % pre-stretching

Full size image

This extensive numerical study shows that all four investigated parameters sheet thickness, pre-strengthening, sheet arrangement and positioning error of the punch have a clear influence on the formation of the clinching point. However, the results still need to be confirmed by experimental tests. The effects of the parameters on the geometric and damage properties of the clinching point must be considered, but more importantly on the strength of the clinched joint as a derived quantity from these geometric and material parameters.

3.2 Influence of pre-stretching on clinching point properties

Using the simulations of the clinching process, information on the effects of pre-stretching of the materials could be obtained. However, these must be matched with selected experiments to verify the results of the simulations. The experimental investigations are mainly focused on the pre-stretching, which can have an influence on the geometry and the damage status according to the FEA investigations. Therefore, specimen with 0 %, 5 %, 7.5 % and 10 % pre-stretching are clinched for further tests using the reference tools from Chapter 2.2 and evaluated using cross-section micrographs. During the clinching process, it was noticeable that the same bottom thickness could not be achieved with pre-stretched specimens compared to unstrained ones. The reason for this is an increased yield strength, which inhibits the material flow and prevents the complete filling of the die. Nevertheless, the results at the clinch points for pre-stretched material specimens confirmed the results of the simulation.

Table 5 shows that with higher pre-strain, the neck thickness \(t_{\mathrm {n}}\) of the clinching point is smaller. This is consistent with the results from the numerical pre-strain sensitivity analysis, where the higher yield strength also causes a reduced material flow into the die so that \(t_{\mathrm {n}}\) of the punch-side sheet becomes smaller. Thus, this experiment has confirmed the change of the geometric quality parameters of the clinching point due to pre-strained sheets while also validating the numerical analysis.

Table 5 Pre-stretching geometric data of the clinching points
Full size table

Furthermore, this test also confirmed that pre-stretching can lead to failure of the clinch point and that thin sheets are more sensitive to this influence than thick sheets. At 10 % pre-strain, the 1.00 mm sheets failed by neck breakage on the punch side. For the 1.51 mm sheets, clinching was possible without failure even with 10 % pre-strain. The failure is due to the increased ductile damage resulting from the pre-strain and from the changed clinching process compared to unstrained materials. The shear tensile test of the clinched specimen is suitable for determining the static strength of the clinching point under shear stress. The specimen geometry, test arrangement and test procedure are designed according to DVS/EFB 3480 [38]. A testing speed of 5 mm/min is applied. The punch side plate is prepared by secondary sampling from 0 %, 5 % and 7.5 % pre-strained specimens. Five specimens are tested for each parameter set.

The results of the shear tensile test are shown in Fig. 7 with the mean values of the force-displacement curves. In the shear tensile tests of the 1.51 mm specimens, strengths between 4.64 kN and 4.98 kN are achieved. Furthermore, it can be seen from the force-displacement curves that with 5 % and 7.5 % pre-stretching the joint fails at a lower displacement and that 7.5 % pre-strain leads to weakening by about 0.34 kN of the joint strength. In the shear tensile tests of the 1.00 mm specimens, strengths between 3.58 kN and 3.75 kN are reached. While the joint strength is basically the same over all samples, the displacement until failure differs significantly depending on existing pre-strain. This suggests that changes occurred regarding the failure mode or at failure with the failure mode remaining the same.

Fig. 7
figure 7

Force-displacement curves for shear test with material pre-stretched on the punch side

Full size image

The separated clinched joints due to failure in shear tension of the 1.51 mm sheets are shown in Fig. 8. In all shear tensile tests, including both 1.00 mm sheets, a combined failure by unbuttoning with neck breakage occurred. Fig. 8 shows that the investigated clinched joints fail differently depending on varying pre-stretching, but maintain the same failure mode. The investigations have shown that the pre-strain reduces the shear tensile strength and affects the failure behavior of clinched joints. This confirms the results of the simulation, as the larger ductile damage leads to the reduction of the shear strength, but also the reduced neck thickness.

Fig. 8
figure 8

Failed connection after shear test of the 1.51 mm sheets at a 0 %, b 5 % and c 7.5 % pre-stretching

Full size image

4 Conclusion

Based on the performed numerical and experimental investigations it is shown that for the investigated materials a correlation exists between the influences on the material by preceding processes and the properties of a clinched joint. The parameters initial sheet thickness, pre-stretching of the material, sheet arrangement and variation of the bottom thickness are considered for numerical investigations. For the evaluation of the simulations, the under-cut, the neck thickness, the maximum force and the damage in the neck and in the bottom of the clinching point are analysed. For example, it is demonstrated that thinner sheets are more sensitive to damage during clinching than thicker sheets. The parameter influences can be well reproduced by FEA, which reduces the experimental effort and makes it possible to consider the damage in the clinched joint. This can shorten development times, reduce costs due to errors and improve the quality of clinched connections. In addition, experimental studies were carried out to investigate the influence of pre-stretching of the sheets on the geometry and strength of the clinching point. It is observed that pre-stretching of the workpieces influences the characteristic geometry and the strength of clinching point. This is an important finding for the application of clinched joints in complex sheet structures, since in most cases the joined components will have undergone different forming processes subjecting them to varying degrees of pre-strain and material damage before clinching. These effects cannot be neglected if clinched joints are to be used to their full load bearing capacity without high safety factors leading to oversizing and consequently waste of resources.