Abstract
The increasing demands for the reduction of carbon dioxide emission require intensified efforts to increase resource efficiency. Especially in the mobility sector with large moving masses, resource savings can contribute enormously to the reduction of emissions. One possibility is to reduce the weight of the vehicles by using lightweight technologies. A frequently used method is the implementation of multi-material systems. These consist of dissimilar materials such as steel, aluminium or plastics. In the production of these systems, the joining of the different materials and geometries is a central challenge. Due to the increasing demands on the joints, the challenges for the joining processes itself are also increasing. Since conventional joining processes are rather rigid and can only react to a limited extent to disturbance variables or changing process variables, new methods and technologies are required. A widely used conventional joining method with these properties is self-piercing riveting. Because of the rigid tool combination and the fact that the rivet geometry that can be used is related to the tools, the joining of multi-material systems requires tool and rivet changes during the process. In order to extend the process window of joining with self-piercing rivet elements, the process is enhanced with a tumbling kinematic of the punch. The integration of tumbling results in a significant increase in the adjustable process parameters. This enables a higher material flow control in the joining process through a specific tumbling strategy. The materials investigated are a steel and an aluminium alloy, which differ significantly in their mechanical properties and have many applications in automotive engineering, especially for structural car body components. The steel material is a galvanized HCT590X+Z dual-phase steel, which is characterised by a low yield strength, combined with high tensile strength and a good hardening behaviour. The aluminium alloy is an EN AW-6014. The precipitation-hardening alloy consists of aluminium, magnesium and silicon with a high strength and energy absorption capability. The objective of this work is to obtain a fundamental knowledge of the new tumbling self-piercing riveting process. With different mechanical properties and different sheet thicknesses of the joining partners, the influences of these parameters on the tumbling strategy of the riveting process are analysed. Such a tumbling strategy is based on the tumbling angle, the tumbling onset and the tumbling kinematics. These parameters are investigated in the context of the work for selected combinations of multi-material systems consisting of HCT590X+Z and EN AW-6014. With the variation of the parameters, the versatility of the process can be investigated and influences of the tumbling on the self-piercing riveting process can be identified. To illustrate the results, force–displacement curves from the joining process of the individual joints are compared and the geometry of the rivet undercut and rivet heads are geometrically measured. Furthermore, micrographs allow the analysis of the characteristic joint parameters interlock, residual sheet thickness and end position of the rivet head.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
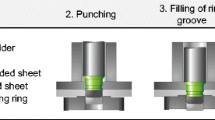
Several decisions have been taken by the European Union to reduce greenhouse gas emissions in order to prevent climate change [1]. The road traffic in the European Union contributes a large share of the emissions with almost 26% of the total CO2 emissions [2], therefore a regulation for the fleet consumption of passenger car manufacturers has been imposed in 2005 [3]. Various measures are being taken to achieve these targets, including reducing the weight of the moving masses in order to save energy and preserve resources [4]. One method of weight reduction is the application of lightweight constructions [5]. These assemblies consist of so-called multi-material systems, which are characterised by materials with different mechanical and geometrical properties and can thus be designed to suit specific requirements [6]. The different materials can be, for example, high strength steel and aluminium alloy sheets [7] and the geometrical properties can be characterised by varying sheet thicknesses and basic body geometries. However, there are a number of challenges to be considered in the manufacturing of lightweight constructions, including the joining technology used to produce the connections in multi-material systems [8]. The increasing requirements necessitate new technologies and processes, as conventional methods are reaching their limits. A well-known but comparatively rigid joining process is semi-tubular self-piercing riveting, which is shown schematically in Fig. 1. This technology is a mechanical joining process that is widely used in industry and is well known for joining assemblies [9]. However, the versatility of the process is significantly limited due to the rigid tools and the resulting complex sampling processes [10]. In order to be able to react to the described upcoming challenges, a further development of the process is necessary, which makes an increased control of the joining process possible.
Semi-tubular self-piercing riveting according to [11]
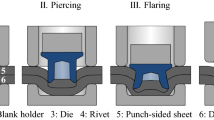
One possibility for further development and for increasing adaptability is to superimpose the semi-tubular self-piercing riveting process with a configurable tumbling process. The tumbling process is shown in Fig. 2 on the right and differs from the conventional upsetting process, shown on the left, by the reduced contact area [12] between the rivet head and the punch. Reducing the surface area and moving the contact surface on the workpiece in a targeted pattern makes it possible to control the material flow, as fundamental studies on tumbling have shown [13]. Tumbling originally derives from bulk metal forming, but has also been used, for example, in sheet bulk metal forming to provide material locally and to take advantage of the ability to control the material flow from the process. In a tumbling process, the tumbling strategy consists of several components. Important parameters that can be set are the tumbling angle, the tumbling kinematics, the tumbling speed and the tumbling onset [14]. Investigations on the influence of the tumbling angle were carried out in [15], which showed that an increased tumbling angle significantly reduces the required forming force level compared to conventionally compressed workpieces. However, in [15] it is shown that this effect of decreasing force level is only significant up to a tumbling angle of 10° and then is progressively reduced.
In [16], investigations were carried out on a superposition of a semi-hollow self-piercing riveting process by a tumbling process. Conventional tumbling riveting tools were used, which utilised orbital and radial riveting processes. In the context of the investigations presented here, a versatile process combination is investigated. This requires a tool that can realise different tumbling kinematics with varying tumbling angles. The aim is to construct a versatile joining process that can react to variations regarding the sheet thickness and the mechanical properties of the joining partners. The structure of the process combination and the tool are presented subsequently.
2 Tool design
The combination of self-piercing riveting and tumbling is shown in Fig. 3. Instead of the conventional punch, a tumbling punch is integrated as described above, which can be identified, as the punch axis tilts out of the tool axis by the angle α. To investigate the fundamental scientific interrelationships of the process combination, a tool is constructed which is able to realise the process route.
The tool set up for investigating the versatility of the tumbling semi-tubular self-piercing riveting process is depicted in Fig. 4. In the centre of the figure, an overview of the entire tool is shown and in the detailed views on the left, the area of the joint manufacturing and on the right, the implementation of the tumbling kinematics can be seen. To conduct tests, the tool is installed in a universal testing machine from type Walter+Bai FS-300. This enables the punch to be moved and provides force and displacement data of the process. For the production of tumbling joined semi-tubular self-piercing rivet joints, all tool components are required that are also necessary for the production of conventional self-piercing rivet joints. The basic framework thus consists of a die, which is fixed in a die holder and can be exchanged in this tool. Additionally, the joining partners and the semi-tubular self-piercing rivet are placed on the installed die. To clamp the sheets in order to prevent them from bending up during the process, a blankholder is implemented. It is not possible to insert the rivet elements into the blankholder as in a conventional process, because a distance between blankholder and punch is required to tilt the punch axis out of the tool axis. Therefore, the rivet element has to be placed on the specimen manually with a positioning template. The blankholder is closed via two hydraulic cylinders and can be continuously applied with force. To investigate the influence of the blankholder on the joining process, the blankholder can be exchanged to adapt the contact surface between the punch-side sheet and the blankholder. To apply the joining force, a tumbling punch is used, which has a conical shape with β = 7° due to the maximum possible tumbling angle of the tool. It is possible to change the tumbling punch and investigate the influence of different punch geometries. The pillar guides shown in the figure ensure a precise positioning and guidance of the upper and lower tool components. To achieve the tumbling angle, in this tool concept the punch axis is tilted out of the tool axis. The punch is installed in the middle plate in a spherical bearing that has its pivot point outside and thus rotates around a fixed point located in the centre of the rivet head. This means that the centre of the punch is at a fixed point in the x–y plane of the tool. The adjustment of the tumbling angle is implemented with a combination of a rotating axis and a linear axis. The upper mounting point of the tumbling punch is also in a spherical bearing, however, it has its pivot point in the centre of the bearing. By combining two spherical bearings, the load path can be divided and the force level for the adjusting mechanism of the punch can be reduced. When moving the punch, only the frictional torque between the punch and the riveting element has to be overcome by the tool and not the entire punch force must be transmitted. The bearing of the punch is mounted on a linear guide, which is fixed on a rotatable plate. This enables both rotating and linear movements to be realised.
This combination was chosen because it allows different kinematics to be dynamically executed with predominantly linear as well as rotating movements. The rotational axis is driven by a belt and can be positioned with high precision by the servo motor in combination with a planetary transmission. To avoid the necessity of rotary feedthroughs for the implementation of the kinematics, the linear axis is driven by a combination of pinion-gear rack, a shaft and a belt. The implementation of the mechanical kinematics is described in more detail below. Two laser triangulation sensors that measure the distance to the punch at a defined point are installed to monitor the resulting angle of the punch. Additionally, the laser sensors are used to prevent a crash of the tool by controlling the maximum deviation of the tool axis to the punch axis. Since in a tumbling process a torque occurs because of the contact between punch and rivet but no rotation of the punch is accepted, a rotational limiter is necessary. The limiter prevents an undefined rotation of the punch around the z-axis, but allows a rotation in the pivot point around the x- and y-axis. The belts are driven by a transmission unit with electric motors. The drives are controlled via servo systems and a Programmable Logic Controller (PLC) from the Beckhoff company in which all kinematic models to investigate different tumbling strategies are defined. The precise interpolation of the axes is done by the PLC and only the positions of the axes depending on the kinematics have to be specified. This makes it possible to programme the movement of the tumbling punch completely unrestricted and to allow a fundamental investigation of the influence of the kinematics and the tumbling angle. The control system of the tool is able to access the force and displacement data of the testing machine with analogue inputs, ensuring an independence of an operator influence concerning the specified tumbling onset. A master and two slave axes are defined in the control unit, which serve as the basic coordinate system for the tumbling kinematics. The master axis is a virtual axis and the two slave axes are assigned to the physical axes. The master axis can be used to set cross-process parameters such as the tumbling speed, while the slave axes are used to implement the kinematics. The tool details relevant for the investigations are shown in Table 1.
Figure 5 shows a schematic illustration of the implementation for moving the tumbling punch with a circle kinematic shown as red line. In the perspective view (a), the line represents the path of the upper spherical bearing. In the view (b) of the x–y plane of the tool as a cross-section through the rotational and linear axis from Fig. 4, the functionality of setting the tumbling angle is explained. The basis of the system is a combination of a rotational and a linear axis. This combination enables both linear and rotating tumbling kinematics with high dynamics. The motor 1 drives the rotational axis with a belt, which causes the rotation of the rotation plate. On the rotation plate, a linear bearing is mounted on which a carriage moves. A rack is mounted on this carriage and by using a pinion, a movement along an axis can be realised via the rack and the linear guide. The pinion is driven by the motor 2 of the tool. As a result of the two axes, any point on the rotation plate can be reached and thus a completely free movement of the punch is possible. For the movement of the punch with high dynamics, a synchronisation of the two axes is necessary, since a crash of the tool occurs when the axes move asynchronously. The tumbling angle of the punch is realised by an angular offset between the two axes. If the speed of the two axes differs, a translational movement occurs in addition to a rotating movement due to the increasing angular offset between the two axes. Thus, the angle can be adjusted and kept constant with equal angular velocities of the axes. When the angular difference between the two axes is at a maximum, the tumbling angle is at a maximum as well.
3 Methods and procedure
The presented tool can be used for different investigations. Within the scope of this work, the influence of several parameters on the process combination consisting of tumbling and self-piercing riveting is investigated. Two materials are used to represent multi-material systems, which have many and different fields of application in the automotive industry. The steel material chosen is a dual-phase steel HCT590X+Z with an initial sheet thickness of 0.8 mm and a zinc coating. The joining partner is a precipitation-hardenable aluminium alloy EN AW-6014 consisting of aluminium, silicon and magnesium with an initial sheet thickness of 2.0 mm. The two materials have fundamentally different mechanical properties. The yield strength of the steel is approximately 410 MPa, whereas the aluminium has a yield strength of approximately 140 MPa. The tensile strengths also differ and are about 680 MPa for the steel and about 245 MPa for the aluminium alloy. The geometric properties also vary to a great extent and, with initial sheet thicknesses of 0.8 mm and 2.0 mm, have a difference of 1.2 mm. To compare the joint quality and to identify transferabilities, joint properties of connections with a mono-material pairing consisting of 1.5 mm aluminium sheets with the same base material are referred. Another important influencing component on the presented process is the tumbling kinematics. This can have a considerable influence on the resulting riveted joint due to different speeds and trajectories. To investigate this parameter, two kinematic models are selected, consisting of circular and spiral kinematics, shown in Fig. 6a. The left side shows a circular kinematics, which is characterised by the fact that the tumbling angle is first approached with the number of rotations UU of rounds to build up the maximum tumbling angle, as shown in Fig. 6b. In the second phase of the circular kinematics, the tumbling angle is kept constant over the number of revolutions UC. In the investigations shown, the angle is built up during one revolution and then kept constant until the punch reaches a target stroke. This means that for UC no number can be specified, since this value depends on the punch stroke.
The spiral kinematic is different in the sense that it is built up over the entire joining process and the tumbling angle continuously increases. From this it can be concluded that the maximum tumbling angle is reached at the end of the joining process and that the tumbling angle increases more homogeneously than with a circular kinematic. The variable UU is not specified for both kinematic models, but derives from the three parameters of the maximum punch stroke, the tumbling speed and the tumbling onset. The steady increase of the tumbling angle can be taken from Fig. 6b, which shows a constant incline of the graph. The speed of the tumbling kinematics is defined by a master axis as described above. In the case of spiral and circular kinematics, the master axis is equal to the rotational axis of the tool. Thus, the tumbling speed for the axis of rotation can be set to ω = 100°/s. This value is chosen because a stable process can be realised and the tumbling kinematics as well as the joining process can be reliably controlled. The tumbling speed is directly related to the speed of the punch. The z-stroke of the punch is caused by the traverse of the universal testing machine. The proportion between the crosshead speed and the tumbling speed must be in a range where neither of them predominates the process. The crosshead speed is set to vT = 10 mm/min, thus with the spiral and circular kinematics 0.6 mm stroke of the punch is realised for one complete revolution of the tumbling punch. The total number of tumbling revolutions for a joining process also depends on the tumbling onset, since a later starting point at constant tumbling speed reduces the total number.
At the start of the process, the punch is driven at 2 mm/min to a pre-load of 100 N. The force rises as soon as the punch is in contact with the rivet. When the pre-load is reached, the testing begins and the universal testing machine accelerates to the required testing speed. In addition to the force that is introduced into the process by the tumbling punch, a blankholder is also required. For the blankholder, force values from literature are chosen according to [17]. The chosen blankholder force is FB = 5 kN for the sheet thickness combinations and materials investigated. For the aluminium-aluminium joints Rivset C 5.3 × 5.0 rivets and for the steel-aluminium joints Rivset C 5.3 × 4.5 rivets are used, both from Böllhoff company. The difference between the two rivet types is the height of the rivet, which is chosen lower or higher due to the varying total thickness of the two joining partners. The rivet elements were identified on the basis of sampling tests, which showed a good geometrical joint quality. Another component of the sampling is the selection of the die. A flat die type 090 2016 is used for both material pairings. To evaluate the joint quality, different parameters are varied. In Table 2 the tumbling strategy configurations of the investigated joint combinations are shown. First, the force–displacement data of the setting processes are recorded and examined. Furthermore, geometric dimensions of the joint are analysed. For this purpose, micrographs of the joints are prepared and measured.
The geometric joint parameters shown in Fig. 7 are measured and compared with each other. In addition to the conventional parameters of semi-tubular self-piercing riveting joints rivet head end position, undercut, and residual bottom thickness, which represent characteristic joint parameters used for the evaluation of the joint formation, the parameter of the rivet shaft thickness is added as a parameter. Investigations have shown that a thickening of the shank can occur due to tumbling and therefore the characteristic is quantified.
All values are measured on the right and left side in the micrograph, because the tumbling of the punch does not result in an axisymmetrical riveted joint. Furthermore, the samples are analysed non-destructively by optical 3D measurements. This allows insights into the three-dimensional position of the rivet heads caused by the tumbling punch. For these measurements, an optical 3D measurement system Alicona Infinitefocus G5 with 5× optical magnification is used.
4 Results
To identify differences between mono-material and multi-material joints, a steel-aluminium joint and an aluminium-aluminium joint are examined. The joining partners of the all-aluminium joint have the same initial sheet thickness of 1.5 mm, whereas the multi-material joints consist of 0.8 mm steel and 2.0 mm aluminium sheets, which are joined according to the hard in soft principle. Thus, the influence of equal and varying sheet thicknesses and materials on the joining process can be investigated. Materials with different mechanical properties were deliberately selected to represent the characteristics of multi-material systems. First, the average force–displacement curves of three tests of the joining processes for both material pairings with different tumbling angles shown in Fig. 8 are analysed. Other components of the tumbling strategy are the circular kinematics of the punch and the tumbling onset at hp = 3 mm. The different maximum punch strokes can be explained by the varying total thicknesses of the joining partners and the different rivet element heights.
In the first process section, the cutting of the two joining partners on the punch side, significant differences between the two material pairings can be detected. The multi-material combination with the steel on the punch side shows a clear cutting impact, which is characterised by a strong drop in force at hp = 2 mm. This phenomenon is caused by the significantly higher tensile strength of the steel compared to the aluminium underneath. This effect cannot be seen for the mono-material joint. The increase in force at hp = 2.1 mm is due to a contact between the die-side joining partner and the die. In addition, a significantly higher force level can be identified with the multi-material joint, which is almost twice as high as with the mono-material joint. However, the force level to which the curve descends is in a very similar range to that of the aluminium-aluminium joint. From this point on, the rivet element comes into contact with the die-side joining partner and this is the same material with the same sheet thickness in both joining points. From the point after the cutting impact, the force–displacement curves for all examined tumbling angles are characterised by a very similar course. The increase in force in the multi-material is significantly stronger, since a steel material is used in the joint, and is approximately 30% higher at the tumbling onset. Due to the tumbling onset, the gradient decreases in each case and with larger tumbling angles, the absolute force level even declines compared to the conventional process with tumbling angle α = 0°. With circular kinematics, the tumbling angles are applied over one revolution and with the larger angles a higher translatory speed to the outer radius is necessary. This speed is proportionally much greater than the traverse speed and thus the drives of the tumbling kinematics take on more of the forming work, which leads to a drop in the force in the z-direction for α = 4° and α = 6°. The resulting maximum forces at the end of the process show clear reductions with increasing tumbling angle. The ratios in which the joining forces decrease are at a similar level for mono and multi-material joints, which indicates a transferability of the effects regardless of the material combination. For the tumbling angle α = 2°, a smaller reduction of the force level after the start of tumbling than for α = 4° and α = 6° can be identified. Additionally, the difference to conventionally with α = 0° joined joints decreases towards the end of the joining process, since a strong deformation of the rivet head, as shown in the following, largely eliminates the contact area reduction and the force. The tests show that the process combination presented is able to join both mono-material and multi-material systems.
As shown above, the influence of the tumbling angle has a great impact on the force–displacement curve of the joining process. In addition to the angle, the kinematic is an important component of the tumbling strategy and is varied between two models in the following for the multi-material joint with a steel and aluminum sheet as joining partners, shown in Fig. 9. The graph shows averaged force–displacement curves from three tests with the same parameters. Up to the tumbling onset at hp = 3 mm, no significant deviations can be observed. With the onset of tumbling, differences between the kinematic models and the angles occur. The higher the tumbling angle, the lower the force level at the tumbling punch, depending on the used kinematic. The reduction of the contact area, caused by the adjusted tumbling punch, lowers the required force level, as the surface pressure increases. The differences in the forming work between conventionally with α = 0° and tumbled joints are covered by the motors of the tumbling unit of the tool. For the two different kinematics, the investigations show that the circular movement leads to a greater reduction in the force level after the tumbling onset. The tumbling angle is set to the maximum value over one revolution, whereas with the spiral shape the angle is built up over the entire tumbling process and only reaches its maximum at the end of the process.
As a result, the force–displacement curves of the spirally tumbled joints are more homogeneous. At the end of the joining processes, the tests with the same maximum tumbling angles also reach an almost identical force level, as the kinematics converge themselves again. The experiments show that the spiral tumbling kinematic deviates less from the conventional process with α = 0° compared to the circular kinematic and only minor absolute force drops occur in the spiral process.
In Fig. 10, micrographs of the complete joints with varying kinematics, tumbling angles and with tumbling angle α = 0° as reference are shown. Using these images, information about the joint qualities can be obtained. In the micrographs of both kinematics and all angular steps, a tilting of the rivet to the right side can be identified. The micrographs are all aligned the identical way to show the same sections in relation to the tumbling kinematic. The tilting of the rivets in one direction is based on the kinematics of the punch. At the end of the process, the punch is in contact with the rivet head on the right-hand side, where it causes a deeper penetration of the rivet shaft into the die and the joining partners. Furthermore, a conical shape of the rivet head can be identified in the micrographs. Due to the conical punch shape, contact is initially made in the centre of the rivet. By moving the punch further, the rivet spreads out to a very small extent and the characteristic rivet head geometry is generated. Another geometric feature is the thickening of the rivet shaft. This is a pattern of imperfection, which is not known from conventionally joined semi-hollow self-piercing piercing riveting joints. At tumbling angles with α = 6°, cracks occur in the rivet shaft, independent of the kinematic models investigated here. In the spiral kinematics, seen in detail view X, the rivet shank is completely split off on the right side and in the circular kinematics, detail view Y, a crack can be seen running radially inwards from the outside of the rivet shank. The circular kinematics also show a crack in the development phase on the right side, which also arose radially on the outside of the shaft.
The reasons for the crack formation at larger tumbling angles can be manifold. Due to the higher angle, the applied surface pressure is higher and thus the load on the material is significant higher. Furthermore, the cyclic load due to the tumbling movement of the punch can cause the crack formation. Due to the local application of force on the rivet head, the opposite side of the rivet is pressed against the steel sheet at the level of the crack formation. The high mechanical strength of both the steel and the rivet can explain the cracking of the rivet. The basic material of the rivet, which is in a hardened state, can also influence this defect pattern. In addition, the contact between the rivet head and the tumbling punch introduces a torque into the rivet that a conventional riveting element is not designed for. Furthermore, a thickening of the rivet shaft can be seen in the area of the crack, which is caused by the incremental forming. Here, as can be seen in Fig. 11, there is a thickening of more than 30% compared to the original shaft thickness.
In Fig. 11, the geometric properties of the riveted joints for the characteristic features from Fig. 7 are shown as a bar chart for comparison between the angles and kinematics as well as the reference joint with tumbling angle α = 0°. From the measured values, a noticeable trend of an increasing shaft thickness with higher tumbling angle can be observed. For spiral kinematics a maximum increase of approx. 10% and for circular kinematics a maximum increase of approx. 32% can be recognised. The increased shank thickness of the circularly tumbled rivets can be explained by the longer applied maximum tumbling angle in the process. In addition, a circular kinematic causes a greater increase in shaft thickness with α = 6° and the differences between the right and left shaft sides are comparatively small.
The differences between right and left shaft for the circular kinematics with α = 2° and α = 4° can be explained by the beginning phase of the process. The comparatively fast adjusted angle causes a stronger tilting at the beginning of the tumbling and the larger the tumbling angle becomes, the more this effect is reduced. For the undercut, it is noted that this also increases with rising tumbling angle, as the rivet is driven deeper into the die. Furthermore, circularly tumbled joints tend to show higher undercuts, but at the same time also greater differences between right and left side, which results from the tilting of the rivet in the joint.
In addition to the rivet head end position, the alignment between the joining point and rivet axis is relevant for specific geometric parameters of the joining point quality. As a result of the angle offset of the rivet axis to the joint axis, the effect of the rivet head end position on the joint characteristics is superimposed. Since the undercut is measured perpendicular to the contact surface of the die-side joining partner with the die, a difference arises due to the rotation of the rivet by the previously described angular offset. Depending on the tumbling kinematics, the angular offset of the rivet end positions is different and thus the undercut is also influenced. For the variation of the undercut, which results in investigations with spiral kinematics, the decrease of the contact surface, depending on the angle on the rivet head of the tumbling punch, is an important factor. Due to the uniform decrease over one rotation, an uneven distribution of the contact surface on the rivet head occurs and thus causes an angular offset of the rivet to the joint axis.
For the residual sheet thickness, an increased difference between the two sides right and left can be detected for both kinematic models investigated, which is also due to the tilting of the rivet. In addition, the differences in the residual sheet thickness between the two sides tend to increase with increasing tumbling angle, as the rivet is driven further into the joint. This also explains the rivet head end positions. The greater the tumbling angle, the deeper the rivet head end position is, and in some cases it is even below the sheet metal plane, which provides the reference for the measurements. Again, the tilting of the rivet can be identified by the differences between the right and left measured values. The deep rivet head end positions allows a correlation between the tumbling angle and the end position of the traverse of the universal testing machine to be detected. The results show that with increasing tumbling angle, the end position of the traverse can be selected lower to achieve comparable values of the rivet head end positions as for smaller tumbling angles.
In Fig. 12, the geometries of the rivet heads are shown in section by an optical measurement with a 3D-profilometer. In this illustration, the results from the previous paragraph are reproduced in the form of the tilting of the rivet element in the joint. Furthermore, the conical shape of the rivet head can be clearly seen, which is characterised by an increasing height of the rivet head with increasing radius. This shape is created by the punch geometry and becomes more shallow with increasing tumbling angle, as the punch displaces more material in the radially external zone. The tilting described above can also be seen here, as well as the rivet head end positions below the sheet plane with a constant traverse end position of the joining process. From the results, a considerable influence of the kinematics and the angle on the process is recognisable and, through targeted adaptation of the tumbling strategy, a versatile joining of semi-tubular self-pierce riveted joints can be enabled, as targeted material flow control is possible with a tumbling process.
5 Conclusion and outlook
This article presents a tool for the manufacturing of tumbling semi-tubular self-piercing riveting joints. The tool is used to investigate mono- and multi-material joints with varying mechanical and geometric properties. An aluminium EN AW-6014 with 2.0 mm sheet thickness and a steel HCT590X+Z with 0.8 mm sheet thickness are utilised for the examinations. During the investigations, the influence of individual parameters of the tumbling strategy are identified. On the one hand, the tumbling angle is varied in steps between 0° and 6° and on the other hand, spiral and circular tumbling kinematics are applied.
Some important conclusions can be summarised as follows:
-
1.
The design of the tumbling tool enables the investigation of the versatility of tumbled semi-tubular self-piercing riveting joints due to the adaptable tumbling strategies.
-
2.
Investigations of joining processes with mono- and multi-material joints show a significant influence of the tumbling angle in terms of reduced force levels and of the tumbling kinematics through a more homogeneous increase in force on the force–displacement curve.
-
3.
The tumbling strategy influences geometric joint properties such as the undercut, the residual sheet thickness and the rivet head end position.
-
4.
The tumbling angle of α = 6° shows itself in this material and joining process combination as a process limit because of occurring cracks in the rivet shaft.
In order to investigate the versatility of the investigated process combination, additional process parameters have to be observed. First of all, the occurrence of the cracks must be investigated in more detail and the process parameters that significantly cause crack formation must be identified. Furthermore, the influence of the thickening shaft on the strength of the joint must be considered to possibly use it in a targeted way. In addition, investigations with total sheet thicknesses close to each other should be conducted in order to be able to recognise the influence of the geometric parameters of the joining points.
References
European Union (2019) The European green deal. Communication from the commission to the European Parliament, the European Council, the European Economic and Social Committee and the Committee of the Regions, Brussels
European Environment Agency (2020) Topics—mobility sector
European Parliament and of the Council (2019) Regulation (EU) 2019/631 of the European Parliament and of the Council of 17 April 2019 setting CO2 emission performance standards for new passenger cars and for new light commercial vehicles
Allwood J, Cullen JM (2012) Sustainable materials: With both eyes open; [future buildings, vehicles, products and equipment—made efficiently and made with less new material. UIT Cambridge, Cambridge, p 373
Mori K-I, Bay N, Fratini L, Micari F, Tekkaya AE (2013) Joining by plastic deformation. CIRP Ann 62(2):673–694
Heggemann T, Homberg W (2019) Deep drawing of fiber metal laminates for automotive lightweight structures. Compos Struct 216:53–57
Lai M, Brun R (2007) Latest developments in sheet metal forming technologies and materials for automotive application: the use of ultra high strength steels at Fiat to reach weight reduction at sustainable costs. In: Micari F, Geiger M (eds) Sheet metal 2007. Proceedings of the 12th international conference held at the University of Palermo, Italy, April 1st–4th 2007 ; [SheMet 2007, vol. 344. Trans Tech Publ, Stafa-Zürich, pp 1–8
Martinsen K, Hu SJ, Carlson BE (2015) Joining of dissimilar materials. CIRP Ann 64(2):679–699
He X, Pearson I, Young K (2008) Self-pierce riveting for sheet materials: state of the art. J Mater Process Technol 199(1–3):27–36
Meschut G, Janzen V, Olfermann T (2014) Innovative and highly productive joining technologies for multi-material lightweight car body structures. J Mater Eng Perform 23(5):1515–1523
DVS—Deutscher Verband für Schweißen und verwandte Verfahren, 2019. DVS-EFB 3410:2019-02 self-pierce riveting—overview. In: DVS Media GmbH, Düsseldorf, Berlin
Groche P, Fritsche D, Tekkaya EA, Allwood JM, Hirt G, Neugebauer R (2007) Incremental bulk metal forming. CIRP Ann 56(2):635–656
Merklein M, Allwood JM, Behrens B-A, Brosius A, Hagenah H, Kuzman K, Mori K, Tekkaya AE, Weckenmann A (2012) Bulk forming of sheet metal. CIRP Ann 61(2):725–745
Plancak ME, Vilotic DZ, Stefanovic MC (2012) Orbital forging—a plausible alternative for bulk metal forming. J Trends Dev Mach 16:35–38
Standring PM (1999) The significance of nutation angle in rotary forging. In: Proceedings of the 6th international conference on technology of plasticity, pp 1739–1744
Thoms V, Six S, Westkämper E, Breckweg A (eds) (2003) Stanznieten mit überlagerter Bewegung, Hannover
Huang H, Du D, Chang BH, Sui B, Chen Q (2007) Distortion analysis for self-piercing riveting of aluminium alloy sheets. Sci Technol Weld Join 12(1):73–78
Acknowledgements
This work was supported by the German Research Foundation (DFG) within the scope of the Transregional Collaborative Research Centre 285 on Method development for mechanical joinability in versatile process chains in the subproject C02 Versatile joining with a fastener—Project-ID 418701707.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
Conceptualisation: SW, ML, FK. Methodology: SW, ML. Formal analysis and investigation: SW, FK. Writing—original draft preparation: SW, FK. Writing—review and editing: ML, MM. Funding acquisition: ML, MM. Resources: MM. Supervision: ML, MM. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wituschek, S., Kappe, F. & Lechner, M. Investigation of the influence of varying tumbling strategies on a tumbling self-piercing riveting process. Prod. Eng. Res. Devel. 16, 353–362 (2022). https://doi.org/10.1007/s11740-021-01099-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-021-01099-3