Predicting regenerative chatter in milling with hardware-in-the-loop simulation using a dexel-based cutting model

Abstract

This article proposes a new model for simulating the interaction between cutting process and machine tool in real-time. The purpose of the model is to be coupled with a real CNC (by using hardware-in-the-loop simulation) in order to consider process forces and to predict regenerative chatter vibrations during virtual commissioning. Therefore a dexel-based workpiece model with adaptive resolution is used for the computation of the chip thickness respectively the cutting forces based on the actual machine tool position and the machining progress on the workpiece. Several simulation experiments are performed to validate the model and to analyze its numerical limits, such as computational accuracy and efficiency. The capability of the model to predict chatter is proven by comparing the simulated critical depth of cut with an analytical solution of the stability lobes. Therefore the dynamics of the machine tool were approximated as a single degree of freedom (SDOF) oscillator. A concluding analysis of the real-time factor confirms the model’s ability to be integrated under hard real-time requirements and with cycle times of just a few milliseconds which are typical of CNCs.

1 Introduction

The prediction of the machine tool behavior via simulation in consideration of the cutting process has been one of the most important research topics in production engineering within the last decades. The challenges of simulating the entire machine tool behavior are characterized by a diversity of different physical phenomena (e.g. flexible multibody systems, non-linear process forces, heat transfer) which have to be partially modeled in detail depending on the individual problem as described by Altintas et al. [1]. Especially process simulation places high demands on the utilized simulation tools. For the simulation-based prediction of process forces and process stability, e.g. chatter stability in milling, expert knowledge of the process itself and its simulation is required as shown by Brecher [2]. The prediction of the dynamical stability of cutting processes such as turning, milling and drilling processes has been investigated since the 1950s by Tlusty [3], Tobias [4] and Merrit [5]. Analytical approaches were introduced by Altintas in numerous publications. A good description of an analytical method for predicting the dynamical stability of milling processes is found in [6, 7]. Numerical methods were presented and improved by Henninger [8] and Chanda [9].

The application of simulation models in connection with real control systems has become widely popular in many fields of research and development in the recent years. Starting with the hardware-in-the-loop-simulation for virtual commissioning of control systems by Pritschow [10], up to simulation-based control functionalities such as condition monitoring or model-predictive path planning algorithms by Verl [11]. Further results were presented by Röck using reduced structural dynamic models [12] and process machine interaction models [13]. In all cases, a time-deterministic and highly efficient computation of the machine behavior is required. The interaction between cutting process and machine tool has a decisive impact on the process results and cannot be neglected in a simulation used for a process-oriented set-up. The actual cutting forces depend highly on the velocity profiles generated by the computer numerical control (CNC) and vary significantly subject to the CAD/CAM process, the control parametrization and the chosen CNC system. This leads to different mechanical excitations of the controlled machine tool and, consequently, to different process results which can only be predicted via a control-coupled simulation in real-time. Figure 1 shows a hardware-in-the-loop simulation scheme for virtual commissioning of real CNC systems.

Fig. 1

Hardware-in-the-loop simulation scheme for virtual commissioning of real CNC systems. The simulation results are used by the operator to manually adjust the CNC program and the cutting parameters (dashed line)

In this paper a new approach for modelling cutting processes for real-time simulation in order to consider process forces and predict process instability during virtual commissioning is presented. The main benefit of the proposed model over analytical approaches is that it can be used for virtual commissioning of a real CNC program with changing cutting conditions (e.g. transition from zero to full immersion when entering the workpiece, variable feed rates, variable tool penetration depths). In contrast, analytical approaches are only capable of calculating the stability for the static case (settled state) without considering changing cutting conditions (only full immersion with constant feed rate and constant penetration depth).

To make this possible, process forces under real dynamic cutting conditions have to be taken into account which in consequence requires a model that keeps track of the workpiece’s current state. Hence a dexel-based workpiece model with adaptive resolution is developed for the computation of the chip thickness based on the actual machine tool position and the machining progress on the workpiece. The proposed approach in this paper is limited to planar milling processes but will be extended to geometrically more complex cutting processes in future work.

2 The planar process force model

2.1 Dexel based cutting model for computation of the chip thickness

The geometry of the workpiece is approximated using a defined arrangement of so-called dexels. A single dexel represents a (bounded) ray passing through the workpiece and is geometrically described as a static segment of the straight line

$${\overset{\rightharpoonup}{r}}_{i}={\overset{\rightharpoonup}{r}}_{b,i}+\lambda \left({\overset{\rightharpoonup}{r}}_{e,i}-{\overset{\rightharpoonup}{r}}_{b,i}\right)$$

(1)

with ${\overset{\rightharpoonup}{r}}_{b,i}\in {\mathbb{R}}^{2}$ being its start point and ${\overset{\rightharpoonup}{r}}_{e,i}\in {\mathbb{R}}^{2}$ being its end point. Depending on the placement and the length of the individual dexels, differently shaped workpieces can be modeled. The workpiece model in this paper is limited to two dimensions for simulating planar milling processes. In this case, the workpiece is represented as a parallel arrangement of dexels on a plane and each of the tool’s cutting edges is a point projected onto this plane.

The path of the $j$-th cutting edge ${\overset{\rightharpoonup}{e}}_{j}$ created by the tool rotation is approximated as a linear interpolation between its current position ${\overset{\rightharpoonup}{e}}_{j,n}$ at time ${t}_{n}$ and its previous position ${\overset{\rightharpoonup}{e}}_{j,n-1}$ at time ${t}_{n}-\Delta t$ with the constant time step size $\Delta t$:

$${\overset{\rightharpoonup}{p}}_{j,n}={\overset{\rightharpoonup}{e}}_{j,n-1}+\mu \left({\overset{\rightharpoonup}{e}}_{j,n}-{\overset{\rightharpoonup}{e}}_{j,n-1}\right)$$

(2)

A collision detection between workpiece and tool identifies those dexels ${\overset{\rightharpoonup}{r}}_{i}$ which intersect with the path ${\overset{\rightharpoonup}{p}}_{j,n}$ of each cutting edge ${\overset{\rightharpoonup}{e}}_{j}$. All the dexels in between the current and the previous position of the cutting edge are cutting dexels (Fig. 2).

Fig. 2

Collision detection between cutting edge and workpiece dexels

The point of intersection ${\overset{\rightharpoonup}{c}}_{ij,n}$ between dexel ${\overset{\rightharpoonup}{r}}_{i}$ and path ${\overset{\rightharpoonup}{p}}_{j,n}$ of the $j$-th cutting edge is found by equating Eqs. (1) and (2)

$${\overset{\rightharpoonup}{c}}_{ij,n}={\overset{\rightharpoonup}{r}}_{b,i}+{\lambda }_{i}\left({\overset{\rightharpoonup}{r}}_{e,i}-{\overset{\rightharpoonup}{r}}_{b,i}\right)={\overset{\rightharpoonup}{e}}_{j,n-1}+{\mu }_{j}\left({\overset{\rightharpoonup}{e}}_{j,n}-{\overset{\rightharpoonup}{e}}_{j,n-1}\right).$$

(3)

After rewriting Eq. (3) we get a linear system of equations with the unknowns ${\lambda }_{i}$ and ${\mu }_{j}$:

$$\left[\begin{array}{cc}{\overset{\rightharpoonup}{r}}_{e,i}-{\overset{\rightharpoonup}{r}}_{b,i}& {\overset{\rightharpoonup}{e}}_{j,n-1}-{\overset{\rightharpoonup}{e}}_{j,n}\end{array}\right]\left(\begin{array}{c}{\lambda }_{i}\\ {\mu }_{j}\end{array}\right)={\overset{\rightharpoonup}{e}}_{j,n-1}-{\overset{\rightharpoonup}{r}}_{b,i}$$

(4)

Only if the solutions of both ${\lambda }_{i}$ and ${\mu }_{j}$ are between 0 and 1, the dexel ${\overset{\rightharpoonup}{r}}_{i}$ intersects with the cutting edge path ${\overset{\rightharpoonup}{p}}_{j,n}$:

$$0\le {\lambda }_{i}\le 1 \,and\, 0\le {\mu }_{j}\le 1 \rightarrow {\overset{\rightharpoonup}{c}}_{ij,n}={\overset{\rightharpoonup}{r}}_{i}\left({\lambda }_{i}\right)={\overset{\rightharpoonup}{p}}_{j,n}\left({\mu }_{j}\right).$$

(5)

The partial chip thickness ${h}_{ij,n}$ of each dexel ${\overset{\rightharpoonup}{r}}_{i}$ can be approximated as the scalar projection of the truncated dexel section $\Delta {\overset{\rightharpoonup}{r}}_{ij,n}={\overset{\rightharpoonup}{c}}_{ij,n}-{\overset{\rightharpoonup}{r}}_{b,i}$ on the connecting line ${\overset{\rightharpoonup}{c}}_{ij,n}-{\overset{\rightharpoonup}{r}}_{TCP,n}$ between the points of intersection ${\overset{\rightharpoonup}{c}}_{ij,n}$ and the tool center point ${\overset{\rightharpoonup}{r}}_{TCP,n}$ (Fig. 2). Thus, the chip thickness ${h}_{j,n}$ of the $j$-th cutting edge is the arithmetic average of all ${h}_{ij,n}$ over the cutting dexels with indices ${i}_{b}\le i\le {i}_{e}$.

$${h}_{ij,n}=\left|\frac{{\left({\overset{\rightharpoonup}{c}}_{ij.n}-{\overset{\rightharpoonup}{r}}_{TCP.n}\right)}^{T}\Delta {\overset{\rightharpoonup}{r}}_{ij,n}}{\left|{\overset{\rightharpoonup}{c}}_{ij,n}-{\overset{\rightharpoonup}{r}}_{TCP,n}\right|}\right| \Rightarrow {h}_{j,n}=\frac{1}{{i}_{e}-{i}_{b}}\sum_{i={i}_{b}}^{{i}_{e}}{h}_{ij,n}$$

(6)

For material removal the start point of the dexel has to be updated to ${\overset{\rightharpoonup}{r}}_{b,i}={\overset{\rightharpoonup}{c}}_{ij,n}$.

If the cutting edge path ${\overset{\rightharpoonup}{p}}_{j,n}$ is located between two dexels, ${h}_{ij,n}$ cannot be calculated directly by the intersection point ${\overset{\rightharpoonup}{c}}_{ij,n}$. This problem occurs if the spindle speed or the time step size of the simulation is small. For varying tool paths, feed rates and spindle speeds it is not possible to predict all cutting edge positions in advance to be able to initialize a sufficient number of dexels located at the right positions before the simulation starts. It is also not feasible to fill the whole workpiece with just enough uniformly spaced dexels without losing computational efficiency. The only way to solve this problem is to adapt the density of dexels during runtime by inserting a new dexel exactly on the current position ${\overset{\rightharpoonup}{e}}_{j,n}$ of the cutting edge if no dexel is available. This approach converges to an optimized distribution of dexels within the workpiece and simultaneously improves the approximation of the chip thickness especially in areas where high dexel density is needed. Figures 3 and 4 show the evolution of the number of dexels during the penetration of a tool with $N=10$ teeth and a radius of ${r}_{T}=0.01 [m]$ in a rectangular workpiece with initially ${N}_{D}=20$ dexels. The number of dexels increases until the tool has completely penetrated into the workpiece (Fig. 4).

Fig. 3

Evolution of the number of dexels (dark areas represent a high density of dexels)

Fig. 4

Number of dexels over tool penetration. The number of dexels increases until the tool has completely penetrated at 0.01 m (corresponds the tool radius ${r}_{T}$)

2.2 Cutting forces

The radial and tangential cutting forces acting on each cutting edge depend on the chip thickness ${h}_{j,n}$ at time ${t}_{n}$ and can be calculated by:

$$\begin{array}{l}{F}_{rj,n}={k}_{r}a{h}_{j,n}\\ {F}_{tj,n}={k}_{t}a{h}_{j,n},\end{array}$$

(7)

with the radial and tangential cutting coefficients ${k}_{r}$ and ${k}_{t}$ and the depth of cut $a$ [6]. After summing up all cutting edge forces and transforming them into xy-coordinates by using the rotation matrix $\Phi \left({\phi }_{j,n}\right)$ of the $j$-th tooth we get the total forces acting on the tool

$$\left(\begin{array}{c}{F}_{x,n}\\ {F}_{y,n}\end{array}\right)=\sum_{j=0}^{N-1}\left[\Phi \left(\Omega {t}_{n}+\frac{2\pi }{N}j\right)\right]\left(\begin{array}{c}{F}_{rj,n}\\ {F}_{tj,n}\end{array}\right)$$

(8)

and the resulting axial torque

$${T}_{n}={r}_{T}\sum_{j=0}^{N-1}{F}_{tj,n}.$$

(9)

with the tool radius ${r}_{T}.$ Figure 5 shows the acting forces on the cutting edges respectively on the tool center point.

Fig. 5

Calculated forces acting on the tool

3 Simulation results

3.1 Static force simulation

In the following various simulation results in time domain will be presented. It will be shown that based on the dexel model valid forces for milling processes can be computed. Moreover, the numerical influence of the simulation time step size $\Delta t$ and the spindle speed ${\Omega}$ will be discussed. To validate the simulated milling process forces it is sufficient and more comprehensible to consider only one tooth (Fig. 6) with the parameters in Table 1. It should be noted at this point that the main focus of this simulation was not on the analysis of a real-world process, but rather on validating the method. Therefore the values in Table 1 were chosen to represent a convenient parameterization for machining light metals (e.g. aluminium).

Fig. 6

Milling simulation with one tooth for model validation

Table 1 Parameters used to validate the dexel-based cutting forces

To validate the dexel-based cutting forces a comparison against the “exact” analytically calculated forces is performed. Thus the exact chip thickness for one tooth is given by

$$h\left(\Omega t\right)=\left[{v}_{x}\cdot {\tau }_{rev}\cdot \mathrm{cos}\left(\Omega t\right)\right]\cdot g\left(\Omega t\right)$$

(10)

with the feed rate ${v}_{x}$, the time period for one spindle revolution ${\tau }_{rev}$ and the spindle speed $\Omega .$ The unit step function $g\left(\Omega t\right)$ depends on the angular position of the cutting edge $\Omega t$ and determines whether the tooth is in or out of cut.

$$\begin{array}{l}g\left(\Omega t\right)=1 \leftarrow -0.5\pi <\Omega t\mathrm{mod}\left(2\pi \right)<+0.5\pi \\ g\left(\Omega t\right)=0 \leftarrow \mathrm{otherwise}.\end{array}$$

(11)

The exact cutting forces can then be calculated with Eq. (8):

$$\left(\begin{array}{c}{F}_{x,ex}\\ {F}_{y,ex}\end{array}\right)=\left[\Phi \left(\Omega t\right)\right]\left(\begin{array}{c}{k}_{r}\\ {k}_{t}\end{array}\right)\cdot a\cdot h\left(\Omega t\right)$$

(12)

For each tool rotation the maximum chip thickness is reached at an angle of $\Omega t\mathrm{mod}\left(2\pi \right)=0 [rad]$. Assuming a spindle speed of ${\Omega}=2000\left[{rev}/{min}\right]$ and a feed rate of ${v}_{x}=0.01\left[{m}/{s}\right]$, the time period for one spindle revolution is ${\tau }_{rev}=60 [s/\mathit{min}]/2000 [rev/min]= 0.03 [s/rev]$ and the maximum chip thickness results in

$$h\left(0\right)=\left[{v}_{x}\cdot {\tau }_{rev}\cdot \mathrm{cos}\left(0\right)\right]\cdot g\left(0\right)=\left[0.01\left[\frac{m}{s}\right]\cdot 0.03\left[\frac{s}{rev}\right]\cdot 1\right]\cdot 1=3\cdot {10}^{-4}\left[\frac{m}{rev}\right].$$

(13)

The cutting force can then be calculated to

$$\left(\begin{array}{c}{F}_{x,ex}\\ {F}_{y,ex}\end{array}\right)=\left[\begin{array}{cc}-\mathrm{cos}\left(0\right)& +\mathrm{sin}\left(0\right)\\ -\mathrm{sin}\left(0\right)& -\mathrm{cos}\left(0\right)\end{array}\right]\left(\begin{array}{c}{k}_{r}\\ {k}_{t}\end{array}\right)\cdot a\cdot h\left(0\right)=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]\left(\begin{array}{c}0.6\cdot {10}^{8}\\ 1.0\cdot {10}^{8}\end{array}\right)\cdot 0.01\cdot 3\cdot {10}^{-4}=\left(\begin{array}{c}-180\left[N\right]\\ -300\left[N\right]\end{array}\right).$$

(14)

Comparing the results of one full revolution $-\pi <\Omega t\mathrm{mod}\left(2\pi \right)<\pi$, the simulated dexel-based cutting forces ${F}_{x,sim},{F}_{y,sim}$ show a good correlation with the analytically calculated exact forces ${F}_{x,ex},{F}_{y,ex}$. Figure 7 shows the results with different simulation time step sizes $\Delta t$.

Fig. 7

Simulated process forces with $\Delta t=0.0005 [s]$ (top) resp. $\Delta t=0.001 [s]$ (bottom) and ${\Omega}=2000\left[{rev}/{min}\right]$

Figure 8 shows the influence of the spindle speed. The left picture demonstrates how a low spindle speed of ${\Omega}=200\,\left[{r}{e}{v}/{m}{i}{n}\right]$ (${{v}}_{{x}}=0.001\,\left[{m}/{s}\right]$) supports a very high accuracy of the simulation results in consequence of the dexel adaptation. However, the right picture shows the result in case of high spindle speeds, e.g. ${\Omega}=4000\,\left[{r}{e}{v}/{m}{i}{n}\right]$ (${{v}}_{{x}}=0.02\,\left[{m}/{s}\right]$). The error comes from the gross path discretization which is directly coupled with the time step size and the spindle speed. Reducing the time step size gives more accurate results but at the same time worsens the computational efficiency.

Fig. 8

Simulated process forces with $\Delta t=0.001 [s]$ and ${\Omega}=200\left[{rev}/{min}\right]$ (left) and ${\Omega}=4000\left[{rev}/{min}\right]$ (right)

Figure 8 highlights the importance of knowing the accuracy of the model in dependence of the spindle speed. To quantify the error we use the absolute differences between the simulated and the exact forces

$$\left|{F}_{ex}\right|=\sqrt{{F}_{x,ex}^{2}+{F}_{y,ex}^{2}}$$

$$\left|{F}_{sim}\right|=\sqrt{{F}_{x,sim}^{2}+{F}_{y,sim}^{2}}$$

$${\Delta F}_{err}=\left|\left|{F}_{ex}\right|-\left|{F}_{sim}\right|\right|$$

(15)

and define the percentual maximum error

$${E}_{max}=100\cdot \frac{\underset{-0.5\pi \le\Omega t\le 0.5\pi }{\mathrm{max}}\left({\Delta F}_{err}\right)}{\underset{-0.5\pi \le\Omega t\le 0.5\pi }{\mathrm{max}}\left(\left|{F}_{ex}\right|\right)}$$

(16)

and the percentual mean error

$${E}_{mean}=100\cdot \frac{\underset{-0.5\pi \le\Omega t\le 0.5\pi }{\mathrm{mean}}\left({\Delta F}_{err}\right)}{\underset{-0.5\pi \le\Omega t\le 0.5\pi }{\mathrm{max}}\left(\left|{F}_{ex}\right|\right)}.$$

(17)

Figure 9 shows the percentual maximum and mean error versus the spindle speed for different simulation step sizes with ${v}_{x}=0.02\left[{m}/{s}\right]$:

Fig. 9

Percentual maximum and mean error of the cutting force’s magnitude versus the spindle speed at different simulation step sizes

Assuming that a 10% maximum error and a 5% mean error is acceptable the simulation of the static forces at a simulation time step size of $\Delta t=0.001 [s]$ can be used up to a spindle speed of roughly ${\Omega}=1800\left[{Rev}/{min}\right]$, at $\Delta t=0.0005 [s]$ up to roughly ${\Omega}=3000\left[{Rev}/{min}\right]$ and at $\Delta t=0.0002 [s]$ up to ${\Omega}=7000\left[{Rev}/{min}\right]$.

To complete the validation for the milling process it is necessary to compare simulation results with more than one cutting tooth. Therefore the scenario from Fig. 6 and Table 1 is used again, but this time with $N=2$ and $N=4$ teeth, and at spindle speeds of ${\Omega}=200\left[{rev}/{min}\right]$ (${v}_{x}=0.001\left[{m}/{s}\right]$) and ${\Omega}=2000\left[{rev}/{min}\right]$ (${v}_{x}=0.01\left[{m}/{s}\right]$). The simulation time step size is $\Delta t=0.001 [s]$. The results are shown in Figs. 10 and 11:

Fig. 10

Simulated process forces with $N=2$ and ${\Omega}=200\left[{rev}/{min}\right]$ (left) and ${\Omega}=2000\left[{rev}/{min}\right]$ (right). The simulation step size is $\Delta t=0.001 [s]$

Fig. 11

Simulated process forces with $N=4$ and ${\Omega}=200\left[{rev}/{min}\right]$, $\Delta t=0.001 [s]$ (left); ${\Omega}=2000\left[{rev}/{min}\right]$, $\Delta t=0.001 [s]$ (middle); ${\Omega}=2000\left[{rev}/{min}\right]$, $\Delta t=0.0002 [s]$ (right)

For milling processes with $N=4 \,( N=6, N=8, N=10, \dots )$ constant cutting forces occur if the tool is completely penetrated in the workpiece. In that case the error caused by a gross path discretization due to large spindle speeds or large simulation time step sizes becomes crucial. This can be seen in the middle picture of Fig. 11. These errors are not acceptable and the only way to avoid them is to reduce the time step size, as demonstrated in the right picture of Fig. 11.

3.2 Dynamic force simulation

In the previous sections, it was assumed that the machine tool is absolutely stiff and no vibrations occur. In the following the model of the tool has been extended to a single mass oscillator to consider the first natural frequency of structural dynamics.

3.2.1 Single degree of freedom (SDOF) vibration model

To validate the dynamic forces and the ability to predict the chatter phenomenon in milling a SDOF model which covers the tool vibrations in feed direction is used. It is described as a single mass oscillator with a spring-damper element between the tool center point and the tool holder excited by the cutting force (Fig. 12). The equation of motion can be given by

$$\ddot{x}+2D{\omega }_{0}\dot{x}+{\omega }_{0}^{2}x={\omega }_{0}^{2}u+\frac{{\omega }_{0}^{2}}{{k}_{0}}{F}_{x}\left(x,\Omega ,a,\dots \right),$$

(18)

where $x$ denotes the tool position and ${F}_{x}$ the cutting force in feed direction computed by the dexel model. $u$ represents the target position of the tool (commanded by the CNC), ${\omega }_{0}$ the natural eigenfrequency, $D$ the damping ratio and ${k}_{0}$ the stiffness of the spindle-tool system.

Fig. 12

SDOF vibration model

Because of the hard real-time requirements in a CNC-coupled hardware-in-the-loop simulation, a very efficient time integration method—the double shot semi-implicit Euler method—is used to solve Eq. (18). With ${x}_{n}={x}_{0}$ and ${v}_{n}={\dot{x}}_{0}$ as the initial condition, the following integration scheme is executed for each time step ${t}_{n+1}={t}_{n}+\Delta t$:

$${a_n}=-2D{\omega }_{0}{v}_{n}-{\omega }_{0}^{2}{x}_{n}+{\omega }_{0}^{2}{u}_{n}+\frac{{\omega }_{0}^{2}}{{k}_{0}}{F}_{x,n}$$

$${v}_{n+\frac{1}{2}}={v}_{n}+\frac{\Delta t}{2}{a}_{n}$$

$${x}_{n+\frac{1}{2}}={x}_{n}+\frac{\Delta t}{2}{v}_{n+\frac{1}{2}}$$

$${a}_{n+\frac{1}{2}}=-2D{\omega }_{0}{v}_{n+\frac{1}{2}}-{\omega }_{0}^{2}{x}_{n+\frac{1}{2}}+{\omega }_{0}^{2}{u}_{n}+\frac{{\omega }_{0}^{2}}{{k}_{0}}{F}_{x,n}$$

$${v}_{n+1}={v}_{n+\frac{1}{2}}+\frac{\Delta t}{2}{a}_{n+\frac{1}{2}}$$

$${x}_{n+1}={x}_{n+\frac{1}{2}}+\frac{\Delta t}{2}{v}_{n+1}$$

(19)

The explicit scheme in Eq. (19) requires only one evaluation of ${F}_{x}$ per time step, which is the computationally most expensive part of the calculation. This leads to a very fast solution and enables the use of small simulation time step sizes $\Delta t$.

3.2.2 Transient results

The transient simulation shows the process forces while the tool penetrates into the workpiece. Based on the earlier introduced parameters (see Table 1), the extended parameter list in Table 2 is used in the following.

The simulation results are shown in Fig. 13 with ${a}=0.01[{m}]$ (process stable) and in Fig. 14 with ${a}=0.03[{m}]$ (process unstable). Because of the tool’s symmetry with ${N}=10$ the force ${{{F}}}_{{\varvec{x}}}$ becomes constant if the tool has completely penetrated into the workpiece and the process is stable (Fig. 13). In case of instability the force ${F}_{x}$, and therefore also the tool position ${x}$, starts oscillating with the chatter frequency ${\omega}_{c}\approx 530\left[{rad}/{s}\right]$ which is close to the natural frequency ${\omega}_{0}=500\left[{rad}/{s}\right]$ of the SDOF model. In that case the tool jumps out of cut and the force periodically becomes zero (zero cut)—regenerative chatter occurs (Fig. 14).

Fig. 13

Transient simulation with ${a}=0.01[{m}]$. The process is stable

3.2.3 Process stability lobes

The reliable prediction of chatter vibrations as shown in Fig. 14 is very important for the virtual commissioning of milling processes. The following results verify the predictability of stability lobes with the SDOF vibration model combined with the dexel-based cutting force model from Fig. 12. Again, the simulation scenarios shown in Figs. 13 and 14 are used, but this time with the parametrization from Table 2. The results are compared with the analytically calculated stability lobes based on the method presented by Altintas and Budak in [6]. The graph in Fig. 15 shows the depth of cut $a$ over the spindle speed $\Omega$ with the analytically calculated critical depth of cut ${a}_{\mathrm{lim}}$ (stability lobes) and stable/unstable simulation results based on the dexel model (Fig. 16).

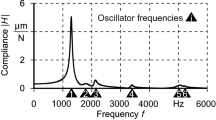
Figure 15 shows a very good correlation between the dexel-based approach and the analytical solution for spindle speeds between $\Omega =200 \left[rev/min\right]$ and $\Omega =600 \left[rev/min\right]$. A detailed representation of the forces ${F}_{x}$ with a spindle speed of $\Omega =600 \left[rev/min\right]$ is demonstrated in Fig. 17.

3.3 Real-time capability

The real-time capability is represented by the real-time factor (RTF) which is defined as

$$RTF=\frac{{t}_{CPU}}{{t}_{sim}}$$

(20)

where ${t}_{sim}$ denotes the simulation time interval and ${t}_{CPU}$ denotes the CPU time consumed to execute the simulation time interval. For real-time simulation, the RTF has to be less than 1. Figure 17 shows the RTF over the time for the simulation of the milling scenario shown in Fig. 12 with $\Omega =2000 [rev/min]$ and $\Delta t=0.001 [s]$. The RTF is nearly constant over time. Only at the start of the simulation, when the tool touches and enters the workpiece, the computational effort is varying due to the adjustment of the number of dexels.

Table 3 shows the $RTF$ and number of dexels ${N}_{D}$ with different parameters measured after ten seconds of simulation time.

The parameters which have an influence on the $RTF$ are the spindle speed ${\Omega}$, the simulation time step size $\Delta t$ and the number of teeth $N$. It can be shown that the $RTFs$ increase with both growing spindle speed and number of teeth because of the increasing number of cutting dexels (see Fig. 2) to be considered per time step within the calculation of the chip thickness. For low spindle speeds and small simulation time step sizes the large number of adapted dexels becomes computationally dominant and the $RTFs$ increase as well.

To demonstrate the method’s boundaries in terms of computational capacity on a certain hardware setup, Table 3 also covers parameter settings resulting in $RTFs$ greater than 1.

4 Conclusion and outlook

In this article a new approach for simulating planar cutting processes and predicting chatter vibrations in real-time was introduced. The cutting forces were simulated by using a dexel-based workpiece model for the calculation of the chip thickness. The number of dexels is adapted at runtime and converges to an sufficiently accurate spatial discretization of the workpiece. Thereby it is ensured that the chip thickness can also be calculated for varying cutting conditions and for arbitrary simulation time step sizes. Several scenarios for static and dynamic force simulation were validated by comparing the results with analytical solutions. Beyond that, a quantitative analysis of the method’s computational efficiency via the real-time factor (RTF) confirmed its ability to be executed under hard real-time requirements.

One of the main advantages of using geometry-based models simulated in the time domain is that more complex applications with changing cutting conditions and arbitrary workpiece geometries can be considered. Currently the proposed model is being adapted on an out-of-round turning process whose first results are shown in Fig. 18. Out-of-round turning is characterized by permanently changing cutting conditions and unsteady process forces that can only be modelled using numerical approaches such as the here proposed method.

Fig. 14

Transient simulation with ${a}=0.03[{m}]$. The process is unstable

Fig. 15

Correlation of process stability between dexel-based model and analytically derived stability lobes

Fig. 16

Dexel-based cutting force validation near the stability limit with the critical depth of cut ${a}_{lim}=16.6 \left[mm\right]$ at the exemplary spindle speed $\Omega =600 \left[rev/min\right]$ (see Fig. 15)

Fig. 17

Real-time factor ($RTF$) of an exemplary milling simulation

Fig. 18

Simulation of an out-of-round turning application as an example of a process with permanently changing cutting conditions and unsteady forces

Table 2 Parameters used for simulations with dynamic forces

Table 3 Real-time factor ($RTF$) and number of dexels ${N}_{D}$ depending on the spindle speed ${\Omega}$, the simulation time step size $\Delta t$ and the number of teeth $N$, computed on Intel Core i7-8750H, 2,20 GHz, 16 GB RAM, Windows 10, 64 bit

Another improvement will be the extension of the model for 3D processes coupled on multi degree of freedom (MDOF) machine dynamic models.