The treatment of musculoskeletal disorders through a total shoulder arthroplasty (TSA) continues to be a challenging issue that still exhibits higher failure and revision rates than hip or knee arthroplasty [1,2,3,4]. Preparation of the glenoidal surface to ensure adequate seating of the implant and accurate implant positioning is a complex task. Incorrect or imprecise placement of the implant can lead to pain, functional limitations, and either instability or early glenoid implant loosening [5].

In recent years, numerical models have been used to address different problems with glenoid implants. However, the implant position with respect to the degree of glenoid reaming and implant depth has not yet been analysed. To the best of the authors’ knowledge, no studies, with the exception of a finite element analysis (FEA) using a cementless implant [6], have addressed this issue. The analysis of only two positions (neutral and 3.0 mm) demonstrated that the implant depth has a significant influence on the interface micromotions. Consequently, although the influence of implant depth on bone ingrowth was noted, the effect was found to be unrelated to the surrounding bone density.

The stress within the cement mantle has been shown to be essential for primary stability of a glenoid implant [7]. Using a three-dimensional (3D) model, various cement thicknesses were investigated by evaluating the stress within the cement mantle and the micromotions at the bone–cement interface. The results showed that the optimal cement thickness is between 1.0 and 1.5 mm [8]. A load-bearing function of subchondral bone has been suggested and was confirmed in a cadaveric study using pristine and cancellous-free specimens that found a strength decrease under the subchondral bone plate of 25% at 1.0 mm and 70% at 2.0 mm [9]. Although a commonly known surgical guideline is to preserve as much subchondral bone as possible [10, 11], the biomechanical mechanisms that regulate the interaction between subchondral bone and a cemented glenoid implant are not well elucidated.

The present study focused on the impact of excessive reaming on a cemented glenoid component using FEA. An anatomically precise 3D model of a scapula was developed, and the bone density distribution was integrated accordingly. A cemented all-polyethylene glenoid implant was inserted at increasing implant depths to simulate different degrees of reaming. The resultant von Mises stresses and micromotions were analysed at the bone–cement interface according to their contribution to implant stability, fatigue and bone formation. It is hypothesised that the degree of reaming has a considerable influence on the mechanical behaviour of the implant and its fixation. The gained insights might contribute to a surgeon’s optimal decision regarding glenoid preparation and implant position and thus influence the subsequent longevity of the glenoid implant.

Methods

Three-dimensional modelling

The first step in an FEA study is development of an accurate 3D model. A CT scan of a shoulder complex (male, 71 years, 1 mm slice thickness) that shows no evidence of pathological changes was provided by the Salzburg County Hospital. The inclination and version angles (10.1 and 3.4°, respectively) of the glenoid were within normal ranges. Image segmentation techniques were applied using Mimics 13.0 (Materialise, Leuven, Belgium) to separate the cortical and trabecular bone structures from the surrounding soft tissue. Most of this separation was performed automatically, although manual refinement of the model was necessary in some regions of the scapula due to insufficient imaging of very thin sections of the scapula. After the refinement step, a 3D surface model was computed and imported into Solidworks (Dassault Systems, Vélizy-Villacoublay, France) to generate a solid model and perform angular measurements (e. g., inclination and version) and implant placement. Assessment of the glenoid is important for preoperative planning in shoulder surgery and for establishment of the 3D shoulder model. Therefore, Saller’s line, which is defined by the supraglenoid and infraglenoid tubercle, was used as a reference for accurate angular measurements and implant placement [12].

A computer-aided design (CAD) model of a keeled glenoid implant UniverseTM (Arthrex, München, Germany) was used, and full seating of the implant back was considered a major concern. The resulting implant positions were confirmed through surgical expertise. The implant depth was varied along a line orthogonal to Saller’s line. Four different implant positions were considered: 0.5, 1.0, 1.5 and 2.0 mm with respect to the optimal implant position (0.0 mm), which serves as a reference model.

Bone cement in the form of polymethylmethacrylate (PMMA) is commonly used for primary fixation of the glenoid component. Therefore, a cement template with a 1.0 mm thickness [8] was constructed and used for the subsequent virtual surgery. Additionally, a humeral head component with a radial mismatch of 6 mm was constructed; this component acts as a force transmitter onto the implant surface [13]. The established shoulder model was imported into the ANSYS 14.0 finite element (FE) software (Ansys Inc., Canonsburg, PA, USA), and all of the necessary Boolean operations were performed. Fig. 1 shows the final FE model.

Fig. 1
figure 1

Representation of the assembly of the final three-dimensional finite element model showing the scapula, the bone cement and the implant. The non-conforming humeral head component, which acts as a force transmitter, is also shown

Full size image

Bone density

Consideration of bone density is an important aspect during FEA of bone structures due to the varying distributions of bone density. Although various numerical models have been developed [14,15,16,17], the subsequently described approach developed by Gupta and Prosenjit [18] was used in this study, because it is the only existing model derived directly from scapular bone. A linear relationship between Hounsfield units (HU) derived from the CT scan and the bone density was established through calibration via linear regression, which resulted in the derivation of Eq. 1:

$$\rho =1.1187\cdot 10^{-3}\cdot \mathrm{HU}$$
(1)

In the next step, the computed bone density was transformed into Young’s modulus by addressing only the open and closed cell structures of the trabecular bone according to Eqs. 2 and 3:

$$E=1049.45\cdot 10^{-6}\cdot \rho ^{2}\,\mathrm{for}\,\rho \leq 0.35~\mathrm{g}/\mathrm{cm}^{3}$$
(2)
$$E=3\cdot 10^{-6}\cdot \rho ^{3}\,\mathrm{for}\,0.35\leq \rho \leq 1.80~\mathrm{g}/\mathrm{cm}^{3}$$
(3)

To ensure cortical stability, Gupta and Prosenjit [18] recommend the definition of a 2 × 0.5 mm homogenously layered shell of compact bone with a Young’s modulus of E = 17.500 MPa (=1.8 g/cm3). Because compact bone is not distributed homogeneously over the entire scapula, a modified cortical shell approach was used in this study. All HU values for the entire scapula were set to the maximum value, which corresponds to ρ = 1.8 g/cm3. Subsequently, only the HUs obtained from the previously segmented trabecular part were used. The HU values of compact bone were substituted with the values of the trabecular segmentation at the corresponding voxel coordinates using a customised search-and-replace routine. The derived Young’s moduli were then introduced into the Ansys software, and the bone density was therefore incorporated into the FE model.

Finite element model and boundary conditions

Development of an accurate FE mesh is a delicate part of FE simulations, because the accuracy of the result strongly depends on the quality of the FE mesh. All the models were meshed with quadratic tetrahedral elements (SOLID187, Ansys) using the meshing size control methods in Ansys to achieve a finer mesh resolution at important areas, such as bone cement and the glenoid region (see Fig. 2). The interfaces were meshed with 3D contact surface elements (CONTA714 and TARGET170, Ansys).

Fig. 2
figure 2

Results of the meshing procedure using SOLID187 (Ansys Inc., Canonsburg, PA, USA) elements and size control methods for a the glenoidal area, b the bone cement and c the glenoid implant

Full size image

A convergence study was performed using the h‑method and a centric load [19]. Although total convergence was not achieved for the scapula (deviation <3.5%) and bone cement (deviation <3.5%) due to computational limitations, a total of ~280,000 nodes was considered sufficient with respect to the degree of convergence, accuracy and solution time. Fixed supports were attached at the insertion points of the main participating muscles: trapezius muscle, rhomboid muscle, deltoid muscle, and serratus muscle anterior and inferior to the scapula [20]. Additionally, the model was fixed at a point near the inferior angle on the dorsal side of the scapula to represent contact with the thorax. These points of fixation are a sufficient distance apart to avoid any significant mechanical influence at the glenoid area.

The amount of force applied to the humeral head was defined by analysing the data provided by Bergmann et al. [21], who measured forces using an instrumented implant. This resulted in a mean of 650 N for flexion and abduction of 90°. According to the measured data, a shear force of one third of the mean force vector was used to initiate humeral head translation and therefore change the point of force application eccentrically on the implant surface. A non-linear frictional contact with a coefficient of μ = 0.07 was chosen between the humeral head and the implant surface [22]. The interface between the implant and the bone cement was considered fully bonded. A coefficient of μ = 0.6 was assumed for the interface between the bone and the bone cement [23, 24]. The peak penetration of both contacts (augmented Lagrange theory) was smaller than 2.7 × 10−3 mm and determined automatically by the FE software based on the geometry and the meshing at the contact surfaces.

The elasticity modulus of the ultra-high-molecular-weight polyethylene (UHMWPE) implant was E = 500 MPa (v = 0.4) [25]. Bone cement in the form of PMMA is considered elastic (E = 2000 MPa, v = 0.3) [25], similar to the humeral head component (CrCoMo, E = 230.000 MPa, v = 0.3) [26]. The elasticity modulus of the bone was related to the bone density, as described previously [18].

To quantify the extent of the differences between FEAs, the relative percentages of the corresponding mean von Mises stress values with respect to the reference model (0.0 mm) are shown. To evaluate the fatigue behaviour of bone cement, the tensile and compressive stresses, which play an important role and are commonly used as failure criteria (ASTM F451), are shown as the corresponding yield strengths.

Results

Reaming of the glenoid is necessary to ensure adequate seating and corresponds directly to the implant depth. To investigate the influence of implant position (implant depth), simulations with varying depths (0.5, 1.0, 1.5 and 2.0 mm) and centric and eccentric loading conditions were conducted and the influence of a particular implant depth investigated.

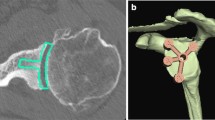
A keeled implant at the 0° version and natural inclination was inserted at the 0.0 mm implant depth and served as the reference model. According to Fig. 3a, it is clearly apparent that the implant depth of 0.0 mm preserved most of the subchondral bone (and thus meets the common surgical recommendations) and is regarded as the reference in the implant positioning process and virtual surgery. Fig. 3b through 3e show that mostly subchondral bone was removed if the implant was placed at depths in the range of 0.0 to 0.5 mm, whereas an implant depth in the range of 0.5 to 2.0 mm results in mostly cortical bone at the glenoid rim being removed. In contrast, a slightly higher trabecular bone density was present at the bottom of the resected hole for the implant keel.

Fig. 3
figure 3

Bone density distribution at the reamed glenoid surface of patient E with varying implant depths: a 0.0 mm (reference model), b 0.5 mm, c 1.0 mm, d 1.5 mm and e 2.0 mm

Full size image

Centric loading

According to the mean von Mises stress values, the scapula shows a decreasing behaviour with increasing implant depth to obtain a maximum difference of −17.2% at 2.0 mm. A similar trend was observed with the maximum von Mises stress, although substantially higher values were observed. In contrast, the mean and maximum stresses increase steadily within the bone cement and achieve their maximum deviations at the same implant depth (+9.9 and +34.8%, respectively). The values of the differences between the different implant depths with respect to the reference model (0.0 mm) are given in Tables 1 and 2.

Table 1 Relative difference between the mean von Mises stresses for the scapula and bone cement with varying implant depth. The values for the centric and the eccentric load cases are shown
Full size table
Table 2 Relative difference between the maximum von Mises stresses for the scapula and bone cement with varying implant depth. The values for the centric and the eccentric load cases are shown
Full size table

To evaluate the fatigue behaviour of bone cement, the values for tensile and compressive stress are provided. The maximum tensile stress was found to be 20.51 MPa for the reference model, and this value increases to 24.92 MPa at the 2.0 mm implant depth. For the reference model, the value of the maximum compressive stress was found to be 18.76 MPa, and this value increases to 20.02 MPa at the 2.0 mm implant depth. A remarkable difference was also observed in the tangential micromotions, with an increase of 28.0% from the reference model to the 2.0 mm implant depth. The bar plot of the mean tangential micromotions shown in Fig. 4a provides a distinctive illustration. Interestingly, the normal micromotions decreased by 18.6% from the reference model to the 2.0 mm implant depth, and this effect is also noticeable in Fig. 4b.

Fig. 4
figure 4

Bar plot exhibiting all implant depths with the corresponding mean a tangential and b normal micromotions. Both load cases (centric and eccentric) are shown

Full size image

Eccentric loading

Compared with the centric load case, the mean stress values for the scapula rise with increasing implant depth, whereas a trend similar to that observed in the centric load case (Table 1) was obtained within the bone cement. The maximum difference hereby occurs at the 2.0 mm depth. If the maximum difference between the maximum von Mises stress values is considered, which occurs at the 2.0 mm depth, +17.2% and 35.1% of the total difference is accounted for by the scapula and the bone cement, respectively (Table 2). The maximum values for tensile strength within the bone cement are 17.57 MPa (reference model) and 24.09 MPa (2.0 mm depth), and the compressive stress exhibits maximum values of 20.29 and 24.33 MPa, respectively.

In general, the behaviour of the micromotions in the eccentric load case is similar to that observed in the centric load case. The tangential micromotions increase steadily with increasing implant depth. These exhibit a +25.5% difference in the mean value and a +14.2% difference in the maximum value, but at a slightly lower level (see Fig. 4a). The normal micromotions show the opposite behaviour and decrease by a mean maximum of −14.2% between the reference model and the 2.0 mm implant depth (Fig. 4b).

The development of mean stress in the scapula and bone cement for both load cases is illustrated in Fig. 5a. In this illustration, the increasing and decreasing trends, as well as the higher stress values for the eccentric load case, are clearly apparent. In this context, the increase in mean stress for bone cement in both load cases is evident, as shown in Fig. 5b.

Fig. 5
figure 5

Bar plot exhibiting the implant depths with the corresponding mean von Mises stresses for a the scapula and b bone cement. Both load cases (centric and eccentric) are shown

Full size image

Discussion

Loss of glenoid bone often occurs in association with glenohumeral osteoarthritis. Therefore, the preservation of as much subchondral bone as possible during the surgical procedure of a TSA through the minimal resection of subchondral bone and adequate implant seating is an important surgical guideline [10, 11, 27,28,29]. The study conducted by Suárez et al. [6] is the only study to date that has addressed the possibility of an optimal and a deeper implant position. Other studies that have investigated glenoid implants and shoulder arthroplasty use a fixed implant depth and ignored possible variations in implant depth.

It is difficult to methodically quantify the amount of bone reaming that is necessary for adequate implant seating within a 3D model. Nevertheless, sample measurements at the region around the glenoid centre of the reference model showed a necessary resection depth of approximately 1.7 mm to ensure adequate seating of the implant for the reference model (0.0 mm). It can be observed in Fig. 3a–c that an additional reaming of 1.0 mm with respect to the implant position at 0.0 mm resects the entire subchondral bone. A study by Frich et al. [30] investigated the subchondral bone thickness and found an average value of 1.9 mm (range of 1.2 to 2.9 mm). This result is analogous to the random examinations of subchondral bone thickness at various locations before the bone resection. Thus, the subchondral bone thickness of the 3D model is realistic and anatomically correct. A detailed study on this issue has not yet been conducted and might be the subject of future work using multiple shoulder models. Furthermore, this would support a generalisation of the results in comparison to using just a single shoulder model.

In the centric load case, the mean Von Mises stress values at the scapula clearly exhibit a decreasing behaviour with increasing implant depth. Due to the reaming procedure, the subchondral bone in the reference model is thinned and a mechanically fragile layer is obtained at the glenoid centre. Although this layer is still able to absorb a certain amount of stress, the layer obtained when the implant depth reaches 1.5 mm is no longer able to absorb any stress. At a depth of 1.5 mm, all of the subchondral bone is resected, and the bone cement layer is mainly in contact with the trabecular part of the glenoid. Only some regions at the glenoid rim provide contact with cortical bone. The analysis of the von Mises stresses demonstrates that a strength decrease, as reported by a previous study, cannot be directly inferred. Furthermore, the presented results are not directly comparable, because mechanical testing of pristine specimens was performed. However, a strength decrease of 25%, which can occur after resection of a bone depth of 1.0 mm, has been reported [9].

A clear increase in the stress values within bone cement was observed, and this increase is due to the lack of stability provided by the underlying bone. Only the bone cement coinciding with the glenoid rim has some contact with cortical bone. The rest of the bone cement has underlying trabecular bone with a weaker stability. The application of a centric load forces the implant to bend, which causes a higher stress within the implant and the bone cement. This effect increases with an eccentric load, which is represented by the higher stress difference that was obtained within the bone cement in comparison to the centric load. PMMA shows a high compressive yield strength of approximately 100 MPa, but a rather low tensile yield strength of 30 MPa [31]. The maximum tensile stress increased by 21.5% for the centric load and by 37.1% for the eccentric load. In each case, the maximum tensile and compressive strengths were not attained. Nevertheless, a higher load during daily activities can easily exceed the maximum tensile strength of bone cement, as has been reported [21]. Considering these higher forces, it can be concluded that bone cement is subject to a higher fatigue crack probability with increasing implant depth, due to the increased resection of subchondral bone. Subsequently, this effect results in an increased early fatigue failure risk of the bone cement layer and therefore potential implant loosening.

The interface between bone and cement is of major importance for load transmission and thereby, friction an important parameter which represents surface roughness. Ramaniraka et al. [24] investigated the influence of the friction coefficient at the bone–cement interface of a femur implant, showing that peak stresses (compressive and shear) remained almost constant for μ = 0.4 to 1.0. A natural conclusion is that changing the friction coefficient in our simulations would not alter the presented results critically and the assumption of μ = 0.6 is appropriate.

The observed micromotions at the interface between the scapula and bone cement indicate an adverse impact. The tangential micromotions (slipping) increased remarkably by 17.7 and 23.8% at an implant depth of 1.0 mm with respect to the reference model for the centric and eccentric load cases, respectively. In contrast, the normal micromotions (debonding) exhibited a decreasing behaviour with little difference between the centric and the eccentric load cases. An increasing implant depth contributes to a decrease in gap formation. This effect has not been previously observed and a further detailed investigation is necessary in order to fully explain this specific behaviour. Nevertheless, the decrease occurs less distinctively than the increase in tangential micromotions. The maximum increases reached in this study for the mean micromotions and the maximum micromotions were 28.0 and 30.2%, respectively, at the 2.0 mm implant depth. These results are lower than the values reported by Suárez et al. [6], who used FEA and found a 50% increase in micromotions at an implant depth of 3.0 mm compared with the optimal implant position. However, there was no differentiation between tangential and normal micromotions. The lower values obtained in this study can be explained by the use of a cemented implant instead of a cementless implant, as was used by Suárez et al. [6].

It must be emphasised that there is no coherency between the increases in the von Mises stress at the scapula in the different load cases and the tangential micromotions, because these are slightly lower for the eccentric load case. In contrast, the normal micromotions exhibit only minor differences. It is obvious that the friction coefficient influences the behaviour of the bone–PMMA interface. The opposed behaviour of tangential and normal micromotions seems peculiar at first glance, but is confirmable by previous studies, where this phenomenon was proposed as a biomechanical process promoting early failure of the bone–cement interface [24].

The magnitude of micromotions derived from the simulations in this study is very low, with a chance of just being numerical artefacts. Nevertheless, the values are within the magnitude found in the literature [6, 8]. Additionally, the final FE models were solved several times before the actual data analysis, to eliminate the possibility of numerical noise and ensure value stability and repeatability of the simulations.

To date, no study has directly quantified the relationship between micromotions and bone formation or resorption in humans. Bone formation has been observed in dogs with micromotions of less than 40 μm, whereas micromotions higher than 100 μm lead to the generation of fibrous tissue only [31]. In fact, the interface micromotions must be minimised for proper osteogenesis and bone ingrowth [32, 33].

Using a single patient’s FEA poses a limitation to this study, as a higher number of patients would substantially increase validity and transferability of the results. The abandonment of a full muscular model, using instead a simple centric and eccentric force application is a further limitation, but due to the effort and numerical stability, a necessary step of simplification. Nevertheless, substantial insight into the mechanical behaviour under consideration of implant depth has been provided.

Conclusion

The substantial increase in micromotions with progressive implant depth found in this study leads to serious concerns regarding long-term stability of the interface with an implant placed after excessive reaming. Furthermore, implant depth has a substantial influence on the stress distributions within bone cement. The fatigue stress of bone cement is more likely to be exceeded at higher implant depths, and higher micromotions could contribute to bone resorption and early implant failure in the long term. This study has clearly confirmed the general surgical guideline of subchondral bone preservation and found that minimisation of implant depth results in improved long-term survival.