Introduction

The results of China’s ninth forest resources inventory show that the total volumes of Larix olgensis A. Henry, Pinus sylvestris var. mongolica Litv. and Pinus koraiensis Siebold & Zucc. plantations in Heilongjiang Province were 79.7, 16.6 and 16.2 million m3, respectively, accounting for 33.6%, 53.6% and 61.3% of the national growing stock of these species in plantations. These conifers are the main species in northeast China in terms of economic return, timber supply and cone production (Jin et al. 2019).

The structure of the stand is an important component in forest inventory and management planning. Diameter distribution models have been widely used (Pogoda et al. 2019; Sun et al. 2019) because they provide a link between stand and individual tree models. Improving the prediction accuracy of these is an important research subject in forest inventory and management.

The probability density function (PDF) of a distribution is a continuous function defined by parameters, which do not always have biological interpretation (Zhang et al. 2003). From a practical perspective, PDF distributes stand attributes over a range of diameters to characterize the forest. An ideal PDF presents various distribution shapes encountered in forest stands. Johnson’s SB, Normal, Log-logistic, Gamma and Beta distribution have been applied for characterizing diameter distributions of trees (Hafley and Schreuder 1977; Rennolls and Wang 2005; Fonseca et al. 2009; Duan et al. 2013; Egonmwan and Ogana 2020; Gorgoso-Varela et al. 2020). Since Bailey and Dell (1973) first introduced the Weibull function, it has become accepted for predicting size distributions of conifers (Cao 2004; Newton and Amponsah 2005; Siipilehto et al. 2007). The advantage of the Weibull distribution is the strong correlation of its parameters with stand properties and the flexibility in modelling diameter distributions that have a single peak (Sghaier et al. 2016), a common shape in even-aged coniferous stands (Palahí et al. 2007).

Weibull distribution parameters have been predicted using parameter prediction methods (PPM) (Abino et al. 2016; Özçelik et al. 2016) and various parameter recovery methods (PRM) (Leduc et al. 2001; Liu et al. 2004; Burkhart and Tomé 2012). Ordinary least squares (OLS) and seemingly unrelated regression (SUR) analysis have been used to estimate the coefficients of the parameter prediction models (Zellner 1962; Siipilehto et al. 2007; Poudel and Cao 2013). PRM are often based on the estimates of certain percentiles or moments, and therefore their main source of error may be the inaccuracy of these point values (Poudel and Cao 2013). The results may vary depending on the combination of moments and percentiles used in the recovery (Siipilehto and Mehtätalo 2013). Using several diameter moments or percentiles to estimate the Weibull parameters can lead to over-parameterization.

The two-step PPM has frequently been used to predict diameter distributions of trees under different age of the tree stand, site characteristics, origin, mixing degree and management objective (Palahí et al. 2008; Sun et al. 2019; Schmidt et al. 2020; Waldy et al. 2022). The method first fits the distribution to a set of plots or stands and then uses the results to develop prediction models for the parameters of the distribution. However, no matter how accurately the first step in the PPM is conducted, the development of predictive models may be inadequate, leading to prediction errors (Parresol 2003; Fonseca et al. 2009).

In recent years, one-step parametric modelling techniques have been developed for diameter distribution functions. The maximum likelihood estimator regression (MLER) and the cumulative distribution function regression (CDFR) methods have received considerable attention. The former iteratively adjusts the coefficients of the parameter prediction models by maximizing the log-likelihood value calculated over all plots. The latter minimizes the sum of squared differences between the observed and predicted cumulative distribution probabilities to find the optimal coefficients of the parameter prediction models (Cao 2004). The CDFR has been superior to MLER and other methods in plantations of Picea mariana (Mill.) Britton, Sterns & Poggenburg, Pinus banksiana Lamb. in Canada, and Pinus taeda L. in the southern United States (Newton and Amponsah 2005; Cao and McCarty 2006).

A modified CDFR approach calculates the Weibull cumulative density function (CDF) using diameter class data instead of individual tree data (Poudel and Cao 2013). The modified CDFR method produced better results than the CDFR of Cao (2004) and other tested recovery methods in young Pinus taeda L. stands. In uneven-aged pine-oak mixtures (Pinus tabulaeformis Carr., Pinus armandii Franch. and Quercus aliena var. acuteserrata), CDFR was superior to both MLER and modified CDFR (Sun et al. 2019). In Schmidt et al. (2020), a linearized modified CDFR approach had larger errors than the other PPM and PRM approaches in predicting the diameter distributions of young Eucalyptus clonal stands in Brazil. The percentile-based parameter recovery method outperformed CDFR in young Pinus palustris Mill. plantations (Jiang and Brooks 2009). Nord-Larsen and Cao (2006) obtained relatively accurate results with the CDFR method in predicting the diameter distribution of European beech, Fagus sylvatica L., but the method was judged to be applicable only to young stands. Although MLER is a straightforward parametric method, it has rarely been applied to coniferous forests.

Previous studies have demonstrated that existing modelling methods and new parametric modelling methods give inconsistent results when applied to different areas and species. Despite the importance of L. olgensis, Pinus sylvestris and Pinus koraiensis in China, few diameter distribution models representing all the Heilongjiang region are available for forest management and planning. Model development has been hindered because permanent plots and silvicultural experiments were not designed for modelling purposes (Jin et al. 2019). Published models are often targeted to small geographic areas, specific species and stand structures, thus limiting their wider applicability. In diameter distribution modelling, the selection of the most appropriate approach based on a particular type of dataset remains a crucial issue (Hao et al. 2022). There is no clear rationale that would justify the superiority of one particular approach over the others (Cao 2004; Palahí et al. 2006).

Based on the above, diameter distribution modelling for the major coniferous stands in Heilongjiang requires further analyses. Although various parametric models have been reported, their applicability may be limited. The aim of this study was to compare three modelling approaches for predicting the diameter distributions of L. olgensis, Pinus sylvestris and Pinus koraiensis plantations in Heilongjiang based on the Weibull function. The other objective was to provide updated parameter prediction models for these species.

Materials and methods

Materials

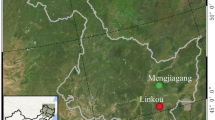
Data were collected in L. olgensis, Pinus sylvestris and Pinus koraiensis plantations in five locations in Heilongjiang Province (Harbin, Jiamusi, Mudanjiang, Yichun and Qitaihe). The plantations were located between 127° 18′ 00″ and 130° 52′ 36″ E, and 44° 27′ 40″ to 47° 24′ 00″ N and are mainly on gentle mountain slopes and low-elevation hills, with altitudes of 141–528 m. Sampling sites were located throughout most of the province, covering a wide range of sites and different geographical conditions (Fig. 1).

Fig. 1
figure 1

Study area and location of sampling points

Full size image

Sample plots from 21 forest farms were measured in the plantations with the dominant species of L. olgensis, Pinus sylvestris and Pinus koraiensis. The share of the dominant species was at least 75% of the total basal area (Zhang et al. 2003). The plots were randomly placed in various locations of the forest farms, excluding large gaps and gullies, and were rectangular fixed-area plots ranging from 0.04 to 0.16 ha. In each plot, diameters of all trees were measured at breast height of 1.3 m. The smallest diameter was 1 cm. The data of L. olgensis included 251 plots, of which 52 had been thinned and P. sylvestris included 169 plots, of which 42 had been thinned. A total 332 plots were measured in Pinus koraiensis plantations, including 97 thinned plots. The plots of all three species revealed different stand ages, site qualities, and terrain conditions (Table 1). The age groups used in the analyses is provided in Table 2.

Table 1 Statistical information of the research plots for the three species
Full size table
Table 2 Age classes used in the analyses
Full size table

Fitting diameter distributions

The two-parameter Weibull function was used to describe the diameter distributions. The probability density function of the two-parameter Weibull distribution is (Bailey and Dell 1973) (Eq. 1):

$$f\left(d\right)=\left(\frac{c}{b}\right){\left(\frac{d}{b}\right)}^{c-1}\mathrm{exp}\left[-{\left(\frac{d}{b}\right)}^{c}\right]$$
(1)

where d is diameter at breast height, b the scale parameter and c the shape parameter. The following maximum likelihood function was used to estimate the Weibull parameters b and c (Rennolls et al. 1985; Siipilehto 1999) (Eq. 2):

$$\mathrm{ln}L=\left(c-1\right)\sum\limits_{j=1}^{n}{p}_{j}\mathrm{ln}\left({d}_{j}\right)-P\left(c-1\right)\mathrm{ln}\left(b\right)+P\mathrm{ln}\left(\frac{c}{b}\right)-\sum\limits_{j=1}^{n}{p}_{j}{\left(\frac{{d}_{j}}{b}\right)}^{c}$$
(2)

where L is the likelihood function, \({p}_{j}\) the frequency of tree j, and P the total frequency of trees.

Modelling distribution parameters

The stand age, quadratic mean diameter, dominant height, number of trees per ha and basal area were used as explanatory variables in the prediction models. In addition, location variables such as elevation, aspect and slope were also considered as potential predictors.

Three different methods were used to develop the models: ordinary least squares (OLS), cumulative distribution function regression (CDFR) and maximum likelihood estimator regression (MLER). The latter two methods were implemented using SAS NLIN PROC. SAS codes for the required calculations are provided in the appendix of Cao (2004).

Ordinary least squares

After fitting the distribution function for each plot, the regression models for the Weibull parameters were developed using ordinary least squares. Parameter c was log-transformed to linearize the relationships and reduce heteroscedasticity. Stepwise regression was used to search for useful predictor combinations. All predictors had to be significant at the t-test 0.05 level, and the model had to be unbiased. The best model was selected based on Akaike information criterion (AIC). The basic forms of the parameter prediction models were also used in the CDFR and MLER methods.

Cumulative distribution function regression

The CDFR method used the following objective function to minimize the mean value of the squared differences between observed and predicted cumulative distribution probabilities in the modeling dataset (Eq. 3):

$$Min\frac{\sum_{i=1}^{n}\sum_{j=1}^{{n}_{i}}{\left({F}_{ij}-{\widehat{F}}_{ij}\right)}^{2}}{{n}_{i}}$$
(3)

where \({F}_{ij}\) is the observed cumulative probability for tree j in plot i, \({\widehat{F}}_{ij}\) the predicted cumulative probability at \({d}_{ij}\) (\({d}_{ij}\) is the diameter of tree j in plot i), n the number of sample plots, and \({n}_{i}\) the number of trees in plot i.

The coefficients of the parameter prediction models were optimized using the Newton algorithm (Cao 2004). The functional forms of the models for parameters b and c were obtained from the OLS method. The cumulative distribution function of two-parameter Weibull distribution is (Eq. 4):

$${\widehat{F}}_{ij}=1-\mathrm{exp}\left[{-\left(\frac{{d}_{ij}}{{b}_{i}}\right)}^{{c}_{i}}\right]$$
(4)

Maximum likelihood estimator regression

The MLER method is an optimization approach to the maximum likelihood estimation, which maximizes the sum of the log-likelihood values of all plots when the Weibull parameters are predicted with models (Cao 2004). The estimation procedure iteratively searches for the optimal values of the coefficients of the prediction models for parameters b and c. The objective function is (Eqs. 5 and 6):

$$Max\sum\limits_{i=1}^{n}\frac{\mathrm{ln}{L}_{i}}{{n}_{i}}$$
(5)
$$\mathrm{ln}{L}_{i}=\sum\limits_{j=1}^{{n}_{i}}\left[\mathrm{ln}{c}_{i}-\mathrm{ln}{b}_{i}+\left({c}_{i}-1\right)\mathrm{ln}\left(\frac{{d}_{ij}}{{b}_{i}}\right)-{\left(\frac{{d}_{ij}}{{b}_{i}}\right)}^{{c}_{i}}\right]$$
(6)

where n is the total number of plots, \(\mathrm{ln}{L}_{i}\) the log-likelihood value of plot i, \({n}_{i}\) the number of trees in plot i, and \({d}_{ij}\) the diameter of tree j in plot i.

Evaluation and validation

All plots of the three species were used in model fitting and the three methods were compared using the adjusted coefficient of determination (\({R}_{a}^{2}\)) and root mean square error (RMSE). K-fold cross-validation was used to evaluate the predictive performance of the models. The dataset was divided into k sub-samples. Each set of k-1 samples was used in modeling while the remaining one sub-sample was used for prediction and validation (Hastie et al. 2009). The average prediction performance of the method within the k samples was recorded.

Three other goodness-of-fit statistics were calculated for each combination of tree species and parameter prediction method: the one-sample Kolmogorov–Smirnov (KS) statistic, the Anderson–Darling (AD) statistic, and the Reynolds error-index (EI). The KS and AD statistics measured the agreement between the observed and estimated frequencies of trees. The predicted distributions were scaled to agree with the recorded total number of trees (Palahí et al. 2007).

The KS statistic evaluates the fitting performance of the models by measuring the maximum absolute distance between the given empirical CDF and the predicted CDF (Gorgoso-Varela et al. 2021). The KS statistics for plot i was calculated (Massey 1951) as follows (Eqs. 7 and 8):

$${KS}_{i}=\mathrm{max}\left\{{\mathrm{max}}_{1\le j\le {n}_{i}}\left[\left(j/{n}_{i}\right)-{\widehat{F}}_{ij}\right], {\mathrm{max}}_{1\le j\le {n}_{i}}\left[\left({\widehat{F}}_{ij}-\left(j-1\right)\right)/{n}_{i}\right]\right\}$$
(7)
$${\widehat{F}}_{ij}=1-\mathrm{exp}\left[-{\left(\frac{{d}_{ij}}{{b}_{i}}\right)}^{{c}_{i}}\right]$$
(8)

where \({\widehat{F}}_{ij}\) is the predicted cumulative distribution frequency of tree j, \({n}_{i}\) the number of trees in plot i, and \({d}_{ij}\) the diameter of tree j in plot i. In the calculation, trees are ordered into ascending order according to diameter.

Compared to KS, the AD statistic places more weight to the tails of the distribution. Opposite to KS, AD considers all points of the distribution, not only the point that gives the maximum difference. After sorting the diameters in ascending order, the AD statistic was computed using the following equation (Anderson and Darling 1954) (Eq. 9):

$${AD}_{i}=-{n}_{i}-\sum_{j=1}^{{n}_{i}}\frac{\left(2j-1\right)\left[\mathrm{ln}{\widehat{F}}_{\mathit{ij}}+\mathrm{ln}\left(1-{\widehat{F}}_{{n}_{i}-j+1}\right)\right]}{{n}_{i}}$$
(9)

The error index of Reynolds et al. (1988) calculates the total difference between predicted and observed number of trees in different diameter classes (Pogoda et al. 2019). It was calculated as follows (Reynolds et al. 1988) (Eq. 10):

$${EI}_{i}=\sum\limits_{k=1}^{{m}_{i}}\left|{n}_{ki}-{\widehat{n}}_{ki}\right|$$
(10)

where \({m}_{i}\) is the total number of diameter classes in plot i, \({n}_{ki}\) and \({\widehat{n}}_{ki}\) are, respectively, the observed and predicted number of trees per ha in diameter class k of plot i. In addition, the distribution of the error index was calculated for different stand age classes and visualized with the boxplot diagram. Further, the relative errors of the prediction methods in 5-cm diameter classes were calculated and visualized using boxplot diagrams.

Results

Parameter prediction models

Quadratic mean diameter, dominant height, stand density (ind. ha−1) and basal area were significant predictors for Weibull parameters b and c with high t-values (p < 0.05). Elevation, slope, and aspect were not significant predictors. Parameter b was significantly influenced by the quadratic mean diameter (Tables 3, 4). Only one explanatory variable was required in the prediction model for parameter b for Pinus sylvestris (Table 4). All three methods provided similar coefficient estimates (Tables 5, 6).

Table 3 Weibull parameters b and c for each species
Full size table
Table 4 Regression equation form for Weibull parameters b and c for each species
Full size table
Table 5 Regression coefficients of models for Weibull parameters b for each species
Full size table
Table 6 Regression coefficients of models for \(\mathrm{ln}c\) for each species
Full size table

All models for parameter b had Ra2 > 0.9 with RMSE ranging from 0.100 to 1.241 (Table 7). The fit of the parameter c model was not as good as that of b (Ra2: 0.358–0.534, RMSE: 3.199–4.229). The differences in Ra2 and RMSE between different prediction models for parameter b were small, while there were more differences in the models for parameter c. For all species, MLER and CDFR provided better models than OLS (Table 7). Although the goodness-of-fit statistics were similar for MLER and CDFR, models fitted with the CDFR method consistently had the lowest RMSE values.

Table 7 Fitting statistics for the parameter prediction models
Full size table

Analysis of different modelling approaches

The parameter prediction models produced by the three methods did not reveal large differences (Figs. 2, 3 and 4) in distributions but all models underestimated the number of large trees in over-mature Pinus sylvestris stands (Fig. 3). Compared to OLS, distributions predicted with the MLER and CDFR models described the peaks of the diameter distributions of mature and over-mature stands better.

Fig. 2
figure 2

Examples of observed and predicted diameter distributions in different age groups of Larix olgensis. Note the differences in scale of y-axis

Full size image
Fig. 3
figure 3

Examples of observed and predicted diameter distributions in different age groups of Pinus sylvestris. Note the differences in scale of y-axis

Full size image
Fig. 4
figure 4

Examples of observed and predicted diameter distributions in different age groups of Pinus koraiensis. Note the differences in scale of y-axis

Full size image

For the three species, the OLS-based models produced the poorest values for the AD, KS, and EI statistics (Table 8). Compared to OLS, the improvements of the three statistics using MLER or CDFR ranged from 1.7% to 29.4%. The AD, KS and EI statistics were fairly similar for the three prediction methods in Pinus koraiensis, CDFR being slightly more accurate and reliable than the other methods. Compared to OLS, MLER and CDFR improved the prediction accuracy of diameter distributions in L. olgensis and Pinus sylvestris. CDFR consistently had the smallest error index and standard deviation.

Table 8 Means and standard deviations (in parentheses) of the evaluation statistics for the three parameter prediction methods, OLS, MLER and CDFR
Full size table

The error index tended to increase with age for all species, most clearly in L. olgensis (Fig. 5). The distributions of error index were similar for the age groups < 20, 21–30, and 31–40 years in P. sylvestris and P. koraiensis, but the predictions differed more in mature stands (41–60, 61–80 years). The mean values of error index were lower for MLER and CDFR compared to OLS, and the between-plot standard deviations were also smaller for the MLER and CDFR methods. The CDFR had the smallest variation in the error index, both in the total data and in each age group.

Fig. 5
figure 5

Distributions of error index by stand age class for the three models and species. The horizontal line shows the median, the box the range between lower and upper quartile, and the vertical line the entire range. Outliers are indicated with dots

Full size image

In all three models, the relative errors were smallest for small diameter classes. On average, the models underestimated the frequencies of large diameter classes (Fig. 6). The OLS had wider distributions of the relative error in the boxplots compared to the MLER and CDFR methods, especially in medium and large diameter classes. All models showed similar results for Pinus koraiensis. For Pinus sylvestris, the models underestimated the frequencies of 35–40 cm diameter classes and overestimated frequencies in diameter class 15–30 cm.

Fig. 6
figure 6

Boxplots comparing the distributions of mean relative error in predicting the number of trees for diameter classes using different methods. The vertical line shows the median, the box the range between lower and upper quartile, and the horizontal line the range of relative error distribution for each diameter class. Outliers are indicated with dots

Full size image

Discussion

In Heilongjiang Province of China, recent trends in growth modelling for coniferous species have seen the increased use of individual tree models (Jin et al. 2017; Peng et al. 2018). This is because stand-level models have limited ability to provide information on the variation in tree size, making it difficult to correctly predict the volumes of different timber assortments (Peng 2000; Weiskittel et al. 2011). Diameter distribution models provide information on the variation in tree size, which may be used to improve growth and yield estimates (Miguel et al. 2010).

Few comparisons between alternative modelling approaches to predict the diameter distributions of plantations are available in Heilongjiang. For example, the applicability of MLER and CDFR methods to the major coniferous species has not been previously examined. This study contributed information by evaluating the MLER and CDFR methods using the two-step PPM (OLS) as a benchmark. The evaluations were done for the most important conifer species of plantation forests. The plots for modeling were measured in different parts of the province and the data provided a good sample of different forest conditions.

The models developed in this study are for even-aged stands. If the species are grown in mixed stands, the models can be used in predicting the diameter distribution of the target species alone (Maltamo 1997) until models targeted specifically to mixed stands become available. Diameter distribution models can be used in combination with both individual tree and stand models, making it possible to develop different types of practical applications (Zhang and Lei 2010; Pogoda et al. 2019). Linking tree-wise models and stand-level data via diameter distribution models has become common in cases where only stand-level forest inventory data are available (Maltamo 1997; Trasobares et al. 2004; Pasalodos-Tato and Pukkala 2008; Pasalodos-Tato et al. 2016; Nunes et al. 2022).

The two-parameter Weibull function was used to fit the diameter distributions. Despite the differences in stand structure among the plots, the Weibull distribution provided an accurate representation of the stem frequency distribution (Palahí et al. 2007). Frugality is one of the aims in model development (Borders and Patterson 1990), and the two-parameter Weibull model is often sufficient to characterize one-peaked diameter distributions of trees (Bullock and Burkhart 2005). Besides, the two-parameter Weibull model avoids problems of obtaining non positive estimates for parameter a and convergence failures in fitting three-parameter distributions (Nord-Larsen and Cao 2006; Pogoda et al. 2019).

Weibull parameter b was more predictable than parameter c. The reason for the poor fit for c may be that available stand variables such as mean diameter and stand density are not ideal to successfully predict parameter c. The goodness of fit of the model for c has always been low (Little 1983; Cao 2004; Liu et al. 2004; Newton and Amponsah 2005). Even though attempts have been made to improve predictions using, for instance, skewness information or remotely sensed metrics, the results remain unsatisfactory (Lindsay et al. 1996; Hao et al. 2022). Based on graphical inspection (Figs. 2, 3 and 4), it seems that parameter c is better predicted in the CDFR and MLER methods, as they predict higher kurtosis in the distributions.

The methods tested best predicted the diameter distributions for stands younger than 40 years, confirming earlier findings that diameter distribution models tend to work best in young stands (Gobakken and Næsset 2004, 2005; Siipilehto 2011a, b). Mature and over-mature stands may have undergone natural thinning and harvesting, resulting in more complicated diameter distributions that are harder to predict (Tian et al. 2021; West 2021; Pukkala 2022). It has been found that using the maximum tree diameter or dominant height as a predictor improves the goodness-of-fit of the PPM (Siipilehto and Mehtätalo 2013; Goodwin 2021). In our data, dominant tree height was a significant predictor in some models, and using maximum diameter or certain diameter percentiles may have improved the models further. However, these additional variables are not necessarily available in forest inventory data.

The main objective of developing parameter prediction models is to obtain the best approximation of the size distribution of trees using available characteristics (Pogoda et al. 2019). The degree of prediction error at the diameter class level is an important factor (Newton and Amponsah 2005). If the errors are systematically large for certain diameter classes, the reliability of the model can be questionable, even if the predictions are accurate for most diameter classes (West 2021).

Data for different diameter classes also suggest that the two optimization-based methods produce better parameter predictions than the two-step regression method (Cao 2004; Palahí et al. 2006). The concept of both methods is the same as both optimize the coefficients of the parameter prediction models without first fitting the Weibull functions to the plot data and using the fitting results in a separate modelling step (Cao 2004). In the MLER and CDFR methods, the model forms were from the OLS analyses. This may have decreased the method performance compared to where the model forms are optimized simultaneously with the coefficients (Bankston et al. 2021).

Conclusion

This study developed models for predicting the diameter distributions of the major coniferous plantation species in Heilongjiang Province. The two-parameter Weibull distribution proved to be sufficiently flexible for describing diameter distributions of even-aged conifer plantations. The developed models predicted the diameter distribution parameters using quadratic mean diameter, dominant height, basal area, and number of trees per ha. In practice, representative trees can be extracted from the predicted distribution, and tree-wise growth models can then be used to simulate stand development (Palahí et al. 2006). In this way, the new diameter distribution models can be combined with existing tree-level models for diameter increment, survival, biomass, and stem taper (Dong et al. 2016; Jin et al. 2017). Of the three tested models, the CDFR outperformed the OLS and MLER. Therefore, it is suggested the CDFR method be used for developing models for predicting diameter distributions of coniferous plantations.