Abstract
The effects of drought on tree mortality at forest stands are not completely understood. For assessing their water supply, knowledge of the small-scale distribution of soil moisture as well as its temporal changes is a key issue in an era of climate change. However, traditional methods like taking soil samples or installing data loggers solely collect parameters of a single point or of a small soil volume. Electrical resistivity tomography (ERT) is a suitable method for monitoring soil moisture changes and has rarely been used in forests. This method was applied at two forest sites in Bavaria, Germany to obtain high-resolution data of temporal soil moisture variations. Geoelectrical measurements (2D and 3D) were conducted at both sites over several years (2015–2018/2020) and compared with soil moisture data (matric potential or volumetric water content) for the monitoring plots. The greatest variations in resistivity values that highly correlate with soil moisture data were found in the main rooting zone. Using the ERT data, temporal trends could be tracked in several dimensions, such as the interannual increase in the depth of influence from drought events and their duration, as well as rising resistivity values going along with decreasing soil moisture. The results reveal that resistivity changes are a good proxy for seasonal and interannual soil moisture variations. Therefore, 2D- and 3D-ERT are recommended as comparatively non-laborious methods for small-spatial scale monitoring of soil moisture changes in the main rooting zone and the underlying subsurface of forested sites. Higher spatial and temporal resolution allows a better understanding of the water supply for trees, especially in times of drought.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As a result of changing climate, many forest sites suffer from drought stress because of limited plant-available water. Consequently, many forest stands with an increased vulnerability either directly collapse or are no longer resilient to further sources of stress like insect infestations (Netherer et al. 2019). Sufficient plant-available water along with an adequate nutrient supply, are critical for vital, stable, and well-growing forest stands (Gracia et al. 1999; Mellert and Ewald 2014; Mellert et al. 2018). Despite their importance, the effects of drought on forests are still not fully understood (Etzold et al. 2014), especially when focused on small-scale subsurface heterogeneities (Schuldt et al. 2020).
For assessing the water supply of trees, knowledge of small-spatially distributed soil moisture, its availability and its temporal changes is a key issue. Monitoring water availability for vegetation remains difficult due to limited access to quantify soil moisture without disturbing the soil structure. For determining soil moisture content, there are traditional methods such as time domain reflectometry (TDR) probes (Evett 2003) or gravimetric methods (Van Reeuwijk 1992). However, these methods only collect data from a single point or from a small soil volume.
For this reason, electrical resistivity tomography (ERT) can be an alternative or complementary method to obtain information on soil moisture dynamics and its spatial distribution (Samouëlian et al. 2005; Brunet et al. 2010). ERT is a prominent method in geomorphology and soil science for characterizing the subsurface, for example in identifying sections with frozen ground (Kneisel et al. 2014, 2015) or groundwater depth and contamination (White 1988; Ahmed and Sulaiman 2001). It is also applied in geoengineering for surveying the conditions of embankments (Ikard et al. 2014; Norooz et al. 2021), in characterization of contaminated sites, and for monitoring soil remediation techniques (Nivorlis et al. 2019). Several studies have already shown the potential of repeated resistivity measurements for tracking root-zone moisture distribution in precision farming (e.g., Michot et al. 2003; Srayeddin and Doussan 2009). Jayawickreme et al. (2008), Nijland et al. (2010), and Carrière et al. (2020) used ERT on forest sites and quantified moisture content in the measured section of resistivity values by applying physical properties of the subsurface in accordance with Archie`s law (Archie 1942). Spatial anomalies are also driven by heterogeneous soil physics. Consequently, the derived values of ERT data should be treated with caution, especially regarding their spatial resolution. Therefore, ERT has not often been used in temperate forests since the field situations are quite complex and heterogeneous (due to tree roots), resulting in weaker relations between soil moisture and resistivity values compared to results from sites with more homogeneous soils like croplands and grasslands (Seladji et al. 2010). There are rather lab experiments under controlled conditions reporting very high correlations between resistivity values and volumetric soil water content (Werban et al. 2008; Hadzick et al. 2011). However, for a better understanding of the causal relationship between soil drought and the effects on stand vitality and growth, the use of spatially high-resolution two- or even three-dimensional models of soil moisture distribution offers valuable and innovative potential, since it delivers additional spatial insights into the interactions between the biosphere, hydrosphere, and atmosphere (Jayawickreme et al. 2008; Carrière et al. 2020).
As a minimally-invasive method, ERT does not require coring or other soil disturbances and can - depending on the electrode spacing - provide information down to a depth of several meters. Furthermore, measurements can be repeated with constant settings (De Jong et al. 2020) that allows the detection of changes in pedological properties of the explored subsurface. The electrical resistivity is driven by several soil parameters such as physical properties (e.g., texture or porosity), organic content and moisture. If the physical parameters and organic content remain constant through comparatively short observation periods (e.g., 5–10 years), variations in resistivity between repeated measurements can be attributed to soil moisture changes (Samouëlian et al. 2005).
To investigate this relationship over several years, two different forest sites in Lower Frankonia (Germany) with different lithologies were instrumented with geoelectrical monitoring and soil moisture sensors. In this study, we aim to evaluate weekly to monthly repeated ERT measurements as a promising method to detect temporal soil moisture changes by comparing the results to matric potential and volumetric water content in the subsurface of temperate forests.
Material and methods
Study sites
The study was focused on two dry regions with different lithologies and soil development in Lower Frankonia, a Bavarian government district in Germany (Fig. 1). One of the sites (WUE) was an existing forest monitoring plot in the “Guttenberger Wald” of the Bavarian Institute of Forestry (LWF) located in the southeastern cuesta region close to Würzburg (49°43'N, 09°53'E; 330 m a.s.l.) which is one of the driest forest sites in Bavaria. The WUE site is characterized by Cambisol/Luvisol soils from the Lower Keuper Formation, a subcontinental climate with mild winters, a mean annual air temperature of 9.6 °C and a mean annual precipitation of 601 mm (reference period for Würzburg: 1981–2010; DWD 2021). The forest consists of a main stand with oak (Quercus robur L.; approximately 105 years-old) as well as understory consisting of hornbeam (Carpinus betulus L.) and European beech (Fagus sylvatica L.).
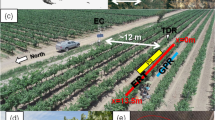
Overview for the two study sites: a shows a sketch map of the 3D-ERT grid at UHW is shown, whereas in b the locations of the two study sites are marked on a digital elevation model (DEM 25 m, LDBV 2021) of Lower Frankonia (Germany). The sketch map of WUE is shown in c. The cover by tree crowns in a and c is not true to scale
The second study site is located in the “Unterhübnerwald” (UHW) in the Lower Main Plain close to Aschaffenburg (49°59 ‘N, 09°1’E, 126 m a.s.l.) with Dystric Cambisol soils from eolian/alluvial sands and gravels. This site is characterized by a temperate warm climate with a mean annual air temperature of 10.0 °C and a precipitation of 648 mm (reference period for Schaafheim/Schlierbach: 1981–2010; DWD 2021). It is a mixed forest stocked with Scots pine (Pinus sylvestris L. approximately 140 years-old), European beech (Fagus sylvatica; approximately 30 years-old) and Norway Spruce (Picea abies L.; approximately 120 years-old).
Electrical resistivity tomography (ERT)
ERT is a minimally invasive method to measure the spatial distribution of electrical resistivity in the subsurface. Since different geomaterials like clay, sand, or rock, but also water and air are each characterized by a specific electrical resistivity, the method enables a delineation of different materials. If the composition of the existing substrate/rock does not temporally change, except for air and water content, changes in electrical resistivity can be primarily attributed to these changes. Therefore, ERT is well-suited to investigate small-scale variations of water content in the subsurface on a spatial and temporal scale.
To measure the electrical resistivity, several stainless-steel pins, serving as electrodes, are placed in the topsoil at a defined spacing along a horizontal transect line. All electrodes are linked by a multi-core cable connected to a control device. Out of at least four required electrodes, two (current electrodes A & B) are used to inject a known current into the ground, and the other two (potential electrodes M & N) allow the measurement of the resulting potential difference within the subsurface. Using Ohm's law, an apparent resistivity can be calculated via the known current (I), the measured potential difference (ΔV) and a geometry-dependent correction factor k (Eq. 1; e.g., Kneisel and Hauck 2008; Reynolds 2011). The calculated apparent resistivity is the resistivity of a half-space which produces the observed potential measured by a particular electrode geometry. The apparent resistivity is equal to the specific resistivity of the explored subsurface only if it is characterized by a uniform half-space (Reynolds 2011). The factor k depends on the arrangement of the four electrodes (Kneisel and Hauck 2008) and is calculated by the distance (spacing) of four certain electrode combinations (Eq. 2; Reynolds 2011).
The electrode spacing defines the exploration depth, i.e., the greater the spacing, the deeper the quadrupole measured by the respective electrodes (cf. Fig. 2). Using numerous electrodes connected to a multi-core cable along a transect, several hundreds of quadrupoles can be measured, delivering a 2D resistivity cross section—a so-called pseudo-section—of the subsurface. Regarding the arrangement of the current and potential electrodes, there are different array types. The Wenner-Schlumberger and the dipole–dipole array used in this study are shown in Fig. 2. The Wenner-Schlumberger array is characterized by good vertical and horizontal resolution as well as a high signal-to-noise ratio. The dipole–dipole array is very sensitive to lateral changes due to a higher point density, especially in the near-surface area, but is characterized by a lower signal-to-noise ratio and is therefore more susceptible to non-ideal conditions such as poor electrode coupling (Loke 2004).
At the WUE plot, a 2D-ERT transect was installed by inserting 36 electrodes at 1-m spacing over 35 m. Along this transect, there was a marked difference in the density of adjacent trees, with a higher density in the first half (E1-E14; Fig. 1) and lower density in the second (E15-E36). Since May 2015, measurements with a Wenner-Schlumberger array were performed almost weekly, delivering resistivity values with a total of 288 quadrupoles.
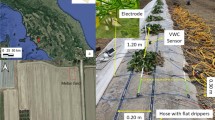
By changing the electrode arrangement from a single line to a two-dimensional grid ensuring the same spacing between every electrode, even more combinations (also diagonal electrode arrays) are possible for resistivity measurements, resulting in a 3D resistivity section of the explored subsurface. This was applied at the UHW site and consisted of 8 × 9 electrodes at 1-m spacing, resulting in a 7 m × 8 m grid. Due to the smaller and compact electrode arrangement, a dipole–dipole array was used because of its higher sensitivity to lateral changes. The respective array with a total of 750 quadrupoles was measured between December 2014 and May 2018. Sites with the most homogeneous soil conditions in both areas were selected as locations for the ERT profile and grid.
ERT data was collected at both sites using the IRIS Syscal Pro Switch & Syscal Junior resistivity imaging system. After the measurement with 2–4 stacks (measurement replicates per quadrupole), a quality check with a maximum of 5% stack deviation was carried out according to Loke (2004). For interpreting spatial differences in resistivity values, the raw 2D- and 3D-ERT data were inverted using the software BERT v.2.3.0, according to Günther et al. (2006) and Rücker et al. (2006). In this course, pseudo-sections were derived from resistivity values measured for each quadrupole by solving the inverse problem to realize a visual illustration. A robust inversion constraint was used, which produces sharp boundaries between different areas of homogenous resistivity distributions. During the iterative inversion process, the program attempts to model a resistivity distribution that can best explain the resistivity values in the subsurface. The deviation of the modeled resistivity distribution from the measured values is then expressed as a root-mean-square (RMS) error. For better comparability, an additional timelapse inversion was carried out, visualizing the ratio of resistivity change between selected measurement dates.
Owing to a high variance of resistivity values ending in a non-normally distributed data collective per depth layer at the study site UHW, the median was used instead of the mean (cf. WUE) when averaged values were necessary for further data processing (cf. correlation with pF value, time-depth profile).
Derivation of meteorological data
To evaluate the resistivity measurements for their applicability in detection of soil moisture changes, soil moisture content measured by the LWF was received for the study period at the WUE site. The soil moisture content was measured every half-hour by TDR-probes at depths from 5 to 110 cm with a vertical spacing of 10 cm and one to five replicates per depth. At the UHW site, a Tensiomark-Soil-System (GeoPrecision GmbH) was installed for surveying the soil matric potential hourly at 75 cm depth. Climate data was also obtained from the nearest weather station of the DWD (UHW: Schaafheim/Schlierbach; WUE: Würzburg).
Results and interpretation
The meteorological data of the two sites are of considerable importance for the interpretation of the temporal and spatial changes in the geophysical data sets. Figure 3 provides an overview of the precipitation and soil moisture development in the main rooting zone of the two sites over the study period. With regard to the temporal precipitation distribution, there is no clear rainy season. However, seasonal changes become apparent through the soil moisture variation, with the driest values (low water content; high pF value) during the growing season compared to the entire measurement period. The driest soil moisture values and least precipitations were found during the growing season in 2018 which was, together with 2015, one of the years with the driest summer for forest sites in Europe/Germany (Ionita et al. 2017; Schuldt et al. 2020). The data in Fig. 3 will be used for interpretation and discussion in the following sections.
2D ERT (WUE)
The raw resistivity values from the 2D-ERT measurements at WUE were between 20 and 270 Ωm, in the range of the specific resistivity of clay according to Reynolds (2011) and Knödel et al. (2013). The two-dimensional profile at WUE (Fig. 4) is characterized by a two-layered structure consisting of an upper 1.5 m layer with seasonally fluctuating resistivity values (15–300 Ωm) and a second 1.5–4 m layer with more constant values (40–100 Ωm).
Figure 4 shows the seasonal changes of the resistivity distribution in the subsurface along the profile. Between the tomograms, preferably dated close to the beginning of a hydrological half-year (November 1; May 1), there is always a clear reduction or an increase of the resistivity values in the subsurface. This is indicated by a timelapse ratio at the right column of Fig. 4, with red model cells indicating an increase in resistivity (drying) and blue showing a decrease (wetting).
The constantly higher resistivity values in the uppermost layer between E1 and E14 compared to the values from E15 to E36 (Fig. 4) can be explained by the higher stand density at the side of the ERT-profile (cf. Fig. 1). This is due to the higher specific resistivity of tree roots (300–1200 Ωm; Bieker and Rust 2010) compared to clay, and a lower moisture content due to increased water consumption in the main rooting zone during the growing season in this half of the pseudo-section. The underlying low-resistivity section (> 1.5 m depth) may not be decisively influenced by the trees like the above-mentioned model cells. Because of temporally constant resistivity values, the deeper part in the middle of the pseudo-section (Fig. 4: 18–24 m) may be shaped by the presence of bedrock. In contrast to seasonally changing low-resistivity values of the surrounding model blocks at the same depths, this high-resistivity part in the middle seems to be characterized by a lower water infiltration, resulting in interannually rising resistivity values (constantly light red section in the timelapse tomograms).
To make the short-term changes in resistivity visible for all the measurement dates, Fig. 5 shows averaged values by depth and measurement date as a time-depth profile with hydrological half-years indicated.
As seen in Fig. 4, the upper layers vary considerably more than the deeper layers and include both the lowest and highest resistivity in the entire time-depth profile. Regarding absolute values, the dark blue sections with a resistivity of < 30 Ωm correspond to moist clay or at least moist, clay-rich soils (Reynolds 2011), and indicate the moist periods, beginning in the middle of the hydrological winter half years. This is shown by the rising soil water content in the main rooting zone during winter and spring (Fig. 3). In contrast, the upper layers are characterized by resistivity values > 65 Ωm during some periods (in the range of dry clay according to Reynolds 2011), which are associated with a drop of soil moisture in the effective root area. These time sections are shaped by dry periods beginning at the middle of the hydrological summer half-year. Conspicuous is the different time delay of the wetting and drying process in the soil along the upper three meters. While moisture penetration progresses comparatively slowly and continuously in winter, desiccation begins abruptly in the upper three meters of the measurement profile in summer. The seasonally changing resistivity is also detectable in the deeper layers, but weakened (compared to the time-varying resistivity values in the upper 3-m depth), which is possibly related to another substrate and the presence of bedrock, respectively (cf. interpretation for Fig. 4 at that depth). However, dry periods also occurred in the deeper half of the ERT-probing depth (3–6 m), especially in the last three years (2018, 2019, 2020). Even if these depths are less relevant for the direct water supply for trees, the temporally increasing resistivity values, accompanied by an interannual decrease in water content in the main rooting zone, should be still considered. This matches the results in the resistivity ratios in Fig. 4, showing a stronger increase (up to factor 10) than the decrease (up to factor 0.4) of resistivity to the next half-year, which causes a cumulative long-term effect of desiccation. In conclusion, the interannual strengthening of the drought periods indicated by increasing resistivity values goes along with a weakening of the moist periods along all depth levels.
Since the TDR-probes of the LWF detect soil moisture only in the main rooting zone (< 1 m), a direct correlation was possible only between the mean of the upper two data points of the ERT pseudo-sections (depths: 0.52 cm, 0.92 cm), and the average of all moisture probes for the respective measurement day, presented as a regression model in Fig. 6. However, the good correlation between the means of these parameters underlines the above interpretation of the resistivity data, considering inter- and intra-seasonal changes of soil moisture.
3D ERT (UHW)
The ERT measurements at the UHW site delivered a 3D subsurface model (Fig. 7), which is also characterized by a two-layered structure. Compared to the WUE site, the delineation of the two layers is more distinct and the uppermost 2-m layer is characterized by higher electrical resistivity than the deeper layers (2–4 m). The resistivity values in the upper layer vary between 500 and several tens of thousands Ωm, whereas the resistivity of the deeper layer remains more constant below 500 Ωm. This range in the upper layers seems to be quite large, (compared to the range of resistivity values measured at the WUE site) but should be expected for the eolian/alluvial sand and gravel substrates present with varying moisture contents (cf. Reynolds 2011). A continuous low-resistivity anomaly is conspicuous in the subsurface (turquoise/blue cells) of the model, which corresponds to the location of a Scots pine (Figs. 1 and 7, y: 7 m, x: 3 m) and a Norway spruce (Figs. 1 and 7, y: 4 m, x: 2 m) within the grid.
The 3D-tomogramms in Fig. 7 also reveal the seasonal change of the specific resistivity in the subsurface of the grid. The 3D-ratio models (right column) highlight the afore mentioned two layers with different patterns of resistivity change, whereby the upper layer alternates seasonally between an increase and a decrease of resistivity values. In contrast, the deeper layer continuously showed a slightly decreasing resistivity in sandy soil throughout the entire period (ratio < 1). At the location of the trees within the grid, the ratio between the different time steps remained unaffected and reacts, considering the timestep ratio, similarly to the resistivity values of neighboring cells.
Compared to the 2D-ERT results for the WUE site, the time-depth profile for UHW (Fig. 8) shows the reversed vertical pattern mentioned above with the highest resistivity values in the upper 1.5 m (main rooting zone) and the lowest in the deeper part of the exploration depth. The high-resistivity sections (red) in 2015 extend comparatively widely both vertically and along the time span which is in line with the severe drought in Germany/Europe during the 2015 growing season (Ionita et al. 2017). This is supported by low rainfall and continuously rising pF values (Figs. 3 and 8). However, there were higher pF values in 2016 and 2017 but with high, short-term fluctuation. Due to the high density of measurement dates from June 2016 to July 2017, the unsteadiness of pF values can be confirmed based on ERT data for this period. Figure 9 also shows a high correlation between the pF value at 75 cm depth and the median resistivity of the quadrupoles at 69 cm depth.
Discussion
Seasonal variations and interannual trends could be observed considering temporal resistivity changes at both sites. Half-yearly alternating drying, and wetting periods were detected using ERT, which was verified by soil moisture data from both study sites (Figs. 5 and 8). This pattern is consistent with the seasonally fluctuating evapotranspiration of temperate forests with a summer maximum and a winter minimum (Oishi et al. 2010). However, the spatial resistivity variations were opposed with respect to the vertical gradient, i.e., the lowest resistivities in the clayey soil at WUE were in the effective root zone (top half of the probing depth), while they were found below the effective root zone at UHW. This contrast is most likely due to the sand substrate which has lower water retention and higher drainage compared to clay. Plant available water during the humid periods is directly retained by the clayey soil (WUE site) during subsequent growing seasons with potential water deficits. Due to the exceedingly high water storage capacity of the topsoil, deeper layers do not receive any percolating water. Over several years, the water stored in the upper half of the exploration depth at WUE is successively used by the trees during the growing season. Therefore, no seepage water reaches the discharge horizons from the effective root zone into the deeper layers due to the scarcity of plant available water. Consequently, the deeper layers are not affected by seasonal or semi-annual fluctuations, but rather by the water balance in the topsoil. At the sandy UHW site, the situation is reversed, meaning that the topsoil stores a minimum amount of water and most of it seeps directly through the effective rooting zone in a very short time. The interpretations above are also supported by the temporal ratios of the 2D and 3D tomograms (Figs. 5 and 7). Accordingly, they show seasonal fluctuations of the resistivities in the near surface region (changing ratios between > 1 and < 1), which are accompanied by seasonal fluctuating soil moisture values (Figs. 4 and 6). In contrast, the deeper half of the ERT-probing does not show changing ratios between the respective half-years but an interannual trend, revealing a different tendency. The continuous temporal increase in resistivity per season is due to more severe and longer dry periods, resulting in a cumulative effect of desiccation in the deeper half of the subsurface at WUE and should have careful attention in the future.
Spatial anomalies due to trees
The high-resistivity anomalies in the WUE main rooting zone could be attributed to a higher tree density. In contrast, Norway spruce and Scots pine in the 3D-grid of the UHW site promoted low-resistivity model blocks compared to the surrounding sections. This contradiction is due to the higher resistivity ranges of sands compared to clay. Resistivity values of wood (300–1200 Ωm) lie between those measured at the WUE site (15–300 Ωm) and the resistivity values from the main rooting zone at UHW (500–60,000 Ωm), which justifies the different relations. However, there are further reasons for different resistivity values related to the presence of trees, like stem flow, promoting water supply close to the roots. This phenomenon can be very high and varies considerably, depending on species, crown geometry and size (Taniguchi et al. 1996; Návar 2011), resulting in high moisture values and consequently low resistivity values in the soil close to the trunk. Owing to its dependence on precipitation, this part of the water supply occurs for a short time and differs widely, depending on the season (with or without leaves). However, this parameter can be ignored in this study since only coarse barked trees (Scots pine, red oak, Norway spruce), whose stemflow are low or non-existent, formed the main stand. In contrast, seasonally varying water uptake by trees reduces moisture close to the trunk. This is shown by the high-resistivity sections in the ERT-profile at the end of the growing season for the WUE site (Fig. 4) characterized by a higher stand density. Since mature deciduous forests can contribute to groundwater fluctuations up to a depth of several meters due to their transpiration (Mitscherlich 1971), such resistivity anomalies can be attributed to different stand densities. Moreover, different degrees of water uptake depending on species are also possible. When comparing Norway spruce (Figs. 1 and, y: 4 m, x: 2 m) with Scots pine (Figs. 1 and 7, y: 7 m, x: 3 m) located in the 3D grid of UHW site, there is always a stronger low-resistivity anomaly around the pine than with the spruce, especially during the growing season. This matches the generally lower water use of a mature Scots pine compared to Norway spruce during the growing season (Schmidt-Vogt 1986). However, the situation is complicated by trees segregating root exudates seasonally for nutrient mobilization (Gerke 1992; Grayston et al.1997), thereby increasing the electrolyte content of the soil and consequently decreasing resistivity. Therefore, a quantitative assignment of certain tree parameters to the measured resistivity anomalies was not possible in this study. To investigate these anomalies in more detail, models with a higher resolution would have to be developed with the help of, for example, a smaller electrode spacing. However, temporal changes in resistivity values at the same location are still mainly driven by water content, even if the site is covered by trees (see Fig. 6).
Resistivity vs. soil moisture
The strongest resistivity anomalies as well as temporal variations reach down to approximately 1.0 m and 1.5 m depths, respectively, corresponding to the main rooting zones of both forest sites. The temporal variation of the resistivity values correlates well with the soil moisture changes down to 1 m depth (Fig. 6). Since mean or median values from single point measurements are also used in classical soil moisture estimations or for hydrological modelling in forest ecology, calibration of the spatial resistivity model with the help of the functional correlation obtained from mean soil moisture values is considered permissible, at least for the depth range considered in this process. However, this should be verified or corrected using pedotransfer functions (e.g., Archie 1942), incorporating soil physical parameters. Since the sole value of volumetric water content is not sufficient, the estimation of the corresponding soil matric potential would be another step towards a more accurate, two- or three-dimensional high-resolution determination of plant-available water in the effective rooting zone of trees. This could finally allow an estimation of tree-available water for determining critical time spans and even small-spatial soil sections with a limited water supply. Such progress would also be important in times of climate change, not least because the effects of drought on forest ecosystems are not fully understood due to small-scale heterogeneities (Etzold et al. 2014; Schuldt et al. 2020).
Methodological approach
Due to the influence of soil temperature in the subsurface (Hayley et al. 2010), a preliminary correction of the resistivity values would be necessary prior to quantitative derivations from resistivity data. Even though there is, according to Ma et al. (2014), no significant correlation between soil temperature and changing resistivity values in forest soils, the moisture values estimated by the apparent resistivity without a temperature correction would be overestimated in summer and underestimated in winter, resulting in an insufficiently stringent evaluation of the trees’ water supply. The fact that the results presented here were not corrected for temperature should be viewed critically, but this had no influence on our relational-qualitative observations and statements. Since dry seasons are characterized by high temperatures and wet periods are shaped by low temperatures in this region, the contrasts between these half-years (Figs. 5 and 8) would even be intensified with a temperature correction of the resistivity values. This is justified by the fact that rising temperatures in the subsurface affect a lowering of its resistivity (Besson et al. 2008; Reynolds 2011).
The electrode arrays selected were based on the respective site characteristics and the measurement set-up. At the WUE site, the more stable, robust, and therefore better suited for monitoring Wenner-Schlumberger array (Furmann et al. 2003; Loke 2004) was used. The data sets show high quality and only low error values over the measurement period (cf. Fig. 4). Individual data sets with larger errors were caused exclusively by minor defects of the cable, which could be limited to short periods by repair or replacement. The corresponding data sets were sorted out before processing. At the UHW site, the dipole–dipole array was used because of better lateral resolution within the comparatively small grid to better resolve the small-scale, three-dimensional variability (cf. Loke 2004). Due to the poorer signal-to-noise ratio and the higher susceptibility to poor ground coupling, the sandy substrate with strongly fluctuating moisture values does not seem to deliver the most suitable conditions for this type of array at this site. This is also reflected in the higher errors compared to the WUE site which, however, are still within an acceptable range. Figure 7 further illustrates horizontal imbalances. Despite generally visible chronological trends given by the 3D-models, there are neighboring model cells in blue and red delivering opposed ratios. Nevertheless, this contrast should not be overrated since the fluffy sand takes a wide span of resistivity values (Reynolds 2011), resulting in big differences even for neighboring model cells. This problem was also enhanced by the warm and very dry summer months when the sandy soil only allowed poor coupling of the electrodes. Nevertheless, in comparative measurements with the Wenner-Schlumberger array at this site, the dipole–dipole array resolved the small-scale variabilities significantly better and was therefore preferred at this site, despite the slightly higher error values.
ERT in forest ecosystem monitoring and outlook
Based on our results, ERT offers great potential in monitoring soil moisture changes at forest sites and at a small scale. As a minimally invasive geophysical method, ERT-measurements do not disturb the soil system and are quickly established. Sampling for estimating gravimetric water content or for installing TDR-probes is considerably more complicated, time-consuming, and costly. Furthermore, they provide limited spatial and temporal resolution, which are both offered by ERT monitoring. Figures 4, 5, 7 and 8 illustrate the importance of each additional dimension in resistivity changes, like the interannual increase of the degree of influence from dry periods and their duration as well as rising resistivity values as a result of decreasing soil moisture driven by the forest stand itself. A higher spatial and temporal resolution in soil moisture distribution particularly offers a better understanding of the water supply for trees in times of dry growing seasons, which is becoming more important.
Nevertheless, for producing quantitative soil moisture values from measured resistivity values (cf. Ma et al. 2014), a site- related calibration with installed in-situ data loggers must be done, and pedotransfer functions (e.g., Archie 1942) should be applied. Soil conditions are to be assumed homogenous, which are rare in forests. The presence of stems and roots is the main driver for this pedological inhomogeneity, owing to their different specific resistivities compared to the surrounding substrate. For this reason, the use of both methods (pedotransfer functions and data logger calibration) is suggested for verifying the site-specific relationship between absolute soil moisture and resistivity values.
To provide evidence for plant-available soil water using resistivity values, it is important to regard both absolute water content and soil matric potential. Concerning forest sites, different sensor distances to the nearest tree should also be realized to ensure an additional view of the impact of roots on the substrate, water content and soil temperature. Such a combined consideration has not yet been addressed in respective studies, which would be a minimum requirement for spatially estimating plant-available water on forest sites. The processing of resistivity data by pedotransfer functions like Archie’s law (Archie 1942), should also be supplied by wide-ranging physical soil data with probing depths extended at least to the investigation depth of the ERT-measurements. Therefore, drilling is unavoidable for this purpose due to the deep probing depth of ERT-measurements. Finally, a link to aboveground parameters, like topography and stand parameters (e.g., leaf area index or crown geometry), would deliver further information for verifying and interpreting the subsurface data. A complete tree mapping or even airborne or terrestrial laser scans would provide a comprehensive basis for this.
Conclusions
Our results reveal that resistivity changes can be a good proxy for seasonal and interannual soil moisture variations in forest sites. 2D- and 3D-ERT are comparatively non-laborious methods for tracking soil moisture changes in the main rooting zone and the underlying subsurface. Contrary to point measurements traditionally used in forest science, it was possible to record multi-dimensional moisture changes over various scales. These showed that even deeper subsurface areas may be important for long-term findings about the water supply of forest sites, and have not been recorded in classical forest monitoring so far. However, to make quantitative statements about soil moisture, exclusive ERT measurements are insufficient, since the calibration with pF, water content and soil physics is necessary. Nevertheless, this study represents a further step from the laboratory to the field in the application of ERT for monitoring soil moisture of forest sites.
This study also illustrates the importance of a multi-dimensional survey approach for imaging seasonal and interannual soil moisture variations in forest sites. ERT presents an important opportunity to monitor long-term effects of changing climate on vertical and horizontal patterns of soil moisture changes and their impact on single trees.
References
Ahmed AM, Sulaiman WN (2001) Evaluation of groundwater and soil pollution in a landfill area using electrical resistivity imaging survey. Environ Manage 28:655–663. https://doi.org/10.1007/s002670010250
Archie GE (1942) The electrical resistivity log as an aid in determining some reservoir characteristics. Trans AIME 146(1):54–62
Besson A, Cousin I, Dorigny A, Dabas M, King D (2008) The temperature correction for the electrical resistivity measurements in undisturbed soil samples: analysis of the existing conversion models and proposal of a new model. Soil Sci 173(10):707–720. https://doi.org/10.1097/SS.0b013e318189397f
Bieker D, Rust S (2010) Electric resistivity tomography shows radial variation of electrolytes in Quercus robur. Can J Forest Res 40(6):1189–1193. https://doi.org/10.1139/x10-076
Brunet P, Clement R, Bouvier C (2010) Monitoring soil water content and deficit using Electrical Resistivity Tomography (ERT) - A case study in the Cevennes area. France J Hydrol 380(1–2):146–153. https://doi.org/10.1016/j.jhydrol.2009.10.032
Carrière SD, Ruffault J, Pimont F, Doussan C, Simioni G, Chalikakis K, Limousin JM, Scotti I, Courdier F, Cakpo CB, Davi H, Martin-StPaul NK (2020) Impact of local soil and subsoil conditions on inter-individual variations in tree responses to drought: insights from Electrical Resistivity Tomography. Sci Total Environ 698:134247. https://doi.org/10.1016/j.scitotenv.2019.134247
De Jong SM, Heijenk RA, Nijland W, van der Meijde M (2020) Monitoring soil moisture dynamics using Electrical Resistivity Tomography under homogeneous field conditions. Sensors 20(18):5313. https://doi.org/10.3390/s20185313
DWD (2021) Vieljährige Mittelwerte. Deutscher Wetterdienst. https://www.dwd.de/DE/leistungen/klimadatendeutschland/vielj_mittelwerte.html [accessed on 28.10.2021]
Etzold S, Waldner P, Thimonier A, Schmitt M, Dobbertin M (2014) Tree growth in Swiss forests between 1995 and 2010 in relation to climate and stand conditions: recent disturbances matter. For Ecol Manag 311:41–55. https://doi.org/10.1016/j.foreco.2013.05.040
Evett SR (2003) Soil water measurement by time domain reflectometry. Encycl Water Sci. https://doi.org/10.1081/E-EWS120010152
Furman A, Ferré TP, Warrick AW (2003) A sensitivity analysis of electrical resistivity tomography array types using analytical element modeling. Vadose Zone J 2(3):416–423. https://doi.org/10.2113/2.3.416
Gerke J (1992) Phosphate, aluminum and iron in the soil solution of three different soils in relation to varying concentrations of citric acid. J Plant Nutr Soil Sc 155(4):339–343. https://doi.org/10.1002/jpln.19921550417
Gracia CA, Tello E, Sabaté S, Bellot J (1999) GOTILWA: an integrated model of water dynamics and forest growth. In: Rodà F, Retana J, Gracia CA, Bellot J (eds) Ecology of mediterranean evergreen oak forests ecological studies. Springer, Berlin
Grayston SJ, Vaughan D, Jones D (1997) Rhizosphere carbon flow in trees, in comparison with annual plants: the importance of root exudation and its impact on microbial activity and nutrient availability. Appl Soil Ecol 5:29–56
Günther T, Rücker C, Spitzer K (2006) Three-dimensional modelling and inversion of DC resistivity data incorporating topography—II. Inversion Geophys J Int 166(2):506–517. https://doi.org/10.1111/j.1365-246X.2006.03011.x
Hadzick ZZ, Guber AK, Pachepsky YA, Hill RL (2011) Pedotransfer functions in soil electrical resistivity estimation. Geoderma 164(3–4):195–202. https://doi.org/10.1016/j.geoderma.2011.06.004
Hayley K, Bentley L, Pidlisecky A (2010) Compensating for temperature variations in time-lapse electrical resistivity difference imaging. J Geophysics 75(4):51–59. https://doi.org/10.1190/1.3478208
Ikard SJ, Revil A, Schmutz M, Karaoulis M, Jardani A, Mooney M (2014) Characterization of focused seepage through an earthfill dam using geoelectrical methods. Ground Water 52(6):952–965. https://doi.org/10.1111/gwat.12151
Ionita M, Tallaksen LM, Kingston DG, Stagge JH, Laaha G, Van Lanen HA, Scholz P, Chelcea SM, Haslinger K (2017) The European 2015 drought from a climatological perspective. Hydrol Earth Sys Sci 21(3):1397–1419. https://doi.org/10.5194/hess-21-1397-2017
Jayawickreme DH, Van Dam RL, Hyndman DW (2008) Subsurface imaging of vegetation, climate, and root-zone moisture interactions. Geophys Res Lett 35(18):L18404. https://doi.org/10.1029/2008GL034690
Kneisel C, Emmert A, Kastl J (2014) Application of 3D electrical resistivity imaging for mapping frozen ground conditions exemplified by three case studies. Geomorphology 210:71–82. https://doi.org/10.1016/j.geomorph.2013.12.022
Kneisel C, Emmert A, Polich P, Zollinger B, Egli M (2015) Soil geomorphology and frozen ground conditions at a subalpine talus slope having permafrost in the eastern Swiss Alps. CATENA 133:107–118. https://doi.org/10.1016/j.catena.2015.05.005
Kneisel C, Hauck C (2008) Electrical methods. In: Hauck C, Kneisel C (eds) Applied geophysics in periglacial environments. Cambridge University Press, Cambridge, pp 3–27
Knödel K, Krummel H, Lange G (2013) Handbuch zur Erkundung des Untergrundes von Deponien und Altlasten: Band 3: Geophysik. Springer, New York
LDBV (2021) Digitales Geländemodell 25m. Landesamt für Digitalisierung, Breitband und Vermessung
Loke MH (2004) Tutorial: 2-D and 3-D electrical imaging surveys. https://sites.ualberta.ca/~unsworth/UA-classes/223/loke_course_notes.pdf [accessed on 28.10.2021]
Ma Y, Van Dam RL, Jayawickreme DH (2014) Soil moisture variability in a temperate deciduous forest: insights from electrical resistivity and throughfall data. Environ Earth Sci 72(5):1367–1381. https://doi.org/10.1007/s12665-014-3362-y
Mellert KH, Ewald J (2014) Nutrient limitation and site-related growth potential of Norway spruce (Picea abies [L.] Karst) in the Bavarian Alps. Eur J Forest Res 133(3):433–451. https://doi.org/10.1007/s10342-013-0775-1
Mellert KH, Lenoir J, Winter S, Kölling C, Carni A, Dorado-Linan I, Gegout JC, Göttlein A, Hornstein D, Jantsch M, Juvan N, Kolb E, Lopez-Senespleda E, Menzel A, Stojanovic D, Tager S, Tsiripidis I, Wohlgemuth T, Ewald J (2018) Soil water storage appears to compensate for climatic aridity at the xeric margin of European tree species distribution. Eur J Forest Res 137(1):79–92. https://doi.org/10.1007/s10342-017-1092-x
Michot D, Benderitter Y, Dorigny A, Nicoullaud B, King D, Tabbagh A (2003) Spatial and temporal monitoring of soil water content with an irrigated corn crop cover using surface electrical resistivity tomography. Water Resour Res 39(5):1138. https://doi.org/10.1029/2002WR001581
Mitscherlich G (1971) Wald, Wachstum und Umwelt: Waldklima und Wasserhaushalt. 2nd Edition. Sauerländer. p 36
Návar J (2011) Stemflow variation in Mexico’s northeastern forest communities: its contribution to soil moisture content and aquifer recharge. J Hydrol 408(1–2):35–42. https://doi.org/10.1016/j.jhydrol.2011.07.006
Netherer S, Panassiti B, Pennerstorfer J, Matthews B (2019) Acute drought is an important driver of bark beetle infestation in Austrian Norway spruce stands. Front Forests Global Change 2:39. https://doi.org/10.3389/ffgc.2019.00039
Nijland W, van der Meijde M, Addink EA, de Jong SM (2010) Detection of soil moisture and vegetation water abstraction in a Mediterranean natural area using electrical resistivity tomography. CATENA 81(3):209–216. https://doi.org/10.1016/j.catena.2010.03.005
Nivorlis A, Dahlin T, Rossi M, Höglund N, Sparrenbom C (2019) Multidisciplinary characterization of chlorinated solvents contamination and in-situ remediation with the use of the direct current resistivity and time-domain induced polarization tomography. Geosciences 9(12):487. https://doi.org/10.3390/geosciences9120487
Norooz R, Olsson P-I, Dahlin T, Günther T, Bernstone C (2021) A geoelectrical pre-study of Älvkarleby test embankment dam: 3D forward modelling and effects of structural constraints on the 3D inversion model of zoned embankment dams. J Appl Geophys 191:104355. https://doi.org/10.1016/j.jappgeo.2021.104355
Oishi AC, Oren R, Novick KA, Palmroth S, Katul GG (2010) Interannual invariability of forest evapotranspiration and its consequence to water flow downstream. Ecosystems 13(3):421–436. https://doi.org/10.1007/s10021-010-9328-3
Reynolds JM (2011) An introduction to applied and environmental geophysics, 2nd edn. Wiley, New Jersey
Rücker C, Günther T, Spitzer K (2006) Three-dimensional modelling and inversion of dc resistivity data incorporating topography—I. Modelling Geophys J Int 166(2):495–505. https://doi.org/10.1111/j.1365-246X.2006.03010.x
Samouelian A, Cousin I, Tabbagh A, Bruand A, Richard G (2005) Electrical resistivity survey in soil science: a review. Soil till Res 83(2):173–193. https://doi.org/10.1016/j.still.2004.10.004
Schmidt-Vogt H (1986) Die fichte. Volume II. 2nd Edition. Parey. p 647
Schuldt B, Buras A, Arend M, Vitasse Y, Beierkuhnlein C, Damm A, Gharun M, Grams TEE, Hauck M, Hajek P, Hartmann H, Hiltbrunner E, Hoch G, Holloway-Phillips M, Körner C, Larysch E, Lübbe T, Nelson DB, Rammig A, Rigling A, Rose L, Ruehr NK, Schumann K, Weiser F, Werner C, Wohlgemuth T, Zang CS, Kahmen A (2020) A first assessment of the impact of the extreme 2018 summer drought on Central European forests. Basic Appl Ecol 45:86–103. https://doi.org/10.1016/j.baae.2020.04.003
Seladji S, Cosenza P, Tabbagh A, Ranger J, Richard G (2010) The effect of compaction on soil electrical resistivity: a laboratory investigation. Eur J Soil Sci 61(6):1043–1055. https://doi.org/10.1111/j.1365-2389.2010.01309.x
Srayeddin I, Doussan C (2009) Estimation of the spatial variability of root water uptake of maize and sorghum at the field scale by electrical resistivity tomography. Plant Soil 319(1):185–207. https://doi.org/10.1007/s11104-008-9860-5
Taniguchi M, Tsujimura M, Tanaka T (1996) Significance of stemflow in groundwater recharge. 1: evaluation of the stemflow contribution to recharge using a mass balance approach. Hydrol Processes 10(1):71–80
Van Reeuwijk LP (1992) Procedures for soil analysis. International Soil Reference and Information Centre, Wageningen
Werban U, Al Hagrey SA, Rabbel W (2008) Monitoring of root-zone water content in the laboratory by 2D geoelectrical tomography. J Plant Nutr Soil Sci 171(6):927–935. https://doi.org/10.1002/jpln.200700145
White PA (1988) Measurement of ground-water parameters using salt-water injection and surface resistivity. Groundwater 26(2):179–186. https://doi.org/10.1111/j.1745-6584.1988.tb00381.x
Acknowledgements
We are grateful for the support of the Bavarian Institute of Forestry (LWF) and the provision of soil moisture data for the forest monitoring plot in Würzburg. Special thanks also go to Adrian Emmert, Julia Rieder, and Tim Wiegand, who helped in installing, maintaining, and measuring the ERT-monitoring.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Project funding: This scientific study could be realized with the help of two start-up funds (the so-called research fund of the University of Würzburg and a university sponsorship award of the Mainfränkische Wirtschaft), both of which were applied for and awarded to C. Kneisel. Based on these preliminary investigations, a longer-term third-party funded project could be realized (2218WK22X1).
The online version is available at http://www.springerlink.com.
Corresponding editor: Yu Lei.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fäth, J., Kunz, J. & Kneisel, C. Monitoring spatiotemporal soil moisture changes in the subsurface of forest sites using electrical resistivity tomography (ERT). J. For. Res. 33, 1649–1662 (2022). https://doi.org/10.1007/s11676-022-01498-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11676-022-01498-x