Introduction

In nature, individual tree species have a specific distribution in a diversity of habitats along pronounced environmental gradients (Johnson et al. 2006; Frenne et al. 2013; López-Goldar and Agrawal 2021). The diversity of environments and selection pressures in distribution have led to population variations. Climatic gradients, such as precipitation and temperature when they play major roles in selection, the variation of a population may be predicted (Vanhove et al. 2021; Aschero et al. 2022). However, precondition is for a large population, often suggesting that the distribution of genetic and phenotypic variations follow similar patterns, reflecting a correlation for a given trait and climatic factors (Ingvarsson and Street 2011; McKown et al. 2014; Mu et al. 2021). During a period of global climate fluctuations, provenance trials of species within relative homogenous environments are necessary to explore phenotypic variations across narrow habitats in diverse geographical ranges. Large data sets collected in plantings can provide good growth and survival data, and good estimates of genetic parameters for breeding purposes so as to find the best provenances for afforestation and propagation materials for breeding (Hodge and Dvorak 2015; Pan et al. 2020).

The logistic equation, a growth model that parameterizes the complete growth process of an organism or a population, reflects the regularity of certain organism growth (Boris 1993) and can be used to calculate maximum biomass and annual growth in provenance trails, eliminating redundant data and subsequent analysis. The growth equation may also be used to monitor the growth of L. kaempferi, allowing researchers to investigate the relationship between geography and climate and growth curve parameters (Magnussen and Park 1991; Rammig et al. 2007; Shater et al. 2011; Nagamitsu et al. 2013; Mu et al. 2021). Growth curve parameters are no longer limited to analyzing the impact of the environment on growth, but consider correlations between climate and future growth which could show the phenotypic plasticity of the provenances.

Larix kaempferi (Lamb.) Carr. (Japanese larch) is one of the most successful introduced tree species for wood production and pulp and paper in Europe, Asia, and North America. The natural habitat of L. kaempferi is restricted to 900–3100 m elevations in a narrow 200 km2 in central Honshu Island (Hayashi 1960; Hoshi 2004). It grows rapidly under ideal conditions and occasionally outgrows indigenous larch species (Paques 1996; Jose-Maldia et al. 2009). For successful large-scale breeding, multi-site provenance trials were designed to discover provenances for breeding in each climatic zone and to clarify the relationship between provenance and environment. (Langlet 1971; Lortie and Hierro 2021). Previous studies of L. kaempferi and other conifers have demonstrated that provenance is related to key geoclimatic variables, implying that certain environmental conditions limit growth and adaptability (Filipiak and Napierala-Filipiak 2008; Leonelli et al. 2009; Maaten-Theunissen and Bouriaud 2012; Nagamitsu et al. 2013). For alpine L. kaempferi, high altitude increases productivity and might be the main habitat of the species in the future (Wu et al. 2021). This might be because L. kaempferi is distributed at high altitudes and has the characteristics of island-like distribution, the barrier of high mountains makes it difficult for gene communication, enabling it to retain the characteristics of alpine plants. In tree breeding, the evaluation of genetic parameters is essential for the selection of plus trees in different regions and for the formulation of breeding strategies. (Park and Fowler 1983; Arcade et al. 1996; Zhang et al. 2022). Moreover, establishing provenance trials and seed orchards is effective for calculating genetic parameters and for making early selections to increase productivity and broadening the genetic base of the current breeding population of L. kaempferi outside its natural distribution area. It is known that successful introduction and domestication needs to consider the environment of the provenance and planting area and needs to repeatedly observe the traits in successive years. Current research on L. kaempferi has rarely investigated the native provenance geoclimate and repeated observation of growth characteristics for years.

Large-scale L. kaempferi seed orchards and progeny testing forests were established in various locations in China in the 1960s. During the 1990s, excellent provenances and families were introduced from Japan for selection and breeding. In recent years, these early progenies L. kaempferi have brought major economic benefits (Pan et al. 2020). The present cultivated area has representative material from the temperate, warm temperate and north subtropical zones of China. It was considered effective to collect L. kaempferi provenances extensively throughout its environmental gradients and combine multi-site provenance trials to explore the relationship between growth and environment to broaden the genetic resource and ensure the best exotic provenances are captured.

In this study, seeds of 84 open-pollinated L. kaempferi families from six provenances along an altitude gradient in the central plateau of Japan were collected in 1996 with the assistance of the Japan International Cooperation Agency (JICA). Two trials were established in northern and southern China of a total of 3,000 seedlings to determine survival rates and growth traits (height, diameter at breast height) and measured each year from 2-years of age to 22-years of age. Growth patterns of the different provenances were evaluated by fitting growth curves of height and diameter at one- to 22- years of age to characterize the performance of the 84 families across two trial sites. Growth parameters and the influence of provenance were estimated and the correlation between provenance and geoclimatic (geography and climate) variables predicted, and the growth curve parameters with significant differences of six provenances determined. Finally, the genetic parameters (variation coefficient, heritability, breeding value) for each growth curve parameter were estimated, as well as the type-B genetic correlation across two sites. Altitude gradients may cause variations in growth parameters and might reflect local adaptability of L. kaempferi by estimating the key geoclimate factors of provenance and comparing growth curve parameter variation between two completely different trials.

Materials and methods

Origin of material and design of tests

Based on a JICA project (Diao et al. 2016), seeds of 84 open-pollinated families were collected from six provenances along an altitude range in the mountains of central Japan, covering the complete native range of L. kaempferi (Table 1; Hoshi 2004). In March 1996, the seeds were germinated and raised to two-year-old seedlings in Jianshi County, Hubei Province, and planted in two trials, HB and LN, located in Hubei Province and Liaoning Province, respectively, two main natural populations of Larix kaempferi. HB is at an altitude of 1700 m, with a cool and humid subtropical monsoon mountain climate; LN is at an altitude of 300 m, with a hot and dry temperate continental monsoon climate (Table 2).

Table 1 Location and natural conditions of six provenances and families of Larix kaempferi
Full size table
Table 2 Location and natural conditions of two trials (HB and LN represent Hubei and Liaoning, respectively)
Full size table

The trials were randomized complete block design with six blocks of two rows of eight trees. A total of 3000 trees in two trial sites. To ensure long-term trial health, low thinning was carried out at ages 10 and 14 in each trial plot. In the last survey, because of thinning and mortality, approximately total of 2000 trees remained in the two trial plots.

Data collection

Height (HGT, m) and diameter at breast (DBH, cm) were both measured at ages 2 − 4, 6 − 9, 11, 12, 16, 17, 22 in HB, and at ages 2, 3, 6, 7, 8, 17, 22 in LN. Based on published studies, twenty-five geoclimate factors relevant to the growth of L. kaempferi were chosen to characterize each provenance (Rehfeldt et al. 2003; Nagaike 2010; Nagamitsu et al. 2013). Table S1-1 shows altitude, latitude, and longitude acquired from portable GPS units, as well as 22 averaged climatic variable estimates from 1961 to 2000 obtained from ClimateAP (Table S1-2; Wang et al. 2017).

Statistical analysis

Growth curve parameters analysis

In most years, substantial variations of height and DBH occurred among provenances and families (Table S2). To explain this in detail, the growth process was parameterized. The following equation was used to fit the growth curve for HGT and DBH to evaluate the growth trend uniformity at the provenance level:

$$P(t)=a/(1+b{e}^{-rt})$$
(1)

where \(t\) is the age, \(P(t)\) the average phenotype value at the provenance level at age t; a is the maximum value of the phenotype; b is the initial growth parameter,\(a/(1+b)\) the initial value of the phenotype (t = 0); r is the relative rate.

The growth parameters a, b, and r were estimated using deSolve package in R 4.0.5 (Soetaert et al. 2010) with the principle of maximum R2 value for better fitting. Three physiologically significant points on the logistic curve, namely points of maximum acceleration (\({t}_{a},{g}_{a}\)), the important point (\({t}_{i},{g}_{i}\)), and points of minimum acceleration (\({t}_{d},{g}_{d}\)), and the fast-growth period (\(\Delta \mathrm{T}\)) were calculated for each provenance as follows:

$$\left({t}_{a},{g}_{a}\right)=\left(\frac{\mathrm{ln}b\left(2-\sqrt{3}\right)}{r},\frac{a\left(3-\sqrt{3}\right)}{6}\right)$$
(2)
$$\left({t}_{i},{g}_{i}\right) =\left(\frac{\mathrm{ln}b}{r},\frac{a}{2}\right)$$
(3)
$$\left({t}_{d},{g}_{d}\right)=\left(\frac{\mathrm{ln}b\left(2+\sqrt{3}\right)}{r},\frac{a\left(3+\sqrt{3}\right)}{6}\right)$$
(4)
$$\Delta \mathrm{T}={t}_{d}-{t}_{a}$$
(5)

where \({t}_{a}\) the time of maximum acceleration, \({g}_{a}\) the phenotype value at \({t}_{a}\), \({t}_{i}\) the time of maximum growth rate, \({g}_{i}\) the phenotype value at \({t}_{i}\), \({t}_{d}\) the time of minimum acceleration, \({g}_{d}\) the phenotype value at \({t}_{d}\), and \(\Delta \mathrm{T}\) the duration of the fast-growing period.

An analysis of variance was carried out of the growth curve parameters (a, b, r, \({t}_{a}\), ga, \({t}_{i}\), \({g}_{i}\), \({t}_{d}\) \({g}_{d}\), \(\Delta \mathrm{T}\)) of 84 families and six provenances on the two trial sites using the statistical software ASReml-R (v. 3.0, Queensland Department of Primary Industries and Fisheries, Brisbane, Australia) in R (Butler et al. 2009). The following linear models were used:

$${y}_{ijkl}={S}_{i}+{P}_{j}+F(P{)}_{kj}+S{P}_{ij}+SF(P{)}_{ijk}+{e}_{ijkl}$$
(6)
$${y*}_{ijkl}={P}_{j}+F(P{)}_{kj}+{B}_{i}+{PB}_{ij}+F(P{)B}_{ijk}+{e}_{ijkl}$$
(7)

where \({y}_{ijkl}\) and \({y*}_{ijkl}\) are the growth curve parameters (a, b, r), the parameter of three physiologically significant points and \(\Delta \mathrm{T}\), \({S}_{i}\) the effect of site i, \({P}_{j}\) the effect of provenance j; \(F(P{)}_{kj}\) is the effect of family k within provenance j; \(S{P}_{ij}\) is the effect of interaction between site i and provenance j; and \(SF(P{)}_{ijK}\) is the effect of the interaction between site i and family k within provenance j, Bi the fixed effect of the \(i\) block, \({e}_{ijkl}\) the random error. The statistical significance of parameters was tested by Wald tests.

Variance and genetic variation estimation

The following mixed linear models were used to estimate genetic parameters:

$${Y}_{ijkl}=\mu +{P}_{i}+F(P{)}_{ij}+{B}_{k}+P{B}_{ik}+F(P){B}_{ijk}+{e}_{ijkl}$$
(8)

where \({Y}_{ijkl}\) is growth curve parameter and individual-tree a, b, r was used as the unit of observation. Since other growth curve parameters were all variants of a, b, r, only the key parameters were analyzed; \(\mu\) is the mean value of the growth parameters; \({P}_{i}\) is the random effect of provenances, which follows the NID (0,\({\hat{\sigma }}_{p}^{2}\)), \(i\)=1,2,3,4,5,6; \(F(P{)}_{ij}\) is the random effect of family \(j\) within provenances, which follows the NID (0,\({\hat{\sigma }}_{f}^{2}\)) i,\(j\)= 1,2,…,20 for Kusatsu, j = 1,2,…,6 for Asama, \(j\)= 1,2,…,16 for Fuji, \(j\)= 1,2,…,15 for Ina, \(j\)= 1,2,…,18 for Nikko, \(j\)= 1,2,…,9 for Matsumoto; \({B}_{k}\) is the fixed effect of the \(k\) block,\(k\)= 1,2,3,4,5,6;\(P{B}_{ik}\) is the random interaction effect of the provenance i by the k block which follows the NID (0,\({\hat{\sigma }}_{pb}^{2}\)); \(F\left(P\right){B}_{ijk}\) is the random interaction effect of the family \(j\) in i provenance by the k block which follows the NID (0,\({\hat{\sigma }}_{fb}^{2}\)); \({e}_{ijkl}\) is the random error which follows the NID (0,\({\hat{\sigma }}_{e}^{2}\)).

Variance components of random effects were estimated by the average information restricted maximum likelihood (REML) algorithm in the statistical software ASReml-R (v. 3.0, Queensland Department of Primary Industries and Fisheries, Brisbane, Australia) package in R (Butler et al. 2009). Approximate standard errors of estimated parameters were estimated using a standard Taylor series expansion method with ASReml-R (Gilmour et al. 2009). The statistical significance of the variance components for each trait was determined using a two-tailed likelihood ratio test (LRT) (Self and Liang 1987), where the test is against the null hypothesis of the estimated parameter equaling zero. Provenance effects and forest stand effects within-provenance were predicted using Best Linear Unbiased Prediction (BLUP) for the two sites.

The amount of provenance variance was calculated as:

$${\widehat{P}}^{2}= \frac{{\hat{\sigma }}_{p}^{2}}{\hat{\sigma }_{phen}^{2}}$$
(9)
$${\hat{\sigma }}_{phen}^{2}={\hat{\sigma }}_{p}^{2}+{\hat{\sigma }}_{f}^{2}+{\hat{\sigma }}_{pb}^{2}+{\hat{\sigma }}_{fb}^{2}+{\hat{\sigma }}_{e}^{2}$$
(10)

The individual tree heritability (\({\hat{h}}_{i}^{2}\)) was calculated as:

$${\widehat{h}}_{i}^{2}=\frac{4\times {\hat{\sigma }}_{f}^{2}}{({\hat{\sigma }}_{f}^{2}+{\hat{\sigma }}_{fb}^{2}+{\hat{\sigma }}_{e}^{2})}$$
(11)

The phenotypic coefficient of variance (\({\widehat{CV}}_{P}\)), the provenance variation coefficient (\({\widehat{CV}}_{prov}\)) and genetic variation coefficient (\({\widehat{CV}}_{G}\)) were calculated using the following equations:

$${\widehat{CV}}_{P}=\frac{\sqrt{{\hat{\sigma }}_{phen}^{2}}}{\overline{X}}\times 100$$
(12)
$${\widehat{CV}}_{prov}=\frac{\sqrt{{\hat{\sigma }}_{p}^{2}}}{\overline{X}}\times 100$$
(13)
$${\widehat{CV}}_{G}=\frac{\sqrt{{\hat{\sigma }}_{f}^{2}}}{\overline{X}}\times 100$$
(14)

where \(\overline{X}\) is the over mean of growth curve parameter.

Genotype by environment correlation analysis

The following linear model was used to analyze the grow curve parameters of the provenances and families within six provenances by site interaction:

$${Y}_{ijklm}=\mu +{S}_{i}+B(S{)}_{ik}+{P}_{l}+{PS}_{il}+{F(P)}_{jl}+F(P){S}_{ijl}+{w}_{ijklm}$$
(15)

where \({Y}_{ijklm}\) is the value of growth curve parameter;\(\mu\) is the mean value of the growth curve parameters; \({S}_{i}\) is the fixed effect of sites; \(B(S{)}_{ik}\) is the fixed effect of block \(k\) in \(i\) site, \(P\) the random effect of the \(l\) provenance which follows the NID (0,\({\hat{\sigma }}_{p}^{2}\)), \({PS}_{il}\) the random interaction effect between the provenance l and the \(i\) site which follows the NID (0,\({\hat{\sigma }}_{sp}^{2}\)), \({F(P)}_{jl}\) is the random effect of family \(j\) in provenance \(l\) which follows the NID (0,\({\hat{\sigma }}_{f}^{2}\)); \(F(P){S}_{ijl}\) is the random interaction effect between family \(j\) in provenance \(l\) and site \(i\), which follows the NID (0,\({\hat{\sigma }}_{sf}^{2}\)); \({w}_{ijklm}\) is the random error which follows the NID (0,\({\hat{\sigma }}_{e}^{2}\)).

To interpret genotype \(\times\) environment, the type-B genetic correlations of growth curve parameters (a, b, r) of six provenances and 84 families on two sites were estimated (Burdon 1977), the type-B provenance and family correlations (\(r{B}_{prov}\) and \(r{B}_{f}\)) were estimated as:

$$r{B}_{prov}=\frac{{\hat{\sigma }}_{p}^{2}}{{\hat{\sigma }}_{p}^{2}+{\hat{\sigma }}_{sp}^{2}}$$
(16)
$$r{B}_{f}=\frac{{\hat{\sigma }}_{f}^{2}}{{\hat{\sigma }}_{f}^{2}+{\hat{\sigma }}_{sf}^{2}}$$
(17)

Values of \(rB\) are close to 1.0 indicates no interaction, while values near 0.0 indicates highly significant interaction (Burdon 1977).

Geoclimatic correlation analysis

For the correlation with geoclimate, growth curve parameters that differed significantly between provenances were considered. The significant different (P < 0.1) growth variables of two sites were selected and combined into one matrix and the growth-geoclimatic correlation between them was analyzed with the geoclimatic variables of the original provenance locations. Pearson’s correlation analysis and Mantel-test statistics were used to estimate multiple climate factor correlations and correlation strength. All correlation analysis and drawings used R 4.0.5 (Ginestet 2011).

Results

The variation of growth curve parameters (a, b, r, \({t}_{a}\), \({g}_{a}\), \({t}_{i}\), \({g}_{i}\), \({t}_{d}\), \({g}_{d}\), \(\Delta \mathrm{T}\)) at a single trial site were studied and the influence of provenance compared. The relationships between provenance-related growth parameters and provenance geoclimatic factors were also investigated. Across two trials with different climates, genetic parameters of growth were estimated, including phenotypic and genetic variations and the genotype-environment interaction.

Variations of growth and growth curve parameters

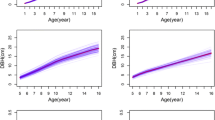
Height and DBH among provenances and families measured in HB and LN revealed significant differences (Table S2). The estimated growth curves of height and DBH were used to characterize the growth of the six provenances from one- to 22- years of age for the two trial sites (Fig. 2), and the growth curves for families of each provenance assessed the differences more intuitively between the same provenance (Fig. S1). LN had more substantial differences in growth traits and growth curve parameters (\({t}_{a}\), \({g}_{a}\), \({t}_{i}\), \({g}_{i}\), \({t}_{d}\), \({g}_{d}\), \(\Delta \mathrm{T}\)) than HB, and the differences in DBH were more noticeable than those for height (Tables S2, S3). The HGT growth curve parameter a (HGTa) showed significant differences among the six provenances and 84 families in HB (P < 0.01). For DBHa and DBHr, there were significant difference among provenances (P < 0.01) in LN. The growth of L. kaempferi was affected by the planting environment. Substantial differences of growth curve parameters (a, b, r, \({t}_{a}\), \({g}_{a}\), \({t}_{i}\), \({g}_{i}\), \({t}_{d}\), \({g}_{d}\), \(\Delta \mathrm{T}\)) were also found between the same provenance at the two sites (Table S3, Fig. 1).

Fig. 1
figure 1

Map of provenance and climate variables of six Larix kaempferi provenances along an altitude gradient of central Japan for 1961 − 1990

Full size image
Fig. 2
figure 2

Growth curve of different provenances in the two sites; HGT of Larix kaempferi in HB (H-HGT), the DBH at HB (H-DBH), the HGT at LN (L-HGT), the DBH at LN (L-DBH). Six color lines indicate the provenances: ‘Kusatsu’, ‘Asama’, ‘Fuji’, ‘Ina’, ‘Nikko’, ‘Matsumoto’; the points on the curves indicate the important points (\({t}_{i}\), \({g}_{i}\)) of different provenances, the triangles the points of maximum acceleration (\({t}_{a}\), \({g}_{a}\)), the squares the points of minimum acceleration (\({t}_{d}\), \({g}_{d}\)); R2 is the average of the coefficient of determination, R2' is R2 after adjusting

Full size image

The Ina provenance outperformed other provenances in terms of height and DBH at both sites. The Matsumoto provenance was superior over other provenances in LN with a temperate continental climate. The fast-growing period duration (\(\Delta \mathrm{T}\)) of all provenances for height and DBH in HB ranged from 6- to 8- years of age, and in LN, it was 5- to 7-years of age. The six provenances at HB had larger diameter growth than corresponding provenances in LN, but exhibited distinctly lower height, and the \({t}_{i}\) (the time of maximum growth rate) of DBH occurred later.

Genetic parameters

The variation coefficients \({\widehat{CV}}_{P}\), \({\widehat{CV}}_{prov}\), and \({\widehat{CV}}_{G}\) of the growth curve parameters (a, b, r) at both sites are shown in Table 3. The estimates of \({\widehat{CV}}_{P}\), \({\widehat{CV}}_{prov}\), and \({\widehat{CV}}_{G}\) for HGT growth curve parameters in HB were higher than those in LN. On the other hand, \({\widehat{CV}}_{G}\) and \({\widehat{CV}}_{prov}\) for DBH growth curve parameters in HB were lower than those in LN (Table S4). HGTr had the highest estimates of \({\widehat{CV}}_{prov}\) (3.0%), and \({\widehat{CV}}_{G}\) (7.9%) among the growth curve parameters in HB. At both sites, the \({\widehat{CV}}_{P}\) of DBHa was the highest (69.7% in HB and 47.1% in LN), and the \({\widehat{CV}}_{P}\) of HGTr (1.7% in HB and 0.8% in LN) and DBHr (0.5% in HB and 0.6% in LN) were the lowest. In general, the estimated phenotypic variation coefficients were higher than the family genetic variation coefficient levels.

Table 3 Variance components with standard error (SE) in parentheses (\({\widehat{P}}^{2}, {\hat{\sigma }}_{f}^{2}, {\hat{\sigma }}_{pb}^{2},{\hat{\sigma }}_{fb}^{2}\) represent the variance components ofprovenance, family, provenance by block and family by block respectively) and genetic parameters (\({\hat{h}}_{i}^{2}, {\widehat{CV}}_{prov}, {\widehat{CV}}_{G}, {\widehat{CV}}_{p}\) represent the individual heritability, provenance variation coefficient, genetic variation coefficient and phenotypic variation coefficient) for growth curve parameter (HGTa, HGTb, HGTr, DBHa, DBHb, DBHr; HGT and DBH followed by growth curve parameter represent this parameter of HGT or DBH) in two sites (HB and LN represent Hubei and Liaoning respectively)
Full size table

The provenance variance components and individual tree heritability (\({\hat{h}}_{i}^{2}\)) estimates for growth curve parameters were showed in Table 3. Significant provenance variation was evident for HGTa in HB, with \({\widehat{P}}^{2}\) = 0.04, \({\hat{h}}_{i}^{2}\) = 0.11, and DBHa and DBHr in LN, with \({\widehat{P}}^{2}\) = 0.07, \({\hat{h}}_{i}^{2}\) = 0.23 for DBHa, 0.37 for DBHr. Under two different environmental conditions, the heritability estimates of the same growth curve parameters behaved differently and showed a quite similar pattern to \({\widehat{CV}}_{G}\). The \({\hat{h}}_{i}^{2}\) for DBHa (0.23 vs. 0.05) and DBHr (0.37 vs. 0.34) in LN were higher than those in HB. In HB, the estimated heritability was the highest for HGTr (\({\hat{h}}_{i}^{2}\) = 0.54). In LN, the estimated heritability was the highest for DBHb (\({\hat{h}}_{i}^{2}\) = 0.46).

The BLUPP value (random provenance effects) obtained from the mixed models are used to evaluate the future provenance’s performance. The ranking BLUPP values of growth curve parameters for HGT and DBH at both sites were showed in Table S5. Matsumoto may be the most adaptive provenance at both sites in the future, and the BLUPp value of growth curve parameters of Ina and Fuji provenance ranks higher than other provenances. It was also worth noting that HGTa had the highest provenance effect (0.42) in HB and DBHa had the greatest provenance effect (0.67) in LN. The provenance effects of growth curve parameters in HB with positive values were higher than those in LN.

Growth-geoclimate correlation

Most climate variables were significantly correlated. The PAS, NFFD, Eref, and MAT were strongly correlated to each other, and PAS, NFFD and Tmin_JJA were strongly related to each other (Fig. S2). The majority of geoclimate variables were strongly related to altitude, including MAT (r =  − 0.94, P < 0.001), MCMT (r =  − 0.97, P < 0.001), AHM (r =  − 0.9, P < 0.001), NFFD (r =  − 0.95, P < 0.001), PAS (r = 0.9, P < 0.001), Tmax_DJF (SON) (r =  − 0.97 (− 0.96); P < 0.001), Tmin_DJF (JJA, SON) (r > 0.9, P < 0.001). The correlation between geoclimate variables and three growth curve parameters (HGTa, DBHa, and DBHr) with significant differences varied greatly, but they were all related to altitude (r = 0.52, 0.57, -0.45; P < 0.001), PAS and Tmax_JJA (P < 0.01) (Fig. 3). The growth matrix had no relationship with latitude, which could be attributed to the non-significant variation in latitude between provenances. There was a significant difference in the correlations between longitude and DBHa and DBHr (0.01 < Mantel’s P < 0.05, Mantel’s r < 0.25). HGTa and DBHa showed significant negative correlation with temperature variables (P < 0.01), and the DBHr showed significant positive correlations with Tmax_JJA (r = 0.39, P < 0.01) and negative related with MAP (r =  − 0.62, P < 0.01) and PPT_MAM (r =  − 0.41, P < 0.01). The DBHa and DBHr were more strongly regulated by climate variables than HGT, suggesting that the growth in DBH may be more pronouncedly affected by climate.

Fig. 3
figure 3

Phenotypic traits and growth parameters matrix correlations. The geoclimate variables (MAT, MAP, AHM, NFFD, PAS, Eref, Tmax/min_DJF, Tmax/min_MAM, Tmax/min_JJA, Tmax/min_SON, PPT_DJF, PPT_MAM, PPT_JJA, PPT_SON) are listed in Table S1. The lower part: Pearson correlation coefficient (Pearson’s r) is indicated among these geoclimate variables and 1 is indicated by light blue and − 1 by brown; ‘***’ indicates P < 0.001, ‘**’ P < 0.05, ‘*’ P < 0.1. The upper part: Mantel correlation coefficient (Mantel’s r) between significantly different grow curve parameters (Table 3) and geoclimate variables are shown, thick line indicates a Mantel correlation coefficient of 0.25 − 0.5 and the thin line indicates that the Mantel correlation coefficient is lower than 0.25, the red line indicates 0.001 > P > 0.01, the blue line 0.01 > P > 0.05, the grey line P  ≥ 0.05

Full size image

Genotype by environment interaction

The results of type-B genetic correlations (\(rB\)) showed that environmental adaption of the same provenance differed across the two sites. The estimation of \(rB\) was conducive to the regionalization of trees. Table 4 shows the estimated \(rB\) values of family (\(r{B}_{f}\)) and provenance (\(r{B}_{prov}\)) for grow curve parameters (HGTa/b/r, DBHa/b/r). The HGTr and DBH growth curve parameters were significantly influenced by provenance and environment interaction; the growth curve parameters of DBH were significantly influenced by family and environment interaction (\(rB\)< 0.67), suggesting that DBH was more vulnerable to environmental fluctuations.

Table 4 Type-B genetic correlation (represents the provenance and family type-B genetic correlation) with standard error (SE) in parentheses across two sites
Full size table

Discussion

Provenance altitude and species adaptability

The dynamic shift in the growth curve parameter was correlated with geoclimatic variables that were static in spatiotemporal stability and reflected distinct selection factors. Because the habitats of L. kaempferi were distributed along altitude gradients and the different provenances were separated by mountains, gene flow had little impact on provenance adaptive differentiation. Thus, it could be concluded that, to adapt to different environments, the provenance formed different genetic backgrounds, giving them unique growth and adaptation mechanisms (Stettler and Bradshaw 1994; Vanhove et al. 2021). It is well known that provenances with various genetic backgrounds have phenotypic differences and adaptabilities to new environments (Lopez-Goldar and Agrawal 2021). However, when provenances were transplanted to the same environment, several traits showed no evident variations, possibly because the local climate had ‘erased’ these genotypic distinctions. The new environment may have produced epigenetic variation to activate or silence the gene (Gugger et al. 2016), or it simply created new mutations in the gene. In any case, the success of breeding is determined by whether the beneficial new mutations continue to occur in the offspring (Duncan et al. 2014; Alexander et al. 2015). The annual changes of temperature and precipitation in a geographic area, as well as the growth process of plants, may be affected by altitude differences.

In this study, the growth curve parameters that differed notably between provenances were all significantly related to the provenance's altitude (Fig. 3), and interestingly, climate variables, which were highly correlated with altitude, were also highly correlated with growth curve parameters. The maximum growth values of HGT (height) and DBH were more related to temperature, while the growth rate of DBH appeared to be more affected by precipitation. The results show that altitude change across the range of L. kaempferi, with temperature co-variable by altitude, played a critical role in shaping height maximum phenotypes (HGTa), diameter maximum phenotypes (DBHa), and genetic variation. Precipitation, which showed a weaker association with altitude than temperature, was a major limiting factor in diameter growth rate. This suggests that altitude was a key factor affecting variation and distribution of L. kaempferi.

Low-altitude provenances of other species have long been thought to grow faster than high-altitude ones (Ngulube and Mzomar 1989; Hardawati et al. 2009). However, the altitudes of the provenances were rarely considered to explain this phenomenon. In this study, the same pattern was also observed in L. kaempferi. Moreover, the altitudes of the original provenances have a significant impact on the future adaptability at various altitudes, well beyond our predictions. The Matsumoto provenance showed the greatest effect in the trials with two altitudes, and it adapted well at Liaoning where the altitude was lower, maybe because it originated in high altitudes. In Hubei and Liaoning, the Ina provenance outperformed other provenances. The Asama provenance, which originated in a low altitude area of Japan, performed poorly in Hubei compared to Liaoning. Most of the provenances in this study showed this trend (Fig. 2). It is therefore suggested that expanding variation for traits of interest may be achieved by planting trees from high altitudes to low altitudes where development is more conducive. In addition, altitude gradients induce local adaptation through divergent selection pressures across heterogeneous environments, implying that altitude gradients may be the driving force for local adaptation.

Genetic parameters relationship with breeding

After removing the influence of the different genetic backgrounds, a significant amount of variation was discovered between the same provenances. The parameters with significant differences among the provenances in Hubei were HGTa, and DBHa and DBHr, while in Liaoning, DBHr had a higher heritability of 0.37. Height growth parameters had greater \({\widehat{CV}}_{G}\) and \({\widehat{CV}}_{P}\) in Hubei, while Liaoning provenances had higher \({\widehat{CV}}_{P}\), \({\widehat{CV}}_{prov}\), and \({\widehat{CV}}_{G}\) of DBH growth curve parameters (Table 3). Therefore, height might be a better predictor in early selection in Hubei, while DBH, especially the r value, is more effective in Liaoning. The correlation between the growth curve parameters with geoclimate variables (Fig. 3) and genotype by environmental interaction (Table 4) suggested that DBH was more easily regulated by climatic factors and more susceptible to environmental competition than height. This is consistent with a study of Fagus sylvatica L. (Catherine and Clement 2006). The estimates of variation coefficient for r were always the lowest, indicating that the growth rate of L. kaempferi was strongly influenced by environment. The individual tree heritability of HGTa and HGTr were under stronger genetic control in Hubei with its suitable environment for L. kaempferi growth, and DBHa was under stronger genetic control in Liaoning with an environment quite different from the native environment of L. kaempferi. The strong correlation between provenance effects and altitude at both sites suggests that, when carrying out domestication and breeding programs, it would be wise to pay attention to altitude, and develop breeding efforts for each breeding zone. The genetic parameters (\({\hat{h}}_{i}^{2}\), \({\widehat{CV}}_{G}\)) of single-age growth traits were also estimated (Table S2). It was discovered that individual tree heritability and genetic gain of DBH decreased with increasing age, suggesting that the provenance superiority for diameter in L. kaempferi might gradually weakens over time as it adapts to the environment (Diao et al. 2016).

The \({\widehat{CV}}_{G}\) of DBHa between the two trials exhibited opposite trends in this investigation. It is speculated that, in L. kaempferi, epigenetic variation played a more important role in growth than genetic effects (Duncan et al. 2014; Ci et al. 2016; Gugger et al. 2016; Cai et al. 2021). Future research will need to combine annual climate variables from the planting regions, as well as epigenetic and genetic variants, to explain phenotype and genetic variation at the genome level.

Conclusions

The results revealed that 84 families from six provenances had diverse growth patterns and environmental adaptabilities. Based on the provenance effects predicted from two trials, the Ina provenance was always the most superior, although the Matsumoto provenance is recommended for planting at relatively low altitude environments. By analyzing the geoclimate of the original provenance, it was determined that the climate variables affect growth characteristics, and altitude and precipitation had the strong connection to the adaptation and growth of L. kaempferi.