Introduction

Measurement of individual tree attributes is important for estimating growth and yield as it provides guidelines for decision- making for sustainable forest management (Dau et al. 2015). However, the measurement of all individual tree variables is costly and time-consuming. Diameter at breast height (DBH) and the total height of individual trees are commonly measured variables (Sumida et al. 2013). Compared to DBH, the total height is less frequently measured. Generally, height of sample trees is measured and the height of the rest of the stand is predicted using height-diameter allometry (Peng et al. 2001; Zhang et al. 2014; Bhandari et al. 2021a, 2021b, 2021c). Although DBH can be measured easily, measurement of the upper stem diameter at a particular height is difficult. Taper equations allow for the prediction of upper stem diameters using easily measured variables such as DBH and total height (Kozak and Smith 1966; Kozak et al. 1969; Kozak 2004; Poudel et al. 2018). A taper equation can directly, or through integration, estimate (1) diameter at any point along the stem, (2) the height at a given diameter, (3) total stem volume, (4) merchantable volume and merchantable height to any top diameter from any stump height, and (5) volumes for logs of any length at any height from the ground (Kozak 2004; Poudel et al. 2018).Taper in a tree stem is the rate of decrease in stem diameter from base upwards (Chaturvedi and Khanna 2011) and therefore depends on DBH, total height (H) and upper stem height (h). Taper functions vary in their mathematical form; however, a simple taper function can be represented by Eq. 1.

$$di=f\left(DBH, H, hi\right)$$
(1)

where di is the stem diameter at height hi above the ground for a tree with a diameter at breast height (DBH) and total tree height (H).

The study of tree taper has a long history. Kozak and Smith (1966) and Kozak et al. (1969) recommended a simple quadratic model for describing tree taper. Bruce et al. (1968) developed a polynomial model for predicting upper stem diameter of red alder (Alnus rubra Bong.). Bennett and Swindel (1972) also used a polynomial equation for the upper stem diameter prediction of slash pine (Pinus elliottii Engelm.). All these taper functions assumed that an entire stem has a single form that can be described with a single function. Consequently, these were referred to as single taper functions (Tang et al. 2017). However, the form of a tree stem varies even within a single tree. The basal portion of the stem resembles the frustum of a neiloid, the middle portion with a paraboloid, and the top portion with a conoid (Husch et al. 1972). Realizing the requirement for three different models for three different portions of the stem of an individual tree, Max and Burkhart (1976) developed segmented taper functions for natural and planted loblolly pines (Pinus taeda L.). The segmented taper functions are more accurate than the single taper function because they consider the variation in tree form at different heights.

Tree form varies among species, individual trees of the same species, and within and between stands as well. To account for such variations, Newnham (1988) and Kozak (1988) introduced a variable-exponent taper function which uses changing exponents to compensate for the changes in the form at different sections of the stem (Perez et al. 1990). Several studies have shown that variable exponent taper functions predict upper stem diameters more accurately than the other two types of taper functions (Sharma and Zhang 2004; Rojo et al. 2005; Duan et al. 2016). However, other studies have also reported that better performance of segmented taper functions over variable exponent taper functions (Crecente-Campo et al. 2009; Özçelik and Crecente-Campo 2016; Shahzad et al. 2021). Several studies have been carried out on tree tapers in different areas of the world (Candy 1989; Fang and Bailey 1999; Kozak 2004; Sharma and Patron 2009; Arias-Rodil et al. 2015; Poudel et al. 2018; Silwal et al. 2018; Alkan and Özçelik 2020; Shahzad et al.2021). Most of studies have taken place in North America (Max and Burkhart 1976; Shaw et al. 2003; Sharma and Patron 2009; Li and Weiskittel 2010; Poudel et al.2018), in Europe (Arias-Rodil et al. 2015; Socha et al. 2020), Asia (Fang and Bailey 1999; Tang et al. 2016; Lumbres et al. 2017; Silwal et al. 2018; Shahzad et al. 2021; Koirala et al. 2021) and relatively a lower number in Australia (Gordon 1983; Bi and Turner 1994; Bi 2000), South America (Nunes and Görgens 2016; Beltran et al. 2017) and Africa (Mabvurira and Eerikäinen 2002; Gomat et al. 2011). To our knowledge, only two taper functions have been developed in Nepal and these were developed for S. robusta C.F. Gaertn. (Silwal et al. 2018) and Tectona grandis L. f. (Koirala et al. 2021).

Tree taper depends on species, site, age, and stand density (Sharma and Zhang 2004; Chaturvedi and Khanna 2011; Duan et al. 2016). These variations require different taper equations and are more important in forests with high degree of species diversity, various management regimes, stand density, and human influence. The tropical forests in the western low land of Nepal are rich in diverse species and are managed under different regimes (community forest, leasehold forest, collaborative forest, religious forest, national forest). S. robusta (family Dipterocarpaceae) is one of the dominant and more important timber species in the tropical forests of Nepal. Its distribution ranges from 120 m in the southern lowlands to 1200 m in the middle hills (Jackson 1994; Sah 2000). S. robusta contributes 19.28% (31.76 m3ha–1) in total standing volume and 15.27% in forest type coverage in Nepal (DFRS 2015). S. robusta is a multipurpose species as its stem is used as timber, construction material, and fuelwood (Jackson 1994), leaves as fodder (Kibria et al. 1994) and plates (Kora 2019), and resin as medicine for dysentery and gonorrhea (Joshi 2003). S. robusta forests have the highest total standing volume in Nepal. However, studies in Nepal on the species are limited and mostly focused on volume models (Sharma and Pukkala 1990; Subedi 2017), biomass (Chapagain et al. 2014; Bhandari and Chhetri 2020), form factors (Baral et al. 2020; Chapagain and Sharma 2021; Subedi et al. 2021), regeneration dynamics and diversity (Awasthi et al. 2015, 2020). There is only one study by Silwal et al. (2018) on predicting upper stem diameters of S. robusta. However, their function tested only one form of taper equation, did not consider the effect of stand density, and was based only on 33 individual trees.

The aim of this study was to develop models to predict upper stem diameter and volume of a dominant tree species (S. robusta). Our research questions were: (1) what is the best function to describe tapering in individual trees of S. robusta? (2) does stem taper vary with stand density? (3) is the volume predicted using the taper function more accurate than that predicted by the local volume model? and, (4) is the volume predicted using the taper function more accurate than that predicted by volume models currently used in Nepal?

Materials and methods

Study area

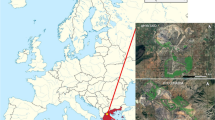
This study used data from a forest of Jogikuti, Shankar Nagar (27°42’ N, 83°28’ E), one of the research sites maintained by the Forest Research and Training Centre, (previously known as Department of Forest Research and Survey) of the Government of Nepal, 25 km northeast of Bhairahawa Airport, Nepal (Fig. 1). The forest was naturally regenerated in 1986 and is dominated by S. robusta or sal. Field measurements were carried out in 2019 when the forest was 33 years old. After a decade of regeneration, stand density was an average of 5200 trees ha–1 (Hartz 1997). The soil is loamy and deep with adequate nutrients. The area has a tropical climate with a long-term average annual rainfall of 1649 mm, 85% from June to September (CBS 2019). Long-term rainfall data shows a declining trend. Mean monthly maximum temperature is 31.1 °C and the mean monthly minimum temperature is 19.2 °C (CBS 2019). The study site is mostly flat with zero to 5% slope.

Fig. 1
figure 1

Map of Nepal showing the study site

Full size image

Experimental design

The research plot covers an area of 92 ha of natural sal forest and is intended to generate information on the growth potential and biomass production of S. robusta under different thinning regimes. The experiment was designed in a randomized complete block design (RCBD) with four treatments and three replications. One of the four treatments was a control; data from the control was not included because the trees were not harvested and taper measurements were unavailable. The remaining three treatments were “natural forest with the highest number of stems ha−1 (500 trees ha–1, T1)”, “natural forest with average number of stems ha−1 (400 trees ha–1, T2)” and “natural forest with the lowest number of stems ha–1 (300 trees ha–1, T3)” (Table 1). The RCBD design minimized any existing unidirectional variability in the study area. Each plot was 100 m × 100 m (1 ha), whereas each block covered an area of 4.7 ha. Spacing between the treatments was a minimum of 5 m buffer on each side. The buffer was also used as a fire line and to make the plot more accessible for silvicultural operations. Spacing between the blocks was at least 50 m.

Table 1 Variables used in this study; diameter at breast height (DBH), upper stem diameter (d), height, and volume; number of trees ha–1 is a stand level variable at 17, 22 and 33 years
Full size table

Sampling and measurement

Fifty-four trees (18 from each treatment) were selected for destructive sampling. The individual trees from each treatment were selected, based on two main criteria. The first was the individual tree must be dominant or co-dominant, the second was the selected dominant or co-dominant trees must be free from disease, decay, and defects on a physical inspection. Once selected, DBH was measured and the tree felled at stump height (at 30 cm from the ground). Total height was measured with a linear tape, and diameter at 1, 2.5, 5, 7.5, 10, 15, 20, 30, 40, 50, 60, 70, 80, and 90% of the total height.

Descriptive statistics of the data

The descriptive statistics of individual trees of all three treatments used in developing taper functions are presented in Table 1. Average DBH was 21.2 cm and minimum and maximum DBH were12.0 and 34.4 cm. Average height was 21.1 m, and minimum and maximum heights were 12.3 and 28.5 m. Average volume of the sample trees was 0.4 m3, and minimum and maximum volumes were 0.1 and 1.0 m3. The distribution of DBH and height showed that the stand was relatively young and had not reached its peak. The scatter plot (not included) of relative diameter and height showed a decreasing trend of diameter with an increase in height.

Model fitting and evaluation

Seventeen commonly used taper functions were fitted to our data and evaluated for their performance (Table 2). To account for the repeated measurement of diameter at different heights of the same tree, a non-linear mixed effect modelling approach was used. In this approach, DBH, total height (H), and height at which upper stem diameter was measured (h) were considered the fixed effect parameters and the individual-tree variation was considered as random effects. Values of all the parameter and fit statistics were estimated using nlme package (Pinheiro et al. 2018) in Rversion4.0.5 (R Core Team 2021). Wherever available, the published values of parameters were used as the initial values in model fitting to facilitate the fast convergence. Orthogonal polynomials were used for predictor variables to minimize the multicollinearity (Bhandari et al. 2021a, 2021c).The fitted taper functions were evaluated using different criteria, including the significance of estimated parameters (at 5% level of significance); coefficient of determination (R2; higher values indicate better models) (Eq. 2); root mean squared error (RMSE; lower values indicate better models) (Eq. 3) (Montgomery et al. 2001); and Akaike information criterion (AIC; lower values indicate better models) (Eq. 4) (Akaike 1972; Burnham and Anderson 2002). The distribution of residuals was plotted against the predicted upper stem diameter to evaluate whether the taper function had a systematic bias. Residuals were also plotted against the predictor variables and examined for evidence of bias. The best three taper functions were selected using the above evaluation criteria.

$${R}^{2}=1- \frac{\sum_{i=1}^{n}{\left({Y}_{i}- {\widehat{Y}}_{i}\right)}^{2}}{\sum_{i=1}^{n}{\left({Y}_{i}- {\overline{Y}}_{i}\right)}^{2}}$$
(2)
$$RMSE= \sqrt{\frac{\sum_{i=1}^{n}{\left({Y}_{i}-{\widehat{Y}}_{i}\right)}^{2}}{n}}$$
(3)
$$AIC= -2\mathrm{ln}\left(L\right)+2p$$
(4)
$$Bias= \frac{\sum_{i=1}^{n}({Y}_{i}-{\widehat{Y}}_{i})}{n}$$
(5)
$$MAE= \frac{\sum_{i=1}^{n}\left|{(Y}_{i}-{\widehat{Y}}_{i})\right|}{n}$$
(6)

where, \({Y}_{i}\) and \({\widehat{Y}}_{i}\) are the observed and predicted values of upper stem diameter, \({\overline{Y}}_{i}\) the average value of the observed upper stem diameter, n the number of observations, \(\mathrm{ln}\) is the natural logarithm, L is likelihood of the fitted taper function and p is the total number of parameters in the taper function; MAE is the mean absolute error.

Table 2 Different taper models used in the study
Full size table

Effect of stand density on taper

The method described by Bhandari et al. (2021b) was used to test the effect of stand density on stem tapering. A linear model of upper stem diameter was fitted as a function of height at which the upper stem diameter was measured (h), total height and DBH was allowed to vary with stand density by including an interaction: d ~ (h- + -H- + -DBH)*Tr, where Tr was the number of stems per ha (stand density). It was then tested whether the effect of stand density (Tr) was significant in the model.

Validation of taper models

The leave-one-out cross-validation (LOOCV) method was used to validate the selected taper function. In this method, one observation was left out for validation and n–1 observations were used for model fitting, where n is the total number of observations used in data collection. This process was continued n times until all the observations were used as validation data. The predicted diameter on validation data was plotted against the observed diameter and the fit statistics including R2, RMSE, and mean absolute error (MAE) were estimated.

Volume prediction

Actual volume calculation

Diameter at different proportions of total height and length between two consecutive diameter measurement points were recorded for each tree (See “Sampling and measurement” section). From the diameter and length of each section, a separate volume was calculated. Formulae of a cylinder (Eq. 7) and cone (Eq. 9) were used to calculate the volume of the stump (30 cm height above the ground) and the top section of individual trees, respectively. Volumes of all other sections were calculated using Smalian’s formula (Eq. 8), as this is commonly used to estimate the volume of small sections accurately (Avery and Burkhart 1994; Chaturvedi and Khanna 2011; Beltran et al. 2017).

$$ {\text{Cylindrical}}\;{\text{volume}} = \frac{{\pi D_{1} ^{2} }}{4} \times L $$
(7)
$$ {\text{Volume}}\;{\text{by}}\;{\text{Smalian}}\;{\text{formula}} = \left( {\frac{{\frac{{\pi D_{1} ^{2} }}{4} + \frac{{\pi D_{2} ^{2} }}{4}}}{2}} \right) \times L $$
(8)
$$ {\text{Cone}}\;{\text{volume}} = \frac{{\pi D_{1} ^{2} }}{{12}} \times L $$
(9)

In these equations, D1 is the diameter at the thick end, D2 is the diameter at the thin end, and L is the length of the section.

Taper based volume

Since all the taper equations used in this study do not have a closed form, numerical integration was used to calculate the stem volume of each tree. This method was also followed by Poudel et al. (2018). The total length of the stem was divided into 100 equal sections. The diameters at two ends of those sections were predicted using the fitted taper model, and the volume of each section was calculated using Smalian’s formula. Total volume of the tree was obtained by adding the volume of all 100 sections.

Local volume model developed in this study

The stem volume of each tree was modelled as a function of DBH and total height (Eq. 10). A commonly used power function in the logarithmic form was fitted as this is recommended by several authors for predicting the volume of S. robusta in Nepal (Sharma and Pukkala 1990; Subedi 2017). Logarithmic transformation was used because such a model produced smaller residuals than the nonlinear model. The local volume model developed in this study was also validated using LOOCV method.

Volume equation of Sharma and Pukkala (1990)

Sharma and Pukkala (1990) developed a model using DBH (D) and total height (H) as variables to predict the stem volume of individual trees of S. robusta in the Nepalese forest (Eq. 11).

$$\mathrm{ln}\left(V\right)=-9.76124+1.86046\times \mathrm{ln}\left(D\right)+0.99067\times \mathrm{ln}\left(H\right)$$
(10)
$$\mathrm{ln}\left(V\right)=-24554+1.9026\times \mathrm{ln}\left(D\right)+0.8352\times \mathrm{ln}\left(H\right)$$
(11)

For comparison, we predicted the volume using the local volume model developed in this study (Eq. 10), taper equation developed in this study (M1), and models of Sharma and Pukkala (1990) (Eq. 11). Bias (Eq. 5) and RMSE (Eq. 4) were estimated and compared using these equations. The predicted volume was then plotted against DBH.

Results

Taper functions

The parameter estimates and fit statistics (R2, RMSE and AIC) for the seventeen taper functions evaluated in this study are presented in Table 3. Except for β1 of M16 and β2 of M17, all other parameters of the 17 taper functions were significant at 95% confidence level. Therefore, the taper functions M16 and M17were excluded from further analysis. Evaluation based on fit statistics showed that most of the remaining taper functions provided a strong fit except M15 which described only 80% of the variation in upper stem diameter with comparatively higher RMSE and AIC. Taper function M15 was also excluded from further analysis. The rest of the taper functions explained more than 96% of the variation in upper stem diameters. M1, M2, and M3 were selected as the best three as they provided higher values of R2 and lower RMSE and AIC values than other remaining taper functions.

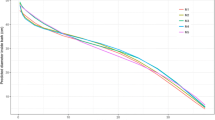
Table 3 Parameter estimates and fit statistics for different taper models used in this study
Full size table

The distribution of raw residuals against the predicted upper stem diameter and predictor variables (total height, height at which diameter was measured, and DBH) with a smooth superimposed curve for the three best taper functions (M1, M2 and M3) using tree-level random effect is presented in Fig. 2. Plot of residuals against the predicted upper stem diameter and predictor variables did not show any systematic trend in residual distribution. The taper function M1 performed the best with the highest R2 (0.99), lowest RMSE (0.57), and lowest AIC (1829). The graph of taper function M1 showed a minimum error with negligible curvature and outliers than other taper functions, suggesting the absence of local bias in this taper function. Therefore, M1 was selected as the best taper function to predict the upper stem diameters of individual trees of S. robusta. The predicted upper stem diameters at different tree heights using three best taper functions are presented in Fig. 3a. Stand density had a significant effect on the tapering of the stem of S. robusta (P < 0.05).

Fig. 2
figure 2

Distribution of residuals against the predicted upper stem diameter(a–c); total height (d–f); height at which diameter was measured (g–i); diameter at breast height (j–l) for the best three taper functions

Full size image
Fig. 3
figure 3

Predicted upper stem diameters at different heights using best three taper functions for a Shorea robusta with DBH 32.7 cm and height 26.8 m (a); leave-one-out cross-validation of taper model M1 (b); M2 (c); and M3 (d). R2 is coefficient of determination, RMSE is root mean squared error and MAE is mean absolute error. The dotted line in b–d is the 1:1 reference line

Full size image

Model validation

The fit statistics R2 and RMSE of the model fitted with validation data was similar with that of the model fitting data (Fig. 3b − d). The plot of predicted diameter against the observed diameter and predicted volume against observed volume further demonstrated that the developed taper and volume models are validated and able to predict upper stem diameters and volume with an acceptable level of accuracy.

Volume prediction

All parameter estimates of the fitted model were significant at a 99% confidence level. The model described more than 99% variation in the total volume of the individual tree (Eq. 10). Validation of this model (Eq. 10) also showed a similar fit statistic (Fig. 4a).

Fig. 4
figure 4

a Leave-one-out cross-validation of local volume model; b comparison of the local volume model with that predicted from the taper equation and Sharma and Pukkala (1990) model; c comparison of the predicted volume by the local volume model among three stand densities; and (d) comparison of the predicted volume by the best taper equation among three stand densities; R2 is coefficient of determination, RMSE is root mean squared error and MAE is mean absolute error; the dot line in a is the 1:1 reference line

Full size image

The volume calculated on destructive measurement was considered as a reference volume, and the volume predicted by the local volume model developed in this study, the taper equation developed in this study, and the model of Sharma and Pukkala (1990) were compared with the reference volume. Volume predicted by the local volume model and taper equation showed a positive bias, demonstrating that these two models underestimated the volume of S. robusta. Volume predicted by the Sharma and Pukkala (1990) model had a negative bias, demonstrating an over prediction. The local volume model showed a significantly smaller bias and RMSE compared to the other models (Table 4) and indicates that this model is more accurate in volume prediction. The difference in predicted volume among the models is smaller for small-sized trees and increased with size (DBH) of the tree (Fig. 4b).The predicted volume of individual trees differed significantly (P < 0.05) among three different stand densities (300, 400 and 500 trees per ha) (Fig. 4c, d).

Table 4 Mean bias and RMSE for predicting individual tree volume of Shorea robusta using volume model fitted in this study, taper equation, and Sharma and Pukkala (1990)
Full size table

Discussion

Seventeen taper functions were fitted and evaluated using data collected from 54 felled trees and the best model was selected for predicting upper stem diameters at a given height of S. robusta. The effect of stand density on taper was also examined. In addition, the actual volume of the individual sampled trees was compared with the volume predicted by the integration of the developed taper function, the local volume model and previously developed volume models for S. robusta in Nepal. The main findings indicate that the taper function of S. robusta developed using the tree-level random effect in mixed-effect modelling performed well for upper stem diameter prediction. It was also found that stem taper varied significantly with stand density. The merchantable and/or total stem volume of an individual tree can be predicted by integration of the taper function, but the accuracy of the predicted volume is lower compared to the stem volume predicted by the local volume model.

This study showed that the variable-exponent taper function of Sharma and Zhang (2004) performed best in predicting upper stem diameters for S. robusta. This has also been reported as the best function in predicting upper stem diameters of Chinese fir (Cunninghamia lanceolata (Lamb.) Hock.) in southern China (Duan et al. 2016). Several other studies have reported the better performance of variable exponent taper function in comparison to a single form and segmented taper functions (Sharma and Zhang 2004; Rojo et al. 2005; Duan et al. 2016). In contrast, other studies have shown that segmented taper functions are better than variable exponent taper functions (Crecente-Campo et al. 2009; Özçelik and Crecente-Campo 2016; Shahzad et al. 2021), suggesting that a particular form of the taper function may not be universally applicable.

Stand density has a significant effect on the tapering of individual trees of S. robusta. Growth in DBH and height of individual trees varies with stand density (Bhandari et al. 2021b). Diameter growth is more sensitive to a reduction in stand density than height. This indicates that diameter growth takes place more rapidly in a stand with low density than height. This results in variations in stem form and tapering of individual trees. Variation in stem form due to stand density may be explained by Metzger’s theory (Metzger 1893).Individual trees growing in an open stand allocate more resources towards the base of the tree to withstand external forces, including wind (Chaturvedi and Khanna 2011). Allocation of large amounts of resources towards the base of the tree results in a larger base and greater tapering. In contrast, trees growing in a dense stand face a relatively lower magnitude of external forces and avoid the unnecessary allocation of resources towards their base. Individual trees growing in dense stands do not receive sufficient light for growth compared to trees growing in less denser stands. Because of the limited availability of light, trees growing in the dense stands have a tendency of growing upward to receive more light. This results in less tapering and a more cylindrical stem. This study also showed a significant difference in individual tree volumes based on stand density. The difference in individual tree volume between 400 trees ha−1 and 500 trees ha−1 was relatively small but the difference between 300 and 500 trees ha−1 was relatively large (Fig. 4c). The difference between the average volume of trees in the stand with 300 trees ha−1 and with 500 trees ha−1 is statistically significant because the difference is > 20% (Table 1). The differences observed is for stands at age 33 years. As the size and age of the stand increase, the differences in volumes are expected to increase. Trees growing in lower stand density yield higher timber than trees in higher density stands. This will have significant implications in decision- making for forest managers, especially in timber production industries.

Taper functions for tree species of Nepal are limited. Only the taper function developed by Silwal et al. (2018) is available for S. robusta which used 33 trees from two different sites of the Terai region. Our study has used a relatively larger number of sample trees (n = 54). Data collected through destructive sampling is likely to improve accuracy more than data measured from the standing trees, although it increases the cost and time in data collection. Because of the higher accuracy of the data collected through destructive sampling, datasets generated from a small number of trees may be enough to develop the taper model and represent the whole population. Although the number of individual trees felled for data collection was 54, there were 756 data points to fit and evaluate the model. A mixed effect modelling approach was used to account for the correlation associated with multiple measurements taken from the same tree. The mixed effect modelling approach is more appropriate for repeatedly measured data (Lindstrom and Bates 1990).

This study showed that the volume predicted by the local volume model from the same forest and the general volume table developed for the whole of Nepal is more accurate than the volume predicted by the integration of the taper function. This indicates that the taper functions developed in this study are useful tools in predicting upper stem diameters but not in predicting the total stem volume of individual trees. Considering the poor performance of the taper function for total stem volume prediction, it is recommended using the local volume table for the prediction of total stem volume and taper function for the prediction of merchantable volume and/or volume up to a certain height for the stem and upper stem diameter. Poudel et al. (2018) also reported that the volume predicted by local volume models are more accurate than volumes predicted from taper functions developed for Douglas-fir and Western hemlock in the Pacific Northwest of the USA. In a study carried out in Mongolian oak (Quercus mongolica Fisch. ex Ledeb.) in South Korea, Ko et al. (2019) found a significant difference between the volume predicted by existing volume models and taper functions. They recommended using new taper equations to predict the volume by assuming that the forest condition and structure had been significantly changed since the preparation of the existing volume model.

Taper functions can be used as a tool in quantifying timber and other forest products, either from an individual tree or from a stand. These functions also serve as decision support tools in carbon trading and other ecosystem service estimations. Predicting upper stem diameter and stem volume of individual trees provides crucial information to prepare management plans or to implement those plans for sustainable forest management. As the taper function varies with species, stand densities, and management regimes, it is suggested that the development of taper function for each species and management regimes would achieve more accurate prediction and useful information for the sustainable management of forests.

Conclusions

This study developed a taper function using a non-linear mixed effect model for predicting upper stem diameters of S. robusta, the most important timber species in the southern lowlands of Nepal. The taper function of Sharma and Zhang (2004) performed the best in predicting upper stem diameter among the seventeen candidate functions studied. Stem taper of S. robusta varied with stand density. Although the taper function facilitated the prediction of upper stem diameter, total tree volume prediction was not as accurate as that obtained from the local volume equation. The developed taper functions can be used as a tool for estimating volume, biomass and carbon and can provide important information for the sustainable management of the most important commercial tree species (S. robusta) in Nepal. The taper model can be further improved by using data from many individual trees and a wider range of geographical regions and management regimes.