Skip to main content

Zentropy Theory for Positive and Negative Thermal Expansion

Journal of Phase Equilibria and Diffusion (2022)Cite this article

Abstract

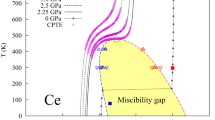
It has been observed in both natural and man-made materials that volume sometimes decreases with increasing temperature. Though mechanistic understanding has been gained for some individual materials, a general answer to the question “Why does volume sometimes decrease with the increase of temperature?” remains lacking. Based on the thermodynamic relation that the derivative of volume with respect to temperature, i.e., thermal expansion, is equal to the negative derivative of entropy with respect to pressure, we developed a general theory in terms of multiscale entropy to understand and predict the change of volume as a function of temperature, which is termed as zentropy theory in the present work. It is shown that a phase at high temperatures is a statistical representation of the ground-state stable and multiple nonground-state metastable configurations. It is demonstrated that when the volumes of the nonground-state configurations with high probabilities are smaller than that of the ground-state configuration, the volume of the phase may decrease with the increase of temperature in certain ranges of temperature-pressure combinations, depicting the negative divergency of thermal expansion at the critical point. As examples, positive and negative divergencies of thermal expansion are predicted at the critical points of Ce and Fe3Pt, respectively, along with the temperature and pressure ranges for abnormally positive and negative thermal expansions. The authors believe that the zentropy theory is applicable to predict anomalies of other physical properties of phases because the change of entropy drives the responses of a system to external stimuli.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price includes VAT (USA)
Tax calculation will be finalised during checkout.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

References

  1. C. Kittel, Introduction to Solid State Physics. John Wiley & Sons, New York, 2005.

    MATH  Google Scholar 

  2. A.W. Sleight, Isotropic Negative Thermal Expansion, Annu. Rev. Mater. Sci., 1998, 28, p 29–43.

    ADS  Article  Google Scholar 

  3. J.S.O. Evans, Negative Thermal Expansion Materials, J. Chem. Soc. Dalt. Trans., 1999, 19, p 3317–3326.

    Article  Google Scholar 

  4. G.D. Barrera, J.A.O. Bruno, T.H.K. Barron, and N.L. Allan, Negative Thermal Expansion, J. Phys. Condens. Matter, 2005, 17, p R217–R252.

    ADS  Article  Google Scholar 

  5. W. Miller, C.W. Smith, D.S. MacKenzie, and K.E. Evans, Negative Thermal Expansion: A Review, J. Mater. Sci., 2009, 44, p 5441–5451.

    ADS  Article  Google Scholar 

  6. C. Lind, Two Decades of Negative Thermal Expansion Research: Where Do We Stand?, Materials, 2012, 5(1125), p 1154.

    Google Scholar 

  7. R. Mittal, M.K. Gupta, and S.L. Chaplot, Phonons and Anomalous Thermal Expansion Behaviour in Crystalline Solids, Prog. Mater. Sci., 2018, 92, p 360–445.

    Article  Google Scholar 

  8. K. Takenaka, Progress of Research in Negative Thermal Expansion Materials: Paradigm Shift in the Control of Thermal Expansion, Front. Chem., 2018, 6, p 267.

    ADS  Article  Google Scholar 

  9. E. Liang et al., Negative Thermal Expansion: Mechanisms and Materials, Front. Phys., 2021, 16, p 53302.

    ADS  Article  Google Scholar 

  10. T.H.K. Barron, and G.K. White, Heat Capacity and Thermal Expansion at Low Temperatures. Kluwer Academic/Plenum, Boston, 1999.

    Book  Google Scholar 

  11. B. Fultz, Vibrational thermodynamics of materials, Prog. Mater. Sci., 2010, 55, p 247–352.

    Article  Google Scholar 

  12. L. Zhu, M. Garst, A. Rosch, and Q. Si, Universally Diverging Grüneisen Parameter and the Magnetocaloric Effect Close to Quantum Critical Points, Phys. Rev. Lett., 2003, 91, p 066404.

    ADS  Article  Google Scholar 

  13. P. Hohenberg, and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. B, 1964, 136, p B864–B871.

    ADS  MathSciNet  Article  Google Scholar 

  14. W. Kohn, and L.J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, p A1133–A1138.

    ADS  MathSciNet  Article  Google Scholar 

  15. N. Mardirossian, and M. Head-Gordon, Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals, Mol. Phys., 2017, 115, p 2315–2372.

    ADS  Article  Google Scholar 

  16. M.G. Medvedev, I.S. Bushmarinov, J. Sun, J.P. Perdew, and K.A. Lyssenko, Density Functional Theory is Straying from the Path Toward the Exact Functional, Science, 2017, 355, p 49–52.

    ADS  Article  Google Scholar 

  17. Vienna Ab-initio Simulation Package (VASP). https://www.vasp.at.

  18. Y. Wang, Z.K. Liu, and L.-Q. Chen, Thermodynamic Properties of Al, Ni, NiAl, and Ni3Al From First-Principles Calculations, Acta Mater., 2004, 52, p 2665–2671.

    ADS  Article  Google Scholar 

  19. Y. Wang, M.Q. Liao, B.J. Bocklund, P. Gao, S.L. Shang, H.J. Kim, A.M. Beese, L.Q. Chen, and Z.K. Liu, DFTTK: Density Functional Theory Toolkit for High-Throughput Lattice Dynamics Calculations, CALPHAD, 2021, 75, p 102355.

    Article  Google Scholar 

  20. Z.K. Liu, Y. Wang, and S. Shang, Thermal Expansion Anomaly Regulated by Entropy, Sci. Rep., 2014, 4, p 7043.

    Article  Google Scholar 

  21. M. Hillert, Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis. Cambridge University Press, Cambridge, 2008.

    MATH  Google Scholar 

  22. Z.K. Liu, and Y. Wang, Computational Thermodynamics of Materials. Cambridge University Press, Cambridge, 2016.

    Book  Google Scholar 

  23. Z.K. Liu, Computational Thermodynamics and its Applications, Acta Mater., 2020, 200, p 745–792.

    ADS  Article  Google Scholar 

  24. Z.K. Liu, S.L. Shang, and Y. Wang, Fundamentals of Thermal Expansion and Thermal Contraction, Materials (Basel), 2017, 10, p 410.

    ADS  Article  Google Scholar 

  25. Z.K. Liu, B. Li, and H. Lin, Multiscale Entropy and Its Implications to Critical Phenomena, Emergent Behaviors, and Information, J. Phase Equil. Diffus., 2019, 40, p 508–521.

    Article  Google Scholar 

  26. Z.K. Liu, L.Q. Chen, K.E. Spear, and C. Pollard, C. An Integrated Education Program on Computational Thermodynamics, Kinetics, and Materials Design. https://www.tms.org/pubs/journals/JOM/0312/LiuII/LiuII-0312.htmlhttps://www.tms.org/pubs/journals/JOM/0312/LiuII/LiuII-0312.html (2003).

  27. Y. Wang et al., Thermodynamics of the Ce Gamma-Alpha Transition: Density-Functional Study, Phys. Rev. B, 2008, 78, p 104113.

    ADS  Article  Google Scholar 

  28. Y. Wang et al., A Thermodynamic Framework for a System with Itinerant-Electron Magnetism, J. Phys. Condens. Matter, 2009, 21, p 326003.

    Article  Google Scholar 

  29. Y. Wang, S.L. Shang, H. Zhang, L.-Q. Chen, and Z.K. Liu, Thermodynamic Fluctuations in Magnetic States: Fe3Pt as a Prototype, Philos. Mag. Lett., 2010, 90, p 851–859.

    ADS  Article  Google Scholar 

  30. Liu, Z. K. Entropy. YouTube Video https://youtu.be/QZydut4y0hw (2021).

  31. DFTTK: Density Functional Theory Tool Kits. https://www.dfttk.org/.

  32. Z.K. Liu, Y. Wang, and S.-L. Shang, Origin of Negative Thermal Expansion Phenomenon in Solids, Scr. Mater., 2011, 65, p 664–667.

    Article  Google Scholar 

Download references

Funding

The work presented in this paper came from many projects supported by funding agencies in the United States in last two decades with the latest ones including the National Science Foundation (NSF, with the latest Grants CMMI-1825538 and CMMI-2050069), Department of Energy (with the latest Grants being DE-FE0031553, DE-NE0008945, DE-EE0008456, DE-SC0020147, and DE-AR0001435), NASA Space Technology Research Fellowship (with the latest Grant 80NSSC18K1168), Army Research Lab (with the latest Grant W911NF-14-2-0084), Office of Naval Research (with the latest Grant N00014-21-1-2608), Wright Patterson AirForce Base, NASA Jet Propulsion Laboratory, and the National Institute of Standards and Technology, plus a number of national laboratories and companies that supported the NSF Center for Computational Materials Design (NSF, 0433033, 0541674/8, 1034965/8), the Roar supercomputer at the Pennsylvania State University, the resources of NERSC supported by the Office of Science of the U.S. Department of Energy under contract No. DE-AC02-05CH11231, and the resources of XSEDE supported by NSF with Grant ACI-1053575. The authors would like to thank numerous collaborators over the years as reflected in the publications listed in ref. 23. ZKL would like to thank Josiah Roberts from University of Buffalo for suggesting the term zentropy during a seminar. The preparation of manuscript is partially supported by the Endowed Dorothy Pate Enright Professorship at The Pennsylvania State University. The proper copyrights for all the figures are granted by respective publishers.

Author information

Authors and Affiliations

  1. Department of Materials Science and Engineering, Pennsylvania State University, University Park, PA, 16802, USA

    Zi-Kui Liu, Yi Wang & Shun-Li Shang

Authors
  1. Zi-Kui Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shun-Li Shang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zi-Kui Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This invited article is part of a special tribute issue of the Journal of Phase Equilibria and Diffusion dedicated to the memory of former JPED Editor-in-Chief John Morral. The special issue was organized by Prof. Yongho Sohn, University of Central Florida; Prof. Ji-Cheng Zhao, University of Maryland; Dr. Carelyn Campbell, National Institute of Standards and Technology; and Dr. Ursula Kattner, National Institute of Standards and Technology.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Liu, ZK., Wang, Y. & Shang, SL. Zentropy Theory for Positive and Negative Thermal Expansion. J. Phase Equilib. Diffus. (2022). https://doi.org/10.1007/s11669-022-00942-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11669-022-00942-z

Keywords

  • entropy
  • negative thermal expansion
  • partition function
  • thermal expansion
  • thermal contraction
  • thermodynamics
  • zentropy