1 Introduction

Proposing a set of thermodynamic functions with a solid physical base to accurately describe the desired physical properties of materials is one of the targets of the Calphadians. To achieve this goal, efforts have been made to develop the third generation of thermodynamic databases based on the Einstein or Debye model of the heat capacity.[1,2,3,4] The descriptions of the pure elements, as the basis of the databases, have been evaluated using a combination of the Einstein/Debye model and polynomials or the segmented models.[5,6,7,8,9,10] The transition metals such as Fe, Co, Mn who occupy the center position of the periodic table are of special interest because many of them have intriguing magnetic properties. The magnetic heat capacity and magnetic Gibbs energy of most elements could be well described by the widely used Inden–Hillert–Jarl (I–H–J) model[11,12] while a few exceptional cases may not be. For this reason, Chen and Sundman applied the two-state magnetic model describing the magnetic properties of fcc iron to make sure the fcc Fe turn stable at 1185 K.[4] Before this, the two-state model has been introduced in the CALPHAD assessments by Kaufman[13] and Weiss[14] to model the magnetic behaviors of Fe, Mn and Cr. Miodownik has extended this model to the Fe-Ni-Cr ternary system.[15]

Co, as a member of the transition metals, also has anomalous magnetic property. There is a discrepancy between the value of the magnetic moment determined by the magnetic experiments (~ 1.7)[16,17,18,19,20] and the one derived from the thermochemical information (~ 1.3).[21,22] The value of previous one is too large to fit the peak of the magnetic heat capacity so the later one which is called ‘thermochemical moment’ was always preferred in the CALPAHD assessment. Miodownik suggested that the concept of two magnetic states might be a promising candidate to resolve this conflict.[23] Besides, ab initio calculations[24] indicated that there are two magnetic states in fcc cobalt which is similar to fcc iron, with the large volume, large magnetic moment state lying lower and the large volume, large magnetic one lying upper. Furthermore, Bendick and Pepperhoff[25] found similarities between pure fcc cobalt and fcc iron alloys experimentally by revealing their anomalies in electrical resistivity. These findings make it possible to introduce the two-state magnetic model to the pure Co. The use of the two-state magnetic model could provide more flexibility on assessing the magnetic properties of Co. In the present workwe employ the two-state magnetic model to describe the existence of two magnetic states in fcc Co. To resolve the discrepancy between two magnetic moment values, the value obtained by the magnetic experiments was accepted in the present assessment to fit the thermochemical data. A consistent thermodynamic description of pure Cowas achieved and the fit to the experimental data is reasonably good.

2 Thermodynamic Modeling

The thermodynamic models adopted in this work were firstly proposed in the 1995 Ringberg unary workshop[1,2,3,26] and then developed and applied to Fe by Chen and Sundman.[4] These new models provide a theoretical framework for the construction of the new generation of CALPHAD databases. Some assessments of the elements have been performed based on these models.[5,6,8] The Einstein model lays the foundation of the framework. The heat capacity of a solid substance can be described by its combination with the polynomials (see Eq 1).

$$C_{p} = 3R\left( {\frac{{\Theta_{E} }}{T}} \right)^{2} \frac{{e^{{\Theta_{E} /T}} }}{{\left( {e^{{\Theta_{E} /T}} - 1} \right)^{2} }} + aT + bT^{n} + C_{p}^{mag}$$
(1)

The first term on the right side is the main constitute of the heat capacity which represents the contribution from the Einstein model describing the harmonic vibration of the lattice. The theta denotes the Einstein temperature. The second and third terms indicate the contribution from the electronic excitation and the anharmonic vibration. The value of n could be chosen as 2, 3 or 4 depending on the shape of the heat capacity and it is possible to use two of them simultaneously if necessary. The magnetic heat capacity is described by the last term. The model for the magnetism used in the present work is a slightly revised version of the I-H-J model.[11,12] The details of this modified model could be found in the literature.[4,6] The Gibbs energy could be calculated from the heat capacity correspondingly (see Eq 2).

$$G = E_{0} + \frac{3}{2}R\theta_{E} + 3RT\ln \left[ {1 - \exp \left( { - \frac{{\theta_{E} }}{T}} \right)} \right] - \frac{a}{2}T^{2} - \frac{b}{n(n + 1)}T^{n + 1} - \int_{0}^{T} {\left[ {\int_{0}^{T} {\frac{{C_{p}^{mag} }}{T}} dT} \right]} dT$$
(2)

The sum of the first two terms on the right side describes the zero-point energy of the substance. The third one represents the contribution from the Einstein model. The fourth, fifth and sixth terms are derived from the second, third and fourth terms in Eq 1 respectively.

As mentioned in the introduction section, a two-state model[13,15,27] was applied to describe the magnetic properties of fcc Co. This model postulates that there are two states coexisting in one phase-one state with higher energy and another with lower. The energy gap between these two states is ΔE. The excitation between the two states could cause an extra contribution to the Gibbs energy which can be expressed as:

$$\Delta G^{2st} = - RT\ln \left( {1 + \frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{ - \Delta E}{RT}} \right)} \right)$$
(3)
$$\Delta E = A + BT$$
(4)

ΔE is the energy difference between the two states which is described as a function of temperature. g2/g1 indicates the degeneracy ratio of the two states. A and B are parameters to be optimized.

The contribution to the enthalpy and entropy could be written as:

$$\Delta H^{2st} = \frac{\Delta E}{{\frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{\Delta E}{RT}} \right) + 1}}$$
(5)
$$\Delta S^{2st} = R\left[ {\ln \left( {1 + \frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{ - \Delta E}{RT}} \right)} \right) + \frac{1}{{1 - \frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{\Delta E}{RT}} \right)}} \times \frac{\Delta E}{RT}} \right]$$
(6)

With increasing degeneracy ratio, the value of the enthalpy decreases while the entropy increases. The increase of the energy gap will lead to the increase of the enthalpy and the decrease of the entropy.

The contribution to the heat capacity could be represented as:

$$\Delta C_{p}^{2st} = R\left( {\frac{\Delta E}{RT}} \right)^{2} \frac{{\frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{\Delta E}{RT}} \right)}}{{\left[ {\frac{{g_{2} }}{{g_{1} }}\exp \left( {\frac{\Delta E}{RT}} \right) + 1} \right]^{2} }}$$
(7)

The shape of the heat capacity could be seen in Fig. 1. For the two-state magnetic model, it might be considered as a correction to the magnetic heat capacity described by the I–H–J model.[11,12] From the authors’ experiences, the value of the degeneracy ratio controls the height of the peak and the energy gap dominates the width of the peak.

Fig. 1
figure 1

The shape of the heat capacity attributed to the two-state model (Schottky anomaly)

Full size image

A generalized two-state model[2] was used for the modelling of the liquid-amorphous phase. In this model, the atoms can be occupied in either a liquid-like state or a solid-like state and the degeneracy ratio is set as 1. The liquid-like atoms have transitional degrees of freedom while the solid-like atoms have vibrational degrees. This hypothesis helps explain the phenomenon called ‘amorphous solidification’.[2] The Gibbs energy of the liquid-amorphous phase is thus defined as:

$$G^{liq - am} = {}^{o}G{}^{am} - RT\ln \left[ {1 + \exp ( - \Delta G_{d} /RT)} \right]$$
(8)

ΔGd is the energy gap between the liquid-like state and the solid-like state. oGliq-am and oGam could be thought of as the Gibbs energy of the phase when all the atoms were in each state. The thermodynamic function of oGam is identical to that of the solid phase except for the exclusion of the quartic term. ΔGd is written as follows:

$$\Delta G_{d} = A + BT + CT\ln T + \ldots$$
(9)

where A, B and C are the parameters to be assessed. B, referred to as the communal entropy, is suggested to set as a value comparable to − R which is the gas constant.

In the new models, an empirical method was designed to describe the temperature range which is above the melting temperature. The aim is to prevent the solid phase being stable again at very high temperature. This method can guarantee the consistency of the desired thermodynamic properties at the melting point thus a smooth curve in each property diagram. The details of this method were well demonstrated in Ref 4 and will not be discussed in this work.

3 Experimental Information and Optimization Procedure

The available experimental information on pure Co has been summarized in Ref 21, 28 and more recently in Ref 6. The experimental results accepted in the assessment[6] were also adopted in the present work except for (1) the value of the magnetic moment of each phase (2) the range of the hcp/fcc transition enthalpy and fcc/liquid transition enthalpy (3) the Curie temperature of the hcp phase. In this work, the value of beta for all stable phases of pure Co (hcp, fcc and liquid-amorphous phase) are set to 1.7 which fall within the range of magnetization measurement results.[16,17,18,19,20] In this work, the value 400 ± 40 J/mol for the enthalpy of hcp/fcc transition according to the Guillermet’s work[21] was accepted. The value 15,690 ± 1200, reported from the drop calorimetric data by Kubaschewski,[29] was adopted for the enthalpy of the fcc/liquid transition. The value of 1396 K, suggested by Guillermet,[21] was adopted as the Curie temperature for hcp phase. Due to the lack of available data, we accepted the degeneracy ratio value (1.35) of fcc Fe in Ref 4 and fixed the degeneracy ratio of fcc Co as the same value in the present work.

The assessment in the present work was performed using the PARROT module implemented in the Thermo-Calc software package.[30] As the stable phase at room temperature, the hcp phase was assessed firstly to fit the experimental heat capacity. Then the parameters of fcc phase were optimized based on the accepted experimental results on the heat capacity and hcp/fcc transition temperature and enthalpy. The assessment of the liquid-amorphous phase was finalized according to the adopted enthalpy and temperature of fusion.

4 Results and Discussions

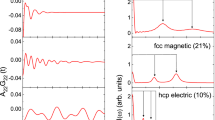
The model parameters optimized in the present work are listed in Table 1. The calculated heat capacity of hcp Co, compared with the SGTE description,[22] experimental data,[25,32,33,34,35,36,37,38] and the evaluated data[31] is plotted in Fig. 2. Two heat capacity curves are quite close at the temperature range from 300 to 1000 K. A good agreement with the experimental data was achieved. It could be seen from the figure that the peak of the magnetic heat capacity assessed in the present work is much higher than that of the SGTE description. The height of the peak was determined by the value of the magnetic moment (beta), one of two adjustable parameters in the I–H-J model,[11,12] and a larger beta value will lead to a higher peak. Another adjustable parameter, Curie temperature (Tc) controls the location of the peak. A detailed heat capacity curve from 0 to 300 K is showed together with the experimental data[32,33] and the evaluated data[31] in Fig. 3. The calculated result could reproduce the determined data points reasonably well. It is attributed to the adoption of the Einstein model where the Einstein temperature is the only parameter to be determined. The evaluated Einstein temperatures in this work are compared with the ones obtained from other sources in Table 2.[6,25,39,40,41,42] The Debye temperature that is more often found in the literature can be converted to the Einstein temperature by using a simple relation ϴE = 0.7143 ϴD.[43] The heat capacity curve of fcc Co is calculated and plotted together with the SGTE description,[20] the experimental data[25,33,34,36,37,38,44] and the assessed data[31] in Fig. 4. Although the present description has a higher peak at the magnetic transition temperature, its fit to the experimental data is comparable to the fit made by the SGTE description.[22] As mentioned above, there are only two adjustable parameters in the I–H–J magnetic model. This limitation makes it extremely difficult to fit the magnetic heat capacity with a much higher beta value just using the parameters in the I–H–J model.[11,12] The Fig. 5 shows the calculated magnetic heat capacity of fcc Co. The black solid line depicts the total magnetic heat capacity which consists of two parts. One part is the area below the red curve depicting the contribution from the two-state magnetic model. Another part is the area between the solid black line and the red line representing the magnetic heat capacity described by the I–H–J model. The latter part was plotted separately by the black dotted line to compare with the total magnetic heat capacity (the black solid line). From the comparison, it could be seen that the addition of the contribution from the two-state magnetic model considerably modifies the shape of the magnetic heat capacity. It changes the height and the width of the peak simultaneously without adjusting any parameters in the I–H–J model. In I–H–J model, the width of the peak is determined by a structure-dependent factor p whose value cannot be optimized during the assessment. The two-state magnetic model provides us additional flexibility to accommodate the experimental information on both magnetic moment and the magnetic heat capacity. It could be considered as a good complement for the I–H–J model[11,12] to describe the complicated magnetic properties of the materials. The calculated results indicates that the two-state magnetic model could be a promising way to resolve the discrepancy between the values of β for Co derived from the thermodynamic and magnetic routes.

Table 1 List of optimized parameters for the thermodynamic function of pure Co
Full size table
Fig. 2
figure 2

Calculated heat capacity of hcp Co (black solid line) compared with the experimental data,[25,32,33,34,35,36,37,38] evaluated data[31] and the SGTE description[22] (red dashed line) (Color figure online)

Full size image
Fig. 3
figure 3

Heat capacity of hcp Co (balck for the present work and red for the SGTE description[22]) from 0 to 300 K compared with the experimental data[32,33] and the evaluated data[31]

Full size image
Table 2 Estimated Einstein temperatures compared with the ones from other sources
Full size table
Fig. 4
figure 4

Heat capacity of fcc Co (black solid line) compared with the SGTE description[22] (red dashed line), the experimental data[25,33,34,36,37,38,44] and the evaluated data[31] (Color figure online)

Full size image
Fig. 5
figure 5

Calculated magnetic heat capacity of fcc phase. The black solid line represents the total magnetic heat capacity. The red line shows the contribution from the two-state magnetic model. The black dotted line depicts the contribution from the I–H–J model (Color figure online)

Full size image

Comparison between the calculated enthalpy of Co and the experimental data[35,36,37,38,45] as well as the evaluated data[31] is represented in Fig. 6. A good fit to the experimental data was obtained. The calculated entropy of Co was plotted together with the data points derived from the experimental determination[31,35] in Fig. 7. The entropy curve could reproduce the data very well. Some important thermodynamic properties calculated in the present work were summarized in Table 3.

Fig. 6
figure 6

The calculated enthalpy of Co (black for hcp, green for fcc and blue for liquid) compared with the experimental data[35,36,37,38,45] and the evaluated data[31]

Full size image
Table 3 List of several thermodynamic properties of pure Co
Full size table
Fig. 7
figure 7

The calculated entropy curve of Co (black for hcp, green for fcc and blue for liquid) compared with the entropy value derived from the experimental results[31,35]

Full size image

5 Conclusions

We applied the two-state magnetic model to the fcc Co to resolve the discrepancy between the magnetic moment derived from the thermochemical data and from the magnetic measurements. An updated description of pure Co was obtained for the third generation thermodynamic databases. The agreement between the calculated results and the experimental data was reasonably good. It indicates that the two-state magnetic model could be a promising candidate to complement the I–H–J model and to describe the complicated magnetic properties of the transition metals.