Thermodynamic Evaluation of the Co-Al-C System by Coupling Ab Initio Calculations and CALPHAD Approach

Abstract

The ternary Co-Al-C system was thermodynamically assessed using the CALPHAD method based on the critical review of all experimental information in the system. The κ-carbide was described with a three-sublattice model (Al,Co)₃(Al,Co)₁(C,Va)₁. To support the assessment, the enthalpies of formation of all end-members of the κ-carbide were studied by ab initio calculations. The solubility ranges of the carbon in the κ-carbide, the αCo and the AlCo (B2) phases were well reproduced. The equilibria involving the liquid phase were reasonably described using the present set of thermodynamic parameters.

1 Introduction

Ni-based superalloys exhibit an excellent combination of high-temperature strength, good oxidation and corrosion resistance due to the coherent precipitation of the ordered L1₂-type phase (γ′ Ni₃Al) within the face-centered cubic γ matrix.[1,2] Compared to Ni-based superalloys, the development of Co-based superalloys is subject to the absence of the coherent precipitate (γ′ Co₃Al) until recently Sato et al.[3] found the L1₂-type phase, Co₃(Al,W), with the addition of tungsten. An alternative development strategy has been attempting is to use some carbides such as κ-carbide as the strengthening phase with the introduction of carbon into the Co-based alloys. Mishima et al. have made great contributions on this subject.[4,5,6,7,8,9,10,11,12,13] The κ-carbide is an ordered cubic phase with perovskite E2₁-type structure, which is crystallographically similar to the L1₂ structure. In the present Co-Al-C system, the Al atoms occupy the cube corner, Co the face center and C the cube center, which depicts the metallic atoms form the L1₂-type lattice, while carbon occupies on the central octahedral interstitial site. Kimura et al.[5,6,10,13] reported that the Co-Al-C alloys with a large amount of κ-carbides show good compression strength and excellent ductility. Therefore, the knowledge of the phase equilibria involving the κ-carbide is indispensable for the design and development of this type of the Co-based superalloys. The thermodynamic investigation of the Co-Al-C system was performed by Ohtani et al.[14] combining the CALPHAD technique and ab initio calculations. Nevertheless, after their work, new experimental studies on the phase diagram of the Co-Al-C system were reported,[9,11,15] including the revision of the phase region of the κ-carbide[9,11] and the invariant reaction.[15] In addition, the updated description of the binary Al-Co system[16] also necessitates the re-assessment of the Co-Al-C system. More importantly, the ab initio calculations by Ohtani et al.[14] need to be improved. It was reported that their calculations were unreliable in another similar ternary Al-C-Fe system.[17,18] Therefore, new ab initio calculations were carried out at 0 K in the present work to assist the assessment of the κ-carbide. Using our ab initio calculations, the Co-Al-C system was assessed in the framework of the CALPHAD approach.

2 Binary Systems

2.1 Al-C

The Al-C binary is a simple system only including liquid, fcc-Al, graphite and Al₄C₃. The Al₄C₃ carbide forms from the peritectic reaction (liquid + (C) ↔ Al₄C₃) at 2429 K. Gröbner et al.[19] made a first assessment of the Al-C system, which is widely accepted so far. Actually, Ohtani et al.[14] re-assessed the binary to modify a slight deviation from the experimental carbon solubility in the liquid phase in the description by Gröbner et al.[19] However, the heat capacity of the Al₄C₃ phase above 1500 K assessed by Ohtani et al. differs from that by Gröbner et al. Connetable et al.[17] indicated that the experimental data in the ternary Al-C-Fe system did not support the modification of the Al₄C₃ phase. Additionally, based on the description by Gröbner et al., Connetable et al. slightly revised the fcc phase and introduced the metastable bcc phase. Therefore, the present work used the description by Gröbner et al.[19] with the revision by Connetable et al.[17] The calculated phase diagram of the Al-C system is shown in Fig. 1.

Fig. 1

Assessed Al-C phase diagram[17,19]

2.2 Al-Co

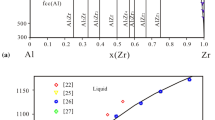
The Al-Co system is the most complex with six stoichiometric compounds on the Co-rich side and the ordered AlCo (B2) phase based on the bcc lattice in the middle part. All the stable phases in the system are summarized in Table 1 as well as their crystallographic information and thermodynamic models. This binary has been assessed several times.[16,20,21,22] Stein et al.[22] experimentally determined the melting behavior and homogeneity range of the AlCo phase for the first time and then thermodynamically assessed the Al-Co system. All reliable experimental data are well reproduced using their model parameters. Unfortunately, an inverse miscibility gap exists in the liquid phase above 4800 K, which was later eliminated by Wang et al.[16] Furthermore, Wang et al.[16] introduced the following three Al₁₃Co₄ phases, namely o-Al₁₃Co₄, m-Al₁₃Fe₄ and y-Al₁₃Fe₄, and considered the metastable ordered phase based on the fcc structure using the partitioning model. Thus, the description by Wang et al.[16] was adopted in the present work. The assessed phase diagram by Wang et al.[16] is shown in Fig. 2.

Table 1 Summary of the crystallographic information and thermodynamic models for the phases in the Co-Al-C system

Fig. 2

Assessed Al-Co stable phase diagram[16]

2.3 C-Co

The C-Co system is quite simple with the terminal phases of C and Co and the liquid phase. The thermodynamic assessment of this binary used in the present work was performed by Guillermet.[23] There are two invariant reactions: liquid ↔ αCo + (C) at 1594 K and αCo ↔ εCo + (C) at 695 K. The phase diagram calculated using the parameters in Ref 23 is shown in Fig. 3.

Fig. 3

Assessed C-Co phase diagram[23]

3 Experimental Information of the Ternary System

The experimental information on the Co-Al-C system are scarce. No investigation of the thermochemical properties in the ternary system is reported, except the formation enthalpies of the κ phase calculated by Ohtani et al.[14] using the Full Potential Linearized Augmented Plane Wave (FLAPW) method. However, their calculated formation enthalpies are more negative than those calculated in the present work. It should be mentioned that Ohtani et al.[24] using the same method also calculated the formation enthalpies of the κ phase in the Al-C-Fe system. It was found that their calculations deviate considerably from those reported in the literature[17,25,26] and those calculated by the present authors.[18] Therefore, the ab initio data by Ohtani et al.[14] were not adopted in the present optimization.

The experimental phase equilibria information are mainly investigated by Mishima’s group.[4,9,11] Before their work, Hütter et al.[27] investigated the isothermal section at 1173 K by metallographic examination and estimated the liquidus projection in the Co-rich corner. However, their data were not confirmed in the later studies by Kimura et al.[4,9] Kimura et al.[4] investigated the phase equilibria of the Co-Al-C alloys. The alloys were annealed at 1373 K for 30 h. The phase identification and microstructures were studied using optical microscope (OM), transmission electron microscope (TEM), scanning electron microscope (SEM) and x-ray diffraction analysis (XRD). Unfortunately, the carbon content in each phase was not accurately measured due to the difficulty in analyzing the local composition of carbon with energy dispersive x-ray spectroscopy (EDS). According to the measured phase equilibria, Kimura et al.[4] constructed the isothermal section of the ternary system on the Co-rich corner at 1373 K. The κ-carbide has more than 13.52 at.% solubility of carbon. By means of differential thermal analysis (DTA), the liquidus projection was also determined in their work as well as three isoplethal sections at constant C or Al content. The κ-carbide was found to take part in the three invariant reactions. Later, Kimura et al.[9] re-investigated the phase equilibria involving the κ phase using TEM, SEM, XRD and electron probe microanalysis (EPMA). The compositions of the phases in equilibrium were measured with wavelength dispersive x-ray spectroscopy (WDS). The phase boundary of the three-phase (κ/αCo/AlCo) field at 1373 K was determined. It should be noted that the carbon solubility in the κ-carbide in equilibrium with the αCo and AlCo phases reported by Kimura et al.[9] is lower than that obtained in their previous work.[4] Using optical floating zone melting, a single crystal of the κ-carbide was produced at the composition of Co-20.6Al-12.7C (at.%). This composition locates in the three-phase (κ/αCo/AlCo) equilibrium field according to their previous work.[4] Furthermore, the liquid composition of the invariant reactions were slightly revised, resulting in a slight modification of the liquidus projection in the previous work.[4] Maruoka and Suzuki[11] measured the phase equilibria of the Co-Al-C alloys with high carbon contents. The alloys were annealed at 1473 K for 72 h and analyzed using SEM–EDS and XRD. Although the single κ phase was not obtained, the homogeneity range of the κ-carbide was estimated to be very narrow.

In addition, Fritscher and Welsch[15] studied the solidification microstructure and transformation temperature of Co-Al-C alloys using OM and DTA. They indicated that the invariant reaction of the four-phase liquid/κ/αCo/AlCo in the work of Kimura et al.[4,9] should be eutectic, i.e. liquid ↔ κ + αCo + AlCo. Accordingly, the liquidus projection and reaction scheme of the Co-Al-C system were revised in their work.[15]

4 Thermodynamic Modelling

All phases were modelled in the framework of the Compound Energy Formalism (CEF)[28] in the present work, as summarized in Table 1. All the thermodynamic calculations and optimization in the present work were performed with the Thermo-Calc software.[29] The thermodynamic descriptions of the pure elements were directly taken from the SGTE compilation by Dinsdale.[30] The present optimized thermodynamic parameters are summarized in Table 2.

Table 2 Thermodynamic parameters optimized in the present work

4.1 Liquid

The liquid phase was described as a substitutional solution in the present work. The molar Gibbs energy of the liquid phase can be calculated by:

$$G_{m}^{\text{liq}} = \sum\limits_{i} {x_{i}{^{o} G_{i}}^{\text{liq}} } + RT\sum\limits_{i} {x_{i} \ln (x_{i} )} +{^{E}G_{m}^{\text{liq}}}$$

(1)

where $^{o} G_{i}^{\text{liq}}$ and $x_{i}$ are the molar Gibbs energy in the liquid state and the mole fraction of pure element $i$, respectively. R and T are the gas constant and the absolute temperature, respectively. The molar excess Gibbs energy $^{E} G_{m}^{\text{liq}}$ describes the deviation from ideal mixing, given as:

$$^{E} G_{m}^{\text{liq}} = \sum\limits_{i} {\sum\limits_{j > i} {x_{i} x_{j} L_{i,j}^{\text{liq}} } } + \sum\limits_{i} {\sum\limits_{j > i} {\sum\limits_{k > j} {x_{i} x_{j} x_{k} L_{i,j,k}^{\text{liq}} } } }$$

(2)

The first and second terms on the right hand side represent the contribution to the excess Gibbs energy from the binary interaction and the ternary interaction, respectively. No modifications on the constituent binary systems were made in the present work, i.e. the binary interaction parameters were taken from the descriptions in Ref 16, 19 and 23. According to Hillert,[31] the ternary interaction parameter $L_{i,j,k}^{\text{liq}}$ may be composition dependent:

$$L_{i,j,k}^{\text{liq}} = v_{i} {}^{i}L_{i,j,k}^{\text{liq}} + v_{j} {}^{j}L_{i,j,k}^{\text{liq}} + v_{k} {}^{k}L_{i,j,k}^{\text{liq}}$$

(3a)

$$v_{i} = x_{i} + {{(1 - x_{i} - x_{j} - x_{k} )} \mathord{\left/ {\vphantom {{(1 - x_{i} - x_{j} - x_{k} )} 3}} \right. \kern-0pt} 3}$$

(3b)

$$v_{j} = x_{j} + {{(1 - x_{i} - x_{j} - x_{k} )} \mathord{\left/ {\vphantom {{(1 - x_{i} - x_{j} - x_{k} )} 3}} \right. \kern-0pt} 3}$$

(3c)

$$v_{k} = x_{k} + {{(1 - x_{i} - x_{j} - x_{k} )} \mathord{\left/ {\vphantom {{(1 - x_{i} - x_{j} - x_{k} )} 3}} \right. \kern-0pt} 3}$$

(3d)

In the present work of the Co-Al-C system, the ternary parameter is given as:

$$L_{\text{Al,C,Co}}^{\text{liquid}} = x_{\text{Al}} {}^{\text{Al}}L_{\text{Al,C,Co}}^{\text{liquid}} + x_{\text{C}} {}^{\text{C}}L_{\text{Al,C,Co}}^{\text{liquid}} + x_{\text{Co}} {}^{\text{Co}}L_{\text{Al,C,Co}}^{\text{liquid}}$$

(4)

4.2 Solid Solution Phases

There are two stable solid solution phases (fcc_A1 and hcp_A3) and one metastable phase (bcc_A2) in the Co-Al-C system. Accounting for the interstitial element, i.e. carbon, the two-sublattice model was adopted for these phases. The metallic atoms occupy the substitutional sublattice, while carbon and vacancy occupy the interstitial sublattice. Accordingly, the model reads (Al,Co)_a(C,Va)_c, where a and c denote the number of sites on each sublattice, as listed in Table 1. However, the model for the bcc_A2 phase was extended from (Al,Co)₁(C,Va)₃ to (Al,Co,Va)₁(C,Va)₃, since vacancies were introduced onto the first sublattice in the evaluation of the Al-Co system by Wang et al.[16] The molar Gibbs energy of the bcc_A2 phase can be expressed as:

$$G_{m}^{A2} = \sum\limits_{{i = {\text{Al,Co,Va}}}} {\sum\limits_{{j = {\text{C,Va}}}} {y_{i}^{{\prime }} y_{j}^{{{\prime \prime }}} {^{o}G_{i:j}^{A2} }} } + RT\left[ {\sum\limits_{{i = {\text{Al,Co,Va}}}} {y_{i}^{{\prime }} \ln (y_{i}^{'} )} + 3\sum\limits_{{j = {\text{C,Va}}}} {y_{j}^{{\prime \prime }} \ln (y_{j}^{''} )} } \right] + {}^{\text{mag}}G_{m}^{A2} + {}^{E}G_{m}^{A2}$$

(5)

where $y_{i}^{'}$ and $y_{j}^{''}$ are the site fraction of $i$ on the first sublattice and $j$ on the second sublattice, respectively. $^{o} G_{i:j}^{A2}$ is the Gibbs energy of the end-member $ij_{3}$ and taken from the binary descriptions.[16,17,23] Particularly, the Gibbs energy of the end-member VaC₃ was set to 500,000 J/mol higher than that of graphite in the present work. ${}^{\text{mag}}G_{m}^{A2}$ is the Gibbs energy contribution due to magnetism, expressed as[32]:

$${}^{\text{mag}}G_{m}^{A2} = RTf(\tau )\ln (\beta + 1)$$

(6a)

$$f(\tau < 1) = 1 - \frac{1}{A}\left( {\frac{{79\tau^{ - 1} }}{140p} + \frac{474}{497}\left( {\frac{1}{p} - 1} \right)\left( {\frac{{\tau^{3} }}{6} + \frac{{\tau^{9} }}{135} + \frac{{\tau^{15} }}{600}} \right)} \right)$$

(6b)

$$f(\tau > 1) = - \frac{1}{A}\left( {\frac{{\tau^{ - 5} }}{10} + \frac{{\tau^{ - 15} }}{315} + \frac{{\tau^{ - 25} }}{1500}} \right)$$

(6c)

where $\tau = \frac{T}{{T_{\text{C}} }}$ and $A = \frac{518}{1125} + \frac{11692}{15975}\left( {\frac{1}{P} - 1} \right)$. $\beta$ is the average magnetic moment and $T_{\text{C}}$ the Curie temperature. $p$ is 0.40 for bcc structure or 0.28 for other structures.

In the present work, the molar excess Gibbs energy ${}^{E}G_{m}^{A2}$ for the bcc_A2 phase is calculated by:

$$\begin{aligned} {}^{E}G_{m}^{A2} = & y_{\text{Al}}^{{\prime }} y_{\text{Co}}^{{\prime }} y_{\text{Va}}^{{\prime \prime }} L_{{{\text{Al}},{\text{Co}}:{\text{Va}}}}^{A2} + y_{\text{Al}}^{{\prime }} y_{\text{Va}}^{{\prime }} y_{\text{Va}}^{{\prime \prime }} L_{{{\text{Al}},{\text{Va}}:{\text{Va}}}}^{A2} + y_{\text{Co}}^{{\prime }} y_{\text{Va}}^{{\prime }} y_{\text{Va}}^{{\prime \prime }} L_{\text{Co,Va:Va}}^{A2} + y_{\text{Al}}^{{\prime }} y_{\text{C}}^{{\prime \prime }} y_{\text{Va}}^{{\prime \prime }} L_{\text{Al:C,Va}}^{A2} \\ \, +\,y_{\text{Al}}^{{\prime }} y_{\text{Co}}^{{\prime }} y_{\text{C}}^{{\prime \prime }} L_{\text{Al,Co:C}}^{A2} \\ \end{aligned}$$

(7)

where the first four interaction parameters were taken from the evaluation of the binary systems.[16,17] It should be noted that the metastable bcc_A2 phase is the disordered part of the AlCo (B2) phase. Since no systematic study of the effect of the carbon on the metallic ordering is reported, the present work introduced the interaction parameters $L_{\text{Al,Co:C}}^{A2}$ into the disordered part to describe the narrow carbon solubility range of the AlCo phase. By adding the contribution due to the chemical ordering, the Gibbs energy of the AlCo (B2) phase is expressed as:

$$G_{m}^{B2} = G_{m}^{A2} (x_{i} ) + \Delta G_{m}^{\text{ord}}$$

(8a)

$$\Delta G_{m}^{\text{ord}} = G_{m}^{\text{ord}} (y_{i} ) - G_{m}^{\text{ord}} (y_{i} = x_{i} )$$

(8b)

where $\Delta G_{m}^{\text{ord}}$ represents the ordering contribution to the Gibbs energy. The ordering contribution becomes zero, when the phase is disordered.

4.3 κ-Carbide

In the present work, the κ-carbide was described using a simplified ordinary sublattice model, i.e. (Al,Co)₃(Al,Co)₁(C,Va)₁, compared to the complex five-sublattice partitioning model used in the Al-C-Fe[18] and Al-C-Mn[33] systems. Despite its simplicity, the present model is capable to describe the ordering of metallic atoms, i.e. the occupation of Co on the Al sites as well as Al on the Co sites. The introduction of vacancies onto the interstitial sublattice makes the model applicable in wider composition range of non-stoichiometry of carbon. Although this model does not reflect the potential second order phase transition from the disordered state to the ordered state between the metallic atoms, the number of the model parameters is significantly reduced. The Gibbs energy of the κ-carbide can be expressed as:

$$\begin{aligned} G_{m}^{\kappa } = & \sum\limits_{{i = {\text{Al,Co}}}} {\sum\limits_{{j = {\text{Al,Co}}}} {\sum\limits_{{k = {\text{C,Va}}}} {y_{i}^{'} y_{j}^{''} y_{k}^{'''} {^{o}G_{i:j:k}^{\kappa }} } } } \\ \, \quad + RT\left[ {3\sum\limits_{{i = {\text{Al,Co}}}} {y_{i}^{'} \ln (y_{i}^{'} )} + \sum\limits_{{j = {\text{Al,Co}}}} {y_{j}^{''} \ln (y_{j}^{''} )} + \sum\limits_{{k = {\text{C,Va}}}} {y_{k}^{'''} \ln (y_{k}^{'''} )} } \right] + {}^{E}G_{m}^{\kappa } \\ \end{aligned}$$

(9)

where $^{o} G_{i:j:k}^{\kappa }$ is the compound energy of the end-member (i)₃(j)₁(k)₁. In the present work, these end-member parameters are divided into three types based on the optimization. The first type includes $^{o} G_{\text{Al:Al:Va}}^{\kappa }$ and $^{o} G_{\text{Co:Co:Va}}^{\kappa }$, which were set to 5000 J/mol higher than the Gibbs energy of the Al and Co in the fcc state, respectively. The second type is $^{o} G_{\text{Al:Co:C}}^{\kappa }$, which was derived from the relationship:

$${^{o} G_{\text{Al:Co:C}}^{\kappa }} +{^{o} G_{\text{Co:Al:C}}^{\kappa }} ={^{o} G_{\text{Co:Co:C}}^{\kappa }} +{^{o} G_{\text{Al:Al:C}}^{\kappa }}$$

(10)

The third type for the rest of parameters were optimized based on the enthalpies of formation calculated by ab initio calculations. For the excess Gibbs energy ${}^{E}G_{m}^{\kappa }$, only one interaction parameter was introduced, given as ${}^{E}G_{m}^{\kappa } = y_{\text{Al}}^{'} y_{\text{Co}}^{'} y_{\text{Al}}^{''} y_{\text{C}}^{'''} L_{\text{Al,Co:Al:C}}^{\kappa }$, to account for the limited experimental data of this Co-Al-C system.

5 Ab Initio Calculations

In the present work, the projector augmented wave (PAW) method[34,35] as implemented in the Vienna ab initio simulation package (VASP)[36,37,38] was used to obtain total energies of reference states elements and ordered structures. The calculations were performed using the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA).[39] All of the structures were fully relaxed and performed with full spin polarization. The convergence criteria for the total energy was 10⁻⁶ eV/cell, while the criteria for force during structural optimization was 9 × 10⁻³ eV/Å. Plane waves up to 600 eV were included in the VASP-PAW calculations. The Monkhorst–Pack scheme[40] with a k-mesh of 20 × 20 × 20 in the Brillouin zone was used to generate k-points for the E2₁ and L1₂ structures.

The enthalpies of formation of the end-members of the κ-carbide were derived from the total energies from ab initio calculations, i.e.

$$\Delta_{f} H_{{{\text{Co}}_{x} {\text{Al}}_{y} {\text{C}}_{z} }} \approx E_{{{\text{Co}}_{x} {\text{Al}}_{y} {\text{C}}_{z} }} - \left[ {\frac{x}{x + y + z}E_{\text{Co}} + \frac{y}{x + y + z}E_{\text{Al}} + \frac{z}{x + y + z}(E_{\text{C}} - 1.895{\text{ kJ}})} \right]$$

(11)

where $E_{{{\text{Co}}_{x} {\text{Al}}_{y} {\text{C}}_{z} }}$, $E_{\text{Co}}$, $E_{\text{Al}}$ and $E_{\text{C}}$ are the total energies for the E2₁ structure ${\text{Co}}_{x} {\text{Al}}_{y} {\text{C}}_{z}$, hcp cobalt, fcc aluminum and diamond carbon, respectively. x, y and z are the numbers of atoms of Al, Mn, and C, respectively. The diamond carbon was calculated due to the difficulty in calculating van der Waals energy in graphite using the conventional exchange–correlation functional.[41] The value (1.895 kJ) is the enthalpy of carbon in the diamond state with respect to the graphite state, which has been used in Ref 18, 25 and 33.

6 Result and Discussion

6.1 Ab Initio Calculations

The formation enthalpies of the end-members of the κ-carbide calculated by ab initio calculations are shown in Table 3 together with the calculated results by Ohtani et al.[14] Apparently, the formation enthalpy of E2₁-Co₃AlC in Ref 14 is much lower than that in the present work, which is analogous to the comparison in the Al-C-Fe system,[18] as stated in section 3. For the reason, the calculated enthalpies by Ohtani et al.[14] were not used in the present optimization.

Table 3 Formation enthalpies of the κ-carbide at 0 K from ab initio calculations

For the end-member compounds E2₁-Co₃AlC and E2₁-CoAl₃C, two configurations for each compound were considered in the calculations. The configurations are illustrated in Fig. 4 and their corresponding enthalpy values are listed in Table 3. It can be seen that the configuration I and III have lower energy than those of configuration I and IV, which implies that the cube corner sites are preferentially occupied by aluminum atoms. Combining with the calculated results in the Al-C-Fe[18] and Al-C-Mn[33] systems, it can be concluded that aluminum atoms are preferentially at the cube corner in contrast to the transition elements due to the carbon. It should be mentioned that the formation enthalpies of all the E2₁-type compounds, except the E2₁-Co₃AlC, are very positive, which leads to a very small homogeneity range of the κ-carbide with respect to Al, as shown in Fig. 7.

Fig. 4

Possible configurations of E2₁ structure with the calculated formation enthalpies: (a) configuration I and (b) configuration II for the E2₁-Co₃AlC compound; (c) configuration III and (d) configuration IV for the E2₁-CoAl₃C compound

6.2 Thermodynamic Optimization

The enthalpies of formation of all end-members of the κ-carbide at 298 K calculated using the present model parameters are compared with those from ab initio calculations. It can be seen in Fig. 5 that an excellent agreement is achieved. Apparently, the enthalpy value of the E2₁-Co₃AlC compound calculated by Ohtani et al.[14] is much lower than the present results both from CALPHAD calculations and ab initio calculations. Figure 6 presents the site fractions of Al and C in the κ-carbide with the variation of carbon content at 1373 K. It can be seen that at the stoichiometric composition of Co₃AlC, the site fraction of Al is zero in the first sublattice and unity in the second sublattice. According to the present model (Al,Co)₃(Al,Co)₁(C,Va)₁, it actually reflects that the first and second sublattices are fully occupied by Co and Al, respectively. Removing C from the Co₃AlC system results in anti-site defects of metallic atoms, i.e. small fraction of Al replace Co in the first sublattice, while small fraction of Co replace Al in the second sublattice.

Fig. 5

Enthalpies of formation of the κ-carbide at 298 K together with the ab initio data

Fig. 6

Calculated site fractions of Al (in the sublattice 1 and 2) and C (in the sublattice 3) in the κ-carbide at 1373 K

Figure 7 shows the calculated isothermal sections in the Co-rich part at 1373 and 1473 K together with the experimental data[4,9,11] and the calculation results by Ohtani et al.[14] Since the composition analysis of the carbon has a relatively large uncertainty at lower content even using EPMA, the calculated carbon solubility in the AlCo phase was accepted. As mentioned in the previous section, the Al solubility range in the κ-carbide is narrow due to the quite positive formation enthalpies of the end-members such as E2₁-CoAl₃C and E2₁-Al₄C in contrast to that of E2₁-Co₃AlC. It should be pointed out that the κ-carbide is more close to the stoichiometric composition Co₃AlC with the decreasing temperature. Relative to the calculation results by Ohtani et al.,[14] the present calculated composition ranges of the κ-carbide and αCo phase are larger. It can also be seen that the present calculation agrees better with the experimental data.[9] In the description of Ohtani et al.,[14] the liquid phase is stable at 1473 K at the composition of approximate Co-16.8Al-4.3C and Co-8.5Al-9.4C (at.%), as shown in Fig. 7(b) with green arrows, which is inconsistent with the experimental data.[11]

Fig. 7

Calculated isothermal sections of the Co-Al-C system at (a) 1373 K and (b) 1473 K by the present work and Ohtani et al.[14] The experimental data are from Ref 4, 9 and 11

The isoplethal sections at 3 at.% C, 10 at.% C and 30 at.% Al are plotted in Fig. 8 using the present thermodynamic parameters. The corresponding calculation results from Ohtani et al.[4] and experimental data are overlapped in the figure. A reasonable agreement between the present description and the experimental results[4] is achieved. The temperature of the invariant reaction between the liquid, κ-carbide, αCo and AlCo phases is 1471 K in the evaluation of Ohtani et al.[14] which largely deviates from the experimental value (1616 K)[4] as shown in Fig. 8(a) and (b).

Fig. 8

Calculated isoplethal sections of the Co-Al-C system at (a) 3 at.% C, (b) 10 at.% C and (c) 30 at.% Al by the present work and Ohtani et al.[14] The experimental data are from Ref 4

The predicted liquidus projection in the Co-rich part of the Co-Al-C system is shown in Fig. 9 together with the experimental composition point of the invariant reactions[4,9,15] and the primary phase information.[15] The calculated primary κ-carbide solidification region in the previous work[14] is much larger than the experimental data and that in the present work. Nevertheless, the present assessment does not give a perfect agreement with the experimental primary κ-carbide phase region, especially the carbon content for the invariant reactions. It is attributing to the compromise between the liquidus projection and the isoplethal sections. Considering the relatively large uncertainty of the carbon composition analysis in comparison with the temperature measurement, the present set of thermodynamic description is accepted. Moreover, the reaction temperatures in the present work agree much better with the experimental values than those in the previous work,[14] as presented in Table 4.

Fig. 9

Calculated liquidus projection in the Co-rich part of the Co-Al-C system by the present work and Ohtani et al.[14] The experimental data are from Ref 4, 9 and 15

Table 4 Invariant reactions in the Co-Al-C system

7 Conclusions

In the present work, the thermodynamic assessment of the Co-Al-C system was performed within the framework of CALPHAD approach. In order to better assess the κ-carbide, the enthalpies of formation of all end-members of the κ-carbide were studied by ab initio calculations. A simplified model, i.e. (Al,Co)₃(Al,Co)₁(C,Va)₁, was adopted for the κ-carbide with less parameters compared with the five-sublattice model. Isothermal and isoplethal sections were calculated and fitted to the experimental data. The homogeneity ranges of the κ-carbide, αCo and AlCo phases were reasonably reproduced as well as the liquidus projection.