Introduction

Cluster expansions (CEs) have become a ubiquitous tool in computational alloy theory[1–21] and even in seemingly completely unrelated fields such and electronic band gap engineering and protein sequencing.[22–25] It is used to express thermodynamic and other properties as function of the configurational order of alloys. Most of the applications focus on binary alloys. However, the most interesting and the most realistic alloys are generally multi-component alloys. Although there are several CE studies on ternary alloys,[26–32] usually a presupposed cluster, such as the irregular tetrahedron in the case of bcc lattices, is selected while ignoring convergence issues. On the other hand, more recent ab initio studies on multinary alloys are not so clear on the formal basis and the actual implementation of the CE[33,34,19,35,36] so that a comprehensive derivation, such as given here, might be desirable. In particular, the generalized Ising model for binary alloys cannot be extended easily to multinary alloys.[37] The specific treatment in the literature of vacancy mediated diffusion in alloys[21, 38, 39] too, is scant and not very detailed on practical implementation. In the current work we try to present a comprehensive and detailed formalism that trivially extends to multi-component alloys. An important special feature is that CEs for multinary systems can be built-up from expansions with fewer components. We will first define a general framework for substitutional alloys, next describe how to add atomic species to a CE with re-use of already determined expansion coefficients. Then a generalization of the cluster expansion to treating the environmentally dependent energetics of transition states for vacancy mediated diffusion in concentrated alloys will be presented. Finally some applications to multi-components alloys are presented as illustrations.

Theory

Cluster Probabilities, Sum Rules, and Correlation Functions

Here, without loss of generality, we will assume that the expanded property is the energy \(E\). The CE assumes that the energy can be written as a rapidly converging sum over cluster contributions where contributions from larger clusters become negligible. A practical example of this idea is common in organic chemistry where the formation enthalpy of a molecule can be expressed approximately as a sum of contributions from nearest neighbor pairs (read bonds) only. In the case of ethane one would count one C-C pair and six C-H pairs and estimate that the formation energy with respect to the isolated atoms is given as the sum of the single C-C bond energy and the six C-H bond energies. Contributions from larger clusters such as triplets usually provide minor corrections only. We will now return to the case of crystalline bulk alloys and limit ourselves to the case where every atom can be uniquely identified with one and only one atomic position. That is, the alloy becomes perfectly periodic with a relatively small unit cell when all atoms were to become indistinguishable. There is a well-defined “fixed” underlying grid of atomic sites. In such a case clusters can be uniquely identified without any ambiguity on how to classify any group of atomic sites. There would then never be any doubt whether a given pair is a 1st or a 2nd nearest neighbor pair. Another aspect of a “fixed underlying grid is that the configuration of the alloy would be completely specified by the atomic occupation for every site, as in the case of e.g. the Ising model. In analogy with the Ising model we could assign the occupation of every site with a site occupation variable,

$$\upsigma_{i}^{(P)} = \left\{ {\begin{array}{*{20}l} 1 \hfill & { \, P\;{\text{atom}}\;{\text{at}}\;{\text{site}}\;i} \hfill \\ 0 \hfill & {{\text{ no}}\;P\;{\text{atom}}\;{\text{at}}\;{\text{site}}\;i} \hfill \\ \end{array} } \right.,$$

where \(P\) designates a particular atomic species, the parentheses remind us it does not refer to exponentiation.[40,41,32] To be completely general we will consider a vacancy also as an atomic species. If there are \(N\) atomic species in the alloy, only \(N - 1\) need to be specified because of a sum rule:

$$\sum\limits_{P = 1}^{N} {\upsigma_{i}^{(P)} } = 1\quad \forall i.$$

It signifies that every site is occupied by one and only one atom. The occupation of an arbitrary pair cluster consisting of sites \(i\) and \(j\) with occupations \(P\) and \(Q\) can be described in terms of site occupation variables

$$\upsigma_{ij}^{(PQ)} =\upsigma_{i}^{(P)}\upsigma_{j}^{(Q)} .$$

Here again, sum rules apply for every individual pair

$$\sum\limits_{P = 1}^{N} {\sum\limits_{Q = 1}^{N} {\upsigma_{ij}^{(PQ)} } } = 1\quad \forall ij\quad {\text{and}}\quad \sum\limits_{P = 1}^{N} {\upsigma_{ij}^{(PQ)} } =\upsigma_{j}^{(Q)} .$$

Therefore, it is necessary to only specify the \(N - 1\) occupations of sites \(i\) and \(j\) and to only specify the pair occupations that contain exclusively the \(N - 1\) atomic species in order to fully designate the specific atomic occupancy of the \(ij\) pair cluster. It is not necessary to specify the occupation of a point or pair cluster that contains one or more atoms of type \(N\). This generalizes to clusters of multiple sites: a three body cluster consisting of sites \(i\), \(j\), \(k\) with occupations \(P\), \(Q\), \(R\) can be described in terms site occupation variables

$$\upsigma_{ijk}^{(PQR)} =\upsigma_{i}^{(P)}\upsigma_{j}^{(Q)}\upsigma_{k}^{(R)} .$$

The value of any \(\upsigma_{ijk}^{PQR}\) where an \(N\) type atom occurs follows from sum rules and occupations of contained points, contained pairs, and triangle involving \(N - 1\) species exclusively.

The specific occupation of any particular cluster is generally not of interest in an infinitely large crystal. Then, the cluster probabilities are much more informative. Cluster probabilities are averages over equivalent clusters, where equivalence derives from the symmetry of the underlying grid of atomic sites. Angle brackets are used to designate cluster probabilities. \(\left\langle {\upsigma_{ij}^{PQ} } \right\rangle\) with sites \(i\) and \(j\) nearest neighbors, thus indicates the probability that any nearest neighbor pair in the infinite crystal is occupied by a \(PQ\) pair of atoms. Obviously, this probability shall always be in the interval [0,1]. The previously mentioned sum rules also apply to cluster probabilities so that probabilities exclusively pertaining to the \(N - 1\) atomic species only are needed for a full description of probabilities. In other words, the cluster probabilities pertaining to \(N - 1\) atomic species present a complete set of independent basis functions of the alloy configuration. Therefore, unlike the complete set of cluster probabilities involving all \(N\) atomic species, the subset of the cluster probabilities pertaining to the \(N - 1\) atomic species is a suitable basis for expanding properties that depend on the alloy configuration. This subset is a non-unique choice as a definition of correlation functions. Non-unique for several reasons; site occupations expressed as 0 or 1 instead of e.g. the Ising definition of +1 and −1; and because in our definition any one of the \(N\) atomic species can be declared redundant. In the following we proceed with the assumption that the Nth species has been declared redundant.[42]

The correlation function expansion of the energy per atom can now be expressed as

$$E[s] = \sum\limits_{\upalpha} {J_{\upalpha} m_{\upalpha} } \left\langle {\upsigma_{\upalpha} [s]} \right\rangle .$$

\(E[s]\) is the energy per atom of the structure \(s\), \(\upalpha\) is short-hand notation for the index of a particular correlation function \(\left\langle {\upsigma_{\upalpha} } \right\rangle = \left\langle {\upsigma_{ij \,\ldots \, k}^{(PQ \, \ldots\, R)} } \right\rangle\), \(J_{\upalpha}\) is the effective cluster interaction (ECI) pertaining to correlation \(\upalpha\) per occurrence, and \(m_{\upalpha}\) is the multiplicity, or the number of clusters \(\upalpha\) per atom. It is to be noted that considering crystal structures with interstitials may benefit from defining multiplicities and structural energies with reference to a lattice point of the disordered structure. However, here we shall avoid such complications and assume we are dealing with simple underlying lattices with just one atom per lattice point in the disordered state as for common fcc- and bcc-based alloys. Often, it is handier to combine \(m_{\upalpha}\) and \(J_{\upalpha}\) into one term, \(\tilde{J}_{\upalpha} = m_{\upalpha} \;J_{\upalpha}\), the ECI per atom.

In the case of a binary AB alloy the probabilities of the pure A clusters only are required for an expansion of E[s]. So for every cluster there is one and only one correlation function. It is now apparent why the actually correct term “correlation function expansion” is usually replaced with the much more common “cluster expansion” as initially binary alloys only were considered.

Expansions based on cluster probabilities can be much more efficient than those based on the Ising convention—even in the case of binary alloys. When the majority type atom is considered as the redundant species, there will be very few clusters consisting of minority atoms only. In fact, in a large simulation cell, say for a Monte Carlo simulation, one can maintain a list of the minority atoms to count quickly how many of those pure minority atom clusters are present. In contrast, using the Ising definition, the particular sign of every instance of a cluster must be evaluated before the value of the corresponding correlation function is known. The more dilute an alloy, the greater the advantage of the current definition.[42]

Inheritance of Expansion Coefficients

Another advantage of the current description is that it is quite trivial to build up an N component CE using, and retaining exactly, the CEs of N − 1 subsystems comprised of N-1 components. In other words, when modeling a ternary alloy ABC one can reuse the ECIs of the AC and BC binaries. The reason for this is that the correlation functions as defined here form an independent basis. In the case of an ABC ternary it is quite simple to rationalize the preservation of ECIs from the AC and BC binaries:

$$\begin{aligned} E[s] = & \sum\limits_{\upalpha} {\tilde{J}_{\upalpha} } \left\langle {\upsigma_{\upalpha} [s]} \right\rangle = \sum\limits_{\upalpha} {\tilde{J}_{\upalpha}^{(AB)} } \left\langle {\upsigma_{\upalpha}^{(AB)} [s]} \right\rangle \\ = \sum\limits_{{\upalpha,n \ne 0}} {\tilde{J}_{\upalpha}^{{(A_{n} B_{0} )}} } \left\langle {\upsigma_{\upalpha}^{{(A_{n} B_{0} )}} [s]} \right\rangle + \sum\limits_{{\upalpha,m \ne 0}} {\tilde{J}_{\upalpha}^{{(A_{0} B_{m} )}} } \left\langle {\upsigma_{\upalpha}^{{(A_{0} B_{m} )}} [s]} \right\rangle + \sum\limits_{{\upalpha,n \ne 0\forall m \ne 0}} {\tilde{J}_{\upalpha}^{{(A_{n} B_{m} )}} } \left\langle {\upsigma_{\upalpha}^{{(A_{n} B_{m} )}} [s]} \right\rangle . \\ \end{aligned}$$

The RHS contains three sums over correlation functions deriving from clusters \(\upalpha\). The 1st of the three sums refers to correlation functions pertaining to AC alloys only because there is no B present. Likewise the 2nd term refers to BC alloys only because there are zero A atoms. The last term only contains correlations that pertain to both A and B atoms. It follows that for a ternary alloy ABC the pure A ECIs can be copied from the AC binary and the pure B ECIs can be copied from the B-C binary provided that the C species is chosen as the redundant species. This can be formulated as: \(\tilde{J}_{{\upalpha A_{n} /AB(C)}} = \tilde{J}_{{\upalpha A_{n} /A(C)}}\) and \(\tilde{J}_{{\upalpha B_{n} /AB(C)}} = \tilde{J}_{{\upalpha B_{n} /B(C)}}\), where the notation \(\upalpha PQ/AB(C)\) refers to the ECI of cluster type \(\upalpha\) (here pair only) with decoration \(PQ\) in the alloy \(ABC\)with the species \(C\) as eliminated species, and where the subscript \(n\) indicates that it is valid for all \(n\)-body pure A and pure B clusters. ECIs from the AB binary are not as trivially preserved exactly. If the CE is limited to pair-wise terms only, i.e. clusters \(\upalpha\) contain two sites at most, it requires a minor algebraic operation only. The \(AB\)pair interactions of the A-B-C ternary can be obtained simply from \(\tilde{J}_{{\upalpha AB/AB(C)}} = \tilde{J}_{{\upalpha AA/A(C)}} + \tilde{J}_{{\upalpha BB/B(C)}} - \tilde{J}_{{\upalpha AA/A(B)}}\). The reason that it is more complicated to derive a similar equation when the CE contains 3-site and larger clusters, is that the 3-site and larger cluster interactions of mixed \(AB\) type all contain energy terms that include all three species simultaneously. Of course, such energy terms cannot originate from a description of any binary. It follows that in the case of pair clusters, and it then does not matter up to which neighbor shell the pairs are considered, all three atomic species cannot be present in one cluster. By induction it then follows that for a quaternary alloy ABCD with D as the eliminated species the ABC ternary ECIs can be exactly preserved provided that the ECIs are limited to clusters of 3 sites or fewer. For a quinary alloy ABCDE all subsystem quaternary CE coefficients can be preserved if no clusters larger than 4-sites are considered. Generally, ECIs pertaining to 4-site clusters are already quite small, and generally it is not necessary to go to 5-site or larger clusters. The implication is that CEs of many-component alloys are completed determined by their subsystems. Another important consequence is that once CEs for all quaternary systems are known, no new CEs need to be performed for quinary or higher component systems because the ECIs are already known from their quaternary subsystems. This is quite a remarkable conclusion given that generally it is believed that determining CEs for many component alloys is impossibly complicated due to the combinatorial explosion of possible combinations of correlation functions that such a CE entails.

It should also be pointed out that the inheritance of ECIs to higher order alloy systems is analogous to the extrapolation methods well-known to CALPHAD practitioners.[43]

To fully take advantage of this inheritance of ECIs from subsystems, it is of course necessary that consistently the same set of underlying clusters is used for all the subsystems. Then a new question arises, one may determine the optimal set of clusters for a CE in some specific binary, but how can one find the optimal set of clusters for a large group of binaries?

Completeness

Another question that arises is how a change of basis, say for re-using the ECIs of the ABCD quaternary in the ABCDE quinary, affects the selection of correlation functions to be used in the CE. This question has been addressed already earlier where it was concluded that a completeness criterion must be met[42]: When a certain cluster is included in the CE all its subclusters must be included as well.[44,45] In multicomponent alloys this completeness criterion must be generalized for a CE to remain invariant under transformation of the occupation variable. For a multicomponent alloy the completeness criterion can be shown to require that if a certain correlation function is included in a CE, (a) all correlations associated with that cluster must be included, and (b) all correlations associated with the subclusters must be included also. The multicomponent completeness criterion can be derived in a completely analogous way as was done for a binary.[42]

Pools of Correlation Functions

In the following sections we will therefore focus on the issue of selecting the optimal set of clusters for a series of binaries. We will limit ourselves to fcc Al-base alloys. The set of cluster will be selected from a certain “pool”. This pool is defined by two criteria: (a) only clusters with up to and including 4 sites are considered, and (b) in such clusters no two sites shall be further apart than the 8th nearest neighbor. We designate this pool as N4R8. The justification of these criteria is as follows: the enthalpy of mixing is generally represented as a polynomial in the composition. The highest power in this polynomial is an indication of the number of sites in the largest cluster that significantly contributes to the alloy energy. E.g. a parabolic enthalpy of mixing, symmetric around equiatomic composition, indicates that only 2 body (i.e. pairwise) interactions are needed and three- four- and larger body interaction terms can be neglected. Extensive experience in fitting binary phase diagrams has shown that usually a sub-regular (i.e. a third order polynomial) or more rarely, a fourth order polynomial in the composition is completely adequate to represent the enthalpy of mixing accurately. Therefore, ECIs with 4 sites (N4) should generally be adequate. With the exception of long-period superstructures, such as in Cu-Pd, all experimentally observed fcc superstructures can be stabilized by pairwise interactions with ranges up to the 8th nearest neighbor (R8). The experimentally observed Al3Zr phase (StrukturBericht notation:D022) is stabilized by the 8th nearest neighbor (2 0 0 afcc, see Fig. 1). The N4R8 pool contains 1 point cluster, 8 pair clusters, 50 three body, and 427 four body clusters for a total of 486 clusters. In addition we must count the so-called empty cluster with zero sites. The “cluster interaction” corresponding to the empty cluster represents a constant off-set in the energy. Including this empty cluster there are 487 clusters in the N4R8 pool.

Figure 1
figure 1

The 8 neighbor pairs included in the N4R8 cluster pool.

Full size image

The versatility of the N4R8 set of clusters is nicely illustrated by the accurate representation of the GP morphology. A particularly challenging issue for any CE without explicit treatment for long-ranged elastic interactions is the prediction of GP zone shapes.[46] In Al-Cu with about 2 a/o Cu, GP zones are known to form as pure Cu on {100} planes separated by 2 or 3 atomic planes of pure Al. Initially, it is believed that there are 3 intermediary Al planes, but absorption of vacancies and concomitant relaxation rapidly reduces this to 2 atomic Al layers.[47–49] Describing the Cu-Al-Al-Al sandwich morphology requires a highly optimized CE with a LOOCV of just 1 meV/atom, with about 200 fitted structural energies and 80 ECIs. see Fig. 2.

Figure 2
figure 2

(left) Distance to the convex hull as function of the Cu atomic concentration in Al-rich Al-Cu alloys according to ab initio calculations and as obtained with a N4R8 CE using 80 ECIs and about 200 structural energies representing the whole Al-Cu composition range. The stability of the transitory GP zones consisting of single Cu (100) planes separated by 3 Al planes is readily apparent at X(Cu) = 0.25. At right only Cu atoms are displayed in a box formed by 20 × 20 × 20 fcc cubes with 2 a/o Cu. In the kinetic Monte Carlo simulation using the CE the early stages of precipitation are simulated at 300 K. A GP zone can be recognized in the lower RHS of the box.

Full size image

On the Impossibility of Finding the Best Expansion

Finding the best CE for a certain alloy, using a large set of structural energies, and using a pool of clusters with \(N\) members is a daunting task. The total number of combinations \(P(N)\) that can be generated by selecting arbitrarily a set of clusters with anywhere from 1 to \(N\) members can be calculated as follows:

$$P(N) = \frac{N!}{(N - 1)!(1)!} + \frac{N!}{(N - 2)!(2)!} + \cdots + \frac{N!}{(N - N)!(N)!} = \sum\limits_{i = 1}^{N} {\left( {\begin{array}{*{20}c} N \\ i \\ \end{array} } \right)} = 2^{N} - 1.$$

The value of \(P(N)\) is easily understood because each cluster either is included, or is not included, which gives \(2^{N}\), but we explicitly excluded the possibility of a completely empty combination so that one has to be subtracted. When \(N = 487\) the value of \(P\) is approximately \(4 \times 10^{146}\), and this is considering a single binary only! It is not feasible to evaluate all possible CEs and select the best performing one exactly. One has to settle for a “good” CE, rather than expect to find the “best” CE. How well a CE performs can be judged with some fitness criterion. Common fitness criteria are (a) the root mean square fitting error for the known structural energies, sometimes modified by other criteria such as whether or not correct ground states are produced by the CE[50]; (b) a measure of “predictive ability” of a CE,[14,50,51] such as the leave-one-out cross-validation score[44] or leave-many-out cross-validation score.[3]

Several methods for finding “good” CE have been proposed. Various statistical methodologies have been discussed in e.g. Ref 52,44,53, and 54. Here we mention 4 methods. (I) “aufbau” where a given CE is expanded with a single new cluster, one at a time.[55] All not yet included clusters are considered. Among the set of not yet included clusters the one that gives the best improvement in the fitness criterion is selected. Now, a new CE has been generated and the process is repeated. Repetitions stop either when the maximal number of clusters in the CE is reached, or when the fitness criterion improves too little, or deteriorates. (II) Singular value decomposition.[56] When there are not precisely \(N\) structural energies available, the \(\left\langle {\upsigma_{\upalpha} [s]} \right\rangle\) matrix is not square and only a pseudo-inverse can be defined. Usually, the number of structural energies is less than \(N\), so that there is an under-determined set of equations to be solved. Oftentimes the \(\left\langle {\upsigma_{\upalpha} [s]} \right\rangle\) matrix is ill-conditioned for various reasons which to some extent can be mitigated by adding very small random numbers. Generally, this methods works best when the set of equations is over-determined, i.e. when the number of structural energies is larger than \(N\). This is in practice rarely the case. When this method succeeds in generating a CE it is optimal in the sense that it produces a small fitting error. The SVD method can be modified in order to better utilize insight in underlying physical properties, see Ref 57. (III) Genetic algorithm.[11] A population of distinct CEs is allowed to ‘mate’ (i.e. exchange expansion terms) and the resulting offspring is then culled on the basis of the fitness criterion. This procedure of is repeated for a number of generations, till the fitness criterion no longer improves. (IV) Enumeration in combination with completeness and mandatory clusters.[55] Imposition of the completeness criterion drastically reduces the number of acceptable CEs. If furthermore it is imposed that certain clusters, such as the empty cluster, the single point and nearest neighbor pair clusters are always required in a valid CE the number of CEs can be reduced further. A complete CE is fully characterized by its maximal clusters only. When only CEs are considered with a limited number of maximal clusters their total number remains relatively small. In the case of binary fcc alloys with the N4R8 cluster pool and imposition of completeness and mandatory inclusion of the empty, point, nearest and next nearest pair clusters, and considering only CEs with 4 or fewer maximal clusters, there remain just 2 018 401 138\(( \approx 2 \times 10^{9} )\) CEs only. While this number is still very large, it can be evaluated in a number of weeks to months on a single CPU core. This 4th method is used below.

It should be remarked that enumeration with a limited number of maximal clusters biases CEs with completeness towards the clusters with larger numbers of sites. Larger clusters are favored because they contain several subclusters and thus yield a greater improvement in the “fitting criterion” than smaller clusters. With a handicap or weighting function this bias can be ameliorated to some extent.

To illustrate that a single set of clusters can yield acceptable CEs across a range of alloys, we considered all major alloying elements in Al-base alloys. Leave-one-out cross-validation scores (LOOCV) have been determined for CEs of 9 binary Al alloys, Al-Cu, Al-Fe, Al-Li, Al-Mg, Al-Mn, Al-Si, Al-Ti, Al-Zn, Al-Zr. The CEs are complete as discussed in section 2.3. The CEs are based on the N4R8 pool with up to 4 maximal clusters. For each binary a set of 100 ab initio computed structural energies was used for fitting. Enumeration gave 2 018 401 138 CEs for each binary. To find the optimal CE across all 9 binaries we computed the product of all 9 LOOCVs for a given set of maximal clusters. The resulting set of clusters is shown in Fig. 3.

Figure 3
figure 3

The 4 maximal clusters (white spheres) that minimize the product of LOOCVs of 9 binary Al alloys. Fcc cubes and dashed lines have been added for clarity.

Full size image

Including the empty cluster, the maximal clusters shown in Fig. 3 have 20 subclusters, thus there are 24 ECIs in our optimal CE for Al-alloys, Al-optimal for brevity. For a ternary alloys the number of ECIs in Al-optimal is 146 out of the more than 7000 that occur within the N4R8 pool for ternaries. Al-optimal gives small LOOCV values for binaries (Al-Mg: 1.3 meV/atom, Al-Si: 2.8 meV/atom) by design, but for the Al-Mg-Si ternary also, the LOOCV has a small value of just 2.2 meV/atom. Of course, as mentioned in section 2.2 the interactions of the Al-Mg and Al-Si binaries were inherited in describing the ternary. It should be remarked that with 100 structural energies per binary, while extracting only 24 ECIs, the CE is very overdetermined and as a consequence the LOOCV takes values that are very close to the root of the mean square error of the fit. In addition to using 100 structural energies for each of the three constituent binaries, an additional 100 structural energies pertaining to truly ternary compounds were used. The Al-Mg-Si CE was used to predict plausible initial coherent, i.e. fcc-based, stages of precipitation and resulting structures are displayed in Fig. 4.

Figure 4
figure 4

Fcc-based superstructures predicted by the Al-optimal CE for Al-Mg-Si: (a) Al4Mg3Si, (b) Al8Mg2Si2, (c) Al6Mg2Si2, (d) Al2MgSi, (e) Al4Mg2Si2. Al: light grey spheres, Mg: dark grey spheres marked with X, and Si: black encircled spheres.

Full size image

Cluster Expansions for Vacancy-Mediated Diffusion in Substitutional Alloys

When vacancies trade places with neighboring atoms in an alloy, a certain activation barrier must be overcome, see Fig. 5. When the vacancy is considered as an additional atomic species, it is apparent that the energies of state 1 (\(E_{1}\)) and state 2 (\(E_{2}\)) can be described by a multinary CE. However, for the activated state between states 1 and 2 problems arise. In the activated state the atom that trades places with the vacancy is no longer uniquely associated with a single lattice site. This is a problem because the cluster expansion is built upon the concept of there being a lattice gas where every site is associated with one, and only one, atomic species. A second problem is that the energy barrier is not purely a “state function” because the height of the barrier depends on the direction of the swap, the transition \(1 \to 2\) has a different barrier than transition \(1 \leftarrow 2\). This last problem is elegantly solved by van der Ven et al. by defining the kinetically resolved activation barrier,[21] defined as

$$E_{KRA} = E_{tr} - \frac{1}{2}\left( {E_{1} + E_{2} } \right),$$

where \(E_{tr}\) is the highest energy along the lowest energy path connecting the states 1 and 2. When \(E_{KRA}\), \(E_{1}\) and \(E_{2}\) are known it is trivial to extract the energy barriers for transitions \(1 \to 2\) and \(1 \leftarrow 2\).

Figure 5
figure 5

Schematic view of vacancy-mediated diffusion of a substitutional atom. E 1 (E 2) is the energy in state 1(2), E tr is the energy is the transition state. For movement from state 1 to 2 (2 to 1) an energy barrier E tr − E 1 (E tr − E 2) must be overcome.

Full size image

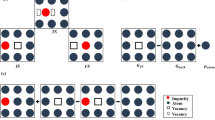
The first problem, the lattice gas violation, can also be resolved by introducing a new atomic species for the vacancy-swapping atom pair, “swapping pair” for brevity, as displayed in Fig. 6. When a single vacancy is present only in an N-component alloy (here N = 3: black species, donut species, and vacancy), replacing the swapping pair by two “atoms” of a new atomic species, results in N − 1 new N component systems. Thus the complexity of the problem is not significantly increased. When the value of \(E_{KRA}\) is computed in actual alloys, it is found to vary strongly with atomic occupancy right around the swapping pair. In Al-Cu alloys the largest and smallest values might easily differ by a factor 3. To illustrate the significant local neighborhood dependence of the KRA energies, some Al-Cu supercells are shown with the corresponding values of \(E_{KRA}\) in Fig. 7.

Figure 6
figure 6

Transition states (left side) in a binary alloy with vacancies are mapped onto a lattice gas featuring two distinct ternaries (top: black, donut, and a black jumping atom represented as a black donut swapping pair; bottom: black, donut and a donut jumping atom represented as a filled donut swapping pair).

Full size image
Figure 7
figure 7

Supercells with transition states. Dark (light) grey spheres: Cu (Al), large grey sphere: Al in a transition state, small black bordered spheres: half vacancy. The kinetically resolved activation barrier is (a) 0.22 eV in Al23Cu8Vac and (b) 0.65 eV in Al31Vac.

Full size image

As \(E_{KRA}\) is a strong function of the local environment, a local CE appears a sensible approach. A local CE should depend only on atomic occupancy right near the swapping pair and this expansion should not describe the average energetics of the alloy, which is already covered in the CE for states 1 and 2. This is easily achieved by selecting only correlation functions that encompass the swapping pair. We emphasize that the whole pair should be included because otherwise correlation functions may not be properly distinguished, as illustrated in Fig. 8. The reason for this is that the introduction of the swapping pair has eliminated many operations from the symmetry group of the underlying disordered crystal structure. Only operations that preserve the swapping pair can be retained. As the local CE retains only correlations that contain the swapping pair, it is apparent that such a local CE is NOT complete in a strict sense, because subclusters that contain only one or no sites of the swapping pair are excluded. Of course, one can retain the completeness property with regard to the local environment of the swapping pair. The local CE can be expressed as

$$E_{KRA} = \sum\limits_{\upalpha} {\sigma_{{\upalpha \cup\upbeta}} } \;J_{{\upalpha \cup\upbeta}} ,$$

where \(\upalpha\) represents a cluster decoration corresponding to the empty cluster, or a point cluster, etc. but not part of the swapping pair, \(\upbeta\) represents the swapping pair, \(\upsigma_{{\upalpha \cup\upbeta}}\) is a counter for the number of cluster decorations of type \(\upalpha \cup\upbeta\), and \(J\) is the corresponding ECI. \(\upsigma_{{\upalpha \cup\upbeta}}\) has a maximum value \(\upmu_{{\upalpha \cup\upbeta}}\) that is determined by its symmetry, e.g. for the decorations encircled by the oval in Fig. 8 it is 4 (left side) and 2 (right side).

Figure 8
figure 8

Black filled donuts indicate the swapping pair on a (100) plane in fcc. In the local CE, the nearest neighbor pair (indicated by the grey line) on the left and the pair on the right are not equivalent but are not properly distinguished when applying the symmetry of the underlying lattice gas. However, when the swapping pair is completely included, as in the clusters enclosed by the dashed lines, the inequivalence is readily apparent.

Full size image

Positive Definite Local Cluster Expansions

Another aspect of the \(E_{KRA}\) local CE is that it should generally yield positive values for all local neighborhoods. Unlike configurational energies which can be both positive and negative, here only positive energies are desired. In the local CE occurrences of cluster decorations are counted. As these occurrences can be counted using positive numbers only, it is tempting to assume that a strictly positive expansion can be obtained by requiring all ECI non-negative. However, this is a severe restriction that makes it generally too difficult to obtain a good CE. A less severe restriction can be designed. The interaction J β for the empty cluster should be positive. The sum of all negative valued interactions, times their maximal multipliers \(\upmu_{{\upalpha \cup\upbeta}}\), plus the \(J_{\upbeta}\) should thus be positive, \(J_{\upbeta} + \frac{1}{2}\sum\limits_{{\upalpha* \, }} {\mu_{{\upalpha \cup\upbeta}} } \left( {J_{{\upalpha \cup\upbeta}} - \left| {J_{{\upalpha \cup\upbeta}} } \right|} \right) > 0\), where \(\upalpha*\) in the sum indicates that the empty cluster is excluded. This less restrictive condition is easily implemented in the aufbau and enumeration methods. The most effective method we have found however, is another method; Immediately screening every CE for a large number of pre-selected local environments and requiring that for all these test environments the \(E_{KRA}\) exceeds zero or some small positive value.

Conclusion

It has been shown that the definition of the correlation functions is a crucial aspect of cluster expansions. Particularly for multicomponent alloys, the current definition of the correlation functions allows inheritance, i.e. effective cluster interactions from constituent systems can be directly re-used. This assures that a good description of the alloy energetics in constituent systems is carried forth in more complex alloys. It also great facilitates determining cluster expansions in alloys with many components because it was shown that if N-body terms in a CE suffice for describing the energetics of an alloy, then alloys with N + 1 components do not require any interactions beyond those present in the N + 1 constituent systems with N components. As generally CEs with 4-body terms are capable of describing alloy energetics to within the meV/atom range, it follows that quinary alloys already, can be fully described using the energetics of the constituent quaternaries only. This observation is also an indication why there are so very few multicomponent superstructures in metallic alloys. Another aspect of the current formulation of correlation coefficients is the great efficiency in evaluating the energy in dilute binaries and multicomponent alloys generally. Efficient algorithms for determining CEs were presented. These methods were illustrated by determining a set of clusters that yields good CEs for multiple Al-based alloys. Finally, the peculiarities of strictly local CEs, e.g. for KRA energy barriers for vacancy mediated diffusion in substitutional alloys, were discussed. A method to impose that such local CEs yield only positive energy barriers was presented.