Introduction

The sedimentation process, i.e. gravity induced diffusion, is generally known as the transport phenomena of macroscopic solutes induced by gravitational or centrifugal field.[1] The sedimentation of isotope atoms in liquids is important from the point of view of separation of isotopes.[2] Enriched isotopes are crucial in the fields of atomic energy 235U, 6Li, etc.[3] medical treatment 50Cr, 168Yb, etc.[4] and in the information technology field for quantum computing 29Si, etc.[5] In the 1970s, Barr and Smith and Anthony[6,7] investigated the sedimentation of Au atoms in elemental metals (K, In and Pb) with low melting temperatures under maximum acceleration fields of 1-2 × 105 g. In 1996, Mashimo et al. developed an ultracentrifuge apparatus that can generate an acceleration field up to 106 g for long times at high temperatures.[8] The second-generation ultracentrifuge was newly developed, in 2001.[9] Using this apparatus he studied the sedimentation the substitutional solute atoms in different elements[10–12] e.g. ultracentrifuge experiments at high temperature on elemental selenium to examine the sedimentation of isotope atoms in liquid matter.[2]

Almost all sedimentation processes are described by the Lamm equation proposed in 1929.[13] This classical equation was formulated for axially symmetric macroscopic particles on the basis of macroscopic mechanics and thermodynamics. The fundamental idea of Lamm is that the driving force between the centrifugal field acting on the macro solute is given by the difference between the centrifugal force and the buoyant force caused by the surrounding liquid solvent.[1] Several approaches to the Lamm equation were made. Brenner and Condiff extended method for particles of arbitrary shape and considered the rotation effect.[14] However in these approaches the self-interaction effects among macroscopic solutes caused by the centrifugal field are not considered, therefore, the driving force is not expressed as a function of solute concentration, i.e. the density of the mixture solvent does not change with concentration.[1]

In 1988 Mashimo proposed an equation for describing the diffusion of atoms induced by the centrifugal field in a two component system.[1] His theory is based on linear irreversible thermodynamics (Onsager relations) and the Nernst-Einstein relation considering the effect of concentration change.[1] The Mashimo’s theory considers the chemical activity of the simulated system by introducing the Q parameter (the ratios of the diffusion coefficient matrix). The disadvantage of the Mashimo theory is the assumption of the unknown diffusivity under the combined stress and gravity forces.

In the previous paper the bi-velocity method, the rigorous mathematical derivation of the mass, momentum and energy conservations laws and the results of the method for binary Bi-Sb diffusion couple were presented.[15] In this work the model is applied to simulate the multicomponent sedimentation process when the ideality sweeping statement is applied (i.e. chemical activity is equal to the concentration). Using the bi-velocity method for the first time the application of the formalism in modeling the ternary interdiffusion of selenium isotopes is shown.

Mashimo et al.[16,17] Sedimentation Model

Mashimo model based on the Onsager flux expression, has the form:

$$ J_{i} = - \sum\limits_{l} {\left( {D_{il}^{1} \frac{{\partial c_{l} }}{\partial x}} \right)} + \sum\limits_{j} {\left( {\frac{{D_{ij}^{2} }}{RT}g\left( {M_{j} - M_{j}^{*} } \right)} \right)c_{i} } ,\quad i = 1,2, \ldots ,r $$
(1)

where J i , c i and M i denote the overall flux (diffusion and convection), the concentration and atomic mass of ith component, respectively. \( M_{j}^{*} \) is the effective mass of the surrounding solvent mixture per molar volume. R, T and g denotes the gas constant, temperature and gravity force, respectively. \( D_{il}^{1} \) denotes the intrinsic diffusion coefficient, \( D_{ij}^{2} \) is the unknown (experimentally determined) sedimentation coefficient under the gravity force.

The effective mass of the surrounding solvent mixture per molar volume is expressed by the weighted average:

$$ M_{j}^{*} = {{\left( {\sum\nolimits_{l} {\frac{{\Upomega_{j} }}{{\Upomega_{l} }}c_{l} M_{l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{l} {\frac{{\Upomega_{j} }}{{\Upomega_{l} }}c_{l} M_{l} } } \right)} {\left( {\sum\nolimits_{l} {c_{l} } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sum\nolimits_{l} {c_{l} } } \right)}},\quad j = 1,2, \ldots ,r $$
(2)

where \( \Upomega_{j} \) denote the partial molar volume of the jth component.

The diffusion coefficients are expressed by the phenomenological transport coefficients, L ij , and chemical potential, μ ch j :[16]

$$ D_{il}^{1} = \sum\nolimits_{l} {\left( {L_{ij} \frac{{\partial \mu_{j}^{\text{ch}} }}{{\partial c_{l} }}} \right)} ,\quad D_{ij}^{2} = L_{ij} \frac{kT}{{c_{i} }},\quad i,j = 1,2, \ldots ,r $$
(3)

Consequently, using the flux equation Eq 1, Mashimo derived the conservation law in the form of the second Fick’s law:

$$ \frac{{\partial c_{i} }}{\partial t} = \frac{\partial }{\partial x}\left( { - \sum\limits_{l} {\left( {D_{il}^{1} \frac{{\partial c_{l} }}{\partial x}} \right)} + \sum\limits_{j} {\left( {\frac{{D_{ij}^{2} }}{RT}g\left( {M_{j} - M_{j}^{*} } \right)} \right)} } c_{i} \right),\quad i = 1, \ldots ,r $$
(4)

It is worth noticing, that in such description of the sedimentation process, the drift (convection) velocity is expressed by:

$$ \upsilon^{\text{drift}} = \sum\nolimits_{j} {\left( {\frac{{D_{ij}^{2} }}{RT}g\left( {M_{j} - M_{j}^{*} } \right)} \right)} . $$
(5)

The presented model was used by Mashimo to simulate the sedimentation of binary systems, mainly the Bi-Sb, Se-Te and In-Pb. In the next section the mathematical model describing the gravity induced sedimentation process in multicomponent system is presented.

The Conservation of Momentum and Volume Continuity (Bi-velocity Method)

The overall velocity of the ith component, υ i , is a sum of diffusion, Darken (convection) and deformation velocities, respectively:

$$ \upsilon_{i} = \upsilon_{i}^{d} + \upsilon^{\text{drift}} = \upsilon_{i}^{d} + \upsilon^{D} + \upsilon^{\sigma } $$
(6)

The component diffusion flux, should be expressed by the proper constitutive formula. In this work the Nernst-Planck flux equation[18,19] is used:

$$ J_{i}^{d} \equiv \rho_{i} \upsilon_{i}^{d} = \rho_{i} B_{i} F_{i}^{{}} , $$
(7)

where B i and F i denote the mobility and the forces acting on the ith component, respectively;

$$ F_{i}^{{}} = - {\kern 1pt} {\text{grad}}{\kern 1pt} \left( {\mu_{i}^{ch} + \mu_{i}^{m} } \right) + F_{i}^{\text{centr}} = - {\kern 1pt} {\text{grad}}{\kern 1pt} \mu_{i}^{{}} + F_{i}^{\text{centr}} $$
(8)

where μ i is the diffusion potential;μ ch i and μ m i denote the chemical and mechanical potentials. F centr i is the centrifugal force acting on the ith component (\( F_{i}^{\text{centr}} \) = M i g, where M i is the molar mass of the ith component and g is gravitation force).

The mechanical potential in case of sedimentation processes is expressed as:

$$ \mu_{i}^{m} = \Upomega_{i}^{m} p^{g} $$
(9)

where \( \Upomega_{i}^{m} \) denote the partial mass volume of the ith component and p g is a pressure, Eq 9.

By Newton’s law the rate of momentum change equals the overall force acting on the mass in \( \left| {\Upomega \left( t \right)} \right| \):

$$ \frac{d}{dt}\int\limits_{{\left| {\Upomega \left( t \right)} \right|}} {\rho \upsilon^{m} dx } = F^{\text{total}} = \sum\limits_{i} {F_{i}^{\text{total}} } = \sum\limits_{i} {\frac{d}{dt}\int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\rho_{i} \upsilon_{i} dx} }\,=\,\sum\limits_{i} {\left( {F_{i}^{\sigma } + F_{i}^{\text{ext}} } \right)} . $$
(10)

where the force of elastic stress, \( F_{i}^{\sigma } \) is defined:

$$ F_{i}^{\sigma } = \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\text{div} \left( {\Upomega_{i}^{m} \rho_{i} {\varvec{\sigma}}} \right)dx} , $$
(11)

where \( {\varvec{\sigma}} \) denotes Cauchy stress tensor.

In case of the sedimentation process the external force F ext is induced by the buoyant force, thus:

$$ F_{i}^{ext} = F_{i}^{g} = \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\rho_{i} r\omega^{2} dx} . $$
(12)

Applying the formulae (10)-(12) results in the i-component momentum change in a subregion \( \left| {\Upomega_{i} \left( t \right)} \right| \):

$$ \frac{d}{dt}\int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\rho_{i} \upsilon_{i} dx} = \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {{\text{div}}\left( {\rho_{i} \Upomega_{i}^{m} {\varvec{\sigma}}} \right)dx} + \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\rho_{i} r\omega^{2} dx} $$
(13)

Using the Liouville theorem the left hand side of Eq 13 becomes:

$$ \frac{d }{dt}\int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\rho_{i} \upsilon_{i} dx} = \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\left( {\upsilon_{i} \left( {\frac{{\partial \rho_{i} }}{\partial t} + {\text{div}}\left( {\rho_{i} \upsilon_{i} } \right)} \right) + \rho_{i} \left( {\frac{{\partial \upsilon_{i} }}{\partial t} + \upsilon_{i} \cdot \text{grad} \,\upsilon_{i} } \right)} \right)dx} = \int\limits_{{\left| {\Upomega_{i} \left( t \right)} \right|}} {\left. {\rho_{i} \frac{{{\text{D}}\upsilon_{i} }}{{{\text{D}}t}}} \right|_{{\upsilon_{i} }} dx} . $$
(14)

From the arbitrariness of the subregion \( \left| {\Upomega_{i} (t)} \right| \) Eq 13 becomes:

$$ \left. {\rho_{i} \frac{{{\text{D}}\upsilon_{i} }}{{{\text{D}}t}}} \right|_{{\upsilon_{i} }} = {\text{div}}\left( {\rho_{i} \Upomega_{i}^{m} {\varvec{\sigma}}} \right) + \rho_{i} r\omega^{2} \quad {\text{for}}\quad i = 1, \ldots ,r. . $$
(15)

By summing Eq 15 for all components the overall equation of motion in all media in which diffusion is non-negligible is:

$$ \sum\limits_{i} {\rho_{i} \left. {\frac{{{\text{D}}\upsilon_{i} }}{{{\text{D}}t}}} \right|}_{{\upsilon_{i} }} = {\text{div}}{\varvec{\sigma}} + \rho r\omega^{2} . $$
(16)

where r is a radius and ω the angular speed.

To calculate the stationary sedimentation process the mechanical equilibrium should be assumed, thus the above equation of motion is reduced to the following form:

$$ 0 = {\text{div}}\,{\varvec{\sigma}} + \rho r\omega^{2} . $$
(17)

Volume Continuity Eq 15

In linear irreversible thermodynamics the partial molar volumes are intensive parameters and are not conserved. The volume, \( \left| {\Upomega \left( t \right)} \right| \) occupied by the mixture at the moment t, \( \left| {\Upomega \left( t \right)} \right| = \int_{\Upomega \left( t \right)} {dx} \), is affected by the distribution of every mixture component and stress field. In this paper the limiting situation, when the volume changes due to the external stress field only (gravity), is analyzed, thus:

$$ \int\limits_{{\left| {\Upomega \left( t \right)} \right|}} {{\text{div}}\left( {\rho \Upomega^{m} \upsilon } \right)dx} = \int\limits_{{\left| {\Upomega \left( t \right)} \right|}} {{\text{div}}\upsilon^{\sigma } dx} . $$
(18)

Integrals can be omitted and differential form of the VCE follows:

$$ {\text{div}}\left( {\rho \Upomega^{m} \upsilon } \right) = {\text{div}}\upsilon^{\sigma } , $$
(19)

Cauchy Stress Tensor

A common approach when defining the relation between pressure and energy of the stress field in solids is to neglect the torsion.[20] Here, in order to consider the overall stress energy, Schur decomposition[21] is used. Such transformation allow to diagonalize the symmetric stress tensor. The pressure (generated by the external force) is defined than as the trace of the diagonal stress tensor (diagonalized Cauchy stress tensor, \( {\varvec{\sigma}} \)),[22]

$$ p^{g} = - \frac{1}{3}{\text{tr}}({\varvec{\sigma}}^{*} ) = - \frac{1}{3}{\varvec{\sigma}}^{*} :{\mathbf{I}} = - \frac{1}{3}\left( {\lambda_{1} + \lambda_{2} + \lambda_{3} } \right), $$
(20)

where \( \lambda_{i} \) are the eigenvalues of Cauchy stress tensor.

Finally the stress tensor will be defined from the definition of the pressure,

$$ {\varvec{\sigma}} = - p^{g} {\mathbf{I}} \Rightarrow {\text{div}}{\varvec{\sigma}} = - \text{div} \left( {p^{g} {\mathbf{I}}} \right) = - \text{grad} \,p^{g} . $$
(21)

The momentum conservation law, Eq 17, has now the form

$$ \text{grad} \,p^{g} = \rho r\omega^{2} , $$
(22)

where the stress tensor and pressure are related by Eq 20 and 21.

Initial Conditions

The initial density distribution of the ith component: \( \mathop \rho \limits^{0}_{i} \).

Boundary Conditions

The diffusion flux of the ith component at the mixture boundary, \( \rho_{i} \upsilon_{i}^{d} \left( t \right) \cdot n = 0\quad {\text{on}}\quad \partial \left| \Upomega \right| \), where n represents the unit vector normal to the boundary i.e., in the closed system analyzed here, the mass flow through the mixture boundaries does not occur.

Numerical Solution

The solution of the presented model was obtained in several steps: (1) discretization of the problem (mathematical reformulation), (2) numerical solution using Finite Difference Method (FDM), (3) solving the resulting system of ordinary differential equations and computer implementation of method. The differential equations solver based on the Runge-Kutta-Fehlberg method with adaptive stepsize control. Fehlberg discovered a fifth-order method with six function evaluations where another combination of this six functions gives a fourth-order method. The difference between these two estimates can then be used as an estimate of the truncation error to adjust the stepsize.[23]

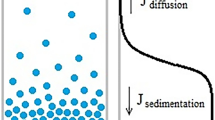
The schematic presentation of the two dimensional model is shown on Fig. 1. The simulations consider the diffusion flux along the gravity direction. The dotted line represent the one-dimensional mapping of the simulated results. The forces acting on the surface of the sample in X, Y Cartesian coordinate system are defined as:

$$ \begin{aligned} F_{x} & = \omega x, \\ F_{y} & = 0. \\ \end{aligned} $$

Using such representation the equations describing the forces in the rotated system (X′Y′) are:

$$ \begin{aligned} F_{{x^{\prime}}} & = \omega^{2} \left( {(\ell + y^{\prime } )\sin \alpha + x^{\prime } \cos \alpha } \right)\cos \alpha , \\ F_{{y^{\prime}}} & = \omega^{2} \left( {(\ell + y^{\prime } )\sin \alpha + x^{\prime } \cos \alpha } \right)\sin \alpha . \\ \end{aligned} $$
Fig. 1
figure 1

The schematic presentation of the 2 dimensional sedimentation model

Full size image

Results

As an example the sedimentation process in the Se-Te binary system[24] is presented. The results of the simulations are compared with the Mashimo et al. experiments and his calculations. The data used to calculate the sedimentation process in Se-Te system are presented in Table 1. The presented simulation results were calculated using the steady state approximation, i.e. the simulations were performed until no change of the concentration profile was observed.

Table 1 The data used to simulate the sedimentation process in Se-Te binary systems
Full size table

To calculate the sedimentation the two dimensional model was used. The results are shown in Fig. 2. The dots shows the experimental values of the sedimentation process, the dashed line present the simulations from the Mashimo et al.[24] model and the solid line model presented in this work.

Fig. 2
figure 2

The sedimentation process in Se-Te system

Full size image

The next example shows the sedimentation of Selenium isotopes. The calculated composition ratio of 82Se/76Se is compared with the experimental results.[25] The simulations were performed in three-components system. The two components were the isotopes and the third was the reference ideal component. The data used in calculations is shown in Table 2.

Table 2 The data used to simulate the sedimentation process for composition ratio of 82Se/76Se
Full size table

The results of the composition ratio of 82Se/76Se compared with the (a) experimental results and (b) Mashimo model[2] are shown in Fig. 3.

Fig. 3
figure 3

The sedimentation process of Selenium isotopes. The composition ratio of 82Se/76Se (line) compared with the experimental results (dots)

Full size image

The last example, Fig. 4, present the sedimentation in three-component system InGeSb, the Te-free recording material for high speed recording application.[26] The data used in simulations is shown in Table 3.

Fig. 4
figure 4

The sedimentation in three-component system In-Ge-Sb

Full size image
Table 3 The data used to simulate the sedimentation process of InGeSb ternary system
Full size table

Conclusions

In this paper a mathematical model describing the gravity induced sedimentation process in multicomponent system is presented. The model is based on the generalized interdiffusion method (bi-velocity method): (1) the volume continuity equation, (2) equation of motion, (3) Cauchy stress tensor and (4) Nernst Planck flux formulae. In the present approach the plastic deformation is neglected. The method was applied to simulate the sedimentation processes of the selenium isotopes and the ternary InSbGe system.

The model can be extended by introducing the elastic stress field induced by the diffusion process. Consequently, the pressure field will consist two parts: (1) the pressure generated by the external field (gravity), p g and (2) pressure generated by the differences in composition (chemical forces), p d. The p d can be calculated from overall dilatation of the system:[27]

$$ \frac{{\partial p^{d} }}{\partial t}{ = } - \frac{E}{{3\left( {1 - 2v} \right)}}{\text{div}}\upsilon^{d} $$

where: E denote the Young modulus and v Poisson number. In such a case the diffusion velocity can be rewritten as:

$$ \upsilon_{i}^{d} = - B_{i} \,{\text{grad}}\left( {\mu_{i}^{ch} + \Upomega_{i} p^{g} + \Upomega_{i} p^{d} } \right) + B_{i} M_{i} r\omega^{2} . $$