Bending of a Bimetallic Beam Due to the Kirkendall Effect

Abstract

The time-dependent bending of single-phase and two-phase bimetal strips due to interdiffusion is computed. The model couples simple beam theory and diffusion with bending due to the creation and/or annihilation of vacancies necessitated by unequal lattice diffusion rates of the two metals. The single-phase analysis employs a Fourier method for the diffusion analysis and predicts a beam curvature that is initially proportional to time and later reaches a constant value. The two-phase analysis, which involves a moving interphase boundary, employs an error function solution for the diffusion problem to model early times and a numerical solution for later time. Unlike the single-phase results, linear behavior is obtained at early time only if the original interface is centered in the beam. In general, the curvature initially is proportional to the square root of time. The numerical solution gives the gradual transition of the curvature to a constant value at late time. In some cases, nonmonotonic time dependence is obtained for the curvature for the two-phase beam.

Introduction

The Kirkendall effect due to unequal diffusion rates of atomic species is well known to cause the formation of voids. The voids form in response to the condensation of excess vacancies when insufficient vacancy sinks (grain boundaries and climbing dislocations) are available. With sufficient vacancy sources and sinks, lattices sites are destroyed and different parts of the lattice are displaced with respect to each other (Kirkendall shift). Less well known is the bending of thin samples subject to transverse diffusion due to the Kirkendall effect.

Experiments and models elucidating bending have been executed for solid solution alloys of Au–Ag by Stevens and Powell,[1] of Cu-Ni by Daruka et al.,[2] and of Zr-Ti by Opposis et al.[3] Suo et al.[4] describes a practical application of this subject where the stresses and bending due to the difference of diffusion rates of oxygen and metals in thermal barrier coatings have been investigated. A beam that undergoes transverse diffusion may also bend if the lattice parameter (or alternately, the molar volume) depends on mole fraction even if the intrinsic diffusion coefficients are equal. The rigorous basis for these effects was described by Stephenson,[5] who also described the transition between the limiting cases of the “Darken” and “Nernst-Plank” limits of coupled diffusion and deformation as various parameters vary according to the material of interest.

Daruka et al.[2] performed numerical, analytical, and experimental investigations of the bending of single-phase plates undergoing diffusion with unequal diffusion rates for two species. Their experiments clamped an entire edge of a plate and thus their analysis focused on the cylindrical geometry and required an analysis of the clamping moment. An analytical result from their work relates the curvature of the cylindrical plate,$\upkappa$, to time as

$$ \upkappa (t) = 6\,{\frac{{\left[ {\bar{D}_{\text{B}} - \bar{D}_{\text{A}} } \right]}}{{\updelta^{3} }}}\,t, $$

(1)

where $\updelta$ is the beam thickness and the $\bar{D}_{\text{i}}$ are concentration-weighted average intrinsic diffusion coefficients.¹ This expression was derived from their general model for times when the diffusion distance is much less than the beam thickness and in the limit of high creep rate when the viscosity $\upeta$ of their Maxwell solid tends to zero. In their general model, which is numerically evaluated, they allow for a dependence of diffusion flux not only on gradients of concentration but also on gradients of pressure. This coupling allows them, like Stephenson,[5] to recover Darken and Nernst-Plank limits of diffusion/viscous flow behavior.

A simpler model is presented herein because the direct effect of pressure gradient on diffusion flux is neglected. We build upon previous work[6] that described the bulging of diffusion couples in a direction transverse to the diffusion direction due to the Kirkendall effect. In that work, the pressure gradient effect was neglected and thus the diffusion and stress analysis were decoupled. Good agreement with experiments was obtained. We extend this simpler approach to diffusion in a single-phase bi-metal strip and in a two-phase bi-metal strip with a moving interface. For the single-phase strip, we arrive at a similar expression as Eq 1 but with a different numerical factor and also obtain a solution using Fourier methods that treats the transition from linear behavior to a final steady state that is important for thin layers. For the two-phase beam, we apply an error function solution to learn that the early time behavior need not be linear. A numerical solution is used to obtain the approach to steady-state behavior.

Models

Single-Phase Beam: General Model

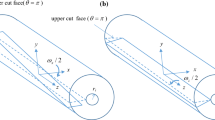
We consider a model that employs a constant molar volume $V_{\text{m}}$ in the sample and consider diffusion in the thin z-direction across a bimetal strip of thickness $\updelta$ (see Fig. 1). The mole fraction, $X_{\text{B}} (z,t)$ has initial conditions

$$ X_{\text{B}} (z,0) = \left\{ {\begin{array}{*{20}c} {X_{\text{B}}^{\text{Bottom}} } \hfill & {{\text{for}}\;0 < z < z_{0} } \hfill \\ {X_{\text{B}}^{\text{Top}} } \hfill & {{\text{for}}\;z_{0} < z < \updelta } \hfill \\ \end{array} } \right. $$

(2)

and satisfies

$$ {\frac{{\partial X_{\text{B}} }}{\partial t}} = \widetilde{D}{\frac{{\partial^{2} X_{\text{B}} }}{{\partial z^{2} }}}, $$

(3)

with the boundary conditions $\partial X_{\text{B}} /\partial z = 0$ at $z = 0$ and $z = \updelta$ where $\tilde{D}$ is the interdiffusion coefficient that is assumed constant.

Fig. 1

The geometry of the bimetal strip. Positive curvature is defined as concave up

The total strain rate $\dot{e}_{ij}^{\text{T}}$ is decomposed into the sum of stress-free, elastic, and plastic parts. The stress-free strain rate $\dot{e}_{ij}^{0}$ is related to the molar volume and the vacancy creation rate $\upsigma_{\text{v}}$, which is equal to the divergence of the vacancy flux $J_{\text{v}}$. The divergence of the flux is related to the difference between the intrinsic diffusion coefficients $D_{\text{A}}$ and $D_{\text{B}}$ and the Laplacian of the mole fraction of component B according to

$$ \dot{e}_{ij}^{0} = {\frac{1}{3}}\updelta_{ij} V_{\text{M}} \upsigma_{\text{v}} = {\frac{1}{3}}\updelta_{ij} V_{\text{M}} \nabla \cdot J_{\text{v}} = {\frac{1}{3}}\updelta_{ij} [D_{\text{B}} - D_{\text{A}} ]\nabla^{2} X_{\text{B}} , $$

(4)

where $[D_{\text{B}} - D_{\text{A}} ]$ has been assumed constant. The stress-free strain is equal to the total strain only if there is no applied stress and/or geometrical constraint of the sample.

A simple model uses a plastic strain rate proportional to the deviatoric stress by the relationship

$$ \dot{e}_{ij}^{\text{P}} = {\frac{1}{2\upeta }}\left[ {\upsigma_{ij} - {\frac{1}{3}}\updelta_{ij} \upsigma_{kk} } \right] , $$

(5)

where $\upeta$ is the viscosity. The elastic strain for an isotropic solid is

$$ e_{ij}^{\text{E}} = {\frac{(1 + \upnu )}{E}}\upsigma_{ij} - {\frac{\upnu }{E}}\upsigma_{kk} \updelta_{ij} $$

(6)

where E is Young’s modulus and $\upnu$ is Poisson’s ratio.

We apply simple beam theory for a spherically bent plate (beam). Only in-plane stresses are considered with $\upsigma_{xx} = \upsigma_{yy} = \upsigma$. Then

$$ \dot{e}_{xx}^{\text{P}} = \dot{e}_{yy}^{\text{P}} = {\frac{\upsigma }{3\upeta }} $$

(7)

and

$$ e_{xx}^{\text{E}} = e_{yy}^{\text{E}} = {\frac{\upsigma (1 - \upnu )}{E}} = {\frac{\upsigma }{2E}} $$

(8)

where the last equality is due to our assuming that the solid is incompressible² ($\upnu = 1/2$).

The total in-plane strain components for a beam with mean curvature $\upkappa (t)$ are

$$ e_{xx}^{\text{T}} (z,t) = e_{yy}^{\text{T}} (z,t) = - \upkappa (t)[z - c(t)], $$

(9)

where $c(t)$ is the z-position of the neutral strain axis.³ The beam curvature is taken as positive when the beam is concave when viewed from positive z. From Eq 4, the in-plane components of the stress-free strain due to the diffusion are

$$ \mathop {\dot{e}}\nolimits_{xx}^{0} = \mathop {\dot{e}}\nolimits_{yy}^{0} = {\frac{\Updelta D}{3}}\,{\frac{{\partial^{2} X_{\text{B}} }}{{\partial z^{2} }}}, $$

(10)

where $\Updelta D = D_{\text{B}} - D_{\text{A}}$. Following only the xx component and using Eq 7–10, the strain rate can be written in the form

$$ {\frac{\text{d}}{{{\text{d}}t}}}\{ - \upkappa (t)[z - c(t)]\} = {\frac{1}{2E}}\,{\frac{\partial \upsigma (z,t)}{\partial t}} + {\frac{1}{3\upeta }}\upsigma (z,t) + {\frac{\Updelta D}{{3\widetilde{D}}}}\,{\frac{{\partial X_{\text{B}} (z,t)}}{\partial t}}. $$

(11)

We next impose the balance of forces and moments standard in simple beam theory,

$$ \int\limits_{0}^{\updelta } {\upsigma (z,t){\text{d}}z = 0} \,,\quad \int\limits_{0}^{\updelta } {z\upsigma (z,t){\text{d}}z = 0} \,, $$

(12)

together with the vanishing of the time derivatives of these expressions. Integrating Eq 11 over $z$, then gives

$$ {\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {\upkappa (t)[z - c(t)]{\text{d}}z} \, = - {\frac{\Updelta D}{{3\widetilde{D}}}}\,{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {X_{\text{B}} (z,t){\text{d}}z} , $$

(13)

and integrating $z$ times Eq 11 with respect to $z$ gives

$$ {\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {z\upkappa (t)[z - c(t)]{\text{d}}z} = - {\frac{\Updelta D}{{3\widetilde{D}}}} \,{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {zX_{B} (z,t){\rm d}z} , $$

(14)

where we have pulled the time derivatives through integrals freely since the limits are independent of time. These expressions can then be integrated in time to produce the two relations

$$ \upkappa (t)\int\limits_{0}^{\updelta } {[z - c(t)]{\text{d}}z} \, = - {\frac{\Updelta D}{{3\widetilde{D}}}}\int\limits_{0}^{\updelta } {[X_{\text{B}} (z,t) - X_{\text{B}} (z,0)]{\text{d}}z} ,\, $$

(15)

$$ \upkappa (t)\int\limits_{0}^{\updelta } {z[z - c(t)]{\text{d}}z} \, = - {\frac{\Updelta D}{{3\widetilde{D}}}}\int\limits_{0}^{\updelta } {z\,[X_{\text{B}} (z,t) - X_{\text{B}} (z,0)]{\text{d}}z}. $$

(16)

Here we have identified the constants of integration in terms of the initial data $X_{\text{B}} (z,0)$, and have assumed that the plate is initially straight, $\upkappa (0) = 0$, and stress-free. Conservation of solute implies that the right hand side of Eq 15 vanishes. This equation then reduces to

$$ \upkappa (t)\left[ {{\frac{{\updelta^{2} }}{2}} - c(t)\updelta } \right] = 0, $$

(17)

and we find $c(t) = \updelta /2$ is at the mid-plane of the beam. Equation 16 then reduces to

$$ \upkappa (t)\left[ {{\frac{{\updelta^{3} }}{3}} - c(t){\frac{{\updelta^{2} }}{2}}} \right] = {\frac{{\updelta^{3} }}{12}}\upkappa (t) = - {\frac{\Updelta D}{{3\widetilde{D}}}}\int\limits_{0}^{\updelta } {z\,[X_{\text{B}} (z,t) - X_{\text{B}} (z,0)]{\text{d}}z}. $$

(18)

We have

$$ \int\limits_{0}^{\updelta } {zX_{\rm B} (z,0){\text{d}}z} = X_{\text{B}}^{\text{Bottom}} \,{\frac{{z_{0}^{2} }}{2}} + X_{\text{B}}^{\text{Top}} \left( {{\frac{{\updelta^{2} }}{2}} - {\frac{{z_{0}^{2} }}{2}}} \right), $$

(19)

and we are left to compute

$$ \int\limits_{0}^{\updelta } {zX_{\text{B}} (z,t){\text{d}}z}. $$

(20)

We note that the mechanical materials parameters, $E$ and $\upeta$, have dropped out of the expression for the time dependence of the curvature of the beam. As in our other work,[6] the stress will, however, depend on the mechanical properties.

Single-Phase Beam: Solution by Fourier Series

Rather than employ standard error function solutions to the diffusion equation that would only be valid for early times, we employ solution by a Fourier series. The solute field is given by

$$ X_{\text{B}} (z,t) = \sum\limits_{n = 0}^{\infty } \,a_{n} \cos{\frac{n\uppi z}{\updelta }}\exp( - n^{2} \uppi^{2} \widetilde{D}t/\updelta^{2} ), $$

(21)

where

$$ a_{0} = [X_{\text{B}}^{\text{Bottom}} \,z_{0} + X_{\text{B}}^{\text{Top}} \,(\updelta - z_{0} )]/\updelta , $$

(22)

and

$$ a_{n} = {\frac{{ - 2\left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right]}}{n\uppi }}\sin{\frac{{n\uppi z_{0} }}{\updelta }}, $$

(23)

for n = 1, 2 …. After combining terms, we find

$$ \updelta \upkappa (t) = 16{\frac{\Updelta D}{{\widetilde{D}}}}\,{\frac{{\left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right]}}{{\uppi^{3} }}}\sum\limits_{{n\;{\text{odd}}}}^{\infty } {{\frac{1}{{n^{3} }}}\sin\,{\frac{{n\uppi z_{0} }}{\updelta }}\left[ {\exp( - n^{2} \uppi^{2} \widetilde{D}t/\updelta^{2} ) - 1} \right]}. $$

(24)

We note that the final curvature is given by

$$ \updelta\upkappa (\infty ) = - 2{\frac{{z_{0} (z_{0} - \updelta )}}{{\updelta^{2} }}} {\frac{\Updelta D}{{\widetilde{D}}}}\left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right], $$

(25)

while expanding the general result (24) to first order in t for small times, we obtain

$$ \upkappa (t) = 4\left[ {{\frac{\Updelta D}{{\updelta^{3} }}}} \right]\left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right]t, $$

(26)

where we have used the result⁴

$$ \,\sum\limits_{{n\,{\text{ odd}}}}^{\infty } {{\frac{1}{n}}\sin{\frac{{n\uppi z_{0} }}{\updelta }}} = {\frac{\uppi }{4}} $$

(27)

Bi-Phase Beam: General Model

Consider the case where the initial condition for $X_{\text{B}}$ is again given by Eq 2 but for $0 \le z \le z_{0}$ the material is $\upalpha$ phase and for $z_{0} \le z \le \updelta$ the material is $\upbeta$ phase. The moving interface between the phases is located at $z^{*}(t)$ with $z^{*}(0) = z_{0}$ and with interface compositions,

$$ X_{\text{B}} (z,t) = \left\{ {\begin{array}{*{20}c} {X_{\text{B}}^{\upalpha \upbeta } } & {{\text{for}}\;z^{ - } = z^{*}(t)} \\ {X_{\text{B}}^{\upbeta \upalpha } } & {{\text{for}}\;z^{ + } = z^{*}(t)} \\ \end{array} } \right.. $$

(28)

The usual conservation equation involving the fluxes also holds at the moving interface.

For this two-phase problem, Eq 10 becomes

$$ \dot{e}_{xx}^{0} = \left\{ \begin{gathered} {\frac{{\Updelta D_{{}}^{\upalpha } }}{3}}{\frac{{\partial^{2} X_{\text{B}}^{\upalpha } }}{{\partial z^{2} }}};\quad 0 < z < z^{*}(t) \hfill \\ {\frac{{\Updelta D_{{}}^{\upbeta } }}{3}}{\frac{{\partial^{2} X_{\text{B}}^{\upbeta } }}{{\partial z^{2} }}};\quad z^{*}(t) < z < \updelta \hfill \\ \end{gathered} \right., $$

(29)

where $\Updelta D_{{}}^{\upalpha }$ and $\Updelta D_{{}}^{\upbeta }$ are the differences $(D_{\text{B}} - D_{\text{A}} )$ in intrinsic diffusion coefficients for each phase. If we assume that the elastic moduli and viscosities of the phases are the same, we can replace Eq 13 and 14 with

$$ \begin{gathered} {\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {\upkappa (t)[z - c(t)]{\text{d}}z} \, = - {\frac{{\Updelta D_{{}}^{\upalpha } }}{{3\tilde{D}^{\upalpha } }}}\left[ {{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{z^{*}(t)} {X_{\text{B}}^{\upalpha } (z,t){\text{d}}z} \, - X_{\text{B}}^{\upalpha } (z^{*}(t),t){\frac{{{\text{d}}z^{*}(t)}}{{{\text{d}}t}}}} \right] \hfill \\ - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{3\tilde{D}^{\upbeta } }}}\left[ {{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{z^{*}(t)}^{\updelta } {X_{\text{B}}^{\upbeta } (z,t){\text{d}}z + X_{\text{B}}^{\upbeta } (z^{*}(t),t){\frac{{{\text{d}}z^{*}(t)}}{{{\text{d}}t}}}} } \right] \hfill \\ \end{gathered} $$

(30)

$$ \begin{gathered} {\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{\updelta } {z\upkappa (t)[z - c(t)]{\text{d}}z} = - {\frac{{\Updelta D_{{}}^{\upalpha } }}{{3\tilde{D}^{\upalpha } }}}\left[ {{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{0}^{z^{*}(t)} {zX_{B}^{\upalpha } (z,t){\text{d}}z - X_{\text{B}}^{\upalpha } (z^{*}(t),t)z^{*}(t){\frac{{{\text{d}}z^{*}(t)}}{{{\text{d}}t}}}} \,} \right] \hfill \\ \quad - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{3\tilde{D}^{\upbeta } }}}\left[ {{\frac{\text{d}}{{{\text{d}}t}}}\int\limits_{z^{*}(t)}^{\updelta } {zX_{\text{B}}^{\upbeta } (z,t){\text{d}}z + X_{\text{B}}^{\upbeta } (z^{*}(t),t)z^{*}(t){\frac{{{\text{d}}z^{*}(t)}}{{{\text{d}}t}}}} } \right] \hfill \\ \end{gathered} $$

(31)

where we have included the effect of the time-dependent limit of integration.

We note that $X_{\text{B}}^{\upalpha } (z^{*}(t),t) = X_{\text{B}}^{\upalpha \upbeta }$ and $X_{\text{B}}^{\upbeta } (z^{*}(t),t) = X_{\text{B}}^{\upbeta \upalpha }$ are constant. Thus both expressions can be integrated with respect to time and in addition the left sides can be integrated with respect to distance yielding

$$ \updelta \upkappa (t)\left[ {{\frac{\updelta }{2}} - c(t)} \right] = P(t) $$

(32)

$$ \updelta^{2} \upkappa (t)\left[ {{\frac{\updelta }{3}} - {\frac{c(t)}{2}}} \right] = Q(t) $$

(33)

where

$$ \begin{gathered} P(t) = - {\frac{{\Updelta D^{\upalpha } }}{{3\tilde{D}^{\upalpha } }}}\left[ {\int\limits_{0}^{z^{*}(t)} {\left[ {X_{\text{B}}^{\upalpha } (z,t) - X_{\text{B}}^{\upalpha } (z,0)} \right]{\text{d}}z} \, - X_{\text{B}}^{\upalpha \upbeta } \left[ {z^{*}(t) - z_{0} } \right]} \right] \hfill \\ - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{3\tilde{D}{}^{\upbeta }}}}\left[ {\int\limits_{z^{*}(t)}^{\updelta } {\left[ {X_{\text{B}}^{\upbeta } (z,t) - X_{\text{B}}^{\upbeta } (z,0)} \right]{\text{d}}z} + X_{\text{B}}^{\upbeta \upalpha } [z^{*}(t) - z_{0} ]} \right] \hfill \\ \end{gathered} $$

(34)

$$ \begin{gathered} Q(t) = - {\frac{{\Updelta D^{\upalpha } }}{{3\tilde{D}^{\upalpha } }}}\left[ {\int\limits_{0}^{z^{*}(t)} {z\left[ {X_{\text{B}}^{\upalpha } (z,t) - X_{\text{B}}^{\upalpha } (z,0)} \right]{\text{d}}z} \, - {\frac{{X_{\text{B}}^{\upalpha \upbeta } }}{2}}\left[ {{z^{*}}^{2} (t) - z_{0}^{2} } \right]} \right] \hfill \\ - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{3D^{\upbeta } }}}\left[ {\int\limits_{z^{*}(t)}^{\updelta } {z\left[ {X_{\text{B}}^{\upbeta } (z,t) - X_{\text{B}}^{\upbeta } (z,0)} \right]{\text{d}}z} + {\frac{{X_{\text{B}}^{\upbeta \upalpha } }}{2}}[{z^{*}}^{2} (t) - z_{0}^{2} ]} \right] \hfill \\ \end{gathered} $$

(35)

Solving for $\upkappa (t)$ and $c(t)$, we obtain

$$ \begin{gathered} {\frac{{\updelta^{3}\upkappa (t)}}{12}} = Q(t) - {\frac{\updelta }{2}}P(t) \hfill \\ c(t) - {\frac{\updelta }{2}} = {\frac{P(t)}{{6\left[ {P(t) - {\frac{2}{\updelta }}Q(t)} \right]}}} \hfill \\ \end{gathered} $$

(36)

Note that the strain neutral axis position $c(t)$ is time-dependent. The equation for the curvature becomes

$$ \begin{gathered} {\frac{{\updelta^{3}\upkappa (t)}}{12}} = - {\frac{{\Updelta D^{\upalpha } }}{{3\tilde{D}^{\upalpha } }}}\int\limits_{0}^{z^{*}(t)} {\left\{ {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {X_{\text{B}}^{\upalpha } (z,t) - X_{\text{B}}^{\upalpha } (z,0)} \right]\,} \right\}{\text{d}}z} \hfill \\ - {\frac{{\Updelta D^{\upbeta } }}{{3\tilde{D}^{\upbeta } }}}\int\limits_{z^{*}(t)}^{\updelta } {\left\{ {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {X_{\text{B}}^{\upbeta } (z,t) - X_{\text{B}}^{\upbeta } (z,0)} \right]} \right\}{\text{d}}z} \hfill \\ + {\frac{1}{6}}\left[ {{\frac{{\Updelta D^{\upalpha } }}{{\tilde{D}^{\upalpha } }}}X_{\text{B}}^{\upalpha \upbeta } - {\frac{{\Updelta D^{\upbeta } }}{{\tilde{D}^{\upbeta } }}}X_{\text{B}}^{\upbeta \upalpha } } \right][z^{*}(t) - z_{0} ][z^{*}(t) + z_{0} - \updelta ] \hfill \\ \end{gathered} $$

(37)

We are left to evaluate the integrals from the diffusion solution. These integrals are evaluated for the final state when all diffusion has stopped and an equilibrium state has been achieved in Section 2.4. The time dependence will be evaluated in two ways: analytically for early time using the error function solution for a moving interface in the Appendix (summarized in Section 2.5) and by numerically solving the diffusion equation as described in Section 2.6.

Bi-Phase Beam: Final Curvature

Equation 37 can be evaluated for the final equilibrium composition profiles and the final interface position, $z_{\text{f}}$ obtained from a simple solute balance. The final curvature $\upkappa_{\text{f}}$ is

$$ \begin{gathered} {\frac{{\updelta^{3} \upkappa_{\text{f}} }}{2}} = z_{\text{f}} (z_{\text{f}} - \updelta )\left\{ { - {\frac{{\Updelta D^{\upalpha } }}{{\tilde{D}^{\upalpha } }}}\left[ {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right] + {\frac{{\Updelta D^{\upbeta } }}{{\tilde{D}^{\upbeta } }}}\left[ {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right]} \right\} \hfill \\ + (z_{\text{f}} - z_{0} )(z_{\text{f}} + z_{\text{o}} - \updelta )\left\{ {{\frac{{\Updelta D^{\upalpha } }}{{\tilde{D}^{\upalpha } }}}X_{\text{B}}^{\upalpha \upbeta } - {\frac{{\Updelta D^{\upbeta } }}{{\tilde{D}^{\upbeta } }}}X_{\text{B}}^{\upbeta \upalpha } } \right\} \hfill \\ \end{gathered} $$

(38)

with

$$ z_{\text{f}} = {\frac{{\updelta \left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\upbeta \upalpha } } \right] + z_{0} \left[ {X_{\text{B}}^{\text{Bottom}} - X_{\text{B}}^{\text{Top}} } \right]}}{{X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } }}} $$

(39)

Bi-Phase Beam: Analytical Solution for Early Time

In the appendix, it is shown that for early time, $t \ll [\min (z_{0} ,\updelta - z_{0} )]^{2} /\max (\tilde{D}^{\upalpha } ,\tilde{D}^{\upbeta } )$, Eq 37 can be written as

$$ {\frac{{\updelta^{3} \upkappa (t)}}{12}} = A\sqrt t + Bt, $$

(40)

with A and B given by Eq A17 and A18 and repeated here,

$$ \begin{gathered} A \approx {\frac{\updelta }{3\sqrt \uppi }}\,{\frac{{(1 - 2z_{0} /\updelta )}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}\left\{ {\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right)\left[ {{\frac{{\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}\left( {2X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right) - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{r\sqrt {\tilde{D}^{\upbeta } } }}}X_{\text{B}}^{\upbeta \upalpha } } \right]} \right. \hfill \\ \left. { - \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)\left[ {{\frac{{\Updelta D^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}\left( {2X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upalpha \upbeta } } \right) - {\frac{{r\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}X_{\text{B}}^{\upalpha \upbeta } } \right]} \right\} \hfill \\ \end{gathered} $$

(41)

$$ B \approx {\frac{1}{3}}\left[ {\Updelta D^{\upalpha } \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right) - \Updelta D^{\upbeta } \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)} \right], $$

(42)

where $r^{2} = \tilde{D}^{\upbeta } /\tilde{D}^{\upalpha }$. This expression holds only for small values of dimensionless deviations from the equilibrium interface compositions for each phase; i.e., $|S^{\upalpha } | \ll 1$ and $|S^{\upbeta } | \ll 1$ with

$$ \begin{gathered} S^{\upalpha } = {\frac{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right)}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}, \hfill \\ S^{\upbeta } = {\frac{{\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}. \hfill \\ \end{gathered} $$

(43)

Values for the parameters A and B for larger values of $S^{\upalpha }$ and $S^{\upbeta }$ are given in Eq A12 and A13. We note the presence of a term proportional to $\sqrt t$ in the result for the two-phase beam not present in the single-phase beam. The term vanishes when the initial interface is centered in the beam, $z_{0} = \updelta /2$.

Bi-Phase Beam: Numerical Solution

To determine the complete time behavior that spans the early time result and the final equilibrium result, numerical solution to the diffusion problem is required. We use a change of variables from $(z,t)$ to $(y,t)$ that fixes the interface location. We define

$$ y = \left\{ {\begin{array}{*{20}c} {[z - z^{*}(t)]/z^{*}(t)} \hfill & {0 \le z \le z^{*}(t)} \hfill \\ {[z - z^{*}(t)]/[\updelta - z^{*}(t)]} \hfill & {z^{*}(t) \le z \le \updelta } \hfill \\ \end{array} } \right. $$

(44)

and set $u^{\upalpha } (y,t) = X_{\text{B}}^{\upalpha } (z,t)$ for $- 1 \le y \le 0$ and $u^{\upbeta } (y,t) = X_{\text{B}}^{\upbeta } (z,t)$ for $0 \le y \le 1$; the interface is then always located at $y = 0$. The solution to the transformed equations for $u^{\upalpha } (y,t)$ and $u^{\upbeta } (y,t)$ is then obtained using a finite difference scheme to discretize in space, coupled to an ordinary differential equation solver in time. To avoid resolving the steep spatial gradients in the concentration profile near the interface at short times, the initial conditions for the numerical solution are obtained from the similarity solution (Section A1) at a time $t > 0$ that is large enough that the steep gradients have decayed, but small enough that the end effects associated with the finite couple are still insignificant. Results from this numerical solution (composition profiles and interface position) are then used to evaluate the curvature expression (Eq 37).

Results and Discussion

Single-Phase Beam

Evaluation of the general result (Eq 24) is made for materials parameters corresponding to the experiments of Daruka et al.[2] for diffusion couple beams made initially of pure Ti and Zr and annealed at 1223 K. Both components are BCC and are completely soluble in each other. Taking component A as Ti on the bottom and component B as Zr on the top, $X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} = 1.0$. Further we take $\updelta = 0.2$  mm $\Updelta D = D_{\text{Zr}} - D_{\text{Ti}} = 6 \times 10^{ - 14}$ m² s⁻¹ and $\widetilde{D} = 1.6 \times 10^{ - 13}$ m² s⁻¹ (as measured by Daruka et al.,[2] giving $\Updelta D/\widetilde{D} = 0.375$). Figure 2 shows results for several values of the location of the initial discontinuity, $z_{0}$. For $z_{0} = \updelta /2$, the predicted curve is approximately linear for $0 < t\widetilde{D}/\updelta^{2} < 0.05$, and has reached its limiting value by $t\widetilde{D}/\updelta^{2} = 0.5$. The dashed lines are the linear approximations for early time (Eq 26) and the constant limiting values for late time (Eq 25) for each value of $z_{0}$.

Fig. 2

Single-phase beam results: dimensionless curvature $\updelta \upkappa$ vs. dimensionless time tD/δ² for the indicated values of z _o /δ. The dashed lines are the initial approximation which is independent of z _o /δ and the long-time limits and ΔD/d = 0.375 and $X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} = 1.0$

In agreement with Daruka et al.,[2] the slope of the linear portion does not depend on the interdiffusion coefficient as seen in Eq 26. It also does not depend on the position of the initial interface. However, the final curvature given by Eq 25 does depend on the initial position of the interface through the factor $z_{0} (\updelta - z_{0} )/\updelta^{2}$. This factor is at a maximum if the initial interface is centered in the beam and decreases as the initial position is situated on either side of center. The time $t^{*}$ of the intersection of the linear curve and the limiting values is given by

$$ \tilde{D}t^{*}/ \updelta^{2} = {\frac{1}{2}} \,{\frac{{z_{0} }}{\updelta }}\left( {1 - {\frac{{z_{0} }}{\updelta }}} \right) . $$

(45)

Thus the valid time range of the linear form is reduced as the initial interface is placed farther off center as one would expect.

The physical understanding of the general result is as follows. Because the top of the diffusion couple is B-rich and B is the fast diffuser, the curvature goes positive; the beam becomes more concave with time when viewed from positive z or the B side (See Fig. 1). Component B has left the top of the beam faster than it has been replaced by component A, requiring the top of the beam to decrease in volume (lose lattice sites). At long times, the diffusion process slows as the sample becomes uniform in composition and reaches a final curvature. Measurement of the final curvature would require experimental times much greater than $t^{*}$ derived from Eq 45.

It is of interest to compare our result for early time, Eq 26, to the analytical result of Ref. 2 given in Eq 1. Evaluating their expression for the concentration-weighted intrinsic diffusion coefficients given in Ref. 2 for our case of constant molar volume and constant intrinsic diffusion coefficients, one obtains

$$ \bar{D}_{\text{i}} = \left( {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right)D_{\text{i}} ,$$

(46)

so that their Eq 1 becomes

$$ \upkappa (t) = 6\,{\frac{{\Updelta D\left[ {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right]}}{{\updelta^{3}}}}\,t,$$

(47)

which differs from our result only by the numerical factor of six rather than four.

The difference in the models is due to different assumptions about the beam shape. To correspond to their experimental conditions, the model of Daruka et al. force a cylindrical shape by applying a moment along one edge of a rectangular plate to keep it straight (e.g., to the left in Fig. 1). In contrast, our results apply to a beam that is not so clamped but is free to bend in both orthogonal directions into a spherical shape; i.e., no such moment is applied. Indeed the experiment of Daruka et al. note deviations from a cylindrical shape as a reason for the variation of measured slopes in curvature versus time plots for diffusion conducted at 1223 K (their Fig. 10). They note that the largest slope refers to the ideal case that experimentally was closest to the cylindrical shape and the lower slopes to when some curvature in the perpendicular direction was observed at the end away from the clamp. The ratio of their highest to lowest slopes is approximately 2.8, while the ratio of cylindrical to spherical numerical factors from the models is 6/4 = 1.5. Thus a significant portion of their range of slopes can be understood through an examination of the difference between the cylindrical and spherical cases. It is not clear however why there is a transition experimentally from cylindrical curvature near the clamp to a doubly curved surface away from the clamp.

Two-Phase Beam

If the original interface is at the middle of the sample, $z_{0} = \updelta /2$, the analysis of the two-phase beam for early time retains the general result of the single-phase beam that the curvature is linear in time and does not depend on the interdiffusion coefficient(s). Using the value for $B$ given by Eq 42 and $A = 0$ in Eq 40 yields

$$ \upkappa (t) = {\frac{12Bt}{{\updelta^{3} }}} = {\frac{4}{{\updelta^{3} }}}\left[ {\Updelta D^{\upalpha } \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right) - \Updelta D^{\upbeta } \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)} \right]t. $$

(48)

In the limit of the single-phase beam and with $\Updelta D_{{}}^{\upalpha } = \Updelta D_{{}}^{\upbeta } = \Updelta D$ the slope is proportional to $\Updelta D( {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} })$, the result obtained for the single-phase beam. Equation 45 may provide experimentalists a new method to gain intrinsic diffusion data $(\Updelta D^{\upalpha } {\text{ and }}\Updelta D^{\upbeta } )$ by measuring beam curvatures with two-phase beams. As an aside, it is remarkable to note that except for the numerical factor, Eq 48 could have been obtained by evaluation of the integrals for the concentration-weighted diffusion coefficients (Eq 1) of Daruka et al.[2] even though it was derived for a single-phase beam.

If the original interface is not the middle of the sample, $z_{0} \ne \updelta /2$, a $\sqrt t$ term that depends on the initial interface position $z_{0}$ is obtained. The coefficient of the $\sqrt t$ term is given by the parameter $A$ given by Eq 41. Figure 3 shows results for two-phase beam for the parameters given in Table 1. The dashed curves highlight the interplay of the $\sqrt t$ and linear terms using Eq 40-42. If the initial interface is situated at the center of the beam, $z_{0} = \updelta /2$, the initial behavior is linear in time. Because both $\Updelta D_{\upalpha }$ and $\Updelta D_{\upbeta }$ were taken positive, the curvature is positive and increases linearly with time. If the initial interface is toward the bottom of the beam, $z_{0} /\updelta$ small, the curvature increases faster than linearly with time. If the initial interface is toward the top of the beam, $z_{0} /\updelta$ nearer unity, the curvature goes negative and then slightly flattens. We have also included the values of the final curvature from Eq 38 and 39 in Fig. 3 as horizontal dashed lines. The results of the full numerical analysis (solid curves) predict a gradual transition from the approximate solution at early time to the final curvatures indicated. The special case of $z_{0} = 0.649\;\updelta$ chosen to give zero final curvature, has a significant nonmonotonic behavior with curvature going negative at early time followed by a gradual return to zero curvature.

Fig. 3

Two-phase beam results: $\updelta {\kern 1pt} \upkappa (t)$ vs. $\tilde{D}_{\upbeta } t/\updelta^{2}$ for four positions, $z_{0} /\updelta$, of the initial $\upalpha /\upbeta$ interface. Three lines are shown for each value $z_{0} /\updelta$: The final curvature (dashed, horizontal lines); the curvature from the early time expression (dashed curves); and the fully numerical solution (solid lines)

Table 1 Parameters for Fig. 3 (All units SI)

The physical understanding of the cases evaluated is as follows. Component B leaves the top of the beam and the interface moves toward the top as the $\upbeta$ phase dissolves. There is no diffusion in the $\upbeta$ phase because we have taken $X_{\text{B}}^{\text{Top}} = X_{\text{B}}^{\upbeta \upalpha }$. The $\upalpha$ phase becomes richer in component B on average with no decrease in component A, thus lattice sites must be created by vacancy emission from defects within the $\upalpha$ phase that can be filled with the extra B atoms. This causes an expansion of the beam below the $\upalpha \upbeta$ interface. If the initial interface is near the bottom of the beam, the bottom part of the beam expands (adds lattice sites) making the curvature go positive more quickly than if the interface had been at the middle. If the initial interface is near the top of the beam, the top part of the beam expands making the curvature go negative at early time. At later time as the diffusion spreads farther into the lower half of the beam, expansion occurs there that reverses the direction of bending.

Conclusions

The bending of binary alloy single-phase and two-phase beams due to diffusion across the beam has been computed for dissimilar lattice diffusion rates of the two components. The initial beams contain a step function composition profile and results are given for the full time range until the beam is uniform in composition or an equilibrium two-phase mixture is obtained. Analytical expressions are available for the final curvature in both cases. At early time, the curvature of a single-phase beam is linear in time, as also found by other researchers. However, the coefficient of proportionality varies depending on whether the beam is allowed to bend in two planes or only in one. The curvature of the two-phase beam for early time is linear in time only if the initial composition discontinuity is centered in the beam; otherwise the curvature goes as the square root of time at early time. Nonmonotonic behavior for the curvature-time relation can also occur for two-phase beams.

Appendix: Analytical Evaluation of the Beam Curvature for Early Time Using the Error Function Solution

The Similarity Error Function Diffusion Solution for a Moving Interface

To determine the behavior of the bi-phase beam for early time $t \ll [\min (z_{0} ,\updelta - z_{0} )]^{2}/\max (\tilde{D}^{\upalpha } ,\tilde{D}^{\upbeta } )$, we use the error function solution for a two-phase diffusion couple obtained from Sekerka and Wang,[7] for example, with far field compositions given by $X_{\text{B}}^{\upalpha \infty } = X_{\text{B}}^{\text{Bottom}}$ and $X_{\text{B}}^{\upbeta \infty } = X_{\text{B}}^{\text{Top}}$. For interdiffusion coefficients $\tilde{D}^{\upalpha }$ and $\tilde{D}^{\upbeta }$ for the two phases (assumed constant) and using $r^{2} = \tilde{D}^{\upbeta } /\tilde{D}^{\upalpha }$, the composition profiles are

$$ \begin{gathered} X_{\text{B}}^{\upalpha } (z,t) = X_{\text{B}}^{\upalpha \infty } + \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upalpha \infty } } \right){\frac{{1 + {\text{erf}}\left( {{{\left( {z - z_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {z - z_{0} } \right)} {\sqrt {4\tilde{D}^{\upalpha } t} }}} \right. \kern-\nulldelimiterspace} {\sqrt {4\tilde{D}^{\upalpha } t} }}} \right)}}{{1 + {\text{erf}}(rK)}}}, \hfill \\ X_{\text{B}}^{\upbeta } (z,t) = X_{\text{B}}^{\upbeta \infty } + \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upbeta \infty } } \right){\frac{{1 - {\text{erf}}\left( {{{\left( {z - z_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {z - z_{0} } \right)} {\sqrt {4\tilde{D}^{\upbeta } t} }}} \right. \kern-\nulldelimiterspace} {\sqrt {4\tilde{D}^{\upbeta } t} }}} \right)}}{{1 - {\text{erf}}(K)}}}, \hfill \\ \end{gathered} $$

(A1)

with

$$ z^{*} (t) - z_{0} = K\sqrt {4\tilde{D}^{\upbeta } t} . $$

(A2)

Here $K$ is the root of

$$ K + {\frac{1}{\sqrt \uppi }}\,{\frac{1}{r}}S^{\upalpha } \left[ {{\frac{{\exp ( - r^{2} K^{2} )}}{{1 + {\text{erf}}(rK)}}}} \right] + {\frac{1}{\sqrt \uppi }}\,S^{\upbeta } \left[ {{\frac{{\exp ( - K^{2} )}}{{1 - {\text{erf}}(K)}}}} \right] = 0, $$

(A3)

with dimensionless deviations from the equilibrium compositions for each phase given by

$$ \begin{gathered} \hfill S^{\upalpha } = {\frac{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upalpha \infty } } \right)}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}, \\ \hfill S^{\upbeta } = {\frac{{\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upbeta \infty } } \right)}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}. \\ \end{gathered} $$

(A4)

It can be shown that if $\tilde{D}^{\upalpha } = \tilde{D}^{\upbeta }$ and $X_{\text{B}}^{\upalpha \upbeta } = X_{\text{B}}^{\upbeta \upalpha } = ( {X_{\text{B}}^{\upalpha \infty } + X_{\text{B}}^{\upbeta \infty } } )/2$, then $K = 0$ and we recover the solution for the single-phase diffusion problem. Further simplification is possible for small deviations of the initial conditions from the equilibrium interface compositions; i.e., $(S_{\upalpha } + S_{\upbeta } ) \ll {\frac{\uppi }{2}}$ and for $r$ not too large,

$$ K \approx - {\frac{1}{\sqrt \uppi }}\left( {S^{\upalpha } {\frac{1}{r}} + S^{\upbeta } } \right) , $$

(A5)

i.e.,

$$ K \approx - {\frac{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upalpha \infty } } \right){\frac{1}{r}} + \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upbeta \infty } } \right)}}{{\sqrt \uppi \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}} . $$

(A6)

Curvature

Returning to the beam deflection problem and by noting that $X_{\text{B}}^{\upalpha } (z,0) = X_{\text{B}}^{\upalpha \infty }$ and $X_{\text{B}}^{\upbeta } (z,0) = X_{\text{B}}^{\upbeta \infty }$, the integrals in Eq 37 can be written

$$ \begin{gathered} \int\limits_{0}^{z^{*}(t)} {\left\{ {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {X_{\text{B}}^{\upalpha } (z,t) - X_{\text{B}}^{\upalpha } (z,0)} \right]} \right\}{\text{d}}z} = B_{\upalpha } \int\limits_{0}^{z^{*}\left( t \right)} {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {1 + {\text{erf}}\left( {{{\left( {z - z_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {z - z_{0} } \right)} {\sqrt {4\tilde{D}^{\upalpha } t} }}} \right. \kern-\nulldelimiterspace} {\sqrt {4\tilde{D}^{\upalpha } t} }}} \right)} \right]} {\text{d}}z, \hfill \\ \int\limits_{z^{*}(t)}^{\updelta } {\left\{ {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {X_{\text{B}}^{\upbeta } (z,t) - X_{\text{B}}^{\upbeta } (z,0)} \right]} \right\}{\text{d}}z} = B_{\upbeta } \int\limits_{z^{*}(t)}^{\updelta } {\left\{ {\left( {z - {\frac{\updelta }{2}}} \right)\left[ {1 - {\text{erf}}\left( {{{\left( {z - z_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {z - z_{0} } \right)} {\sqrt {4\tilde{D}^{\upbeta } t} }}} \right. \kern-\nulldelimiterspace} {\sqrt {4\tilde{D}^{\upbeta } t} }}} \right)} \right]} \right\}{\text{d}}z,} \hfill \\ \end{gathered} $$

(A7)

where

$$ \begin{gathered} B_{\upalpha } = {\frac{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upalpha \infty } } \right)}}{{1 + {\text{erf}}(rK)}}}, \hfill \\ B_{\upbeta } = {\frac{{\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upbeta \infty } } \right)}}{{1 - {\text{erf}}(K)}}}. \hfill \\ \end{gathered} $$

(A8)

By performing the integrals above, one obtains

$$ {\frac{{\updelta^{3} \upkappa (t)}}{12}} = f(t), $$

(A9)

where $f(t)$ has the form

$$ f(t) = a + b\sqrt t + ct + d\exp ( - 1/t)\sqrt t + k\,{\text{erf}}(1/\sqrt t ) + m\,t\,{\text{erf}}(1/\sqrt t ) $$

(A10)

which can expanded for lowest powers of $t$ as

$$ {\frac{{\updelta^{3} \upkappa (t)}}{12}} = A\sqrt t + Bt, $$

(A11)

where the constant term drops out. One obtains for the constants A and B

$$ \begin{gathered} A = {\frac{\updelta }{3}}\left( {1 - {\frac{{2z_{0} }}{\updelta }}} \right)\left\{ {{\frac{{\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}} \right.\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right)\left( {{\frac{{\exp \left( { - r^{2} K^{2} } \right)}}{{\sqrt \uppi (1 + {\text{erf}}(rK))}}} + rK} \right) \hfill \\ + {\frac{{\Updelta D_{{}}^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)\left( {{\frac{{\exp \left( { - K^{2} } \right)}}{{\sqrt \uppi \left( {1 - {\text{erf}}(K)} \right)}}} - K} \right) \hfill \\ + \left. {\left[ {{\frac{{\Updelta D_{{}}^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}\,X_{\text{B}}^{\upbeta \upalpha } - {\frac{{r\Updelta D^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}\,X_{\text{B}}^{\upalpha \upbeta } } \right]K} \right\} \hfill \\ \end{gathered} $$

(A12)

and

$$ \begin{gathered} B = {\frac{{\Updelta D_{{}}^{\upalpha } }}{3}}\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right)\left[ {(1 - 2r^{2} K^{2} ) - {\frac{2}{\sqrt \uppi }}\,{\frac{{rK\exp ( - r^{2} K^{2} )}}{{1 + {\text{erf}}(rK)}}}} \right] \hfill \\ - {\frac{{\Updelta D^{\upbeta } }}{3}}\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)\left[ {(1 - 2K^{2} ) + {\frac{2}{\sqrt \uppi }}\,{\frac{{K\exp ( - K^{2} )}}{{1 - {\text{erf}}(K)}}}} \right] \hfill \\ + {\frac{2}{3}}\left[ {r\Updelta D^{\upalpha } X_{\text{B}}^{\upalpha \upbeta } - \Updelta D^{\upbeta } X_{\text{B}}^{\upbeta \upalpha } } \right]K^{2} \hfill \\ \end{gathered} $$

(A13)

where we have reintroduced $X_{\text{B}}^{\text{Bottom}} = X_{\text{B}}^{\upalpha \infty }$ and $X_{\text{B}}^{\text{Top}} = X_{\text{B}}^{\upbeta \infty }$. Note that only the $\sqrt t$ term depends on the initial interface position $z_{0}$ in this expansion. If the original interface is at the middle of the sample, $z_{0} = \updelta /2$, $A = 0$ and the curvature is linear in time as in the single-phase problem. Also, in the limit of the single-phase problem, $X_{\text{B}}^{\upalpha \upbeta } = X_{\text{B}}^{\upbeta \upalpha } = ( {X_{\text{B}}^{\text{Bottom}} + X_{\text{B}}^{\text{Top}} } )/2$ and $\tilde{D}^{\upalpha } = \tilde{D}^{\upbeta }$, $K = 0$ and one obtains $A = 0$ no matter the value of $z_{0}$ in agreement with the result for the single-phase beam. Setting $\Updelta D_{{}}^{\upalpha } = \Updelta D_{{}}^{\upbeta } = \Updelta D$ in this last case gives

$$ B = {\frac{1}{3}}\Updelta D\left( {X_{\text{B}}^{\text{Top}} - X_{\text{B}}^{\text{Bottom}} } \right). $$

(A14)

and we recover the early time result obtained in Section 2.2.

Curvature for Small $S^{ \upalpha }$ and $S^{ \upbeta }$

The results, Eq A12 and A13, can be approximated to first order in K yielding simpler expressions for A and B,

$$ \begin{gathered} A \approx {\frac{\updelta }{3}}\left( {1 - {\frac{{2z_{0} }}{\updelta }}} \right)\left\{ {{\frac{{\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}} \right.\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Top}} } \right)\left( {{\frac{1}{\sqrt \uppi }} - \left[ {{\frac{2}{\uppi }} - 1} \right]rK} \right) + {\frac{{\Updelta D_{{}}^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}\left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Bottom}} } \right)\left( {{\frac{1}{\sqrt \uppi }} + \left[ {{\frac{2}{\uppi }} - 1} \right]K} \right) \hfill \\ + \left. {\left[ {{\frac{{\Updelta D^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}X_{\text{B}}^{\upbeta \upalpha } - {\frac{{r\Updelta D^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}X_{\text{B}}^{\upalpha \upbeta } + } \right]K} \right\} \hfill \\ \end{gathered} $$

(A15)

$$ B \approx {\frac{1}{3}}\left[ {\Updelta D^{\upalpha } \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right) - \Updelta D^{\upbeta } \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)} \right] - K{\frac{2}{3\sqrt \uppi }}\left[ {r\Updelta D^{\upalpha } \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right) + \Updelta D^{\upbeta } \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)} \right] $$

(A16)

For small values of $S^{\upalpha }$ and $S^{\upbeta }$; i.e., small deviations of the far field compositions from the equilibrium interface conditions, one can use Eq A6 to obtain to first order in $( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } )$ and $( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} })$,

$$ \begin{gathered} A \approx {\frac{\updelta }{3\sqrt \uppi }} \,{\frac{{\left( {1 - 2z_{0} /\updelta } \right)}}{{\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right)}}}\left\{ {\left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right)\left[ {{\frac{{\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}\left( {2X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\upbeta \upalpha } } \right) - {\frac{{\Updelta D_{{}}^{\upbeta } }}{{r\sqrt {\tilde{D}^{\upbeta } } }}}X_{\text{B}}^{\upbeta \upalpha } } \right]} \right. \hfill \\ \left. { - \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)\left[ {{\frac{{\Updelta D_{{}}^{\upbeta } }}{{\sqrt {\tilde{D}^{\upbeta } } }}}\left( {2X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\upalpha \upbeta } } \right) - {\frac{{r\Updelta D_{{}}^{\upalpha } }}{{\sqrt {\tilde{D}^{\upalpha } } }}}X_{\text{B}}^{\upalpha \upbeta } } \right]} \right\} \hfill \\ \end{gathered} $$

(A17)

$$ B \approx {\frac{1}{3}}\left[ {\Updelta D^{\upalpha } \left( {X_{\text{B}}^{\upalpha \upbeta } - X_{\text{B}}^{\text{Bottom}} } \right) - \Updelta D^{\upbeta } \left( {X_{\text{B}}^{\upbeta \upalpha } - X_{\text{B}}^{\text{Top}} } \right)} \right] $$

(A18)