Introduction

Hybrid construction methods, in which (light) metals and composite materials are brought together, are regarded as promising lightweight construction strategies. In the implementation of these concepts, the focus is on the sensible combination of the two materials, which are aluminum and CFRP [1, 2] in this case study. In the area of joining partners made of fiber composites, thermoset CFRP matrix systems exhibit disadvantageous properties such as brittleness, time-consuming production cycles and limited temperature resistance [3]. This makes them unsuitable for using in die casting process. Thermoplastic matrix systems such as polyetheretherketones (PEEK), on the other hand, have higher temperature resistance, toughness and the possibility to be produced faster [4]. Despite the high level of innovation used in production processes to achieve highly resilient and ultra-lightweight thermoset or thermoplastic CFRP structures and near-net-shape, economical die-cast aluminum components [5, 6], conventional mechanical or adhesive joining techniques are used in most cases for the manufacture of hybrid components made of aluminum and CFRP.

However, these joining techniques have several disadvantages. And this is why new types of joining technologies are being researched in different areas [7, 8]. For example, there may be changes in material properties within the heat-affected zone in welded joints or uneven stress transfer in the area of riveted joints [9]. Due to different material properties of the two materials, the joining technology for combining them plays a decisive role. The mechanical characterization of the boundary layer is also of decisive importance here [10].

In the present work, a methodology is developed to describe the failure behavior of a hybrid component made of aluminum and CFRP with a thermoplastic boundary layer under mode I loading, using the cohesive zone model. In addition to the performance of the fracture mechanical tests and the subsequent evaluation, the determination of the fracture mechanical parameters based on the test results is described. The focus of the subsequent analyses, which are performed using the commercial finite element software ABAQUS/Standard, was on the determination of the parameters of the cohesive zone model in order to ensure a high degree of agreement between the numerical model and the experimental results.

Experimental Work

The single-lap test specimens produced for the fracture mechanical tests are made of CFRP sheets with a length of 100 mm, a width of 40 mm and a thickness of 1.55 mm. These sheets are made of carbon fiber fabric and a PEEK matrix, partially coated with (250 µm thick) films of PEEK. They are casted on one side with aluminum melt in a die casting process. The joining partner made of aluminum has the dimensions 100 × 40 × 10 mm. The resulting material composite is shown in Fig. 1.

Fig. 1
figure 1

Single-lap specimen

Full size image

Wedge Test

One of the most widely used methods for identifying the constitutive parameters of the cohesive zone model is to perform crack propagation tests for the respective fracture modes [11]. A method for determining the adhesive properties of an adhesive bond of surface-treated aluminum sheets with standardized dimensions has been developed in the wedge test. This is carried out in a modified form in accordance with standard ASTM D3762 to determine the critical energy release rate for fracture mode I. For this purpose, samples of the hybrid composite (single-lap) were used which overlapped on one side. The thickness of the 40 mm × 100 mm aluminum joining partners was 10 mm. The CFK sheet metal with a thickness of 1.5 mm was cut off directly at the end of the overlap area. Between the two joining partners, the melted PEEK foil with a thickness of 0.25 mm is located on the overlapping area with a size of 40 mm × 40 mm. Before clamping the aluminum joining partner, a crack of 2 mm length was made with a razor blade in the area where the wedge is to be driven in. A wedge with a width of 40 mm, thickness of 6 mm and an angle of 30° was then inserted into it at a speed of 5 mm per minute. The testing machine was used to measure the reaction force and feed path.

The setup is shown in Fig. 2.

Fig. 2
figure 2

Principle sketch of the experimental setup

Full size image

Modeling

The experiments were modeled using ABAQUS. The mechanical model for investigating the delamination process is shown schematically in Fig. 3. The model consists of three bodies. The 40 mm × 40 mm large and 1.55 mm thick CFRP sheet, which is connected to the 40 mm × 40 mm large and 0.25 mm thick PEEK layer underneath by using a tie constraint. This in turn is connected via a cohesive zone with the underlying aluminum part with the dimensions 40 mm × 10 mm × 100 mm.

Fig. 3
figure 3

Finite element model with boundary conditions

Full size image

Within the scope of the investigations, an elastic–plastic material model for the aluminum joining partner, an elastic material model for the PEEK boundary layer, and an orthotropic material model for the CFRP are used. The parameters of the material models are summarized in the following tables.

The discretization of the three components is done by continuum elements of type C3D8R. The C3D8R element is an eight node, three dimensional continuum stress/displacement element, with reduced integration. For the cohesive zone a surface-based interaction was selected.

Figure 3 shows the geometrical boundary conditions. Here, the nodes at the bottom of the composite are fixed in all directions. The displacement of the wedge is initiated at the back of the wedge using a reference point.

Cohesive Zone Modeling

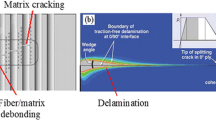
The cohesive zone model [12,13,14] is one of the most widely used tools to describe fracture processes in interfaces. It can be used to describe the elastic behavior of the interface, crack initiation under load, crack propagation and complete failure of the interface for the respective fracture mode [15]. The surface-based damage model with bilinear constitutive law used here [16] is fully described by the parameter K, which describes the initial stiffness of the cohesive zone, the critical stress at crack initiation and the critical energy release rate. When the critical stress is reached, damage initiation begins. As soon as the critical separation is reached, the boundary layer is completely separated. Figure 4 shows a typical traction–separation response with a failure mechanism.

Fig. 4
figure 4

Bilinear constitutive model

Full size image

The damage initiation is described in the following investigations by a quadratic nominal stress criterion as follows.

$$\left\{ {\frac{{\left\langle {t_{n} } \right\rangle }}{{t_{n}^{0} }}} \right\}^{2} + \left\{ {\frac{{t_{s} }}{{t_{s}^{0} }}} \right\}^{2} + \left\{ {\frac{{t_{t} }}{{t_{t}^{0} }}} \right\}^{2} = 1$$
(1)

Here \(t_{n}\), \(t_{s}\)\(t_{t}\) are the values of tensile or shear stresses which are necessary for the failure of the cohesive layer under pure tensile load or pure shear load. The symbol \(\langle\rangle\) represents the Macaulay bracket. It is used to describe that compressive stresses do not cause damage. The relative displacement between the top and the bottom of the cohesive layer is described by the components \(\delta_{n} ,\delta_{s}\) and \(\delta_{t} .\) The relationship between the stresses \(t_{i}\) and separations \(\delta_{i}\) (\(i = n,s,t)\) for each failure mode can be expressed as follows.

$$t_{i} = K_{i} \delta_{i}$$
(2)

where \(K_{i}\) (\(i = n,s,t)\) defines the stiffness of the interface for each failure mode.

Once failure has occurred, damage evolution begins. The damage is described using the variable \(D\). Once the criterion of Eq. (1) has been reached, the cohesion stiffness \(K\) decreases. The damage variable D now increases until it reaches the value \(D = 1\) for a completely fractured interface \(d = 1\). In case of a linear softening process the damage variable \(d\) can be expressed by the maximum value of mixed mode displacement \(\delta_{m }^{\hbox{max} }\) and the total mixed mode displacement \(\delta_{m}\).

$$D = \frac{{\delta_{m}^{f} \left( {\delta_{m }^{\hbox{max} } - \delta_{m}^{0} } \right)}}{{\delta_{m}^{\hbox{max} } \left( {\delta_{m}^{f} - \delta_{m}^{0} } \right)}},$$
(3)

The total mixed mode displacement \(\delta_{m}\) is calculated by Eq. (4).

$$\delta_{m} = \sqrt {\delta_{n}^{2} + \delta_{s}^{2} + \delta_{t}^{2} }$$
(4)

The effect of the damage variable \(D\) on the contact stresses is shown in Eqs. (5)–(7).

$$t_{n} = \left\{ {\begin{array}{*{20}c} {\left( {1 - D} \right)\bar{t}_{n} , \quad \bar{t}_{n} \ge 0} \\ {\bar{t}_{n} } \\ \end{array} } \right.$$
(5)
$$t_{s} = \left( {1 - D} \right)\bar{t}_{s}$$
(6)
$$t_{t} = \left( {1 - D} \right)\bar{t}_{t}$$
(7)

The contact stresses \(\bar{t}_{n}\), \(\bar{t}_{s}\) and \(\bar{t}_{t}\) are the stress components predicted by the traction separation approach for the current undamaged state of the interface.

The damage evolution is described using an energy criterion. The proposed approach of Benzeggagh and Kenane [17] is particularly well suited for the damage evolution in the field of epoxy and PEEK composites, which has already been shown in investigations by Camanho [16]. In Eq. (8), \(G_{\text{c}}\) describes the critical fracture energy for mixed mode fracture. The fracture toughness for each single mode is identified by \(G_{\text{Ic}} ,G_{\text{IIc}}\) and \(G_{\text{IIIc}}\). The exponent \(\eta\) describes the relationship between the single failure modes and is typically determined in a mixed mode bending test. According to [16], it is selected to 1.45.

$$G_{\text{c}} = G_{\text{Ic}} + \left( {G_{\text{IIc}} - G_{\text{Ic}} } \right)\left( {\frac{{G_{S} }}{{G_{T} }}} \right)^{\eta }$$
(8)

where

$$G_{S} = G_{\text{IIc}} + G_{\text{IIIc}}$$
(9)

and

$$G_{T} = G_{\text{Ic}} + G_{S}$$
(10)

Parameter Identification

To determine the critical energy release rate, various approaches such as the modified beam theory or the Compliance Calibration Method [18] are used in the literature. Common to all of them is the need for experimentally determined force–displacement curves of the composite and the optically recorded crack propagation during the tests.

Sener et al. [19] showed that the critical energy release rate can be determined in a wedge test by considering the peeled joining partner as a beam clamped on one side and subjected to a point load. The crack openings \(\delta\) and crack lengths \(l\) measured in the wedge tests together with the stiffness EI of the CFRP sheet metal result in the elastic work \(U\) stored in the beam according to [20].

$$U = \frac{{3{\text{EI}} + \delta^{2} }}{{2l^{2} }}$$
(11)

Thus, the energy stored in the CFRP sheet increases with increasing deflection. With further crack propagation, this energy is again reduced. This can be described by the critical energy release rate, which can be determined according to [21] as follows

$$G_{c} = - \frac{1}{b}\frac{dU}{{2l^{3} }} = \frac{{9{\text{EI}}h^{2} }}{{2bl^{4} }}$$
(12)

With the material properties from Table 1, the width \(b\) of the sample the crack openings and crack lengths measured in the test at different times of crack propagation, the critical energy release rate over the progressive crack length results as follows.

Table 1 Material properties of Aluminum and PEEK used for the model
Full size table

Due to the optical measuring method, it is only possible to quantify the deflection of the CFRP sheet metal from a crack length of 10 mm. The crack opening is measured up to a crack length of 30 mm. In this range of crack propagation the critical energy release rate for mode I is calculated. In Fig. 5 it is shown that this fluctuates in the range of 1 N/mm up to 1.3 N/mm. This can be attributed to the inaccuracies in the measurement of crack opening and crack length (Table 2).

Fig. 5
figure 5

Critical energy release rate as a function of crack length

Full size image
Table 2 Material properties of CFRP used for the model
Full size table

According to [16] the initial stiffness was chosen \(K = 10^{6} \;{\text{N}}/{\text{mm}}^{3}\) for each failure mode. The critical energy release rate of 1.2 N/mm was chosen on the basis of the results from Fig. 5. In order to fully describe fracture mode I, the critical fracture stress must be determined.

Determining the fracture stress from this type of test method is difficult, so further fracture mechanical tests are necessary. Therefore, in most cases, these parameters are fitted so that they correspond to the test results [11] (Fig. 6).

Fig. 6
figure 6

Equivalent model for determining the vertical force

Full size image

To determine the fracture stress, the vertical force responsible for the peeling process as well as the deflection of the organic sheet is determined using the beam theory. In the simulation, a displacement is applied at the contact point of the wedge to the organic sheet. The failure stress was then adjusted so that the measured reaction force at the contact point of the wedge in the simulation corresponds to the previously calculated forces from the experiment (Fig. 7).

Fig. 7
figure 7

Calculated vertical force from experiments/vertical force from simulation

Full size image

Afterward, the coefficients of friction of the contact pairings aluminum/steel or CFRP/steel were determined or adjusted using the measured reaction force on the wedge from the experiments and the simulation. The reaction force on the wedge was then compared with the experimental measurement results in the simulation. The comparison of the force–displacement curves is shown in Fig. 8.

Fig. 8
figure 8

Force–displacement curves: experiment/simulation

Full size image

Figure 8 shows clearly that the measured force up to the failure occurrence in the experimentally determined curve rises at a slightly flatter rate than the calculated curve from the simulation. This can be explained by the settlement behavior of the machine and the test specimens. The maximum force is also slightly higher in the experimentally determined curves than in the calculated curves from the simulation. However, the damage evolution over the remaining fracture surface shows a very good agreement between experiment and simulation.

Figure 9 shows the comparison of the failure mechanism of simulation (b)) and experiment (a)). It can be seen, that both the deformation of the CFRP sheet by the wedge and the peeling process show good agreement.

Fig. 9
figure 9

Wedge test: a) experiment, b) simulation

Full size image

Summary

In order to describe the failure behavior of a hybrid composite of CFRP and aluminum under quasi-static load, the finite element method was used. We introduced a surface-based cohesive zone model with a bilinear traction–separation approach. For the cohesive zone model, the critical energy release rate for fracture mode I was identified using quasi-static investigations on modified wedge test specimens. The approach of [21] was used for this purpose. Furthermore, the critical fracture stress for mode I was adjusted so that the results of the experiments and simulation showed good agreement. In summary, it can be said that it is possible to determine the critical energy release rate for fracture mode I of the hybrid composite analyzed here using the wedge test. By adjusting the breaking stress in the normal direction, the experimental results can be well reproduced. This becomes clear by comparing the failure progress of experiment and simulation. In the case of damage initiation, however, there are some differences which can be explained by a non-ideal positioning of the wedge in the experiment. Due to the previous assumptions of the fracture mechanical parameters for fracture modes II and III, these must be determined in further experiments.