Introduction

The arc root characteristics and the temperature distribution within the plasma core are a widely investigated topic in the field of plasma technology. The knowledge of arc root characteristics such as spot diameter, reattachment frequency and attachment dwell time may not only help to design an efficient plasma system for maximum heat transmission but also helps to devise methods to suppress the rate of electrode erosion. The fluctuations (and/or oscillations) of the arc strongly affect the thermal characteristics of the plasma plume inside the torch and the dynamic flow behavior of the jet outside the torch. The accurate determination of plasma temperature distribution is important for optimizing the processes such as of plasma chemical synthesis (Ref 1), plasma coating (Ref 2) or plasma in-flight treatment (Ref 3) since undesired thermal distribution due to arc fluctuations could have detrimental effects on the product quality and yield (Ref 4). Consequently, the investigation of arc fluctuation has been the subject matter of several research articles and monographs for the last three decades (Ref 5,6,7,8).

A well-known approach to produce a stable plasma is the “magnet-induced arc stabilization.” In this technique, a concentric magnet ring or a magnetic cylinder or a solenoid is fixed around the outer surface of the anode nozzle which has sufficient field strength to overcome the arc behavior due to the inherent convective and self-induced electromagnetic forces on the arc column (Ref 9). This method of arc stabilization requires a critical magnetic field strength to suppress the random (or oscillatory) arc behavior and induce a desired arc rotation within the arc chamber.

Several experimental investigations have been made to explore the arc dynamics inside the magnetically stabilized plasma torches, either by measuring the arc voltage fluctuations or by imaging techniques (Ref 8,9,10,11). The common observation made in all such reports is that the arc swirls in the azimuthal direction at a fixed velocity which aid in suppression of its oscillatory behavior. The angular velocity increases with as the magnetic field strength rises while the voltage fluctuations are reduced. Hu et al. reported that the electric arc forms a spiral shape while rotating under the influence of external magnetic field (Ref 8). Szente et al. have provided a simple correlation between arc rotational velocities (and frequency) with the magnetic field by balancing both the drag and magnetic forces (Ref 11). Their correlation shows that the velocity is proportional to \({B}^{0.6}\), which had been validated by several experimental measurements.

The high-speed rotation of the arc and arc root under an external magnetic field tends to reduce the arc constriction and results in a “diffused attachment” (Ref 12, 13). This observation was intriguing and counter intuitive given the fact that acceleration of charged particles under a strong Lorentz force resulting from the external magnetic field could potentially consolidate the charged particle to facilitate arc constriction. While reporting the formation of diffused arc, Li et al. suggested that the transformation of the arc from constricted to diffuse mode is due to the weakened skin friction of the arc root (Ref 12). Diffused behavior was also observed in the work of Wang et al. (Ref 14), particularly at high inlet gas flow rates. Although, at low gas flow rate, they reported the formation of a constricted arc. In majority of the experimental works, time-dependent voltage-drop fluctuations have been measured as a surrogate parameter to analyze the arc fluctuation and arc length inside the torch. This type of analysis is preferred over imaging technology as it is difficult to distinguish the arc from the highly illuminating plume. Even by using a narrow bandwidth filters, the imaging of the longitudinal section of arc is challenging and in the majority of cases one could only visualize the radial section of the electric arc near the exit (Ref 9, 13). While some innovative approach has been undertaken to capture the dynamic arc image inside the anode, for example the work of Ghorui et al. using partially reflecting mirrors (Ref 15, 16), the image does not capture the entire length of the electrode and limited for electrodes with large bore diameter (Ref 16). In a separate work, Ghorui et.al. (Ref 15) also attempted to determine the anode arc attachment position by dissecting the anode into 3 longitudinal sections along the azimuthal direction, such that each section cover’s 1/3 of the total circumference. All the 3 sections were separated by a thin insulator. They independently measured the current in each section which helped to determine the approximate arc attachment location. They reported “diffuse connection” for a wider anode bore diameter at high arc currents and lower gas flow rated. While a useful technique, it can only help to narrow down the identification of the arc attachment location to 1/3rd part of the anode circumference. This technique cannot accurately inform about the attachment spot and attachment size for a constricted attachment due to the limited number of azimuthal sections in the anode. The complex nature of arc behavior and the high cost of designing experimental program often hinders detailed investigations of the arc root behaviors under a variety of scenarios. Fortunately, the advancements in computation can assist to fill the knowledge gap with a help of a comprehensive modeling technique.

Several 2D and 3D steady-state models to study arc behavior have been reported. For example, Li et al. developed a 2D fluid model to study the “diffused” arc mode by assuming an axisymmetric nature of the arc (Ref 12). They observed that the arc structure is constricted in the axial direction while it expands (diffuses) in the radial direction. Similarly, Park et al. developed a three-dimensional fluid model to study the effect of operating conditions on the plasma torch with arc stabilization achieved using external magnetic field; however, in contrast to the findings reported in the experimental works, this study did not report a “diffused” arc attachment (Ref 17). However, Baeva et al. conducted a comprehensive two temperature 3D modeling and validated the experimentally observed dispersed arc behavior (Ref 18).

The majority of the previous works accepts that the dynamics of arc behavior is the consequence of the drag force and magnetic force; however, there is no detailed investigation reported on the transient arc behavior under an external magnetic field. Studying a transient system under varying external field strength helps to capture the dynamic changes of the system which provides detailed insights into the phenomenological behaviors and potentially shed light on the nature of arc constriction. Here, we report our investigation on the dynamic arc behavior under the influence of external magnetic field using a transient 3D modeling approach. We also report our finding on arc characteristics under the influence of various operating conditions such as gas flow rates, arc current and external magnetic field strength.

Mathematical Model

Geometry Description

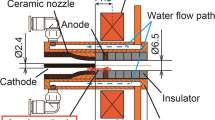
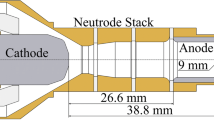
The cross-sectional view shown in Fig. 1 describes the plasma torch geometry. The computational domain includes the plasma gas chamber (i.e., the space between the inner surface of the hollow anode and the surface of solid cylindrical cathode). The gas enters through the ‘inlet,’ and the plasma jet exits from the ‘outlet’ section of the computational domain. The length and internal diameter of the plasma arc chamber are 80 mm and 10 mm, respectively. The cathode protrudes 10 mm into the simulation domain, while remaining length of the cathode which is upstream of the gas inlet is outside the scope of simulation geometry. The cathode diameter is 1.8 mm. The model geometry only includes the plasma gas chamber and is bounded by the walls of the cathode and anode. The anode and cathode material (solid metal body) are outside the scope of this simulation.

Fig. 1
figure 1

Sectional view of plasma torch for the present study, the full 3D body of the torch is generated by rotating the sectional geometry about the central axis (not to scale). 5 boundaries (inlet, cathode surface, anode surface, cathode tip and outlet are shown)

Full size image

Assumptions and Governing Equations

The following assumptions are used to develop a 3D transient plasma torch model (Ref 19,20,21).

  • 1. Plasma gas is argon.

  • 2. Plasma is in LTE (local thermodynamic equilibrium).

  • 3. Plasma flow is optically thin, turbulent and weekly compressible.

  • 4. Gravitational and viscous dissipation effects are not considered.

  • 5. Plasma is assumed to have Newtonian behavior.

As the modeling is restricted to the local thermodynamic equilibrium (LTE) assumption, the model outcome is compared with an experimental system reported in the literature which suggests that the LTE assumption is valid at high operating currents, similar to that used in the model. The present model with LTE assumption is also appropriate when using low gas flow rates (less than 18 slpm) and a smaller diameter of anode nozzle (10 mm). Last but not the least, magnet-induced high-speed rotation of the electric arc inside the torch ensures the constant and uniform heating of inlet gas, which reduces the thickness of the non-equilibrium zone in the present context.

The governing equations for simulating the transient behavior of the arc inside the plasma torch are as follows (Ref 22).

Conservation of mass:

$$\frac{\partial\uprho }{\partial \mathrm{t}}+\nabla \cdot \left(\rho \mathbf{v}\right)=0$$
(1)

Conservation of mass-averaged momentum:

$$\frac{{\partial \left( {\rho \overrightarrow {{\mathbf{v}}} } \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {\mathbf{v}} \otimes {\mathbf{v}}} \right) = \user2{J}~ \times {\mathbf{B}} - {\text{~}}\nabla p + ~\nabla \cdot \overleftrightarrow {\boldsymbol{\tau} }$$
(2)

Conservation of energy:

$$\frac{\partial (\rho h)}{\partial t}+\nabla \cdot \left(\rho \mathbf{v}h\right)={\varvec{J}} \cdot \left({\varvec{E}}+\mathbf{v}\times {\varvec{B}}\right)- \dot{R}+ \nabla \cdot \left(\kappa \nabla T\right)+ \frac{5}{2}\frac{{k}_{\mathrm{B}}}{e}{\varvec{J}}\cdot \nabla T+ \frac{\partial p}{\partial t}$$
(3)

where \(\rho\) and \(h\) are the density and specific enthalpy of argon plasma, respectively. \(\mathbf{v}\) is the plasma velocity field, T is plasma temperature, p is plasma pressure, \(\overleftrightarrow {\boldsymbol{\tau} }\) is shear stress, \(\kappa\) is thermal conductivity, \({\varvec{B}}\) is the magnetic field, \({\varvec{J}}\) is electric current density and \({\varvec{E}}\) is the electric field inside the plasma, calculated by \({\varvec{E}}= -\nabla \phi\). The term \(\dot{\mathrm{R}}\) represents the radiation losses, which is obtained from the net emission coefficient of argon plasma which is a function of temperature (Ref 23).

The term \(\frac{5}{2}\frac{{k}_{\mathrm{B}}}{e}{\varvec{J}}\cdot \nabla T\) is called electron enthalpy flux which is an important heat transfer mechanism at the cathode tip, the anode surface and in the arc fringes. While the inclusion of this term in the balance equation may slightly overestimate the heat flux, mainly near the zones that are not truly at exact LTE conditions; however, this factor strongly influences the heat transfer mechanism in the specific location such as portion of cathode tip, the anode surface and in the electric arc fringes (Ref 24) which is more important for this study as it captures the underlying physical phenomenon in the arc.

The \({k}_{\mathrm{B}}\) in Eq. 3 indicates the Boltzmann constant, and \(e\) represents the electron charge.

The viscous stress tensor \(\overleftrightarrow {\boldsymbol{\tau} }\) for Newtonian fluid is given by

$$\overleftrightarrow {\boldsymbol{\tau} } = ~\mu \left( {\nabla {\mathbf{v}} + ~\left( {\nabla {\mathbf{v}}} \right)^{t} - \frac{2}{3}\left( {\nabla \cdot {\mathbf{v}}} \right)\overleftrightarrow {\mathbf{I}}} \right)$$
(4)

where \(\mu\) represents the effective dynamic viscosity, which is the sum of laminar viscosity and turbulent viscosity, superscript t represents the transpose operator, and \(\frac{2}{3}\left( {\nabla \cdot {\mathbf{v}}} \right)\overleftrightarrow {\mathbf{I}}\) indicates the fluid dilation term arising from Stoke’s hypothesis for the dilatational viscosity. The laminar viscosity is assumed to be a function of plasma temperature. The turbulent viscosity is obtained from the following expression.

$${\mu }_{\mathrm{t}}= \rho {C}_{\mu }\frac{{k}^{2}}{\epsilon }$$
(5)

where \({C}_{\mu }\) is the coefficient of turbulent viscosity, k is turbulent kinetic energy and \(\epsilon\) is turbulent dissipation rate. Turbulent kinetic energy and dissipation rate are obtained by solving separate conservation equations for both of these variables. A two-equation realizable k–\(\epsilon\) model is used, and the conservation equations for the realizable k–\(\epsilon\) model are presented below

$$\frac{\partial \left(\rho k\right)}{\partial t}+\nabla \cdot \left(\rho \mathbf{v}k\right)=\nabla \cdot \left(\left(\mu + \frac{{\mu }_{\mathrm{t}}}{{\sigma }_{k}}\right)\nabla k\right)+{P}_{k}+{P}_{\mathrm{b}}-\rho \epsilon -{Y}_{\mathrm{M}}+{S}_{k}$$
(6)
$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\nabla \cdot \left(\rho \mathbf{v}\upepsilon \right)=\nabla \cdot \left(\left(\mu + \frac{{\mu }_{\mathrm{t}}}{{\sigma }_{\upepsilon }}\right)\nabla\upepsilon \right)+\rho {C}_{1}S\upepsilon -\rho {C}_{2}\frac{{\epsilon }^{2}}{k+\sqrt{\upsilon \epsilon }}+{C}_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{P}_{\mathrm{b}}+{S}_{\upepsilon }$$
(7)

The definition of the variables is provided in the nomenclature. More information about the calculation of these parameters is presented in Ref 25.

Electric current inside the plasma is determined from the current continuity equation along with Ohm’s law. The simplified form of this equation is presented in the electric potential formulation.

$$\nabla \cdot ({\varvec{J}})=\nabla \cdot \left(\sigma (\nabla \phi -\mathbf{v} \times {\varvec{B}}\right))= 0$$
(8)

where \(\phi\) is electric potential, \(\mathbf{v}\) is averaged plasma velocity and \(\sigma\) is electrical conductivity which is a function of plasma temperature. \({\varvec{B}}\) is the total magnetic field experienced in the plasma, which is the sum of self-induced magnetic field \(\left({{\varvec{B}}}_{\mathrm{s}}\right)\) and external magnetic field \(\left({{\varvec{B}}}_{\mathrm{e}}\right)\). Electric current density is computed from\({\varvec{J}}= -\sigma (\nabla \phi -\mathbf{v}\times {\varvec{B}})\). The term \(\sigma (\mathbf{v}\times {\varvec{B}})\) contributes to the current density due to the current flow through the magnetic field \({\varvec{B}}\) by combining the minimal influence of hall-effect and electron pressure. More information on this formulation of the electric current density is found in Ref 26.

The self-induced magnetic field is formed around the electric current inside the plasma environment. This magnetic field is calculated from \({{\varvec{B}}}_{\mathrm{s}} = \nabla \times {\varvec{A}}\), where \({\varvec{A}}\) is determined from Ampere’s law as follows:

$${\nabla }^{2}{\varvec{A}}= - {\mu }_{0}{\varvec{J}}$$
(9)

where \({\mu }_{0}\) = \(4\pi \times {10}^{-7}\) Tm \({\mathrm{A}}^{-1}\).

The thermodynamic and transport properties of argon plasma gas are taken from the literature (Ref 27). The OpenFOAM CFD fluid code (generally used for compressible flows, called rhoPimpleFoam) was modified to include the additional terms [Lorentz force (\({\varvec{J}} \times {\varvec{B}})\), joule heating \(({\varvec{J}} \cdot \left({\varvec{E}}+\mathbf{v}\times {\varvec{B}}\right)\) and electron enthalpy flux (\(\frac{5}{2}\frac{{k}_{\mathrm{B}}}{e}{\varvec{J}}\cdot \nabla T\))] in the momentum and energy equations together with electromagnetic relations described above. Due to high heat conductivity of the anode material (typically made from zero oxygen copper), the temperature gradient across the anode material is small and hence, the metal body has been excluded from the simulation for simplicity and a heat flux boundary condition is used. The gas boundary layer on the inner surface of the anode provides major thermal resistance.

Boundary Conditions

The governing equations shown in the previous section are solved with appropriate boundary conditions to simulate the plasma arc inside the torch. Figure 2 shows the meshing of the geometry of interest.

Fig. 2
figure 2

Geometry and meshing of plasma torch model used in the present study

Full size image

The computational domain boundaries are divided into five different parts to specify the boundary conditions. These boundaries are inlet, outlet, cathode surface, cathode tip and anode surface. The boundary conditions at these places are presented in Table 1.

Table 1 Boundary conditions
Full size table

The inlet gas flow into the plasma torch through the space between the anode wall and cathode surface has an annular flow profile which has been imposed as inlet velocity \({\mathbf{v}}_{i}\) condition.

The inlet temperature is set to an arbitrary temperature of 500 K, although it mimics a preheated incoming gas. The plasma exits into an ambient atmosphere having a pressure of 1 bar. A no-slip boundary condition is imposed at the electrode surfaces (cathode tip, cathode surface and anode). This boundary condition is specified to have smooth continuity of pressure at the plasma-electrode interface. The temperature of the cathode tip is set to 3500 K, which is selected to be slightly lower than the melting point of tungsten metal. The cathode’s cylindrical surface is considered to be thermally insulated and therefore, has zero heat flux through this boundary.

A convective heat transfer boundary condition is used for the anode wall. The equation for heat flux through the anode boundary is presented below.

$${q}_{\mathrm{W}}= {h}_{\mathrm{w}}\left({T}_{\mathrm{wall}}-{T}_{\mathrm{water}}\right)$$
(10)

where \({q}_{\mathrm{W}}\) is heat transfer from the plasma through the anode boundary. \({h}_{\mathrm{conv}}\) represents the convective heat transfer coefficient which is equal to \({10}^{5} \mathrm{W}/({\mathrm{m}}^{2} \mathrm{K})\) [approximates the convective heat transfer due to turbulent flow in a pipe (Ref 28)]. \({T}_{\mathrm{wall}}\) and \({T}_{\mathrm{water}}\) are anode inner wall temperature and cold-water temperature, respectively. The effects of the sheath in the present model are incorporated by using the LTE-diffusion approach which is proposed by Lowke and Tanaka (Ref 29). This approach requires that the size of the neighboring cell next to the cathode surface and anode surface in the order of electron diffusion length, which is approximately 0.1 mm.

The normal electric potential is specified as \(-\frac{\left|{{\varvec{J}}}_{\mathbf{c}\mathbf{a}\mathbf{t}\mathbf{h}}\right|}{\sigma }\), where \({|{\varvec{J}}}_{\mathbf{c}\mathbf{a}\mathbf{t}\mathbf{h}}|\) is the magnitude of current density. The uniform profile of electric current density is specified over the cathode tip surface. A zero electric potential is imposed over the anode surface to allow the flow of current through it. At the remaining boundaries, the normal derivative of electric potential is maintained at zero to ensure no loss of electric current through them.

The normal derivative of the magnetic potential is set to zero for all boundaries except at the outlet where the magnetic vector potential is zero (0 0 0) since the magnetic vector potential vanishes far away from the outlet (Ref 22, 28, 30). The zero-flux condition is valid in present case given the fact that the dominance of external magnetic field nullifies the influence of relatively weaker self-induced magnetic field on overall arc behavior (Ref 31, 32).

Model Geometry and Meshing

The plasma torch geometry is divided into 689,472 hexahedron cells. The meshing is carried out using ANSYS work bench software, and the meshing is presented in Fig. 2. The number of cells in azimuthal direction (\({n}_{\theta }\)) is 64. The radial and axial cell sizes (\(\Delta S\)) are equal and set to 0.2 mm. The size of anode boundary face in azimuthal direction (\({\Delta S}_{\theta }\)) is 0.49 mm.

To test the mesh independence, few simulations were carried out with two additional mesh sizes (a finer and a coarser mesh) whose details are; (1) N = 1 534,743 (\({n}_{\theta }=84 , \Delta S=0.15\,\mathrm{ mm}\) & \({\Delta S}_{\theta }\) = 0.37 mm) and (2) 212,553 \(({n}_{\theta }=44 , \Delta S=0.3\,\mathrm{ mm }\&\) \({\Delta S}_{\theta }\)= 0.71 mm), respectively. The corresponding mesh dependency study is included in SI-I.

Numerical Methods

All the governing equations are discretized in the Cartesian coordinates system by a finite volume method. Time-dependent terms in the governing equations are discretized using Runge–Kutta first-order method. Other functions such as gradient, divergence and Laplacian terms are discretized by using Gauss linear method. The SIMPLE algorithm including pressure correction is used along with a momentum interpolation for iterative computations at every time step. The overall time steps during the simulation are varied between 0.01  and 0.05 \(\mu s\). The time steps are controlled by conventional CFL condition which is defined as

$${C}_{0}= \frac{{\mathrm{v}}_{x}\Delta t}{\Delta x}+ \frac{{\mathrm{v}}_{y}\Delta t}{\Delta y}+\frac{{\mathrm{v}}_{z}\Delta t}{\Delta z} \le 1$$
(11)

The CFL number \({C}_{0}\) is maintained at 0.1.

Model Equation Validation

The correctness of the model equations (MHD formulations) and the accuracy of CFD codes as well as the associated numerical technique are validated by applying the above model equation on a transferred plasma torch geometry which is similar to those used in the experimental work of Hsu et al. (Ref 33) and comparing the results with the published experimental results. The operating arc current is 200A, and the distance between the cathode tip and the anode surface is maintained at 10 mm. The cell size thickness near the cathode and anode boundary is 0.1 mm. The model validation and the results for the transferred arc are shown in supporting information SI-II. The temperature distribution predicted by the present model has good agreement with the experimental results.

Modeling Results and Discussion

Operating Conditions and Arc Ignition

Several simulations were carried out by changing the external magnetic field strengths, arc currents and inlet gas flow rates to explore the arc behavior under different operating conditions. The magnetic field strength was varied between 0 and 0.3 T, arc current ranging between 200 and 300A and the inlet gas flow rates varying from 18 to 73 slpm.

The arc ignition was simulated by momentarily imposing a single electrical micro-pulse. This was achieved by adding a high-electrical conductivity circular disk in the model with a thickness of 0.1 mm (equivalent to 1 cell) at a pre-specified position on the anode as per the method described by Trelles et al. (Ref 28) The radial profile of the conductivity disk is given below.

$${\sigma }_{\mathrm{b}}={\sigma }_{\mathrm{b}0}\mathrm{exp}(-{\beta }_{\mathrm{b}}{\left({r}_{\mathrm{b}}/{R}_{\mathrm{b}}\right)}^{{n}_{\mathrm{b}}})$$
(12)

where \({r}_{\mathrm{b}}\) is the radius. Values of parameters used in the present study are \({R}_{\mathrm{b}}=0.5\, \mathrm{mm}\), \({\beta }_{\mathrm{b}}=6\), \({n}_{\mathrm{b}}\) = 4 and \({ \sigma }_{\mathrm{b}0}= {10}^{4}\, \mathrm{S}\, {\mathrm{m}}^{-1}\). The axial position of the high electrical conductivity disk is 3.5 mm from the inlet. The arc attachment position on the circumference of the highly conductive disk is arbitrarily chosen and fixed at zero degrees from the axial plane. The residence time of the micro-pulse is 1 s\(\mu\). Increasing this time and/or electrical conductivity of the disk does not affect the final results but simply increases the time for dissipation of this initial effect. A temperature of 5000 K was imposed on all the cells as the initial condition. Hereon, we take the liberty to use the terms Plasma and Plasma gas interchangeably. Although in the strict sense, the plasma differs from the actual gaseous behavior, using the term plasma gas helps to conceptualize that the plasma flow has gas-like behavior.

Flow and Electric Fields Inside the Plasma Torch

Figure 3(a), (b), and (c), respectively, shows profile of three properties ((instantaneous electric current density, temperature and absolute pressure) of the plasma inside the torch at 1.09 ms under the influence of external magnetic field strength of 0.12 T. An arc column is generated between the cathode tip and the anode, wherein the cathode attachment is fixed while the arc attachment at the anode surface rotates due to the externally imposed Lorentz force. The distribution of electric current density is shown in Fig. 3(a), which is the product of the electrical conductivity and electric field obtained from the solution of the electric potential equation. The axial location of anode arc attachment is approximately 6.3 mm from the cathode tip, and the maximum current density at this location is approximately 24 A/mm2.

Fig. 3
figure 3

Electric current density (a), temperature (b), absolute pressure(c) and velocity magnitude(d) inside the plasma torch (I = 200A and Q = 54 slpm)

Full size image

The heat and momentum transfer due to high-speed arc rotation causes the plasma gas to swirl at different rates, as evidenced by the helical temperature profile in Fig. 3(b). The swirl intensity decreases as the plasma gas moves downstream and away from the arc zone. The plasma temperature has a maximum value of 21,900 K near the cathode tip; however, the high temperature zone gets diverted away from the axial centerline as the plume moves downstream from the cathode tip. The profile of absolute pressure shown in Fig. 3(c) confirms the helical path taken by the plasma gas as it swirls inside the chamber. The plasma gas swirl creates a low-pressure zone along the centerline of the plasma torch. This pressure depression causes a small backflow of the downstream cold plasma gas which creates a cold boundary interface in the inner region of the arc.

Figure 3(d) presents the sectional view of the radial distribution of velocity at six different axial locations. The first snapshot shows the radial velocity at X = 11 mm from the torch entrance (which is nearly 1 mm distance from the cathode tip in downstream direction). Maximal velocity is observed close to the cathode tip due to two primary factors; (1) Gas expansion due to joule heating and (2) acceleration caused by Lorentz force. The latter one is also called magnetic constriction or magnetic pinching effect (Ref 34).

As the incoming cold gas from the inlet passes through the arc zone, the induced shear due to the swirling causes the plasma gas to rotate inside the plasma torch. A sectional view of axial velocity at X = 13–17 mm clearly shows the rotational flow near the anode wall. Subsequently, it develops a low-pressure region at the center of the torch along the central axis as seen in Fig. 3(c).

Figure 4 shows the snapshot of current density distribution in a radial cross section of plasma torch at various time-steps with an interval of 0.02 ms. The cross sections at different time steps are not taken at a fixed axial position; instead, the sectional slice is taken at the axial position where the maximum current density is observed for that given time step. This indicates that the arc attachment on the anode surface not only rotates around the anode circumference but also moves axially. Although the axial position of anode arc attachment only deviates by a maximum of 0.02 mm over the entire rotation and the average position is at X = 16.3 mm. The arc can be seen to rotate in the clockwise direction due to the application of a positive axial magnetic field, while the rotational frequency is around 10.6 kHz.

Fig. 4
figure 4

Snapshots of electric current distribution inside the plasma torch. The cross section is taken at the axial location where the arc attaches to the anode

Full size image

Since the snapshot of radial cross sections is taken at the axial location of approximately X = 16.3 mm, the cathode attachment is not seen in the image. The anode attachment is semi-constricted with a faint diffuse tail following it.

Phenomenological Behavior of Transient Arc Under Axial Magnetic Field

The transient behavior of the arc under the influence of an externally imposed axial magnetic field is a complex feature due to the involvement of multiple forces such as (1) drag force on the arc column due to the incoming gas flow, (2) frictional resistance on the arc root at the electrode boundary and (3) the electromagnetic force on the arc column due the imposed magnetic field acting on it. Additionally, when an electric arc is “curved,” two additional phenomena get manifested within the plasma system. The first is the self-induced Lorentz force in the curved region of the arc that acts to increase the “curvature” of the arc (Ref 19), while the second phenomenon arises due to temperature inhomogeneity in the region of the curved arc that has a nonzero relative velocity with respect to the adjacent cold gas (Ref 35). Due to this, the arc (or the column of high temperature) apparently experiences an additional force in the direction which is opposite to the Lorentz force due to the external magnetic field, which determines the dynamic behavior of the arc.

In our earlier work on a plasma torch with straight gas injection and without imposing any external magnetic field (Ref 19), we have shown that the arc-root on the anode is pushed downstream due to the drag force of the incoming gas and achieves a stable attachment position where the drag force and self-induces Lorentz forces attempt to balance each other. The major portion of the arc column in such a system is along the axial centerline due to the strong effect of the cathode jet, while the tail-end of the arc bends and attach to the anode (Ref 19). The arc is also constricted radially due to the pinch effect arising from self-induced Lorentz force. In the present work, however, under the influence of an externally imposed axial magnetic field, it can be seen that the arc column tends to expand in the azimuthal direction and gets off-centered almost immediately downstream of the cathode tip. Due to this shift, the anode attachment moves to an upstream location relative to an arc in a plasma torch without any external magnetic field.

In order to understand the dynamic transformation of the arc structure without and with the external magnetic field, we conducted a transient simulation while dynamically changing the external axial magnetic field strength. The operating arc current is set to 200A, and the gas flow rate is fixed at 37 slpm. Initially, the plasma is generated without any external magnetic field and the system is allowed to stabilize until t = 2 ms, following which an external magnetic field is imposed which increases linearly from zero to 0.18 T at a rate of 0.9 T/ms and achieves the maximum value at 2.2 ms. After this point of time, a constant magnetic field is maintained at 0.18 T.

The corresponding axial and radial distributions of current density are displayed in Fig. 5. In the absence of an external magnetic field, the arc does not rotate and instead the anode arc root undergoes a periodic fluctuation with the attachment, detachment and re-attachment on the diametrically opposite surface of the anode wall. This kind of motion has been investigated and discussed in our previous work (Ref 19) and also other works (Ref 28, 30). Figure 5(a) (left) shows the distribution of electric current density along the length of the plasma torch at t = 2 ms. At this stage, the arc tail seems to fluctuate by reattaching alternatively between point A and point B on the anode surface. The maximum current density is nearly 6.6 A/mm2 at the anode surface, and the attachment is at an axial location of approximately X = 25.5 mm from the torch inlet. The radial cross-sectional distribution of current density at X = 25.5 mm is shown in the right-hand side image. Both the axial and radial current density profiles in Fig. 5(a) (left and right) show that the arc attachment on anode wall is constricted in the azimuthal as well as in the axial directions. The formation of new attachment (B) is presented in Fig. 5(b). Beyond t = 2.08 ms, the effects of the imposed magnetic field are manifested in the arc behavior. The axial magnetic field influences the radial part of the arc column to move azimuthally due to the induced Lorentz force. This movement does not directly impact the axial length of the arc column, but the heat mixing due to azimuthal movement changes the thermodynamics and transport properties due to conductive and convective heat transfer mechanisms, which affects the fluid conductivity. Eventually, both axial and azimuthal motion causes the arc column to form a spiral. A spiral shape of the arc column has been reported in the literature (Ref 36). This process ultimately spreads out the charged species in the azimuthal direction causing the azimuthal expansion of the arc attachment as seen from Fig. 5(c) (right) and consequently lowering the electrical conductivity and the maximum temperature at the arc attachment due to the LTE assumptions.

Fig. 5
figure 5

The time snapshot of axial (left) and radial (right) electric current density distribution inside the plasma torch; (a) t = 2 ms, (b) t = 2.04 ms, (c) t = 2.08 ms, (d) t = 2.12 ms, (e) t = 2.16 ms and (f) t = 2.2 ms

Full size image

The commencement of arc rotation is seen from the position of red line of axis in Fig. 5(d) (right). (Color image only shown in online version). The rotational motion of the arc causes the cold gas adjacent to the arc to also rotate due to the combined viscous-shear effect and strong temperature gradients, which consequently reduces the downstream axial velocity of the plasma gas. The lowering of downstream axial velocity reduces the convective drag force on the anode arc-root attachment which promotes the anode arc attachment to move upstream with increasing magnetic field strength.

By tracking the progression of arc attachment in the azimuthal direction between t = 2.04 ms and t = 2.16 ms, it is seen that the arc abruptly detaches and then, reattaches at the diametrically opposite surface, (Fig. 5(d)-right and (e)-right, respectively). While this is commonly observed in a torch operating without any forced arc rotation, it is manifested in the present case due to weaker influence of the external magnetic field at the given time steps. Nevertheless, despite abrupt reattachment, the simultaneous angular rotation of the anode arc attachment is apparent by examining the axis of attachment, together with axial movement of arc attachment at an upstream location.

In the subsequent time-steps, the external magnetic field strength increases linearly and consequently the arc length is lowered as the arc attachment moves further upstream. The major portion of the arc tends to curve in the azimuthal direction and at the same time the movement in the axial direction results in a formation of a helical structure. Though clear helical structure cannot be seen from the image shown in Fig. 5, earlier images in Fig. 3 corroborate the formation of the helical structure. Such arc formation has been reported in past (Ref 12, 18). As seen earlier (Fig. 3), the gas swirl causes a lower pressure along the central axis that causes reflux of cold gas along the central axis. The cold gas in the central portion of the torch pushes the arc further away from the central axis, as depicted in Fig. 5(d) (left).

At t = 2.2 ms and beyond, the arc structure maintains a steady behavior while rotating in the clockwise direction at a frequency of nearly 12 kHz as seen in Fig. 5(f).

The overall process indicates that while the arc-root tends to exhibit a constricted behavior, but it is followed by a diffuse tail, i.e., the arc is not fully constricted. Thus, it is improper to assume that the magnetic force will consolidate all the charged particles during rotation and result in a fully constricted arc. Another school of thought is that the experimentally observed diffused behavior of the magnet-induced rotating arc is an artifact of the dispersion of the heat due to convection (Ref 36) and the current flow is not necessarily diffused. Since our simulation is based on the LTE assumption, the results provided here can neither approve nor disprove this hypothesis and a non-LTE model may shed some light which is beyond the scope of this article.

Parametric Investigations

Effect of Magnetic Field Strength on Arc-Attachment Gap

A few sets of simulation were carried out to assess the effect of the external magnetic field on the arc length (i.e., stretching). To quantify the arc-stretching, an arc-attachment gap (Larc-gap) was computed, which is an axial distance between the cathode tip and anode attachment. The Larc-gap is important in sizing the anode nozzle in practical application. This arc-attachment gap (or arc-length) is distinguished from another parameter, “absolute arc-length” (total arc length which includes both radial curving and axial distance between the attachment on anode and cathodes), which includes the full segment of the arc that follows the helical pattern. The simple definition of arc length based on arc-attachment gap is done to have parity with experimental measurements since the arc-attachment gap can be conveniently measured by observing the location of electrode erosion in anodes.

Figure 6 shows that the arc attachment gap reduces with the increase in magnetic field strength. As discussed in previous section, the increase in the magnetic field strength amplifies the Lorentz force which accelerates the charged species in the azimuthal direction. Thus, intensifying the arc curvature and facilitating dispersion of the arc. Simultaneously, the rotational motion of the plasma gas reduces the downstream axial drag on the anode attachment, which promotes the arc attachment to an upstream location thus reducing Larc-gap.

Fig. 6
figure 6

Effect of magnetic field on the arc attachment gap (I = 200A and Q = 54 slpm)

Full size image

Effect of Magnetic Field Strength on Arc Potential and Rotational Frequency

The effect of magnetic field strength on the voltage-drop between cathode and anode as well as arc rotational frequency is shown in Fig. 7(a) and (b), respectively. Counter-intuitively, the arc potential tends to increase despite the decrease in the arc-gap as the magnetic field strength was raised (shown above). However, as described earlier ("Effect of Magnetic Field Strength on Arc-Attachment Gap" section), the arc-attachment gap is not a true indication of absolute arc length. The “absolute-arc length” would rather increases as the arc forms a helix type structure via the expansion in the radial and azimuthal direction due to increase in the field strength which corresponds to the rise in arc potential. Thus, the arc potential is a surrogate measurement for the change in absolute arc length. A similar trend of increase in arc potential as the magnetic field was raised was also reported by Saito et al. [10]. The average arc potential drop is approximately 23.25 V at 0.04 T (Fig. 7(a)).

Fig. 7
figure 7

Voltage-drop and arc rotational frequencies as a function of magnetic field strength (I = 200A and Q = 54 slpm)

Full size image

The increasing trend of arc rotational speed with magnetic field strength is seen in Fig. 7(b). The behavior of arc rotational frequency is in agreement with the previous experimental work by Szente et al. (Ref 10, 11). Their theory and model show that the arc rotational velocity is directly proportional to the \({{B}_{\mathrm{e}}}^{0.6}\). In the present study, the power-law fitting of the frequency data with magnetic field shows that it is proportional to the \({{B}_{\mathrm{e}}}^{0.64}\). The rotational arc dynamics for three different magnetic fields are further discussed in SI-III.

The time-averaged radial distributions of the temperature and velocity profiles at the exit of the plasma torch are examined at three different magnetic field strengths, and the results are shown in Fig. 8. The profiles are averaged over five complete arc rotations to ensure accuracy in the reported results. The average value of temperature and axial velocity was increased with the increase in the magnetic field strength. It further shows that the axial velocity profiles are not parabolic at a high rotational speed of arc when subjected to external magnetic field strength of Be = 0.12 T and higher. The existence of a substantial fluid swirl at the exit of the torch is the main factor behind the deviation from the parabolic profile.

Fig. 8
figure 8

Time-averaged axial velocity (a) and temperature distribution (b) at the exit of the plasma torch for three different magnetic field strengths (I = 200A and Q = 54 slpm)

Full size image

Effect of Arc Current and Gas Flow Rate on Arc Rotational Frequency and Arc Gap

Simulations were carried out with five different input currents; (1) 200A, (2) 225A, (3) 250A, (4) 275A and (5) 300A, all the while maintaining a constant magnetic field of 0.12 T. Figure 9(a) and (b) shows the effect of arc current on the frequency of arc rotation and length of arc column, respectively. As the magnetic force is responsible for arc rotation which is directly proportional to the magnetic field strength and the arc current, it is obvious to notice the increase in the arc rotational frequency as the current was raised, together with a decrease in the arc length (or arc attachment gap). The frequency of arc rotation seems to follow a curvilinear profile, as the rate of increase in the rotational frequency is high at lower level of arc current and flattens at higher arc current. This behavior is an outcome of change in the arc constriction with increase in arc current that influences the Lorentz force due to external magnetic field which is expressed as (\({J}_{\mathrm{r}}\times {B}_{x}\)).

Fig. 9
figure 9

Effect of arc current on the frequency of arc rotation (a) and length of arc column (b) for Be = 0.12 T

Full size image

As the arc current is increased, it increases the radical current (\({J}_{\mathrm{r}}\)) as well as the Lorentz force, which consequently increases the frequency. However, the increase in the arc’s rotational frequency also makes the arc more diffused due to the spread in the azimuthal direction and formation of the arc spiral, which reduces the arc radical current and consequently reducing the Lorentz force as well as rotational frequency. Eventually both the effects are balanced and the arc’s rotational frequency ceases to increase any further causing the curve to flatten.

The trend of rotational frequency is mimicked by the arc attachment gap length. The rotational arc dynamics for three different arc currents are further discussed in SI-IV.

Finally, Fig. 10(a) and (b) presents the effect of input gas flow rate on the frequency of arc rotation and length of arc column while maintaining a constant arc current of 200A and magnetic field of 0.12 T, respectively. The arc-attachment gap or the axial extension of arc column is strongly dependent on the gas drag force, and hence, the arc-attachment gap increases with the gas flow rate, while the rotational frequency reduces.

Fig. 10
figure 10

Effect of gas flow rate on the frequency of arc rotation (a) and length of arc column (b) for Be = 0.12 T

Full size image

Conclusions

In this article, we have investigated the effect of an external axial magnetic field on the arc dynamics inside a non-transferred DC plasma torch domain. The conclusions drawn from the present study are shown below.

  1. 1.

    The imposed axial magnetic field creates a strong Lorentz force on the arc column that swirls the arc. The swirling of the arc reduces the axial fluctuation of the arc column. The rotation of the arc causes the arc to form a helical structure as it extends in the radial and azimuthal directions while reducing its axial length. The results clearly shows the axial constriction of arc column and azimuthal expansion of arc column in the presence of the external magnetic field.

  2. 2.

    The variation of the magnetic field also impacts the attachment gap and voltage drop of the plasma torch. The arc attachment gap decreases as the magnetic field strength is raised, whereas the voltage-drop increases with magnetic field strength. The rise in the voltage drop at higher magnetic fields is attributed to the drop in the average arc column temperature under higher turbulence mixing between plasma and inlet cold gas.

  3. 3.

    The variation of inlet gas flow rate exhibited a significant impact on the arc rotational frequencies as well as arc attachment gap. The rotational frequencies are observed to decrease with the increase in the inlet gas flow rate, whereas the arc attachment gap increases strongly with rising in the gas flow rate.