Abstract
The properties of thermally sprayed coatings depend heavily on their microstructure. The microstructure is determined by the dynamics of the impact of the droplets on the substrate surface and the subsequent overlapping of the previously solidified and deformed droplets. Substrate preparation prior to spraying ensures strong adhesion of the coating. This includes roughening and preheating of the substrate surface. In the present study, the smoothed particle hydrodynamics (SPH) method is used to model the Al2O3 impact on a preheated substrate and a roughened substrate surface. A semi-implicit enthalpy–porosity method is applied to simulate the solidification process in the mushy zone. In addition, an implicit correction for SPH simulations is used to improve the performance and stability of the simulation. To investigate the dynamics of heat transfer in the contact between the surface and the droplet, the discretization of the substrate is also taken into account. The results show that the studied substrate surface conditions affect the splat morphology and the solidification process. Subsequently, the simulation of multiple droplets for coating formation is also performed and analyzed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Thermal spraying is a process in which molten or semi-molten particles are deposited on a prepared substrate. The metallic or non-metallic particles flatten on contact and form platelets called splats, with multiple layers of these splats forming the coating (Ref 1). Coating properties such as porosity, adhesion, and surface roughness depend on a number of parameters, such as morphology, condition and temperature of the substrate, temperature and velocity of the particle, particle morphology and particle size distribution. These parameters determine the shape of these splats and the way they are bonded to each other and to the substrate (Ref 2). To ensure strong adhesion of a thermally sprayed coating, the substrate needs to be carefully prepared. Typically, the surface is roughened by grit-blasting. Grit-blasting increases the surface area and leaves undercuts, which facilitate mechanical interlocking and thus enhancing adhesion of the coating on the substrate. In addition, the microstructure of the coating and its properties have a significant effect on fluid flow and heat transfer during droplet impact and are strongly influenced by substrate temperature (Ref 3, 4).
Therefore, a detailed understanding of the dynamics of particle impact on the substrate is essential for better control of the coating build-up. However, the deposition of particles during thermal spraying is not easy to observe experimentally, since the splat formation and solidification occur within a few microseconds. In this work, the impact of Al2O3 droplet deposited by atmospheric plasma spraying is numerically investigated. This article is built upon the previous work of the authors (Ref 5). In previous work, the authors have shown a quantitative analysis of the simulations of the impact of molten Al2O3 droplet with SPH discretization taking into account the droplet height, diameter and velocity distribution over time. In general, good agreement was found with the results simulated in finite volume method (FVM) discretization. The SPH method allowed for a higher discretization density in the region of interest while requiring only a quarter of the simulation time. In addition, the spread factor of droplet impact with different initial diameters was also calculated using the SPH solver. The results show good correlation with the analytical expression from the literature and with the results predicted by Farrokhpanah et al. (Ref 6). The molten droplet is represented as an incompressible fluid. The phase change during solidification is modeled with a semi-implicit enthalpy–porosity method. An implicit correction for SPH simulations is also added to improve performance and simulation stability. The previous simulation model is extended to include additional surface conditions of the substrate to understand the influence of substrate preparation prior to coating. First, the heat transfer from the droplet to the substrate is taken into account. In this case, the substrate with different initial temperatures and its effect on the deposited splat is analyzed. Then, a substrate with a rough surface is introduced to the model, corresponding to real substrates prepared by grit-blasting. The results are then compared with the simulation result of a droplet impact on a flat surface. In this way, the effect of the rough surface on the adhesion of the droplet can be studied. Finally, the single droplet impact is extended to 20 droplet impacts to simulate a coating build-up using the SPH method for the first time, which was previously done using the VOF method.
Related Work
The simulation of particle impacts and coating behavior of thermal spray processes has been attempted using wide variety of models and discretization methods. The most common approach so far has been to use an Eulerian grid alongside the volume-of-fluid (VOF) method. However, during impact the molten particle deforms from roughly spherical to a thin layer, which is difficult to resolve accurately with a fixed grid resolution using these methods. Solution methods, such as spatially adaptive discretizations, typically come at the cost of reduced performance and increased implementation complexity. In addition, the cells containing fluid interfaces typically incur the largest computational cost, especially when these regions are adaptively sampled to higher resolutions (Ref 7).
Notable works using the VOF method are, e.g., the ones of Pasandideh-Fard et al. (Ref 8) and Zheng et al. (Ref 9). The former developed an approach for the 3D simulation of thermally sprayed particles onto a flat surface, including solidification. For solidification they applied a fixed velocity approach, where the solidified material was essentially treated as a boundary by setting infinite density and zero velocity. The latter instead used a momentum-sink approach for solidification, comparable to the approach used in this work.
These studies provided methods to improve the understanding of thermal spray processes, yet they generally required immense computational resources. In previous works of the authors, a modified momentum source approach was proposed (Ref 10) and later applied to multiple droplet impacts (Ref 11). These simulations were then applied to predict the effective thermal conductivity of the sprayed coatings (Ref 12).
In this work, the simulation of droplet impact on substrate with surface preparation and multiple droplet impacts using the Lagrangian smoothed particle hydrodynamics (SPH) method will be presented. This method originates in the field of astrophysics and was introduced by Gingold and Monaghan (Ref 13) and Lucy (Ref 14). Since then it has been adopted in a wide range of fields including engineering, medicine, physics and computer science and is most often used for the simulation of incompressible fluids. It is also a very appealing method to simulate droplet impact in thermal spraying, because of its ability to deal with free surfaces and to natively handle topological changes. As such, there have been several works dealing with the simulation of droplet impact for thermal spraying using SPH.
Farrokhpanah et al. (Ref 6, 15), introduced a nonlinear enthalpy transformation method which simplifies the incorporation of the latent heat of melting. In their work they show a specific application to suspension plasma spraying. Fang et al. (Ref 16) proposed a method for simulating droplet spreading and solidification. This includes a pressure correction scheme and an artificial heat model based on internal energy. They also utilized a momentum-sink for phase change. Zhang et al. (Ref 17) made use of a very similar approach without pressure correction, yet also considering substrate melting for high thermal conductivities.
A hybrid approach was pursued by Abubakar and Arif (Ref 18) where SPH and the Finite-Element Method (FEM) are combined. SPH is used to model the liquid phase while FEM is used to model the solidification process and compute residual stresses. Another hybrid approach is also employed by Zhu et al. (Ref 19) where spray deposition of semi-molten ceramic droplets is simulated. Recently, Lee et al. (Ref 20) investigates yttria-stabilized zirconia droplet impact under different substrate temperatures. The outcome shows that a higher substrate temperature can cause more splashes because of slower heat transfer from the droplet to the substrate.
Computational Method
Here we briefly describe the SPH discretization method in general and the specific models used for droplet impact. For an in depth explanation the reader is referred to previous work of the authors (Ref 5).
SPH discretizes the continuum by a specific number of Lagrangian particles, i.e., typically particles with specified mass, whose movement is tracked throughout the simulated domain and time. In order to approximate an arbitrary scalar quantity \(A\left({\mathbf{x}}_{i}\right)\) at position \({\mathbf{x}}_{i}\in {\mathbb{R}}^{3}\), the following summation is used
where \(W\left(\mathbf{x};h\right)\) denotes a compactly supported kernel function with smoothing length \({h}_{\text{smooth}}\) and \({\mathcal{N}}_{{x}_{i}}\) denotes the set of particles within the compact support around \({\mathbf{x}}_{i}\). Additionally, \({m}_{j}=m\left({\mathbf{x}}_{j}\right)\) denotes the mass and \({\rho }_{j}=\rho \left({\mathbf{x}}_{j}\right)\) the density at particle \(j\) in the neighborhood around \({\mathbf{x}}_{i}\). This shorthand will be used throughout the rest of this manuscript. The approximation in Eq 1 can be made because \(W\) approximates the \(\delta\)-distribution in the limit of \(\mathrm{lim_{h \rightarrow 0}}\), as well as fulfilling several other properties (Ref 21).
This approximation can also be used to compute differential operators on a set of points using
where the additional shorthand \({W}_{ij}\) denotes \(W\left({\mathbf{x}}_{i}-{\mathbf{x}}_{j};h\right)\). Other kinds of derivatives, including higher order derivatives can be computed analogously. However, there is some variation in the SPH differential operators regarding the numerical properties such as the order of consistency, numerical condition and symmetry to name a few. For detailed information on the fundamentals of SPH discretization the reader is again referred to the SPH surveys by Price (Ref 22) and Koschier et al. (Ref 21).
Model
The molten droplet along with the solidification process is simulated as an incompressible fluid with a Darcy term for solidification. The Navier–Stokes equations,
relate the local change in momentum to the pressure gradient \(\nabla p\), viscosity \(\mu {\nabla }^{2}\mathbf{v}\), surface tension \({{\varvec{f}}}_{\text{st}}\) and external forces \({{\varvec{f}}}_{\text{ext}}\) such as gravity. The discretization of each of these terms will be explained in the following.
Pressure
In order to compute the pressure forces, the (implicit) Divergence-Free SPH (DFSPH) pressure solver proposed by Bender and Koschier (Ref 23) is utilized. Compared to explicit pressure solvers, as are also often used in related works (Ref 6, 24), this implicit solver is able to strictly enforce the incompressibility while additionally guaranteeing a divergence-free velocity field, which has been shown to further improve the accuracy and stability of simulations.
Viscosity
The viscosity term in Eq 3 is also computed implicitly, using the model proposed by Weiler et al. (Ref 25). Instead of the native approach, which would explicitly discretize the viscosity force, the implicit model computes the viscosity force by solving the following equation
using a matrix-free conjugate gradient (CG) solver for the velocity \({\mathbf{v}}_{\text{visc}}^{t+1}\). Here \({\mathbf{a}}_{\text{visc}}\) denotes the acceleration due to viscosity, while \(\nu\) denotes the kinematic viscosity coefficient. The second derivative \({\nabla }^{2}{\mathbf{v}}_{\text{visc}}^{t+1}\) is discretized using a special symmetric form, which also conserves linear and angular momentum. The usage of implicit integration makes it possible to stably simulate effects with large time steps and surface tension coefficients.
Surface Tension and Compensation
The computation of surface tension forces is known to not be a trivial matter in SPH simulations. Due to the chaotic nature of the particles and the unclear definition of what constitutes a surface particle, a combination of two surface tension approaches is applied. The Continuum Surface Force (CSF) model implementation of Müller et al. (Ref 26) which computes the surface tension force using curvature and normals estimated from a smoothed color field is used. This approach is based on the CSF formulation of Brackbill et al. (Ref 27). However, it is known to yield error prone curvature values in the interior of the fluid and to become unstable when using larger surface tension coefficients.
In order to compensate for inaccurate surface tension forces and the effect of tensile instability at the surface, the inter-particle force (IPF) model introduced in the previous work of the authors (Ref 5) is additionally used. The main effect of this model is to restore some of the inherent cohesiveness of the fluid, which is lost when using pressure clamping in the pressure solver component.
Finally, XSPH as proposed by Monaghan (Ref 28) was also applied, which is a non-dissipative and momentum conserving way of coupling the velocities of neighboring particles. It was initially proposed to reduce the interpenetration and chaotic behavior of particles in the absence of viscosity forces, and is also often used in related work to improve the results.
Solidification
Depending on the treatment of the substrate, solidification can often be considered as one of the main factors which determine the dynamics of the thermal spray process. It can significantly affect the splat shape and coating quality, and as such affects coating properties.
In this paper, the solidification is modeled using a Darcy term (momentum-sink) in the Navier–Stokes equation, which adds a deceleration depending on the temperature of the material, typically once the temperature decreases below melting. This momentum-sink accounts for the movement of the semi-liquid state in the so-called mushy zone. This model was validated by the droplet impact model using the VOF method in previous work of the authors (Ref 5):
where \({{\varvec{a}}}_{\text{solid}}\) is the deceleration computed on a per-particle basis. Furthermore, \(C\) denotes the morphological constant, \(T\) the temperature, \({T}_{l}\) the liquidus temperature, \(\Delta {T}_{l}\) the temperature range of the mushy region and \({f}_{l}\) the liquid fraction. Note that the missing value in the last case of \({f}_{l}\) is due to the fact that solid particles are removed from calculation and are effectively treated as rigid objects for the remaining part of the simulation, while still taking heat transfer into account.
Heat Transfer
Due to the Lagrangian nature of the SPH discretization, convective heat transfer is naturally taken into account. As such, conductive heat transfer is computed as
which was proposed by Brookshaw (Ref 29) and also used by Zhang et al. (Ref 30). Here, \(h\) denotes the specific enthalpy, \(\Delta t\) the time step, \(\lambda\) the thermal conductivity and \({\mathbf{r}}_{ij}={\mathbf{x}}_{i}-{\mathbf{x}}_{j}\). Since both the enthalpy and temperature are taken into account, the temperatures are updated from enthalpy at the end of each time step.
In the case where heat transfer from the droplet to the substrate is considered, the thermal contact between the droplet and the substrate is implicitly affected by the distance between droplet SPH particles and substrate SPH particles. To this end, we have implemented the adhesion force with a correction term. The average particle distance from the substrate surface and the particle density on the substrate surface are effectively governed by our adhesion approach, which naturally models this thermal contact. The thermal contact would be improved by higher adhesion values, while thermal contact would be inhibited by lower values. This might be understood as describing the surface roughness of the sprayed surface on a macro scale. For a detailed description of the adhesion force, please refer to (Ref 5).
Simulation Domain
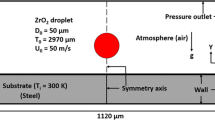
Given that the term particle is used for both the feedstock material in thermal spraying and the SPH method, the terminology should be properly distinguished. In the following, the term particle is used for the SPH discretization particle of the numerical method, while the molten feedstock material which is accelerated toward the substrate is called droplet. The simulation domain for the studied droplet impact is presented in Fig. 1. The Al2O3 droplet has a diameter of d = 45 µm and initial in-flight properties of temperature T = 2500 K and velocity v = 200 m/s. The droplet is discretized with particles having an individual radius of r = 0.4 µm and consists of a total of 91,136 particles.
In this paper, the substrate is modeled in four different ways:
-
As a flat surface with a Dirichlet and free-slip boundary condition with temperature TWall = 300 K,
-
As a grit-blasted surface with the same boundary conditions and wall temperature,
-
As a discretized substrate where heat transfer from droplet to the substrate is considered,
-
And as a discretized grit-blasted substrate where heat transfer from droplet to the substrate is considered.
These cases are intended to provide insight into a better process understanding of droplet impact in thermal spraying. According to Mostaghimi et al. (Ref 2) the estimated heat loss of the droplet to the surrounding gas is approximately three orders of magnitude less than that of heat conduction into the substrate. Therefore, the free surface of the droplet is assumed to be adiabatic in this study, i.e., the heat loss of the droplet to the surrounding gas is neglected in the present studies. The simulation model with discretized substrate takes into account temperature-dependent material properties, as well as the latent heat of melting. The martensitic stainless steel X105CrMo17 was used as substrate. A typical case for this is the application of a ceramic coating as a protective layer on this bearing steel. The material properties of the Al2O3 droplet and the X105CrMo17 stainless steel substrate for the case with discretized substrate are listed in Table 1.
The temperature-dependent material properties are shown in Fig. 2. The model was implemented in a custom branch of SPlisHSPlasH (Ref 31).

Adapted from Ref 5, available under CC BY 4.0 license at SpringerLink
Temperature-dependent material properties of droplet and substrate.
Results and Discussion
In this section, the results of the studied cases are presented. All simulations were computed using 32 computational cores of a high-performance cluster.
Droplet Impact on Preheated Substrate
The dynamics of heat transfer in the contact between surface and droplet is being investigated to analyze the influence of the substrate temperature on the deposited splat. In this case, the temperature-dependent material properties, latent heat of melting and heat transfer into the substrate are considered. The obtained splat shapes and spreading factors of the deposited splats are evaluated.
Pershin et al. (Ref 32) have shown that heating of the substrate can affect the impact and solidification of molten droplets and subsequently improve the coating adhesion. Therefore, simulation of droplet impact on a substrate with initial temperature of T0 = 300 K and T0 = 900 K was investigated to understand the influence of the preheated substrate on the deposited splat. Figure 3 depicts the splats deposited on a flat substrate with different initial temperatures. The initial diameter of the droplet is d0 = 45 µm. The droplet and substrate are discretized with a particle radius of r = 0.4 µm. This resulted in a total of 1,972,736 particles, consisting of 91,136 particles for the droplet and the rest for the substrate. The simulations are run up to a simulation time of ts = 4 µs. The diameters of the calculated splats on the non-preheated and the preheated substrate are ds = 94 µm and ds = 98 µm with a spread factor of ξ = 2.09 and ξ = 2.18, respectively. Similar tendency was also observed by McDonald et al. (Ref 33), where the splats obtained by impact on preheated substrate showed a larger final diameter due to a smaller thermal contact resistance. The computation time required to solve the droplet impact simulation on a substrate with T0 = 300 K and T0 = 900 K was about t = 125 and t = 202 min, respectively.
After impact, the droplet begins to spread. During spreading, the edges start to solidify and thus interrupt the flow of the spreading fluid. This phenomenon occurs faster on a non-preheated substrate due to the high temperature difference between the droplet and the substrate, resulting in a rapid temperature decrease, which leads to a smaller splat diameter with less splashes. On the other hand, the splat deposited on the preheated substrate has a larger diameter with more splashes. This effect is a result of a smaller initial temperature difference, causing a slower overall temperature decrease. This gives the droplet more time to spread out, which leads to a larger splat diameter. A similar correlation was observed in the experimental work of Wang et al. (Ref 34). Their results showed that an increase in substrate temperature enhances the spreading of the droplet, leading to a higher flattening ratio.
The temperature distributions of splat and substrate at the cross section are given in Fig. 4. When the droplet impacts on the substrate, heat transfer takes place at the interface. As a result, the temperature of the droplet decreases and the temperature of the substrate increases. For the substrate with T0 = 300 K, the temperature at the interface between the splat and the substrate increases up to T = 1100 K. In the case of the substrate with T0 = 900 K, the temperature at the interface rises to just above T = 1500 K. From the temperature profile along the y-direction of both cases at t = 2 µs, it can be seen that the temperature of the droplet impact on a substrate with T0 = 900 K decreases only slightly with a more moderate gradient at the interface than the temperature decrease for the droplet impact on a substrate with T0 = 300 K. This corresponds to the experimentally observed reduced cooling rate of the droplets impinging on the preheated surface and gives them more time to spread.
A magnification of the edge of both splats is shown in Fig. 4. The gradient of the edge produced by droplet impact on preheated substrate is lower than the droplet impact on a non-preheated substrate. This effect is a result of a smaller initial temperature difference between the droplet and the preheated substrate, causing a slower overall temperature decrease. This gives the droplet more time to spread out, which leads to a larger splat diameter. On the other hand, the spreading stopped earlier in the center of the splat than the edges, resulting in only a minor difference in the height of the splat.
Droplet Impact on Grit-Blasted Substrate
The SPH model was further used to simulate the droplet impact on a rough substrate corresponding to real prepared substrates. The surface topography of a typical substrate prepared for coating via grit-blasting with blasting pressure of p = 0.5 MPa and alumina grit, was obtained using a laser profilometer measurement. The surface data was imported into the model and has a surface roughness Ra = 6 µm.
Simulation of droplet impact on a grit-blasted substrate is compared to that on a flat surface to understand the effect of the rough surface on coating adhesion. The two cases of grit-blasted substrate as a wall with a constant temperature of T = 300 K and a discretized grit-blasted substrate with initial temperature of T0 = 300 K with heat transfer from the droplet to the substrate, were studied. The surface roughness creates increased effective surface area for heat transfer resulting in an increased cooling rate. On one hand, the droplet impact on such surfaces corresponds more to the real situation, but on the other hand is more complicated to analyze. For the case of the droplet impact on a rough substrate surface with heat transfer, the discretization of the droplet and substrate resulted in a total of 3,520,932 particles.
Figure 5 shows the droplet impact, the subsequent spreading and solidification process on a flat surface, grit-blasted substrate surface, and discretized grit-blasted substrate, respectively. All calculations were run until simulation time of ts = 4 µs. The computation time required to solve the simulations is about tc = 3 min, tc = 15 min and tc = 607 min, respectively. The simulation of droplet impact on a discretized, grit-blasted substrate required a much longer computation time since the substrate was also spatially discretized, resulting in a significantly larger number of particles. In all cases, the droplet spreading ends at ca. ts = 1.2 µs while the splat continues to solidify even afterward.
Both results of droplet impact on a grit-blasted surface show irregular splat morphology compared to the perfectly disk-shaped splat as a result of droplet impact on a flat substrate. It can also be observed, that the splats filled in the surface created by the grit-blasting. Moreover, in the real process the material splashed off after droplet impact is often not redeposited on the substrate, but instead considered as material loss. This suggests that the substrate surface not only affects the splats morphology, but also the deposition efficiency due to the changing flows in the fluid.
Not only the substrate surface plays an essential role for the splat morphology, also the heat transfer from the droplet to the substrate is of importance. Compared to the simulation result without heat transfer onto the substrate, the droplet is immediately cooled to T = 300 K upon contact, as can be seen in Fig. 6(a). This effect propagates upward to the top of the splat preventing further spreading of the droplet, so that less splashing is observed. On the other hand, the temperature at the interface is still more than T = 1000 K when heat transfer is taken into account, as shown in Fig. 6(b).
Coating Build-up Simulation
The simulation of the impact of a single droplet on a flat surface using the SPH method resulted in a much shorter simulation time than the VOF method, as shown in previous study (Ref 5). This promises a coating build-up simulation not only of individual droplets but also of the entire coating in a reasonable time. Therefore, a first attempt of coating build-up was simulated with 20 Al2O3 droplets with an initial diameter of d0 = 45 µm and initial velocity of v0 = 200 m/s. The substrate was modeled as a flat surface with TWall = 300 K. The droplets are randomly generated with varying initial positions within the dimensions with a length of l = 225 µm and a width of w = 225 µm with a time interval of ts = 1 µs between each droplet. The droplets were each discretized with particles with a radius of r = 0.4 µm, resulting in total 1,822,720 particles. The calculation was run until a simulation time of ts = 30 µs. The computation time required to solve the simulation was roughly tc = 41 h.
Although the simulation was not performed on a rough grit-blasted surface, it can be assumed that the surface roughness was incorporated indirectly through the first layer of the coating. The coating obtained is presented in Fig. 7. As can be seen in Fig. 7(a), the splashes do not leave the defined domain as in VOF method, but continue to be tracked. Not only does the fine discretization of the droplets contribute to the rather extensive computation time, but also the tracking of the individual particles throughout the simulation domain and time.
Figure 7(b) depicts the extracted coating build-up on a substrate with l = 225 µm and w = 225 µm. Defects in thermally sprayed coatings such as voids can be seen in the cross section in Fig. 7(c). The splashing and fragmentation of the molten droplets on impact, as observed by McDonald et al. (Ref 35), could potentially lead to the voids observed in the coating. This indicates that the current SPH model, with some modifications, may be used in the future work for predicting coating microstructures, and thus coating properties.
Conclusion
The previous model of the authors (Ref 5) for the investigation of droplet impact was expanded. The simulation model was extended to study the droplet impact on substrate with surface preparation. These include substrates with different initial temperatures and a real surface model which was prepared via grit-blasting for coating. In addition, a first coating build-up of 20 Al2O3 droplets has been successfully simulated and evaluated.
The following results were observed:
-
The simulation of droplet impact on the preheated substrate showed a larger splat diameter with more splashes compared to a droplet impact on the substrate at room temperature.
-
The droplet impact on a real prepared substrate showed irregular splat morphology compared to the perfectly disk-shaped splat as a result of droplet impact on a flat substrate.
-
The droplet filled in the undercuts produced by the grit-blasting, resulting in mechanical interlocking between the splat and substrate.
-
The simulation of the coating build-up also revealed a promising result, in which voids between the splats can be detected.
With the assumptions in the numerical model and partly temperature-dependent material properties, the process of droplet impact can be qualitatively simulated. This model can be further extended, e.g., by a surface tension model and a temperature-dependent viscosity model, to allow more accurate prediction of the coating properties.
Abbreviations
- d :
-
Diameter
- d 0 :
-
Initial droplet diameter
- d s :
-
Splat diameter
- l :
-
Length
- p :
-
Pressure
- r :
-
Discretization particle radius
- T :
-
Temperature
- T 0 :
-
Initial temperature
- t :
-
Time
- t c :
-
Computation time
- t s :
-
Simulation time
- T wall :
-
Temperature for the wall boundary condition
- v :
-
Velocity
- v 0 :
-
Initial droplet velocity
- w :
-
Width
- ξ :
-
Spread factor
- Droplet:
-
For the molten feedstock material which is accelerated toward the substrate
- Particle:
-
For the SPH discretization particle of the numerical method
References
P.L. Fauchais, J.V.R. Heberlein, and M.I. Boulos, Overview of thermal spray, In: Thermal spray fundamentals: from powder to part, P.L. Fauchais, J.V. Heberlein, and M.I. Boulos, (Eds.), (Springer US, 2014), pp. 17-72.
J. Mostaghimi and S. Chandra, Droplet impact and solidification in plasma spraying, Springer International Publishing, Handbook of Thermal Science and Engineering, 2018, p 2967-3008
A. Abedini, A. Pourmousa, S. Chandra and J. Mostaghimi, Effect of Substrate Temperature on the Properties of Coatings and Splats Deposited By Wire Arc Spraying, Surf. Coat. Technol., 2006, 201(6), p 3350-3358.
O. Sarikaya, Effect of the Substrate Temperature on Properties of Plasma Sprayed Al2o3 Coatings, Mater. Des., 2005, 26(1), p 53-57.
S.R. Jeske, J. Bender, K. Bobzin, H. Heinemann, K. Jasutyn, M. Simon, O. Mokrov, R. Sharma, and U. Reisgen, Application and Benchmark of Sph For Modeling the Impact in Thermal Spraying, Comput. Particle Mech., 2022.
A. Farrokhpanah, J. Mostaghimi and M. Bussmann, Nonlinear Enthalpy Transformation for Transient Convective Phase Change in Smoothed Particle Hydrodynamics (Sph), Numer. Heat Transf. Part B Fundam., 2021, 79(5–6), p 255-277.
R. Borrell, O. Lehmkuhl, and J. Castro, Parallelization Strategy for the Volume-Of-Fluid Method on Unstructured Meshes, Procedia Eng. (2013), 61.
M. Pasandideh-fard, S. Chandra and J. Mostaghimi, A Three-Dimensional Model of Droplet Impact and Solidification, Int. J. Heat Mass Transf., 2002, 45, p 2229-2242.
Y.Z. Zheng, Q. Li, Z.H. Zheng, J.F. Zhu and P.L. Cao, Modeling the Impact, Flattening and Solidification of a Molten Droplet on a Solid Substrate During Plasma Spraying, Appl. Surf. Sci., 2014, 317, p 526-533.
K. Bobzin, M. Öte, M.A. Knoch, I. Alkhasli and S.R. Dokhanchi, Modelling of Particle Impact Using Modified Momentum Source Method in Thermal Spraying, IOP Conf. Series: Mater. Sci. Eng., 2019, 480, p 12003.
K. Bobzin, W. Wietheger H. Heinemann, Hendrik and I. Alkhasli, Simulation of multiple particle impacts in plasma spraying, In: Enhanced material, parts optimization and process intensification, U. Reisgen, D. Drummer, and H. Marschall, (Eds)., (Springer International Publishing, 2021), p. 91-100.
K. Bobzin, W. Wietheger, H. Heinemann and F. Wolf, Simulation of Thermally Sprayed Coating Properties Considering the Splat Boundaries, IOP Conf. Series: Mater. Sci. Eng., 2021, 1147, p 12026.
R.A. Gingold and J.J. Monaghan, Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars, Monthly Not. Royal Astron. Soc, 1977, 181, p 375-389.
L.B. Lucy, A Numerical Approach to the Testing of the Fission Hypothesis, Astron. J., 1977, 82, p 1013-1024.
A. Farrokhpanah, M. Bussmann and J. Mostaghimi, New Smoothed Particle Hydrodynamics (Sph) Formulation for Modeling Heat Conduction With Solidification and Melting, Numer. Heat Transf., Part B: Fundam., 2017, 71(4), p 299-312.
H.S. Fang, K. Bao, J.A. Wei, H. Zhang, E.H. Wu and L.L. Zheng, Simulations of Droplet Spreading and Solidification Using an Improved Sph Model, Numer. Heat Transf. Part A Appl., 2009, 55(2), p 124-143.
M.Y. Zhang, H. Zhang and L.L. Zheng, Simulation of Droplet Spreading, Splashing and Solidification Using Smoothed Particle Hydrodynamics Method, Int. J. Heat Mass Transf., 2008, 51(13–14), p 3410-3419.
A.A. Abubakar and A.F.M. Arif, A Hybrid Computational Approach for Modeling Thermal Spray Deposition, Surf. Coat. Technol., 2019, 362, p 311-327.
Z. Zhu, S. Kamnis and Gu. Sai, Numerical Study of Molten and Semi-Molten Ceramic Impingement By Using Coupled Eulerian and Lagrangian Method, Acta Mater., 2015, 90, p 77-87.
J. Lee, K.K. Subedi, G.W. Huang, J. Lee, and S.-C. Kong, Numerical Investigation of Ysz Droplet Impact on a Heated Wall for Thermal Spray Application, J. Thermal Spray Technol. (2022).
D. Koschier, J. Bender, B. Solenthaler and M. Teschner, A Survey on Sph Methods in Computer Graphics, Comput. Gr. Forum, 2022, 41(2), p 737-760.
D.J. Price, Smoothed Particle Magnetohydrodynamics–Iv. Using the Vector Potential, Monthly Notices Royal Astron. Soc., 2010, 401(3), p 1475-1499.
J. Bender and D. Koschier, Divergence-free smoothed particle hydrodynamics, In: Acm Siggraph/Eurographics Symposium on Computer Animation, (2015), p 1-9.
J.J. Monaghan, Smoothed Particle Hydrodynamics and Its Diverse Applications, Annu. Rev. Fluid Mech., 2012, 44(1), p 323-346.
M. Weiler, D. Koschier, M. Brand, and J. Bender, A Physically Consistent Implicit Viscosity Solver for Sph Fluids, Comput. Gr. Forum, 7(2) (2018).
M. Müller, D. Charypar, and M. Gross, Particle-based fluid simulation for interactive applications, In: Acm Siggraph/Eurographics Symposium on Computer Animation, (2003), p 154-159.
J.U. Brackbill, D.B. Kothe and C. Zemach, A Continuum Method For Modeling Surface Tension, J. Comput. Phys., 1992, 100(2), p 335-354.
J.J. Monaghan, On the Problem of Penetration in Particle Methods, J. Comput. Phys., 1989, 82(1), p 1-15.
L. Brookshaw, A Method of Calculating Radiative Heat Diffusion in Particle Simulations, Publ. Astron. Soc. Austral., 1985, 6(2), p 207-210.
M. Zhang, H. Zhang and L. Zheng, Numerical Investigation of Substrate Melting and Deformation During Thermal Spray Coating By Sph Method, Plasma Chem. Plasma Process., 2008, 29(1), p 55-68.
J. Bender, Splishsplash. (2021) https://github.com/InteractiveComputerGraphics/SPlisHSPlasH.
V. Pershin, M. Lufitha, S. Chandra and J. Mostaghimi, Effect of Substrate Temperature on Adhesion Strength of Plasma-Sprayed Nickel Coatings, J. Therm. Spray Technol., 2003, 12(3), p 370-376.
A. McDonald, C. Moreau and S. Chandra, Thermal Contact Resistance Between Plasma-Sprayed Particles and Flat Surfaces, Int. J. Heat Mass Transf., 2007, 50(9), p 1737-1749.
J. Wang, X.-T. Luo, C.-J. Li, N. Ma and M. Takahashi, Effect of Substrate Temperature on the Microstructure and Interface Bonding Formation of Plasma Sprayed Ni20cr Splat, Surf. Coat. Technol., 2019, 371, p 36-46.
A. McDonald, M. Xue, S. Chandra, J. Mostaghimi and C. Moreau, Modeling Fragmentation of Plasma-Sprayed Particles Impacting on a Solid Surface at Room Temperature, Comptes Rendus Mécanique, 2007, 335(5), p 351-356.
Acknowledgments
The presented investigations were carried out at RWTH Aachen University within the framework of the Collaborative Research Centre SFB1120-236616214 “Bauteilpräzision durch Beherrschung von Schmelze und Erstarrung in Produktionsprozessen” and funded by the Deutsche Forschungsgemeinschaft e.V. (DFG, German Research Foundation). The sponsorship and support are gratefully acknowledged. Simulations were performed with computing resources granted by RWTH Aachen University under project rwth0570.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is an invited paper selected from presentations at the 2022 International Thermal Spray Conference, held May 4–6, 2022 in Vienna, Austria, and has been expanded from the original presentation. The issue was organized by André McDonald, University of Alberta (Lead Editor); Yuk-Chiu Lau, General Electric Power; Fardad Azarmi, North Dakota State University; Filofteia-Laura Toma, Fraunhofer Institute for Material and Beam Technology; Heli Koivuluoto, Tampere University; Jan Cizek, Institute of Plasma Physics, Czech Academy of Sciences; Emine Bakan, Forschungszentrum Jülich GmbH; Šárka Houdková, University of West Bohemia; and Hua Li, Ningbo Institute of Materials Technology and Engineering, CAS.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bobzin, K., Heinemann, H., Jasutyn, K. et al. Modeling the Droplet Impact on the Substrate with Surface Preparation in Thermal Spraying with SPH. J Therm Spray Tech 32, 599–608 (2023). https://doi.org/10.1007/s11666-023-01534-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11666-023-01534-0