Abstract
Deposition efficiency (DE) serves as a key performance indicator in plasma spraying, which is tailored by dozens of intrinsic and extrinsic influencing factors. Due to the nonlinear and complex interdependencies of the influencing factors, increasing DE has always been a challenging undertaking in the process development of plasma spraying. Hence, employing modern computer-aided algorithms is inevitable to overcome these complexities. In this study, an expert system is developed to predict DE from process parameters using adaptive neuro-fuzzy inference system (ANFIS) and support-vector machine (SVM). The developed expert system consists of two subsystems: (1) SVM-models from a previous work of the authors are used to predict the in-flight particle properties from different process parameters based on simulation data sets and (2) an ANFIS is developed to predict DE from in-flight particle properties based on experimental data sets. The results show that the developed expert system is able to estimate DE precisely with root-mean-square error (RMSE) of about 1.1%. The proposed system enables sustainable and cost-effective coatings through the prediction of DE for each set of process parameters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The coating properties in atmospheric plasma spraying (APS) are a function of three interdependent subsystems in general: (1) the generation of the plasma jet, (2) the injection and interaction of the feedstock material with the plasma jet that meanwhile mixes with the surrounding gas and (3) the impact and solidification of the particles on the substrate (Ref 1). During each subsystem, several physicochemical mechanisms occur, which lead to the formation of a coating. These mechanisms include momentum and heat transfers from the plasma jet to the particles prior to impact and during solidification, as well as mass transfers caused by partial vaporization of the particles in the plasma plume. Therefore, each subsystem has a large number of variables that influence the plasma spraying process.
The influencing factors involving in the coating architecture result from the combination of intrinsic and extrinsic parameters. The directly adjustable extrinsic parameters include, for instance, the electrical current and the volume flow rates of the process gases. The resulting intrinsic parameters, such as in-flight particle velocities and temperatures, can only be influenced indirectly (Ref 2). All these parameters are interrelated and usually follow nonlinear relationships. For example, the variation of the current or the process gas flow to change the particle temperatures and velocities at impact, also generally requires adjusting the parameters for injection the feedstock material to obtain thermally and kinematically matched parameters. Furthermore, the combinations of these parameter sets are also influenced by disturbance variables, which subsequently can have an impact on the process stability and thus the reproducibility of the coatings. These disturbance variables can be categorized into common and special causes (Ref 3). In this context, the common influencing variables are related to a large number of random disturbance variables together, whose influence on the process cannot be quantified in detail. However, their effects on process stability can only be quantified by varying individual parameters. An example in APS is the fluctuation of the arc or the wear of the system components, e.g., electrodes and injectors. The special influencing variables are attributed to the malfunctioning of the equipment and some external influences that are statistically unpredictable. Examples are, among others, plasma gas impurities or not calibrated control devices (Ref 4).
The number of influencing factors in APS is estimated to be more than 200 variables (Ref 3). It should be emphasized that many of these factors are intimately connected by complicated nonlinear relationships. These interactions further increase the complexity of the overall APS system. Taking the above aspects into account, the question of robust methods for quantifying the complex interactions between the dozens of influencing factors in APS arises. It turns out that computer-aided algorithms can best fulfill this challenging undertaking. Artificial intelligence (AI) methods are suitable tools to investigate complex processes with parameter dependencies.
Previous research studies have used AI approaches to mainly forecast process parameters in order to attain the desired in-flight particle properties or coating characteristics. There have already been studies at the Surface Engineering Institute (IOT) at the RWTH Aachen University to analyze process data, coating properties and plasma jet characteristics using artificial neural network (ANN) and Design of Experiment (DoE) (Ref 5, 6). In other studies, Guessasma et al. (Ref 7) developed an ANN model to predict the in-flight particle characteristics of plasma-sprayed Al2O3-13 wt.% TiO2 feedstock material. Kanta et al. (Ref 8) implemented ANN and fuzzy logic (FL) to predict the in-flight particle properties as a function of process parameters for deposition of alumina-titania by APS. They concluded that the ANN model appeared well-suited for process prediction, whereas the FL model seemed more adapted for process control. In another work of Kanta et al. (Ref 9), an expert system was created by ANN and FL to control and adjust the process parameters so that constant values for the in-flight particle properties can be maintained. They aimed to account for the instabilities and intrinsic fluctuations inherent in the APS process based on the pre-defined rules of the FL model. Liu et al. (Ref 10) developed an expert system by implementation of ANN models and FL controllers to predict and control the in-flight particle properties and operating parameters. Similar to the work of Kanta et al., they predefined the fuzzy rules manually according to experimental data. As the use of ANN and FL revealed drawbacks such as reliance on a significant quantity of experimental data and taking too much time in construction of the rules, the adaptive neuro-fuzzy inference system (ANFIS) was employed in subsequent works due to its high prediction accuracy and low execution time (Ref 11). Datta et al. (Ref 12) aimed to predict coating properties from process parameters in APS by developing an ANFIS, which was tuned using a genetic algorithm (GA) and particle swarm optimization algorithm (PSO), separately. They found that the PSO-based approach performed better than the GA-based optimization in predicting the responses. Furthermore, Wu (Ref 13) developed an empirical model by combination of ANN and ANFIS to investigate the effect of process parameters on the coating properties in APS.
High deposition efficiency (DE) has always been one of the primary aims in the development of plasma spraying process in order to create cost-effective coatings in industrial production. DE is one of the key performance indicators for the productivity and consequential sustainability of the APS process. Although studies have been conducted to develop expert systems for predicting particle or coating properties, the research in investigating the interactions between process parameters, in-flight particle properties and DE remains limited. One of the obstacles in this regard is the lengthy and time-consuming data collection to measure DE for different process parameters. Therefore, the objective of this study is to demonstrate proof of concept for development of an expert system trained with the data sets of spatially resolved deposition efficiency on the substrate, namely local deposition efficiency (LDE), to predict the global DE from particle properties and process parameters. In the following, the architecture of the expert system is described in detail.
Architecture of Expert System
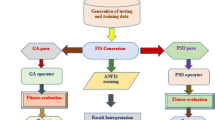
The overall architecture of the expert system is depicted in Fig. 1. This expert system consists of two subsystems: (1) SVM-models from a previous work of the authors are used to predict the in-flight particle properties from different process parameters based on simulation data sets and (2) an ANFIS is developed to predict DE from the in-flight particle properties based on experimental data sets of LDE. The setups of the SVM and ANFIS models as well as the LDE measurements are described in the following subsections.
Support-Vector Machine (SVM)
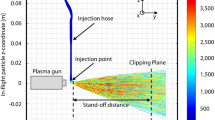
SVM is a supervised learning technique that employs structural risk minimization and a symmetric loss function that equally penalizes both high and low errors (Ref 14). SVM has the benefit that, despite the fact that its training includes nonlinear optimization, the associated objective function is convex, thus every local solution also reflects a global optimum (Ref 15). As a result, SVM has great generalization capability, with high prediction accuracy. The SVM models used in this study are based on a previous work of the authors about prediction of particle properties by machine learning (Ref 16). The training setup of the SVM models is illustrated in Fig. 2.
As a first step, former CFD models of a multi-arc APS process, developed at the IOT at the RWTH Aachen University, are used to generate the training data for the SVM models. In Fig. 2, the use of data from the already developed models is referred to as data recycling. The advantage of using simulation data is that a wide range of process parameters can be covered, while providing that much experimental data is hardly possible. A detailed description of the numerical modeling used in this study can be found in (Ref 17 and 18). Furthermore, the plasma generator and the plasma jet models were validated by experimental measurements (Ref 19). In the next step, DoE is implemented to cover a set of representative input process parameters for the SVM-models. The parameter setup for the DoE is given in Table 1.
Totally six different process parameters are considered for the DoE approach: primary gas flow (Argon), electric current, carrier gas flow, powder feed rate, particle size distribution at the injection point and standoff distance. Overall 45 simulations are performed, which corresponds to the Central Composite Design (CCD) method with 6-factor fractional design. Each simulation contains 2000 particle trajectories. As part of an automated data preparation pipeline, several sets of process parameters with corresponding particle properties are acquired from the CFD simulations and prepared as training and test data for the SVM models. From each 45 simulations, 75% of the data are used as training data and the remaining 25% as test data. Regarding the 45 simulations and up to 2,000 particle trajectories per simulation, the training data contain 64,858 particles and the test data amount to 21,612 particles. Please notice that due to different process parameters within each simulation, not all of the 2,000 simulated particle trajectories can reach the defined standoff distance by the CCD test design. Therefore, the exact number of particles for each simulation used to develop the SVM models may differ. The inputs of the prediction models are the process parameters listed in Table 1. The outputs of the SVM models in this study are the particle properties including the in-flight particle temperatures \({T}_{p}\) [K], velocities \({v}_{p}\) [m/s] and sizes \({D}_{p}\) [µm] at specific standoff distances. Please refer to (Ref 16) for further details regarding the development of the SVM models.
Adaptive Neuro-Fuzzy Inference System (ANFIS)
Fuzzy logic, originally presented by Lotfi A. Zadeh in the 1960s (Ref 20), is well recognized for its feature to model complex and ill-defined systems with cognitive uncertainties. FL employs linguistic if–then rules similar to human experience to qualitatively characterize a system without relying on exact quantitative analysis of nonlinear correlations among input and output parameters of the system. A fuzzy inference system (FIS) basically comprises a fuzzifier, a block of database and rule base that is jointly referred to as knowledge base, a decision-making unit and a defuzzifier, see Fig. 3. The fuzzification interface converts the crisp inputs into degrees of match with linguistic values. The rule base contains a number of fuzzy if–then rules and the database defines the membership functions (MF) of the fuzzy sets used in the fuzzy rules. MF quantifies the degree to which an input element belongs to a particular fuzzy set. The values mapped by a MF are known as grade or degree of membership, and they range from 0 to 1. The inference operations on the rules are performed by the decision-making unit and finally the defuzzification interface transforms the fuzzy results of the inference into a crisp output. Fuzzy if–then rules are expressions in form of IF \(x\) is \(A\) THEN \(z\) is \(B\), where \(A\) and \(B\) are labels for fuzzy sets characterized by suitable membership functions. The IF part is also called premise and the THEN part is referred to as consequence. This brief form of problem description facilitates the integration of human knowledge to deal with an uncertain and imprecise environment.
Due to insufficient knowledge, faults, or the complexity of the ill-defined system, FL is not optimal for achieving desired results in certain situations. For instance, developing a knowledge base for the stochastic process of plasma spraying, depends on instinct and experience and is therefore an iterative and challenging task (Ref 21). Moreover, the human-determined membership functions differ from person to person and from time to time. On the other hand, ANN provides interesting benefits such as learning capability, adaptability, optimization and generalization. In the 1990s, Jyh-Shing Roger Jang (Ref 22) integrated the best features of ANN and FL, and proposed his novel architecture under the terminology adaptive neuro-fuzzy inference system (ANFIS). ANFIS uses a feed-forward neural network to automatically construct and tune rule bases and MF parameters from given sample data sets. Therefore, it leverages not only the advantages of neural networks but also the idea of conditional statements for uncertain systems. Figure 4 shows the general architecture of ANFIS with five layers, each of which is made up of several nodes. The inputs of each layer are obtained by the nodes from the previous layer, similar to a neural network. For the sake of simplicity, the considered system is assumed to have two inputs \(x\) and \(y\), one output \(z\) and two fuzzy if–then rules as follows (Ref 22):
Rule 1: If \(x\) is \({A}_{1}\) and \(y\) is \({B}_{1}\), then \({f}_{1} ={p}_{1}x+{q}_{1}y+{r}_{1}\)
Rule 2: If \(x\) is \({A}_{2}\) and \(y\) is \({B}_{2}\), then \({f}_{2} ={p}_{2}x+{q}_{2}y+{r}_{2}\)
where \({A}_{i}\) and \({B}_{i}\) in the premise part are linguistic labels that are represented by fuzzy sets and characterized by an appropriate MF, while \({p}_{i}\), \({q}_{i}\) and \({r}_{i}\) are the consequent parameters of the \(i\)-th rule. The node functions in each layer are described below.
Layer 1: Every node \(i\) in the first layer is an adaptive node and has the output \({O}_{i}^{1}\) with a node function according to Eq 1, where \(\mu_{{A_{i} }}\) denotes the MF of \(A_{i}\) and it specifies the degree to which the given \(x\) satisfies the quantifier \(A_{i}\).
In this study, Gaussian membership functions have been used according to Eq 2, where \(\left\{ {a_{i} , c_{i} } \right\}\) is the parameter set that can be adapted to form various forms of Gaussian MFs. Parameters in this layer are referred to as premise parameters (Ref 22).
Layer 2: Every node in this layer is a fixed node labeled with \(\prod\) that multiplies the incoming signals and sends the product out. A sample node function in this layer is given in Eq 3, where \(w_{i}\) represents the so-called firing strength or degree of match with the premise part of the \(i\)-th rule.
Layer 3: Every node in this layer is a fixed (non-adaptive) node labeled with \(N\). The node function in this layer calculates the ratio of the \(i\)-th rule’s firing strength to the sum of all rules’ firing strengths according to Eq 4. The term \(\overline{w}_{i}\) is referred to as normalized firing strength (Ref 22).
Layer 4: Every node in this layer is an adaptive node. The node output of the fourth layer is the product of the respective previously found normalized firing strength with the consequent part of the respective rule, as given in Eq 5. In Eq 5, \(\overline{w}_{i}\) is the output of the third layer and \(\left\{ {p_{i} , q_{i} ,r_{i} } \right\}\) is the set of adaptive parameters of the fourth layer, namely consequent parameters.
Layer 5: The single node in this layer is a fixed node labeled with \(\sum\) that computes the overall output \(O_{i}^{5}\) as the summation of all incoming signals according to Eq 6. The final output of the system is the weighted average over all rule outputs.
In the literature, several kinds of fuzzy reasoning have been introduced (Ref 23). Mamdani (Ref 24) and Takagi–Sugeno (Ref 25) are the two most well-known types of FIS. The most fundamental difference between these two FIS types is the way the crisp output is generated from the fuzzy inputs. Mamdani employs defuzzification of a fuzzy output, whereas Sugeno computes the crisp output using weighted average. As a result, the computationally expensive defuzzification process is bypassed in Sugeno (Ref 26). The type of FIS in Fig. 4 is Sugeno. This can be noticed from the two earlier stated rules, as the fuzzy sets are involved only in the premise parts, while the consequent parts are described by a non-fuzzy equation of the input variable. The Mamdani-type has a more interpretable rule base and is well-suited to human input; a good example of its application field would be medical diagnostics. The Sugeno-type has more flexibility in system design, is computationally efficient and works well with optimization and adaptive techniques (Ref 26). Hence, the Sugeno-type FIS has been implemented in this study.
The adaptive parameters of the ANFIS model in this study are tuned using a data-driven hybrid learning algorithm. The hybrid method consists of backpropagation for the parameters associated with the input membership functions or premise parameters, and least squares estimation (LSE) for the parameters associated with the output membership functions or consequent parameters (Ref 22).
In the forward pass of the hybrid learning algorithm, the premise parameters are fixed and the consequent parameters are identified by the LSE technique. Let \(X\) be an unknown vector with the size of \(M\) whose elements are consequent parameters, and let \(B\) be the vector of training data with the size of \(P\), then it can be shown that the matrix equation \(AX{ } = { }B\) can be obtained in the adaptive network, where the dimension of \(A\) \(is\) \(P \times M\). The LSE technique estimates the vector of consequent parameters by minimizing the squared error \(||AX{ } - { }B||^{2}\). The least squares estimate of \(X\), denoted by \(X^{*}\), is given by Eq 7 (Ref 22)
where \(A^{T}\) is the transpose of \(A\).
In the backward pass, the error rates propagate backward and the premise parameters are updated by the gradient descent method, while the consequent parameters are fixed. The error measure for the p-th (\(1 \le p \le P\)) entry of training data can be obtained as the sum of squared errors according to Eq 8.
where \(T_{m,p}\) is the m-th component of p-th target output vector, and \(O_{m,p}^{L}\) denotes the m-th component of actual output vector produced by the p-th input vector. The overall error \(E\) can be calculated by using Eq 9.
The set of premise parameters can be obtained through the backpropagation procedure that implements gradient descent in \(E\) over the parameter space. Let \(\alpha\) be a premise parameter of the given adaptive network, then the update formula for the parameter \(\alpha\) is
In Eq 10, \(\eta\) is the learning rate, which depends on the length of each gradient transition in the parameter space. Please refer to (Ref 22) for further detail regarding the hybrid learning algorithm in an adaptive network.
Figure 5 depicts the block diagram of the optimization algorithm to tune FIS parameters. As shown in Fig. 5, the optimization algorithm creates potential FIS parameter sets during training. The fuzzy system is updated with each parameter set and then the input training data are used for evaluation. The cost for each solution is determined by the difference between the output of the fuzzy system and the expected output values from the training data.
The training setup of the ANFIS model developed in this study is shown in Fig. 6. The training data consist of experimental in-flight particle properties and their corresponding spatially resolved deposition efficiency on the substrate, namely local deposition efficiency (LDE). In a previous work of the authors, LDE was calculated based on spatial distribution of the particle mass flow rate in the free jet and the mass of the deposited feedstock material locally on the substrate (Ref 27). The motivation for using spatially resolved deposition efficiency is that a relatively broad database of particle properties and LDE on the substrate can be obtained, while providing that much data for the global DE together with the corresponding in-flight particle diagnostic measurements is hardly practical. Therefore, the overall objective of this study is to provide a proof of concept for the development of an expert system trained with the spatially resolved depositional efficiency to predict the global DE. As shown in Fig. 6, before developing the ANFIS model to predict DE, the training data were augmented using the k-nearest neighbor (k-NN) algorithm to enhance the model accuracy in terms of automatic generation of the rule base and membership functions. This technique uses k closest training data to a particular sample point in our experimental database to increase the diversity and the amount of data before training the ANFIS model. In the following subsection, the experimental setup for determination of LDE to be used as training data for the ANFIS model is presented. Subsequently, the results of each block of the introduced expert system are presented and discussed in Sect. Results and Discussion in detail.
Local Deposition Efficiency (LDE)
To calculate the spatially resolved deposition efficiency on the substrate, first a methodology was developed to estimate the distribution of the particle mass flow rate in the plasma jet (Ref 28). For this purpose, the entire free jet transverse section was divided into several non-overlapping focal planes. The sizes and velocities of the in-flight particles were measured at these focal planes by the optical particle diagnostic system HiWatch CS from Oseir Ltd., Tampere, Finland. Furthermore, the in-flight particle temperatures were captured in a measurement grid normal to the gun axis by the diagnostic system DPV-2000 from Tecnar Automation Ltd., St. Bruno, QC, Canada. Please consider that the HiWatch system has the advantage to capture the entire free jet with smaller number of individual measurements, since it has a relatively large measurement volume (Ref 28). Experiments were conducted with the three-cathode plasma generator TriplexPro™-210, Oerlikon Metco, Kelsterbach, Germany, at a spray distance of y = 100 mm. A commercially available Al2O3 feedstock material, AMDRY 6062, Oerlikon Metco, Kelsterbach, Germany, with particle size distribution of −45 + 22 µm was used. The process parameters are listed in Table 2. The particle mass flow rate of a focal plane from a HiWatch image denoted as \(\dot{m}\) was calculated based on Eq 11, where \(\rho_{p}\) is particle density, \(D\) particle diameter, \(v\) particle velocity, \(n\) denotes the number of particles in an image and \(L\) represents the measuring length of the camera in the spray direction.
The spatial distribution of the in-flight particle mass flow rates was determined through summation of the calculated \(\dot{m}\) values of the different focal planes. Please refer to (Ref 28) for further details of the measurement and validation of the particle mass flow rate in plasma jet. As the next step to determine LDE, the cumulative deposition profile of the impacted particles, referred to as footprint, was generated as a reference to investigate the deposited mass on the substrate. The same segmentation as for the free jet transverse section was conducted on the height profile of the footprint, see Fig. 7(a). The mass of the deposited feedstock material on each segmented element on the substrate was estimated based on the volume of each element and the density of the feedstock material with zero porosity assumption. Please refer to (Ref 27) for further details regarding the determination of LDE. Figure 7(b) shows the interpolated distribution of the calculated LDE in the entire free jet. Through this methodology, the in-flight particle properties in each element can be allocated to the corresponding LDE values. The resulted data sets are used for the development of the ANFIS model to predict DE based on the particle properties.
(a) Segmented height profile of the experimental footprint under laser-scanning microscope and (b) spatial distribution of LDE in the entire free jet according to (Ref 27). Reprinted from Surface and Coatings Technology, Vol. 399, K. Bobzin, W. Wietheger, H. Heinemann, and S.R. Dokhanchi, Determination of local deposition efficiency based on in-flight particle diagnostics in plasma spraying, pg. 126,118, Copyright 2020, with permission from Elsevier
Results and Discussion
This section begins with the results of the first subsystem, namely the SVM models, for predicting the in-flight particle properties from process parameters. Subsequently, the results of the aforementioned data augmentation technique before training the ANFIS model are introduced. Finally, the findings of the second subsystem, namely the ANFIS model, to predict DE from particle properties using the SVM results are presented and discussed.
SVM Models
In the first subsystem of the introduced expert system, the in-flight particle properties are predicted by the SVM models. As described earlier, the SVM models are trained based on simulations of the plasma jet with different process parameters. To present the results of the expert system, the process parameters listed in Table 2 are considered at a spray distance of y = 100 mm. Figure 8 shows the results of the average particle temperatures and velocities for SVM, simulation and the corresponding experimental measurements. The comparison of the average particle properties confirms the previous validation of the simulation models and shows the accurate replication of the simulation data with SVM. The developed SVM models can predict mean particle velocities with R-squared of \(R_{{{\text{sq}},v}} \approx 0,97\) and mean particle temperatures with \(R_{{{\text{sq}},T}} \approx 0,82\), indicating more accuracy in prediction of particle velocities. The aforementioned prediction accuracies were calculated based on the mean particle temperatures and velocities of 45 individual simulations (Ref 16).
Results of the mean particle properties for experiment, simulation and SVM using the process parameters listed in Table 2
Data Augmentation
The amount of training data needed for developing an ANFIS model can be smaller than that required for training a classical neural network. Nevertheless, the training data size for ANFIS should be large enough to cover all possible cases, depending on the number of premise and consequent parameters (Ref 29). As Jang stated in (Ref 22), the amount and quality of data is a significant factor for the learning mechanisms applied to the determination of the membership functions. In this study, to improve the automated fine-tuning of the membership functions, the 100 available experimental data sets of particle properties and LDE are augmented with the factor of 1.5 prior to the training of the ANFIS model. As a result, 150 data sets in total are utilized to train the ANFIS model. The k-nearest neighbor (k-NN) technique is used for data augmentation, where k is set to 5. This method finds the k closest, most similar, neighbors to the sample point being investigated, by minimizing a distance function. For this purpose, the Euclidean distance (Ref 30) is considered based on Eq 12
where \(X\) and \(Y\) are two input vectors, one typically from original data and the other an input vector to be classified, \(I\) and \(L\) are the lengths of the vectors \(X\) and \(Y\), respectively, and \(J\) is the total number of features. In this study, the features of the input vectors are the particle temperatures, velocities and sizes, therefore \(J\) is equal to 3. To implement the k-NN method, at first 50 initial data sets of particle properties are created randomly in the oriented bounding box (OBB) of the original data, see Fig. 9(a). OBB is the box with the smallest dimension, in our case a volume, circumscribing all the points in the input space (Ref 31). In the next step, the five nearest original data to these initial sample data are determined based on Eq 12. The final augmented data result from the average of the nearest neighbors, see Fig. 9(b). In Fig. 9(b), one exemplary initial point is linked to its nearest neighbors with black dashed lines and to its final resulting k-NN point with a green line. Furthermore, to compare the distances between the points, the particle properties in this figure are normalized.
In the same way, the LDE of the generated data sets of particle properties are calculated by averaging the LDE of the corresponding nearest neighbors of original data. Figure 10 shows the overall data sets, including the augmented and original data, exemplarily in a 2D plot of temperature versus velocity, where the corresponding LDE values are given in color map. The overall data sets are used to develop the ANFIS model.
ANFIS Model
The ANFIS model to predict DE from particle properties is developed in the MATLAB environment. The total 150 data sets are divided into two unique groups, in a way that 80% of the data are used as training data and the remaining 20% as test data. This results in 120 data sets for training and 30 data sets for testing. To best model the data behavior using a minimum number of rules, the input–output training data are clustered beforehand using Fuzzy c-means (FCM) clustering technique (Ref 32). Using this method, multidimensional data points can be classified into a certain number of different clusters. Each data point in FCM belongs to a cluster to some degree that is specified by a membership grade. FCM starts with an initial estimate for the cluster centers that are intended to represent the mean location of each cluster. In addition, FCM provides each data point with a membership grade for each cluster. Subsequently, FCM shifts the cluster centers to the optimal location within a data set by iteratively updating the cluster centers and the membership grades for each data point. FCM clustering allows minimum number of rules in an ANFIS model, as the rules partition themselves according to the fuzzy qualities associated with each of the data clusters. In this study, the training data are classified into four clusters and the information returned by FCM is used to generate a Sugeno-type ANFIS model, in a way that membership functions represent the fuzzy qualities of each cluster. Figure 11(a) shows the block diagram of the developed ANFIS. The Sugeno-type inference system contains four rules corresponding to the four pre-defined clusters. The inputs of the model include particle temperatures, velocities and sizes, while DE is its single output. Each input is described by one Gaussian MF per each fuzzy cluster, resulting in four MF for each input, and the output variable has one linear MF per each fuzzy cluster. The membership functions of the inputs are presented in Fig. 11(b).
In the following, the results of the developed ANFIS model in the second subsystem of the expert system are presented. Figure 12 shows the predicted LDE versus their experimental targets for the 30 test data sets. Each test index in this figure represents a combination of particle properties. The average particle temperatures \(\overline{{T_{p} }}\), velocities \(\overline{{v_{p} }}\) and sizes \(\overline{{D_{p} }}\) of the test cases with their corresponding experimental local deposition efficiencies \({\text{LDE}}_{{{\text{exp}}}}\) and predicted values \({\text{LDE}}_{{{\text{ANFIS}}}}\) are listed in Table 3. The ANFIS model is able to predict LDE accurately with root-mean-square error (RMSE) of about 1.1%. The results show that the deposition efficiency has a general tendency to increase with increasing particle size, velocity and temperature, while this behavior is nonlinear. It is also evident that this nonlinearity is well analyzed by the ANFIS for the typical range of particle properties in APS. The particles with relatively larger diameters have greater momentum, which leads to a deeper penetration into the plasma jet. Furthermore, the cascaded design of the three-cathode plasma gun allows larger particles to stay in the high temperature core of the plasma jet (Ref 18), contributing positively to both their melting ratio and velocity to achieve the best DE in the free jet.
The results of the mean particle properties predicted by the SVM models in the first subsystem are fed into the ANFIS model to predict the global DE. The bar chart shown in Fig. 13 makes a comparison between the predicted DE and the measured DE for the case of process parameters listed in Table 2. The experimental measurements for determination of DE are taken based on the norm, by weighing the substrate before and after coating with respect to the mass of the sprayed material during the coating process. The result of the predicted DE is in a good agreement with the corresponding experimental target. This demonstrates the proof of concept that the developed expert system is capable of predicting the global DE based on the norm, while being trained with spatially resolved deposition efficiency on the substrate. This confirms the motivation of using LDE to fine-tune such an expert system, while providing that much experimental data for the global DE is barely practical.
Comparison of the experimental DE and its corresponding predicted DE by ANFIS using the SVM results for the process parameters listed in Table 2
Conclusions and Outlook
Deposition efficiency (DE), as a key performance indicator in plasma spraying, depends on several intrinsic and extrinsic influencing variables. Increasing DE has always been a difficult task in the process development of plasma spraying because of the nonlinear and complicated interdependencies of the influencing factors. This study aimed to overcome these difficulties by developing an expert system to predict DE using modern AI methods. The developed expert system consists of two subsystems: one for predicting particle properties from process parameters using a support-vector machine and another for predicting DE from particle properties using an adaptive neuro-fuzzy inference system. The following conclusions can be drawn from the presented results:
-
Demonstration of proof of concept to predict global deposition efficiency from spatially resolved deposition efficiency on the substrate
-
High prediction accuracy of the developed expert system to predict DE with RMSE of about 1.1% by combination of ANFIS and SVM models
-
The results revealed that DE tends to rise with increasing particle size, velocity, and temperature, whereas this behavior is nonlinear. It should be pointed out that the DE may depend also on other parameters, such as powder feed rate, torch traverse velocity or spraying distance in general.
-
Contribution to the acceleration of the coating development process in APS using the developed expert system
The developed expert system can be used as a tool to adjust the process parameters to produce sustainable and cost-effective coatings. Future works could be focused to create an iterative feedback loop based on experimental data sets to boost the prediction accuracy of the system. In this regard, the developed expert system can also help to build experimental training data with DEs greater than 50%. Furthermore, this work serves as a good starting point to perform real-time data analysis to finally achieve the complementary concept of Digital Shadow in plasma spraying.
Change history
24 May 2023
A Correction to this paper has been published: https://doi.org/10.1007/s11666-023-01602-5
Abbreviations
- AI:
-
Artificial intelligence
- ANFIS:
-
Adaptive neuro-fuzzy inference system
- ANN:
-
Artificial neural network
- CFD:
-
Computational fluid dynamics
- DE:
-
Deposition efficiency
- DoE:
-
Design of experiment
- FCM:
-
Fuzzy c-means
- FIS:
-
Fuzzy inference system
- FL:
-
Fuzzy logic
- k-NN:
-
K-nearest neighbor
- LDE:
-
Local deposition efficiency
- LSE:
-
Least squares estimation
- MF:
-
Membership function
- OBB:
-
Oriented bounding box
- RMSE:
-
Root-mean-square error
- SVM:
-
Support-vector machine
References
A. Vardelle, C. Moreau, N.J. Themelis, and C. Chazelas, A Perspective on Plasma Spray Technology, Plasma Chem. Plasma Process, 2015, 35(3), p 491-509.
G. Mauer, K.-H. Rauwald, R. Mücke, and R. Vaßen, Monitoring and Improving the Reliability of Plasma Spray Processes, J. Therm. Spray Tech., 2017, 26(5), p 799-810.
K.E. Schneider et al. Thermal Spraying for Power Generation Components (John Wiley & Sons, 2006)
J. Richter, Entwicklung Einer Prozessregelung Für Das Atmosphärische Plasmaspritzen Zur Kompensation Elektrodenverschleißbedingter Effekte. Ilmenau, Technische Universität, Dissertation, 2013, Universitätsverlag Ilmenau, 2014 (in ger)
K. Seemann, Vorhersage Von Prozess- und Schichtcharakteristiken beim Atmosphärischen Plasmaspritzen mittels statistischer Modelle und Neuronaler Netze, Aachen, Technische Hochschule, Dissertation, 2005, 1st ed., Mainz, 2005 (in ger)
F.B.G. Ernst, Qualitätskontrolle auf Basis Optischer Prozessdiagnostik Und Neuronaler Netze Beim Thermischen Spritzen, Aachen, Technische Hochschule, Dissertation, 2007, Shaker, 2007 (in ger)
S. Guessasma, G. Montavon, P. Gougeon, and C. Coddet, Designing Expert System Using Neural Computation in View of the Control of Plasma Spray Processes, Mater. Design, 2003, 24(7), p 497-502.
A.-F. Kanta, G. Montavon, M. Vardelle, M.-P. Planche, C.C. Berndt, and C. Coddet, Artificial Neural Networks Versus Fuzzy Logic: Simple Tools to Predict and Control Complex Processes—Application to Plasma Spray Processes, J. Therm. Spray Tech., 2008, 17(3), p 365-376.
A.-F. Kanta, G. Montavon, C.C. Berndt, M.-P. Planche, and C. Coddet, Intelligent System For Prediction and Control: Application in Plasma Spray Process, Expert Syst. Appl., 2011, 38(1), p 260-271.
T. Liu, M.P. Planche, A.F. Kanta, S. Deng, G. Montavon, K. Deng, and Z.M. Ren, Plasma Spray Process Operating Parameters Optimization Based on Artificial Intelligence, Plasma Chem. Plasma Process, 2013, 33(5), p 1025-1041.
A.H. Pakseresht, E. Ghasali, M. Nejati, K. Shirvanimoghaddam, A.H. Javadi, and R. Teimouri, Development Empirical-Intelligent Relationship Between Plasma Spray Parameters and Coating Performance of Yttria-Stabilized Zirconia, Int. J. Adv. Manuf. Technol., 2015, 76(5-8), p 1031-1045.
S. Datta, D.K. Pratihar, and P.P. Bandyopadhyay, Hierarchical Adaptive Neuro-Fuzzy Inference Systems Trained By Evolutionary Algorithms to Model Plasma Spray Coating Process, J. Intell. Fuzzy Syst., 2013, 24(2), p 355-362.
Z. Wu, Empirical Modeling For Processing Parameters’ Effects on Coating Properties in Plasma Spraying Process, J. Manuf. Process., 2015, 19(5566), p 1-13.
M. Awad and R. Khanna, in Support Vector Regression. Efficient Learning Machines (Apress, Berkeley, CA, 2015)
C.M. Bishop, Pattern Recognition and Machine Learning, 1st ed. Springer, New York, 2016.
K. Bobzin, W. Wietheger, H. Heinemann, S.R. Dokhanchi, M. Rom, and G. Visconti, Prediction of Particle Properties in Plasma Spraying Based on Machine Learning, J. Therm. Spray Tech., 2021, 30(7), p 1751-1764.
M. Öte, Understanding Multi-Arc Plasma Spraying, Dissertation, 2016, RWTH Aachen University, Shaker Verlag
K. Bobzin and M. Öte, Modeling Multi-Arc Spraying Systems, J. Therm. Spray Tech., 2016, 25(5), p 920-932.
K. Bobzin, M. Öte, J. Schein, S. Zimmermann, K. Möhwald, and C. Lummer, Modelling the Plasma Jet in Multi-Arc Plasma Spraying, J. Therm. Spray Tech., 2016, 25(6), p 1111-1126.
L.A. Zadeh, Fuzzy Sets, Inf. Control, 1965, 8(3), p 338-353.
M.-D. Jean, B.-T. Lin, and J.-H. Chou, Design of a Fuzzy Logic Approach Based on Genetic Algorithms For Robust Plasma-Sprayed Zirconia Depositions, Acta Mater., 2007, 55(6), p 1985-1997.
J.-S. Jang, Anfis: Adaptive-Network-Based Fuzzy Inference System, IEEE Trans. Syst. Man Cybern., 1993, 23(3), p 665-685.
C.C. Lee, Fuzzy Logic in Control Systems: Fuzzy Logic Controller I, IEEE Trans. Syst. Man Cybern., 1990, 20(2), p 404-418.
E.H. Mamdani and S. Assilian, An Experiment in Linguistic Synthesis With a Fuzzy Logic Controller, Int. J. Man-Mach. Studies, 1975, 7(1), p 1-13.
T. Takagi and M. Sugeno, Fuzzy Identification of Systems and Its Applications to Modeling and Control, IEEE Trans. Syst. Man Cybern., 1985, SMC-15(1), p 116-132.
A. Hamam, N.D. Georganas, A Comparison of Mamdani and Sugeno Fuzzy Inference Systems For Evaluating the Quality of Experience of Hapto-Audio-Visual Applications. in 2008 IEEE International Workshop on Haptic Audio Visual Environments and Games, 18.10.2008 - 19.10.2008 (Ottawa, ON, Canada), IEEE, 2008-2008, p 87-92
K. Bobzin, W. Wietheger, H. Heinemann, and S.R. Dokhanchi, Determination of Local Deposition Efficiency Based on In-Flight Particle Diagnostics in Plasma Spraying, Surf. Coat. Technol., 2020, 399, p 126118.
K. Bobzin, W. Wietheger, M.A. Knoch, and S.R. Dokhanchi, Estimation of Particle Mass Flow Rate in Free Jet Using In-Flight Particle Diagnostics in Plasma Spraying, J. Therm. Spray Tech., 2020, 29(5), p 921-931.
A. Al-Hmouz, J. Shen, R. Al-Hmouz, and J. Yan, Modeling and Simulation of an Adaptive Neuro-Fuzzy Inference System (ANFIS) for Mobile Learning, IEEE Trans. Learn. Technol., 2012, 5(3), p 226-237.
L. Peterson, K-Nearest Neighbor, Scholarpedia, 2009, 4(2), p 1883.
J. O’Rourke, Finding Minimal Enclosing Boxes, Int. J. Comput. Inf. Sci., 1985, 14(3), p 183-199.
J.C. Bezdek, R. Ehrlich, and W. Full, Fcm: the Fuzzy C-Means Clustering Algorithm, Comput. Geosci., 1984, 10(2-3), p 191-203.
Acknowledgments
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC-2023 Internet of Production—390621612. Simulations were performed with computing resources granted by RWTH Aachen University under project rwth0570.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: When originally published, the HTML version of the article did not include the special issue tagline. The special issue tagline has been added to the HTML version of the article.
This article is an invited paper selected from presentations at the 2022 International Thermal Spray Conference, held May 4-6, 2022 in Vienna, Austria, and has been expanded from the original presentation. The issue was organized by André McDonald, University of Alberta (Lead Editor); Yuk-Chiu Lau, General Electric Power; Fardad Azarmi, North Dakota State University; Filofteia-Laura Toma, Fraunhofer Institute for Material and Beam Technology; Heli Koivuluoto, Tampere University; Jan Cizek, Institute of Plasma Physics, Czech Academy of Sciences; Emine Bakan, Forschungszentrum Jülich GmbH; Šárka Houdková, University of West Bohemia; and Hua Li, Ningbo Institute of Materials Technology and Engineering, CAS.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bobzin, K., Heinemann, H. & Dokhanchi, S.R. Development of an Expert System for Prediction of Deposition Efficiency in Plasma Spraying. J Therm Spray Tech 32, 643–656 (2023). https://doi.org/10.1007/s11666-022-01494-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11666-022-01494-x