Introduction

Cermet coatings like WC-Co and Cr3C2-NiCr are frequently applied to protect highly stressed surfaces against wear, mostly by means of high-velocity oxygen-fuel spraying processes (HVOF) (Ref 1, 2).

Comparisons of different spraying powders with respect to their in-flight particle behavior and the corresponding coating characteristics are found in a number of studies. Nahvi and Jafari (2016, Ref 3) compare the standard WC-Co powder to WC-FeCrAl and WC-NiMoCrFeCo with respect to microstructural and mechanical properties like porosity and hardness. Varis et al. (2014, Ref 4) investigated the formation mechanisms, the structure and coating properties of HVOF-sprayed WC-CoCr coatings considering the in-flight particle properties in relation to process conditions as well as their influence on the coating properties using first-order process maps. Kuroda et al. (2001, Ref 5) analyze the effect of powder sizes and pressure of combustion chamber on particle temperature, velocity, and the resulting residual stress of the coating surface. However, in these studies the spraying parameters of the HVOF process are set to fixed sets of few values, which differ for each powder.

This study is an attempt to compare different powders over the same range of parameter values based on the same experimental design for all powders. A review on design of experiments in thermal spaying is given in Pierlot et al. (2008, Ref 6). WC-Co powders of different average particle sizes have been compared using the Taguchi experimental design in Lovelock (Ref 7). Preceding screening experiments identified kerosene flow rate (K), spray distance (D; distance of the spray gun to the specimen), feeder disc velocity (FDV) and lambda (L) (ratio of actual oxygen–kerosene ratio to stoichiometry, i.e., lean mixtures with oxygen excess have L>1) as parameters with a relevant influence on the in-flight particle behavior as well as on the coating properties (Ref 8).

In this study, Cr3C2-NiCr and three different WC-based powders are compared over settings of four process parameters (K, D, FDV, L). The effects of these parameters on properties of the coatings are studied with the aid of generalized linear models (Ref 9, 10). Measured are the coating hardness, porosity and thickness as well as the deposition efficiency of the coating process. A further insight into the relationship between the different powders/process settings and coating properties is gained by measuring the in-flight particle properties such as the particle velocity and the particle temperature.

Experimental Procedure

Powder Feedstock

In this study, a WC-Co 88/12 powder of type WOKA 3102 from Oerlikon Metco (WC-Co), WC-FeCrAl 85/15 powder of type Amperit 618.074 from H.C. Starck (WC-FeCrAl), a WC-Co 88/12 test powder with 100-nm carbides from H.C. Starck (WC-Co-100 nm) and a Cr3C2-25 (Ni20Cr) powder of type WOKA 7302 from Oerlikon Metco (Cr3C2-NiCr) were used for spraying, and the results were compared. The choice of powder was made to investigate the influence of different spray parameters and powders of different compositions. The focus was on the common WC-based powder with different carbides sizes, as well as an alternative WC-FeCrAl powder with a different matrix and a Cr3C2-NiCr powder for comparison. Figure 1 shows SEM images of cross sections of the powders used in this study.

Fig. 1
figure 1

Cross section of the used feedstock powder (a) WC-Co, (b) WC-Co-100 nm, (c) WC-FeCrAl and (d) Cr3C2-NiCr; (mag.: 500x)

Full size image

In the cross section, it can be seen that all feedstock powders have nearly similar porosity, which was determined analogous to the porosity of the coatings by means of image evaluation software. The corresponding porosity values are shown in Table 1.

Table 1 Parameters d10, d50 and d90 of the volumetric particle size distribution as well as the porosity of the feedstock powder
Full size table

Additionally, the particle size distribution was determined by laser diffraction analyzer S3500 by Microtrac Inc. (Montgomeryville, USA). According to the manufacturer information, all feedstock powders have a particle size of − 45 + 15 µm.

As shown by laser light scattering, the used feedstock features a uniform volumetric particle size distribution (Fig. 2). The parameters d10, d50 and d90 of the monomodal size distribution of each powder are given in Table 1, where, e.g., the parameter d50 corresponds to the median particle size.

Fig. 2
figure 2

Particle size distribution of the used WC-Co, WC-Co-100 nm, WC-FeCrAl and Cr3C2-NiCr powder

Full size image

In order to minimize agglomeration effects, all powders were heated up to 100 °C in an oven for 1 h and afterward homogenized in a tumbling mixer for 15 min

Coating Process and Experimental Setup

All experiments were conducted using a Wokajet 400 HVOF system from Oerlikon Metco with a TWIN 120AH powder feeder system. For the coating experiments, EXXSOL D 60 kerosene (ExxonMobil Chemical Central Europe GmbH, Germany) was used as a liquid fuel.

The experimental setup included the HVOF spraying system, an in-flight particle measurement system, and a turning lathe. Ahead of the coating of the steel tubes, the spray gun was positioned in front of the Accuraspray g3 particle diagnostics system (Tecnar, Saint-Bruno, Quebec, Canada) whereby particle temperature and particle velocity were determined.

As substrate material, tubes made of C45 steel (1.0503) with an outer diameter of 50 mm (wall thickness 3 mm) and length of 100 mm were used. All samples were pretreated by means of grit blasting with corundum EKF 100 (particle size of 106-150 µm), a pressure of 4 bar, a distance of 100 mm and an angle of 45°. After the pretreatment, all steel tubes were cleaned with ethanol in an ultrasonic cleaner for 15 min and preheated at 100 °C afterward. The substrates were rotated by turning lathe to ensure an even coating on the outside of the tubes.

The spray gun was handled by an industrial robot of type IRB-4600 (ABB Ltd., Zurich, Switzerland). The handling parameters of the spray gun and the turning lathe were kept constant and are summarized in Table 2.

Table 2 Handling parameters of the spray gun
Full size table

During the coating experiments, the insides of the specimen were constantly cooled with compressed air.

Coating Characterization

After the coating process, the samples were metallurgically analyzed. For this purpose, cross sections of the individual samples were created and scrutinized. For the hardness measurement, a hardness tester of the type M400 from LECO (St. Joseph, Michigan, USA) was used. The hardness (H) was determined according to Vickers (HV 0.3). The measurements of the coating thickness (Th) as well as the porosity (P) were taken with a light microscope type BX51M by Olympus (Hamburg, Germany) as well as an FE-SEM with secondary electron (SE) and backscattered electron (BSE) detectors, type JSM-7001F (JEOL, Germany).

The deposition efficiency (De, in %) was determined based on the differential weights of the samples before and after the coating process in relation to the amount of powder delivered during the time the spray gun remained on the surface of the sample, i.e., it is computed via the formula

$${\text{De}} = \frac{{M_{{{\text{spec}},2}} - M_{{{\text{spec}},1}} }}{{M_{{{\text{sprayed}}}} }} = \frac{{M_{{{\text{spec}},2}} - M_{{{\text{spec}},1}} }}{f \cdot t}.$$

Here \(M_{{{\text{spec}},2}}\) and \(M_{{{\text{spec}},1}}\) denote the mass of the specimen after and before spraying, respectively. \(f\) is the feeder rate in \({\text{g}}/\min\) and \(t = 75.39\sec\) is the spraying time over the sample. The feeder rates were determined by gravimetric measurements (three repetitions) for each powder (Table 3).

Table 3 Feeder rates \(f\) in g/min
Full size table

Table 4 summarizes all varied process parameters and the measured responses to the process parameters.

Table 4 Controllable and measured variables in the spray process
Full size table

Statistical Design of Experiment

In order to allow a systematic comparison of the in-flight powder behavior and the corresponding coating properties, a statistical design of experiment (Ref 11, 12) was employed. The four process parameters (kerosene flow, lambda, spray distance and feeder disc velocity) were varied on a high, middle and low value (coded as 1, 0 and − 1). Table 5 summarizes the values of the process parameters and their coding. Feeder disc velocity is measured in % of the maximal frequency of the feeder disc which is 10 cycles/min.

Table 5 Coded process parameters
Full size table

A full factorial design on all possible combinations of these three levels would amount to an unfeasible number of \({3}^{4}\)=81 experimental runs per powder, 324 runs altogether for all four powders. Instead, a \({2}^{4-1}\)-fractional factorial design with a double central point added for each powder results in ten runs per powder, 40 runs for all four powders. This design (Table 6) still allows for the fitting of main effect statistical models.

Table 6 Fractional factorial design with double center point
Full size table

Ideally, in a statistical design of experiment, the order of the experimental runs is random. However, due to the high time required for powder feedstock change and the accompanied cleaning process of the powder feeder, it is not practical to change the powder type after each run. To minimize the time for the exchange of the powder, the experimental design was blocked into eight blocks of five spraying experiments with the same powder. The experiments were run on two consecutive days with five runs per powder on each day. The order of the runs with each powder on day one (Cr3C2-NiCr, WC-Co, WC-Co-100 nm, WC-FeCrAl) was permuted as (WC-Co-100 nm, WC-FeCrAl, Cr3C2-NiCr, WC-Co) on the second day. On each day, one of the added central points was run such that they can be used to estimate the error as well as to check for possible day effects (Ref 13, 14).

Generalized Linear Models

In order to understand how the coating properties depend on the process parameters, statistical models for the responses hardness (H) and deposition efficiency (De) are fitted in dependence of the process parameters. It is expected that the coating properties are related to the particle properties in flight. Therefore, models for hardness and deposition efficiency were also built depending on the in-flight particle properties, i.e., temperature (T) and velocity (V). The in-flight properties themselves depend on the process parameters and are models for this dependencies are build, too. Figure 3 gives an overview of all three kinds of models considered.

Fig. 3
figure 3

Statistical models for coating and in-flight properties

Full size image

The models come from the class of generalized linear models (GLMs) (Ref 9, 10). As all response variables can only take positive values, a Gamma distribution is assumed, which also allows for higher varieties in distributional shape than the normal distribution, while still following the idea of a mean value around which observations are varying. GLMs for functional responses have been applied to an HVOF spraying process in (Ref 15). The mean value changes depending on the specific setting of the process parameters. Only main effects (no interactions or quadratic effects) are considered. The link function is always the identity. Therefore, the model for, for example, hardness (depending on process parameters) is similar to a linear model:

$$E\left( {{\text{Hardness}}| K, L, D, FDV} \right) \, = \beta_{0} + \beta_{1} K + \beta_{2} L + \beta_{3} D + \beta_{4} \cdot{\text{FDV}},$$

where β0, β1, β2, β3, β4 are unknown parameters estimated by maximum likelihood estimation and E(Hardness \(| K, L, D, FDV\)) denotes the expected value of hardness around which observed values vary for the specific setting \(\left(K, L, D, FDV\right)\). As a measure of goodness of fit, Nagelkerke’s \(R_{N}^{2}\) is used as an extension of the well-known \(R^{2}\) to generalized linear models (Ref 16).

Results and Discussion

This section shows the experimental results and discusses them based on statistical modeling.

Particle Velocity and Temperature

Figure 4 shows the results for the particle velocity. The observed values are plotted against the experimental settings. For each run, the parameter setting is stated in coded values below the plot, and the settings are ordered first according to descending spray distance, then according to kerosene, etc.

Fig. 4
figure 4

Experimental results for particle velocity vs parameter settings ordered according to descending spray distance and kerosene

Full size image

The WC-based powders show a similar behavior for the same parameter settings. The velocities of WC particles reach values between 530 m/s and 950 m/s. In contrast, the velocity of Cr3C2-NiCr particles is more sensitive to changes of the process parameters. Here the velocities vary between 200 and 1100 m/s. However, the variation of the process parameters results in a similar behavior of the Cr3C2-NiCr powder when compared to the WC-based powders. Only the level of the influence varies for the Cr3C2-NiCr powder. Since for each powder the same parameter settings were used, a different behavior of the in-flight particles must be due to different powder properties, such as density, matrix material and carbide size. Indeed, the greater sensitivity of the velocity for Cr3C2-NiCr particles can be explained by their smaller density and weight.

Figure 5 shows the results for the particle temperature of the different powders. As in Fig. 4, the observed values are plotted against the experimental settings. The experimental run 2 and run 6 were carried out as the center runs of the design of experiments on the two different days with the same process parameters. The values of the particle properties are rather similar for those runs with differences in the range of the measuring error of the measuring system.

Fig. 5
figure 5

Experimental results for the particle temperature vs parameter settings ordered according to descending spray distance and kerosene

Full size image

Again, the WC powders exhibit a similar behavior of the particle temperature for the same parameter settings. In contrast, the temperature of the Cr3C2-NiCr particles shows a different reaction. Whereas the particle temperature increases with a decreasing spray distance for WC powders, it decreases for Cr3C2-NiCr particles. To get a further insight into the effect of process parameters on the particle properties V and T main effect, GLMs are fitted. Table 7 and Table 8, respectively, summarize the results. Next to the estimated main effects, the values in brackets are p-values of Wald tests testing the submodel, defined by setting the effect of this parameter to zero, against the full model (Ref 9, 10). For all fitted models, the Nagelkerke \({R}_{N}^{2}\) values are high, indicated a good fit of the models.

Table 7 Main effect models for particle velocity [m/s]
Full size table
Table 8 Main effect models for particle temperature [°C]
Full size table

For velocity V, the two largest main effects are a positive effect of kerosene (K) and a negative effect for spray distance (D) for all four powders, i.e., the velocity increases with kerosene and decreases with spray distance within the considered range of parameters. More kerosene in the combustion leads to a faster gas jet, which by momentum transfer increases particle velocities. Theoretically, powder particle velocities increase, attain a maximum value and then decrease in the direction of the substrate (Ref 17). The range of the spray distances used in the experiments is such that the decreasing part of that curve is observed. This velocity drop is due to deceleration by air friction. Since the WC-based powder particles are heavier (higher density while same particle sizes) than the Cr3C2-NiCr particles, they are harder to accelerate and harder to decelerate.

For particle temperature, see Table 8, the two largest effects show a positive effect of kerosene and a negative effect for spray distance for all WC-based powders, while the direction of the effects is reversed for Cr3C2-NiCr. It is known from the literature that with a reduction of the spray distance, the dwell time of the spray particles in the hot gas jet is reduced, which results in insufficient heating of the particles and lower particle temperature (Ref 18, 19). Here it can be seen that only the Cr3C2-NiCr powder follows this trend, which can be explained by the thermal evolution of the particles during the spraying process. Note that spray distance is a nonlinear monotone approximation for time. Initially, the particles are heated until reaching their melting point. Then, during melting, as the latent heat of fusion is absorbed, the temperature remains constant. After melting, the particle temperature increases again in the flame up to its maximum value and then starts to decrease due to the drop in the gas jet temperature. The particle reaches solidification again and the temperature drops further—but usually the particle hits the substrate before the solidification point. In the case of the contrary behavior for the WC powders, it is assumed that the maximum temperature peak is already passed and the particle temperature decreases with an increasing spray distance. In this case, a decrease of the spray distance will prevent the particles from further cooling down during flight. In all runs but run 10 with \(\left(K, L, D, FDV\right)=(-1, 1, 1, -1)\) the particle temperatures are above the melting point of the cobalt matrix (1495 °C). The kerosene dependence may also be explained by the theoretical curve of the temperature over the distance. Hence, for higher kerosene values the temperature/distance curve is stretched and translated to the right. In particular, if a part of the curve that has a positive slope (as for Cr3C2-NiCr) is shifted to the right, lower temperatures for higher kerosene are obtained for certain distance values. The opposite happens for phases of the curve with a negative slope (as for WC-based powders). The observed Cr3C2-NiCr particle temperatures are all above the melting point for the NiCr-matrix (about 1400 °C). For 3 runs, we even observe temperatures above the melting point of Cr3C2 (1895 °C). However, it is known from the literature that especially in oxygen-rich flames (lambda greater than (1) the high heat impulse can also lead to negative effects such as strong oxidation of the matrix material (Ref 20, 21) or other undesirable phase transformations (Ref 1). In Ni-20%Cr coatings, for example, an exothermic reaction has been demonstrated that leads to in-flight oxidation of the particles, further increasing the particle temperature. This means that the particles become hotter the longer they remain in the hot spray jet or the further they move away from the core of the flame, which is due to the interaction with the entrained air and the oxygen it contains (Ref 21).

Coating Properties

Hardness and Porosity

The measurements of Vickers hardness are in a range of 1000 HV0.3-1400 HV0.3 for WC-based coatings. According to the literature, this is the common hardness range for HVOF-sprayed, WC-based coatings (Ref 1, 14). However, deviations were noticeable in the results due to the parameter variations. The results of experimental run 1 (coded parameters: − 1, − 1, 1, 1) show low hardness values of 720 HV0.3 to 820 HV0.3 depending on the powder. This value will be discussed below looking also at the porosity of the coating.

To investigate the relationships between coating hardness and the process parameters, main effect plots were prepared. The main effect plot in Fig. 6 displays the dependence of hardness on the four process parameters. Observed values of hardness are plotted against the settings of the process parameters.

Fig. 6
figure 6

Main effect plots for hardness

Full size image

By the chosen experimental design, the effect of individual process parameters on the hardness becomes visible in the difference between mean values on the high and low settings, which are connected by lines in the main effect plot. Estimates of the parameters in the corresponding main effect generalized linear model are obtained as displayed in Table 9.

Table 9 Main effect models for hardness [HV 0.3]
Full size table

The main effect plot (Fig. 6) as well as the models (Table 9) support the following results. For all four powders, kerosene and spray distance have a significant effect on the response variable hardness—with kerosene having a positive effect and spray distance having a negative effect, which were also the main contributing effects on particle velocity. Indeed, statistical modeling of hardness in dependence of particle velocity and particle temperature reveals the particle velocity as the main contributing effect (Table 10).

Table 10 Main effect models for hardness [HV 0.3] depending on particle properties
Full size table

The dependence of the hardness on the velocity is plausible, because the higher the velocity of the particles hitting the surface, the harder the coating becomes. When the particles hit the substrate, the kinetic energy of the spray particles is converted into deformation and heat energy. The conversion into heat energy leads to additional melting of the particles and thus to a higher degree of melting. Due to the higher degree of melting, the particles deform more when deposited on the substrate or on already deposited splats, which leads to a better superposition and bonding of the splats with each other (Ref 22). After impact and deformation on the surface, the thermal energy is transferred to the substrate, leading to solidification of the splat particles and successive formation of the coating.

On the one hand, a higher kerosene content leads to a higher pressure in the combustion chamber, which ultimately results in a higher kinetic energy of the spray particles. As a result, the spray particles hit the substrate surface with a higher kinetic energy and degree of melting, deform and deposit on the surface to form the coating. Due to the higher kinetic energy and the associated greater plastic deformation of the splats, the superposition of these same splats is significantly affected, resulting in a higher hardness. At a lower particle velocity, the degree of deformation of the particles is lower, resulting in poorer superposition and bonding between the particles. This poorer superposition and bonding of the particles can lead to pores during successive coating formation and thus negatively influence the hardness of the coating.

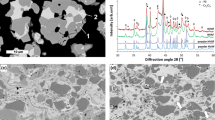
However, the impact of subsequent spray particles can also lead to additional impact hardening and post-compaction of the previously deposited layers (peening effect) (Ref 23). Figure 7 displays the influence of the particle velocity and the resulting lower porosity in a cross section of the coatings deposited with Cr3C2-NiCr powder for two different parameter settings.

Fig. 7
figure 7

Cross section of the coatings obtained of Cr3C2-NiCr powder for two different parameter settings in two different magnification stages (mag.: 100x—left side; mag.: 500 x—right side): (a) + (b) experimental run 1; (c) + (d) experimental run 9)

Full size image

Figure 7 shows cross sections of coatings produced with Cr3C2-NiCr powder in two test runs once with high particle temperature at simultaneously low particle velocity (Fig. 7a + b) and with high particle velocity at comparatively low particle temperature (Fig. 7c + d).

The image clearly shows that the coating thickness in experimental run 9 is significantly higher in comparison with experimental run 1, which also corresponds to the lower deposition efficiency. A possible reason for this could be that the low deposition efficiency at high particle temperatures in the case of Cr3C2-NiCr is at least partly due to the evaporation of Cr (or the formation of volatile CrO3). Indeed, a tendency for Cr3C2-rich particles to rebound has been noted in some work (Ref 24, 25). Image analysis of the magnified SEM images indicates a higher volume fraction of Cr3C2 in experimental run 1, which could contribute to the loss of the NiCr matrix (either by direct evaporation of Cr or formation of volatile CrO3). This will be investigated in more depth in further studies.

Nevertheless, as shown in Fig. 7, the coating deposited with a low particle velocity (Fig. 7b) within experimental run 1 exhibits a higher porosity than the coating deposited in experimental run 9 with a significant higher particle velocity (Fig. 7d). Hence, the particles in experimental run 9 were more strongly accelerated in the gas jet and thus have a higher velocity. The higher kinetic energy of the particles leads into a better deformation of the splats when hitting the surface of the substrate or the previously deposited coating layer and thus leads to denser coatings, which in turn leads to a higher hardness of the coatings. Here, a negative correlation between porosity and hardness can be observed. Table 11 provides the Pearson correlation coefficients between hardness and porosity, which confirms this effect.

Table 11 Pearson correlation coefficients between hardness and porosity
Full size table

Considering the negative Pearson correlation between porosity and hardness, the low hardness results for experimental run 1 (coded: − 1, − 1, 1, 1) can be explained due to higher porosity values. Figure 8 shows cross sections of the three WC-based powders in this experimental run in different magnification stages.

Fig. 8
figure 8

Cross sections of the coatings obtained in experimental run 1 of different WC-based powders with two different magnification stages (mag.: 100x—left side; mag.: 500 x—right side)

Full size image

The cross sections show that the interface is characterized by a gap-free bonding of each coating to the substrates. Nevertheless, the coatings also show increased porosity. The measured particle velocity of this experimental run is low for all powders. Due to the low particle velocity, the kinetic energy of the impinging particles is low. Due to the lower kinetic energy, the associated plastic deformation of the splats is weaker, leading to insufficient superposition of the splats, which leads to an increased porosity in the coatings (Ref 1, 26,28,28) and thus to low hardness. The cross sections in Fig. 8 show that in particular the WC-Co-100 nm and the WC-FeCrAl coatings also exhibit an increased porosity at the transition of the coating to the embedding resin. This shows that the coatings undergo post-compression due to subsequently impinging splats (peening effect). In this area of the coating, no additional compaction took place due to the absence of another pass with the spray gun and thus no splats impinging at the surface, which explains the increased porosity and confirms the peening effect.

Deposition Efficiency and Coating Thickness

The experimental results for deposition efficiency are displayed in Fig. 9. The observed values are again plotted against the experimental settings. For each run, the parameter setting is stated in coded values below the plot, and the parameters are ordered first according to descending kerosene, then according to descending lambda, etc.

Fig. 9
figure 9

Experimental results for deposition efficiency

Full size image

For Cr3C2-NiCr, all experiments showed a significantly lower deposition efficiency than for powders based on WC, which exhibit similar deposition efficiencies. These runs with extremely low deposition efficiency for Cr3C2-NiCr also exhibit extremely high particle temperatures—even above the melting point of Cr3C2. This indicates that the range of parameters used in this study is not optimized for Cr3C2-NiCr.

The highest deposition efficiencies are achieved for WC-Co-100 nm for certain parameter settings ( − 1, 1, − 1, 1). In order to compare the influence of process parameters, again main effect GLMs are deployed.

As shown in Table 12, kerosene is the main contributing effect and has a negative influence for the WC-based powders, but a positive influence for the Cr3C2-NiCr powder. This means, in case of the WC-based powders, that an increase in the kerosene flow leads to a decrease in the deposition efficiency, while it increases for Cr3C2-NiCr. High lambda values, i.e., lean mixtures, have always a negative effect on deposition efficiency. The sign of the effect of spray distance is reversed to that of kerosene for all powders. This indicates the importance of the particle velocity for the effect on deposition efficiency. Modeling deposition efficiency as function of the particle temperature and velocity (Table 13) reveals that the particle velocity becomes the main contributing effect for all three WC-based powders with a negative sign.

Table 12 Main effect models for deposition efficiency [%]
Full size table
Table 13 Main effect models for deposition efficiency [%] depending on particle properties
Full size table

The negative sign indicates that by increasing the particle velocity the deposition efficiency decreases. The decrease of deposition efficiency with increasing velocity may be explained by a higher probability of rebounding of particles with high velocity. Due to their high velocity, the dwell time of the particles in the hot gas jet decreases leading to a lack of heat transfer to the particles and subsequently to more particles that are not or only partly melted. These particles cannot be sufficiently deformed and embedded on the substrate surface, bounce off the substrate surface and thus do not form a coating. It can be assumed that the particle velocity and the resulting energy are not sufficient to deform the particles in a similar way to cold spray technology to ensure sufficient adhesion. Compared with the cold gas technique, the critical velocity required for this was not reached or exceeded, and the particles bounce off the substrate surface.

In addition to the deposition efficiency, the influence of the process parameters on the resulting coating thickness was also investigated in this study. The main effect plot in Fig. 10 displays the dependence of thickness on the four process parameters.

Fig. 10
figure 10

Main effect plot for thickness

Full size image

It is evident that only feeder disc velocity has a large positive effect on the coating thickness. This proportional relationship is already well known and investigated. Thus, a higher powder feeder rate leads to higher coating thicknesses, since more powder material is available, which is applied to the substrate surface.

Conclusion

  • Coatings manufactured by a HVOF thermal spray process using four different powders,

  • WC-Co, WC-Co-100 nm, WC-FeCrAl and Cr3C2-NiCr were compared with respect to in-flight particle properties (particle temperature and particle velocity) as well as coating properties (hardness, deposition efficiency, porosity and thickness) for several combinations of process parameter. Using statistical design of experiments, a suitably adapted fractional factorial design enabled the comparison of the influence of the process parameters on the in-flight particle properties as well as the coating properties. All powders were sprayed with the same spraying device and the same parameter settings.

  • The particle velocity increases with higher kerosene flow rates and a smaller spray distance, most pronounced for Cr3C2-NiCr powder.

  • The two largest effects on particle temperature are a positive impact of kerosene and a negative impact of spray distance for all WC-based powders, while with reversed impact on Cr3C2-NiCr.

  • Within the considered parameter range, the results showed huge differences in the hardness of the respective coatings. In particular, the hardness of the WC-based coatings reveals/yields hardness values above 1400 HV0.3. The coating hardness was mainly influenced by the particle velocity leading to a higher hardness with increasing particle velocity.

  • The coating hardness and porosity are negatively correlated. Thus, it could be shown that a coating with a low porosity has a higher hardness than a coating with a higher porosity.

  • Within the parameter range, the deposition efficiency decreases with increasing particle velocity. Due to a lower dwell time of the particles in the hot spray jet and thus a lower melting degree, there is a higher probability of rebounding of particles with high particle velocity.

  • Highest deposition efficiencies are achieved for WC-Co-100 nm.

  • The thickness results can be explained very well by the conversion of mass during the coating process. A higher feeder rate results in more powder in the gas jet, which leads to a higher coating thickness. It is assumed that the relation \(thickness\) ∼ \(deposition efficiency\cdot feeder disc velocity\) displays the density of the coatings by the slope of the lines of the fitted generalized linear models with identity link and gamma distribution.