Numerical and Experimental Analysis of the Deformation Behavior of CoCrFeNiMn High Entropy Alloy Particles onto Various Substrates During Cold Spraying

Abstract

The bonding mechanisms of a wide range of metallic materials in cold spraying have been studied, mainly attributed to adiabatic shear instability (ASI) at high strain rates, whereas the impact and deformation behavior of high entropy alloys (HEAs) onto various substrates has not been widely explored. HEAs have been characterized by excellent strain-hardening ability and high resistance to shear localization, which can influence their bonding mechanism during cold spray. In this study, experimental and numerical analyses of single-particle impact behavior during cold spraying of CoCrFeNiMn onto commercially pure aluminum (CP Al), aluminum alloy (Al6082), stainless steel (SS304), and titanium alloy (Ti6Al4V) substrates were carried out. The impact morphology revealed ASI in the HEA particle, and SS304 and Ti6Al4V substrates. The HEA/SS304 pair showed a higher critical velocity compared to HEA/Ti6Al4V due to the lower density and thermal conductivity of Ti6Al4V compared to SS304. Mechanical interlocking was observed on CP Al and Al6082 substrates and was attributed to the localized deformation of the substrates. An empirical equation showed this is influenced by the particle density and substrate hardness. This work critically evaluates and provides a better understanding of HEA particle–substrates deformation behavior, expanding its applicability to a wider range of substrates.

Introduction

A new class of metallic alloys that have attracted much attention and interest recently from both the scientific and industrial communities are the high entropy alloys (HEAs). This is because of their unique properties, which are believed to surpass those of conventional alloys. HEAs are constructed with five or more principal elements with equiatomic or near-equiatomic proportions and thus derive their performances from multi-principal elements rather than a single element (Ref 1,2,3). In addition, most HEAs have been characterized to form single-phase solid solutions, particularly the equiatomic Cantor alloy—CoCrFeNiMn (Ref 2). This HEA has received extensive attention due to its excellent strength-ductility combination at cryogenic temperatures and high fracture toughness (Ref 4), oxidation-resistance (Ref 5, 6), wear-resistance (Ref 7) and corrosion resistance (Ref 8).

Recently, due to the unique properties of the Cantor alloy, its applications as a coating are emerging, such as to improve the surface properties of materials for industrial applications like bond coats in thermal barrier coatings (TBCs) (Ref 9), and other extreme high-temperature and environmental conditions. Most of the techniques for developing HEA coatings are fusion-based techniques such as laser cladding (Ref 10, 11), magnetron sputtering (Ref 12), and thermal spraying technologies such as plasma spraying (Ref 13) and high-velocity oxy-fuel spraying (Ref 14). These technologies, however, have been reported to result in deleterious effects such as in-flight oxidation, phase transformation and elemental segregation resulting from melting and solidification of the HEA feedstock powder (Ref 15). To prevent these effects, it is, therefore, important to employ low-temperature, non-fusion-based technologies such as cold spraying for developing HEAs coatings.

Cold spraying (also known as cold gas dynamic spraying) is a materials deposition technique, with solid powder particles (typically, 5-100 µm in diameter) accelerated in a jet of compressed gas (which can be nitrogen, air or helium) to high velocities ranging from 300 to 1400 m/s, through a converging-diverging (De Laval) nozzle (Ref 16, 17). Coatings are formed in the cold spray process through plastic deformation (at a high strain rate) of the sprayed feedstock material, bonding to the substrate upon impact. This occurs at temperatures below the material melting point (solid-state) and sufficiently high impact velocity. Being the cold spray process a supersonic particle deposition method, it largely relies on the kinetic energy of the feedstock material, providing a means of manufacturing HEA coatings with desirable microstructures, mechanical properties, and applications that thermal spray technologies could not achieve. However, the impact behavior and bonding mechanism of cold spraying of HEAs such as CoCrFeNiMn have not been widely explored.

There are several experimental investigations and numerical analyses published in the past decades on the impact and deformation behavior of materials and the bonding mechanisms in cold spraying, which is still a matter of debate. Impact-induced bonding mechanisms in cold spraying of metallic materials are broadly classified as metallurgical bonding (Ref 18, 19), mechanical interlocking (Ref 7, 19) and material intermixing at low deposition efficiency (Ref 20, 21). Metallurgical bonding has been attributed to metal jetting, associated with ASI (Ref 18, 22) or shock (pressure)-wave release mechanism (Ref 23). Mechanical interlocking occurs when impacting particles are trapped or embedded (or anchored) within the substrates or coating materials. This happens when the particle is heavier and harder than the substrate material. Material intermixing at the particle–substrate interface occurs under low deposition efficiency, where most of the spraying particles rebound causing severe plastic deformation of the first deposited layer of the particle–substrate material and subsequently, the formation of vortex-like intermixing interfaces. The particle must have a sufficiently high density and hardness than the substrate material for material intermixing to occur (Ref 21).

The prevailing hypothesis (ASI) for metallurgical bonding (where the particle and substrate materials have similar compositions and/or properties such as density and hardness) is that when a particle impacts with a substrate, extensive localized high strain-rate plastic deformation occurs at the interface due to dynamic shearing load. At this high shearing strain, plastic strain energy dissipated as heat increases causing thermal softening of the materials, which dominates over-strain-hardening and a reduction in the flow stress. This can result in the formation of a jet-type outflow of material at the impact zone, which can help disrupt thin surface oxide films and enables an intimate contact of fresh metal–metal interfaces resulting in bonding (Ref 18, 22, 24). Generally, there exists a critical velocity for a given material at a given temperature and particle size, such that the transition from erosion of the substrate surface to deposition of sprayed particles would occur (Ref 24). The particle velocity resulting from the onset of shear localization instability (ASI) is referred to as the critical velocity (Ref 18, 24, 25). Since the cold spray process is a high strain rate plastic deformation process, it is desirable to understand the impact and deformation behavior of the Cantor alloy and to predict its critical velocity onto various substrates.

Due to the transient nonlinear dynamic and contact nature of the cold spray process, the interactions between particles and of particles with a substrate are very challenging to analyze experimentally. Although post-mortem microstructural and micro-analytical examinations have been performed using several techniques, different computational tools have been employed in investigating the impact behavior of particles and substrates in the cold spray process, with several authors discussing how different spraying parameters influence this behavior. The different particle deformation modeling methods mainly include the Lagrangian method, Eulerian method, the Coupled Thermal-mechanical/Hydrodynamic (CTH) code and the Smoothed Particle Hydrodynamics (SPH) method (Ref 26, 27). Although the Lagrangian method is associated with extreme mesh distortion at the impact region, it is the first and most commonly used numerical method for cold spray (Ref 18). Its advantage is computational efficiency, and it facilitates the treatment of complex material models such as history-dependent material constitutive relations (Ref 26).

Important is the material model employed in predicting the plastic deformation behavior of materials in those computational tools. Several material models and their modifications (that fit well into experimental data) have been employed in modeling material behavior in cold spray. For instance, a range of material models including the Johnson–Cook (JC) model was studied by Rahmati and Ghaei (Ref 28), who reported that the accuracy of predicting impact morphology in cold spraying is largely influenced by the material model. Although the JC model is likely not to accurately predict the plastic deformation behavior of materials at strain rates above 10⁴ s^-1, it is still the material model often used to simulate particle deformation in cold spray, and it is readily available in most commercial finite element modeling packages.

The impact and deformation mechanism of CoCrFeNiMn onto various substrates with the cold spraying process was reported recently by Nikbakht et al. (Ref 29). Their studies revealed deformation twinning and FCC–HCP phase transformation features within the cold sprayed CoCrFeNiMn splat, which is attributed to the high strain-hardening rate of the alloy material. In their work, the deposition of the HEA with different particle sizes onto various substrates (Nickel, Inconel 625, and stainless steel 304) showed impact morphology that is strain-rate dependent in addition to being materials and microstructure dependent. It was observed that the HEA had the highest critical shear strain for strain localization compared to the substrate materials. This is due to the excellent strain hardening and moderate thermal softening of the CoCrFeNiMn, which can postpone shear localization (Ref 29, 30). From the perspective of cold spray, where materials deform at a strain rate of about 10⁹ s⁻¹, shear localization and instability are prominent, with thermal softening dominating over-strain hardening. Consequently, bonding of the particle to the substrates would occur. Materials such as CoCrFeNiMn with high critical shear strain for strain localization would require a high critical velocity for bonding in cold spraying (Ref 29). However, the numerical deformation modeling of the HEA, which can reveal the onset of shear localization and critical velocity for bonding of the HEA onto various substrates, was not studied in their work.

The impact and deformation behavior of a wide range of materials in cold spraying have been investigated, such as copper, nickel, titanium and aluminum (Ref 18, 31,32,33,34,35) onto various substrates materials, with similar and dissimilar materials combinations revealing distinct deformation behavior. Experimental and numerical analyses of the impact and deformation behavior of CoCrFeNiMn HEA onto various substrates would provide useful insight into the particle–substrates interactions, the onset of adiabatic shear instability and critical velocity for deposition during cold spraying. Therefore, experimental and numerical analyses of single-particle impact behavior of CoCrFeNiMn onto aluminum, aluminum alloy (Al6082), AISI 304 stainless steel (SS304), and titanium alloy (Ti6Al4V) substrates were investigated in this study.

Methodology

Materials and Experimental Procedure

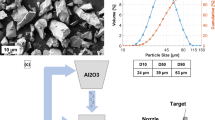
Spherical gas atomized CoCrFeNiMn HEA powder from HC Starck Surface Technology & Ceramic Powders GmbH (Goslar, Germany) was used as feedstock material for this study. Figure 1(a) and (b) shows the HEA feedstock powder particles’ surface morphology, obtained using scanning electron microscopy (SEM), with an FEI (The Netherlands) XL30 equipped with Secondary (SE) and Back Scattered Electron (BSE) detectors. The SEM was operating at an accelerating voltage of 20 kV and a working distance of 10 mm. Most of the particles are spherical, with some satellite particles present. Also, the dendritic grain structure is observed (Fig. 1b). The particle size distribution (displayed in Fig. 1c) was obtained using laser diffractometry (Horiba LA-960, Horiba Scientific, Japan). The particle size distribution was determined to a mean of Dv50 = 25.53 µm, Dv10 = 16.38 µm, and Dv90 = 41 µm, respectively. Since the experimental mean particle diameter, Dv50 = 25.53 µm, a particle diameter of 25 µm was employed for the numerical modeling.

Fig. 1

SE SEM surface morphology of the CoCrFeNiMn HEA powder (a), magnified BSE micrograph of a single HEA particle, and particle size distribution of the HEA feedstock powder (c)

The elemental composition of the HEA feedstock powder presented in Table 1 was evaluated with Energy-dispersive x-ray spectroscopy (EDX) (Oxford Instruments, UK) mounted on the SEM. The elemental composition indicates an equiatomic HEA composition. The x-ray diffraction (XRD) spectrum shown in Fig. 2 reveals that the HEA powder contains only FCC single phase. This was conducted on a D8 Advance da Vinci x-ray Diffractometer (Bruker, Germany), with a wavelength of 0.15406 nm (Cu-K_α), in Bragg Brentano θ-2θ geometry, from 20° to 80° 2θ, with a 0.02° step and 0.1 s dwell time.

Table 1 Elemental composition of CoCrFeNiMn HEA powder

Fig. 2

XRD diffractogram of the HEA powder

The feedstock powder material was cold sprayed onto four different substrates: commercially pure aluminum (CP Al), aluminum 6082 (Al6082), Ti6Al4V (Ti64) and AISI 304 stainless steel (SS304) substrates. The Al6082 substrate was chosen for its high strength in comparison with CP Al, however; Al6082 and CP Al are grouped as soft substrates, while the Ti64 and SS304 are grouped as hard substrates. Regarding the chemical composition (wt.%) of the soft substrates, CP Al is 0.09 % Fe, 0.32 % Si, 0.02 % Zn and balance Al, and Al6082 is 0.36 % Mg, 0.27 % Si, 0.04 % Ti, 0.12 % Mn, 0.02 % Fe, Cr and Zn, 0.03 5 Cu, the remainder being Al. Regarding the hard substrates chemical compositions (wt.%), Ti64 is 6.54 % Al, 4.13 % V, 0.02 % Si, 0.01 % Mn, 0.03 % Mo, 0.05 % Fe, 0.04 % Nb and Ti to balance, and SS304 is 19.0 % Cr, 9.3 % Ni, 0.05 % C and Fe to balance.

Single particles were sprayed onto the four substrates using the so-called wipe test, in which a mirror-polished substrate is moved rapidly through the spray jet. This can be achieved by adjusting the powder feed rates (low powder feed rate) and spraying at a high traverse speed (Ref 33). The wipe-test experiments were performed using a high-pressure cold spray system at the University of Nottingham. The cold spray nozzle used was hardened stainless steel, designed with an area expansion ratio of 8 and a divergent length of 150 mm. The nozzle was held stationary while the substrates were mounted on a programmable x-y table that allowed a controllable scan pattern and velocity. To obtain a wide range of particle velocities, nitrogen (N₂) and helium (He) were used as accelerating gas. The powder carrier gas (N₂) pressure was set at a pressure of 0.1 MPa higher than the accelerating gas pressure. The spraying parameters used for the wipe-test are presented in Table 2.

Table 2 Cold spraying process parameters

The single-particle impact wipe-test samples were cold mounted in EpoFin^® epoxy resin (Struers, UK) and subsequently ground using P240, P400, P800, P1200 and P4000 grinding papers. After grinding, samples were polished using 1 µm diamond paste, and thereafter, a mirror-polished surface was obtained using a colloidal silica suspension. All samples were washed and cleaned with ethanol at every subsequent grinding and polishing step. The cross sections of the single-particle impact tests were examined using the SEM.

The microhardness analysis of the mirror-polished substrates and HEA feedstock powder particles samples are presented in Table 3. This was performed using a Wilson VH3100 Vickers Microhardness instrument (Buehler, USA). Each mounted substrate and powder particles sample underwent ten measurements. A 500-gf load was applied on the substrate samples, whereas a 10-gf load was applied on the powder sample, using a dwell time of 15 s. The final value is presented as an average with standard error. Depending on the processing conditions and grain size, the microhardness of bulk Cantor alloy from literature ranges from 140-350 HV (Ref 36, 37). The deviation in the microhardness of the HEA powder can be attributed to the powder particle displacement in the resin during the microhardness test, which would likely affect the accuracy of the measurement. From cold spraying of CoCrFeNiMn powder, the microhardness of 124 HV (Ref 7) and 176 HV (Ref 29) have been reported, which is close to the hardness of the SS304 (192 HV). The difference can be attributed to the applied load, grain and particle size, microstructure, and processing condition. In this case, we can assume that the HEA and SS304 have little difference in their material properties.

Table 3 Microhardness of HEA powder and substrates

Computational Procedure

To determine the feedstock particle velocities and temperatures before impact on the substrates, following the experimental impact conditions as stated in Table 2, a Computational Fluid Dynamics (CFD) model was employed using the commercial code of Fluent (version 2020). Based on the experimental conditions and nozzle dimensions, a 2D CFD axisymmetric (the CFD model set-up is shown schematically in Fig. 3a) analysis was conducted, meshed with a grid of quadrilateral elements, using a realizable k—ε turbulent model with standard wall functions for the gas flow single-phase solution, while the particles are injected into the nozzle using a discrete phase model which considers the cold spray powder particles as a discrete entity moving through the gas phase (Ref 38, 39). Spherical CoCrFeNiMn particles of 25 µm, corresponding to the experimental mean particle diameter, with an initial temperature of 25 °C were used as powders injected at the nozzle inlet.

Fig. 3

Schematic representation of the CFD computation domain (a) and Abaqus model setup (b)

To investigate the HEA particle deformation behavior and predict the onset of deposition, the commercial explicit code, Abaqus/Explicit was used to perform a two-dimensional (2D) axisymmetric nonlinear, transient analysis of a high-velocity, single, micron-sized HEA particle impact in the Lagrangian frame of reference. Although, at large deformation and high strain rates, the Lagrangian approach has been reported to exhibit extremely severe element distortions in the deformed regions, which could lead to an adverse effect on the accuracy and convergence of the numerical simulation. This approach is the first and most used numerical simulation method in previous studies (Ref 18, 26). Nonetheless, the advantage of the Lagrangian approach is computational efficiency and it facilitates the treatment of complex material models such as history-dependent material constitutive relations.

The shape of the particle was assumed to be perfectly spherical. A normal impact of the particle on the substrate was assumed in the FEA model. Figure 3(b) shows a schematic representation of the FEA 2D model. The bottom of the substrate is fixed in all directions (U1 = U2 = U3 = 0) while a symmetry boundary condition (U1 = UR2 = UR3 = 0) is applied along the lateral edges (y-axis) of the substrate and particle. The substrate is modeled as a cylinder having a height and radius of 200 and 150 µm, respectively. This was done to ensure that the reflecting waves from the substrate bottom and far edges reach the impact zone only after the particle rebound.

The FEA analysis accounted for strain hardening, strain-rate hardening, thermal softening, and heating due to friction, plastic, and viscous dissipation. In this study, the heating was assumed to be adiabatic (Ref 18); nevertheless, 90% of the kinetic energy of the model was assumed to dissipate into heat allowing for some heat transfer and stored energy. The friction coefficient between the particle and substrate was assumed as 0.3 for all cases. A surface-to-surface penalty contact algorithm with balanced master-slave weighting was used, and the model meshed with four-node bilinear axisymmetric quadrilateral elements with reduced integration and hourglass control (CAX4R). To obtain accurate simulation results, a mesh convergence study was performed where mesh size at the particle–substrate impact region was varied until there was a negligible difference in the maximum interface temperature with further refinement of the mesh (Fig. 4). In addition, further refinement of the mesh is likely to result in early termination of the simulation due to severe element distortion. A mesh size of 0.375 µm was used in further simulations and analyses. It is worth noting that the mesh size in the substrate was decreased away from the impact zone to reduce the overall computational cost.

Fig. 4

Mesh convergence study, HEA/SS304 at 700 m/s. A mesh size of 0.375 µm was used for accurate simulation

The thermal response of the materials in the model was described by specific heat capacity. The elastic response was assumed to follow a linear elasticity defined by the elastic modulus and Poisson’s ratio. The plastic deformation behavior of the materials was defined using the JC plasticity model (Ref 40). The JC plasticity model of metallic materials is mostly applied to transient nonlinear dynamic simulations. The material is assumed to be an isotropic linear-elastic, strain-rate sensitive, strain-hardenable and thermally softenable plastic material (Ref 40, 41). The von Mises yield criterion states that the material starts to yield or flow when the von Mises stress reaches the material yield strength. As such, the JC plasticity constitutive model utilizes the J₂ yield function form of F (τ, ε), where F (τ, ε) = τ − Y (ε) and

$${\text{Y }}\left( \varepsilon \right) \, = \, \left[ {{\text{A }} + {\text{ B}}\varepsilon^{{\text{n}}} } \right] \, \left[ {{1 } + {\text{ CIn}}\left( {\varepsilon *} \right)} \right]\left[ {{1 } - \, \theta^{{\text{m}}} } \right]$$

(1)

Where τ is the equivalent shear stress and Y (ε) is the von Mises stress, and $\varepsilon^{*} = {\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {\mathop {\varepsilon_{0} }\limits }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop {\varepsilon_{0} }\limits }$}}$ , $\dot{\varepsilon }$ is the equivalent plastic strain rate, ε is the equivalent plastic strain, $\dot{\varepsilon }_{0}$ is the reference plastic strain rate, A is the yield strength (MPa) at zero-plastic strain and at room temperature, B is the strain hardening (MPa), n is the strain-hardening exponent, C is the strain rate constant, and m is the thermal softening exponent. Also, the temperature effect of the JC model given in the last part of Eq 1 account for the thermal softening of the material at a high strain rate, and θ is given as,

$$\theta = \frac{{T - T_{ref} }}{{T_{melt} - T_{ref} }}$$

(2)

where T is the homologous material temperature, T_ref is the reference temperature and T_melt is the material melting temperature. The increase in temperature T resulting from adiabatic temperature rise is given by Eq 3, where ρ is the material density, β is the inelastic heat fraction taken as 0.9 and C_p is the specific heat capacity of the material.

$$T = T_{ref} + \frac{\beta }{{\rho C_{p} }}\mathop \smallint \limits_{0}^{\varepsilon } Y\left( \varepsilon \right)d\varepsilon$$

(3)

Experimental Results of HEA Particle Impact on Various Substrates

The CoCrFeNiMn HEA feedstock powder material was deposited onto four different substrates grouped based on microhardness values presented in Table 3. SS304 and Ti64 substrates are grouped as hard substrates due to their greater microhardness, whereas CP Al and Al6082 are grouped as soft substrates due to their lower microhardness value. The substrate characteristics would reveal the distinct deformation behavior of the HEA during cold spraying.

Deformation Morphologies of HEA Particles on Hard Substrates

Figure 5 shows the top surface micrographs of impacted HEA particles on SS304 and Ti64 substrates, sprayed with impact conditions Run 1 (N₂; P_gas = 2.8 MPa and T_gas = 525 °C), Run 2 (N₂; P_gas = 3.3 MPa and T_gas = 525 °C) and Run 3 (He; P_gas = 3.3 MPa and T_gas = 400 °C). An overview at low magnification demonstrates that less than 30 % of impacting HEA particles adhere to the surface of the substrates at sprayed conditions, in Run 1. A slight increase in the number of adhered particles is observed when sprayed with impact condition Run 2. In cold spraying, a low bond ratio (or deposition efficiency) suggests that most of the particles are deposited at impact velocity below their critical velocity, and consequently, more craters (resulting from particle rebound) are formed on the substrate surface. The influence of the substrate on the deposition of HEA is observed when comparing the number of adhered particles on the surface of the substrate from the low magnification micrographs. There are a higher number of adhered particles on Ti64 than on SS304 substrate. At impact condition Run 3, more than 95% of impacting HEA particles adhere to the substrates’ surfaces.

Fig. 5

Low magnification SE SEM micrographs of wipe test samples of HEA particles on SS304 (a, c, e) and Ti64 (b, d, f) substrates at spray impact conditions Run 1 (a, b), Run 2 (c, d) and Run 3 (e, f)

Higher magnification images (close-up view in Fig. 6) show bonded HEA particles at impact conditions Run 1, Run 2 and Run 3. Extensive jetting is observed around the impact region of bonded HEA particles on the substrates with sprayed impact condition Run 3.

Fig. 6

Close-up images of the SE SEM micrographs of HEA single-particle impact on SS304 (a, c, e) and Ti64 (b, d, f) substrates at spray impact conditions Run 1 (a, b), Run 2 (c, d) and Run 3 (e, f)

Furthermore, Fig. 7 shows the BSE cross-sectional images of the deformation morphologies of HEA particles on SS304 and Ti64 substrates. The images were taken for samples with a higher percentage of adhered particles (sprayed at impact conditions Run 2 and Run 3). Figure 8(a) and (b) (at impact condition Run 2) shows deformed (half-flattened) HEA particles with the substrates slightly deformed. In contrast, a different particle–substrate interaction is observed with sprayed impact condition Run 3 (Fig. 8c and d), where jetting can be seen around the impact zone of the particle on the substrate's surface, with an increase in the particle penetration into the substrate. The higher impact velocity resulting from the use of helium gas is likely to result in the formation of the jet-type material flow at the particle–substrate interface. We observed from the cross-sectional micrographs that smaller particles significantly deformed the substrate resulting in the jetting of the substrate, whereas larger particles deformed more than the substrate, and, in some cases, no jetting was observed on the substrate.

Fig. 7

BSE cross-sectional micrographs of HEA single-particle impact on SS304 (a, c) and Ti64 (b, d) substrates at spray impact conditions Run 2 (a, b), and Run 3 (c, d). The insert (e) shows a larger HEA particle that has deformed more than Ti64 substrate, the same as observed on SS304 substrate

Fig. 8

Low magnification SE SEM micrographs of wipe test samples of HEA particles on CP Al (a, c, e) and Al6082 (b, d, f) substrates at spray impact conditions Run 1 (a, b), Run 2 (c, d) and Run 3 (e, f)

The height and diameter of the bonded particles were determined from the cross-sectional images, and subsequently, the flattening ratio was evaluated. The flattening ratio, defined as the ratio of the splat width (W) to the original particle diameter (D₀), can be used to evaluate the extent of particle deformation. The original particle diameter was evaluated according to King and Jahedi (Ref 42) analysis, given as $D_{0 } = \sqrt[3]{{\left( {W^{2} h} \right){ }}}$ for the case where there is minimal particle deformation such as in impact condition R2. While for impact condition R3, where particle spreads over the substrate surface, D₀ is given as $D_{0} = \sqrt[3] {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}}(W^{2} h)}$, where h is the splat height. It is worthy to note that the flattening ratio value is inevitably associated with an error. This is because mechanically polished cross sections do not normally pass through the center of splats. The calculated flattening ratio of about 10 particles with different particle sizes of the HEA on the hard substrates is presented in Table 4. There is an increase in the flattening ratio as the spray conditions were changed from Run 2 to Run 3. In addition, the flattening ratio increases with the increase in substrate hardness.

Table 4 Flattening ratio (FR) of HEA particle on hard substrates sprayed at impact conditions Run 2 and Run 3

Deformation Morphologies of HEA Particles on Soft Substrates

Cold sprayed HEA particles onto the top surface CP Al and Al6082 substrates with spray conditions Run 1, Run 2 and Run 3 are shown in Figs. 9 and 10. The substrate surface of the CP Al shows a larger number of adhering particles when compared to that of the Al6082, at impact conditions Run 1 and Run 2. The higher strength of the precipitation-hardenable Al alloy compared to CP Al has resulted in the lower percentage of adhered HEA particles on the substrate surface at impact conditions Run 1 and Run 2. The transition from the rebound regime to deposition regime on the Al6082 substrate occurred at impact condition Run 3. Again, it is observed here that the substrate properties thus influence the deposition of HEA even in the case of hard/soft particle–substrate combination.

Fig. 9

Close-up images of the SE SEM micrographs of HEA single particle on CP Al (a, c, e) and Al6082 (b, d, f) substrates at spray impact conditions Run 1 (a, b), Run 2 (c, d) and Run 3 (e, f)

Fig. 10

BSE cross-sectional micrographs of HEA single particle on CP Al (a, b, c) and Al6082 (d) substrates at spray impact conditions Run 1 (a), Run 2 (b) and Run 3 (c, d). Images were taken on substrates with higher percentage adhered HEA particles. The arrow in c shows an embedded particle

A close-up view of the SEM micrographs (Fig. 9) and BSE cross-sectional images (Fig. 10) reveals that HEA particles mechanically interlock (or are trapped) in the substrates. The mechanical interlocking of hard particles on soft substrates has been reported by previous studies (Ref 19, 20, 43). This is the result of the extensive deformation of the soft substrate, with a likely less deformed particle. In addition, as the spray impact conditions change from Run 1-Run 3, the HEA particle penetration depth on the CP Al substrate increases (Fig. 10a, b, and c).

Assessment and Selection of the HEA JC Material Data

Literature shows limited HEA material data for the JC model, to the best of the authors' knowledge. This may be because the HEA material space has not been widely explored. The choice of the JC set of parameters for the HEA material is very important to accurately predict the deformation behavior of the material during cold spraying (Ref 44). In this study, we collected different sets of JC parameters for the CoCrFeNiMn HEA, and materials with similar composition and/or impact behavior from literature (for example, set_2 is for CoCrFeNi HEA and the strain-hardening value (B) for set_3 and set_4 is for Ti64). All these sets were then compared, based on their stress-strain evolutions, and flattening ratio—with the SEM micrographs (“Experimental Results of HEA Particle Impact on Various Substrates” section). The results and comparisons were linked to the sets of the JC parameters, and the most suited one to obtain accurate results was selected for further numerical modeling. The approach ensures that the JC parameters still maintain a physical basis (derived from testing) and a better fit could have been found using parameter optimization, but this is not the focus of the study, as this would lose the link to the JC experimental test data which already exist for the HEA material.

The evolution of the stresses for the different JC parameters sets (Table 5) is plotted in Fig. 11 at a temperature of 473 K and a strain rate of 10⁷ s^-1. Surprisingly, it is immediately noted that there is a large variation of the set_1 parameter from the other sets. This large variation can be attributed to the high strain-hardening exponent, n, and strain-rate sensitivity (or strain rate constant, C) value of the set_1 JC parameters. This leads to the assumption that the strain-hardening exponent and strain-rate sensitivity values play an important role in the deformation behavior of materials in the cold spray process when using the JC material model. The variations in the evolution of stresses plotted for sets 2-6 as shown in Fig. 11(b), can be attributed to the different values of parameters A and B. Literature has not shown the effect of different JC parameters on material deformation behavior during cold spraying, particularly for numerical modeling. Significant differences observed for the different JC parameters in this study gave an insight into the importance of JC parameters for predicting cold spray particle deformation.

Table 5 Sets of parameters of the Johnson-Cook material model for CoCrFeNiMn HEA (the reference strain rate, ε_ref was assumed to be equal to 1 where data was not found in the literature)

Fig. 11

Stress-strain curve of HEA JC parameter sets at temperature T = 473 K and strain-rate ε = 10⁷ 1/s. All the JC sets are plotted in (a) while (b) is without the set_1

The JC parameters from the sets provided in Table 5 were employed in the FEA modeling and were then compared to the SEM micrographs in “Experimental Results of HEA Particle Impact on Various Substrates” section. The assessment of the JC material data was performed for impact on hard substrates as there is no significant particle deformation of the HEA on soft substrates, as can be seen from “Experimental Results of HEA Particle Impact on Various Substrates” section.

To predict the particle impact velocity and temperature from the experimental conditions, CFD was employed. The particle velocity and temperature profile of a 25 µm HEA particle before impact on the substrates are shown in Fig. 12. The highest particle velocity is achieved with spray condition Run 3, where helium gas was used as the accelerating gas. This is expected as the use of helium gas to achieve higher particle velocity when compared to nitrogen has been well established (Ref 45), though at similar process conditions. The reason for this lies in the expression for local gas velocity (Ref 46), $v = \sqrt {{\raise0.7ex\hbox{${\gamma RT}$} \!\mathord{\left/ {\vphantom {{\gamma RT} {M_{w} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${M_{w} }$}}}$ where $\gamma$ is the ratio of the constant-pressure to the constant-volume specific heat, which is 1.66 for helium and 1.4 for nitrogen, R is the gas constant, T is the gas temperature and M_w is the molecular weight of the gas. The gas velocity correlates positively with $\sqrt {\left( {\gamma /M_{w} } \right)}$, which is higher for helium than nitrogen.

Fig. 12

CFD results of an HEA 25 μm particle velocities (a) and temperatures (b) at spray conditions Run 1-Run 3. The use of helium as accelerating gas (Run 1) has resulted to higher impact velocity when compared to that of nitrogen gas (Run 1 and Run 2)

The particle velocity of the HEA particle before impact on the substrates are about 598, 647 and 987 m/s for spray conditions Run 1, Run 2 and Run 3, respectively. Also, the particle temperature for spray conditions Run 1, Run 2 and Run 3 are given as 398, 398 and 367 °C, respectively. The particle temperature for spray conditions Run 1 and Run 2 are overlapping. This is because the gas preheating temperature for both conditions is the same (i.e., 525 °C). On the other hand, the particle temperature for spray condition Run 3 is lower than that of conditions Run 1 and Run 2. Since the CFD results are likely to deviate from the actual experimental particle velocity and temperature (Ref 38, 47, 48), initial particle velocity and temperature of 600 m/s and 200 °C (473 K) were employed for the JC material data assessment and development using the FEA deformation modeling, which correlates with the spray condition Run 2. The initial substrates temperature was set to 300 K.

Figures 13 and 14 shows the FEA deformation pattern, and plots of flattening ratio (i.e., splat width) of the different sets in Table 5, respectively, which was performed for the low-velocity regime (impact condition Run 2). Thereafter the most suited JC model that was selected was employed in predicting the deformation pattern at high impact regime where jetting was observed (impact condition Run 3). These Figs are introduced to help the analysis with the experimental reference. It can be seen that the JC material data from Park et al. (Ref 49) (set_1) shows the largest deviation in the deformation pattern from the experiment, illustrating that the particle is extremely harder than the substrates resulting in mechanical interlocking. This is attributed to its high strain-hardening exponent and strain-rate sensitivity values of the set_1 JC parameters. In addition, the deformation pattern of the JC material data of CoCrFeNi HEA (set_2) shows that the material has greater ductility than CoCrFeNiMn HEA (set_6). From the plots of the numerical flattening ratio (i.e., splat width) of the different sets of the HEA JC material data, a link can therefore clearly be made between set_6 JC parameters and the experimental results.

Fig. 13

Deformation pattern of different JC parameter sets of the HEA particle on SS304 (a) and Ti64 (b) substrates

Fig. 14

Numerical and experimental splat width of the JC sets of HEA on SS304 (a) and Ti64 (b) substrates. The experimental splat width is indicated by the vertical line

Table 6 provides the final JC material data for the HEA particle, and the substrates used for further computational analysis in this study. It can be seen from the table that the HEA material has the highest strain-hardening value of 1365 MPa amongst all the alloys. Excellent strain-hardening ability and moderate/low thermal softening have been reported for this HEA (Ref 29, 30, 50). The critical shear strain for shear localization of the HEA (~7) is higher than that of Ti64 (1-2) (Ref 50) and SS304 (~5) (Ref 29) alloys. This high strain-hardening ability and low thermal softening, and consequently, resistance to shear localization of the HEA, would influence its deformation behavior during cold spraying.

Table 6 The Johnson–Cook material data for CoCrFeNiMn HEA and substrates used in this study

Numerical Analysis of the HEA Particle Deformation Behavior

Deformation Behavior of HEA on Hard Substrates

Figure 15 shows the deformation pattern in a HEA particle during impact onto flat SS304 and Ti64 substrates, for velocities within the spray impact conditions Run 1-Run 3 (550-900 m/s). The particle and substrate temperatures were initially set as 473 K and 300 K, respectively. For all impact velocities, localized heating was observed at the particle–substrate interface, though this is more severe for the higher impact velocity. The Figures also show a change in the particle–substrate interaction from the low-velocity regime to the high-velocity regime, where a “nose-like” feature at the particle edge changed to a “lip-like” feature (jetting) at the particle–substrate interface at higher impact velocity.

Fig. 15

Deformation pattern of HEA particle on SS304 (a) and Ti64 (b) substrates at impact velocity ranging from 550-900 m/s, this is within the spray conditions Run 1-Run 3

To obtain a better understanding of the change in the particle–substrate interaction or localization of plastic strain, the strain profile for a critical element that undergoes the highest amount of deformation at the particle interface on SS304 and Ti64 substrates is plotted in Fig. 16. There is an abrupt change in the plastic strain evolution at particle velocity of 700 and 600 m/s on SS304 and Ti64 substrates, respectively. The abrupt change in the strain at those particle velocities could be the result of thermal softening of the material, dominating over-strain-hardening during severe plastic deformation, consequently resulting in a high strain value at that velocity. This phenomenon has been observed by several researchers in the simulation of cold spraying of metallic materials, for example, Assadi et al.(Ref 18).

Fig. 16

Plots of strain development of HEA particle at a critical element, on SS304 (a) and Ti64 (b) substrates for various impact velocities. There is a change in strain evolution with time indicating a plastic strain instability at impact velocity 700 and 600 m/s, respectively

A similar trend was observed in the strain evolution of a critical element at the SS304 and Ti64 substrates impact zone, shown in Fig. 17. The abrupt change in the strain evolution at the substrate surface during the high impact of a HEA particle is observed at about 800 and 700 m/s particle velocities on SS304 and Ti64 substrates, respectively. Notably, the particle velocity resulting in the abrupt change in strain evolution is higher in the HEA/SS304 pair compared to the HEA/Ti64 pair. The FE modeling reveals—as also revealed by the impact experiment (Fig. 7), the influence of the substrate material on the deposition of HEA. The substrates are deforming less compared to the particles, and this is revealed by the greater particle velocity at which transition in the strain evolution is observed for the substrates. This finding also agrees well with the work of Nikbakht et al.(Ref 29), where CoCrFeNiMn particle deformed more intensely than the Inconel 625 substrate (with a hardness value of 270 HV).

Fig. 17

Plots of strain development of a critical element on SS304 (a) and Ti64 (b) substrates impact zone for various impact velocities. There is a change in strain evolution with time indicating a plastic strain instability at impact velocity 800 and 700 m/s, respectively

Deformation Behavior of HEA on Soft Substrates

The FE modeling reveals deeply penetrated CP Al and Al6082 substrates with likely less deformed HEA particles, as shown in Fig. 18. The initial kinetic energy of the HEA particle is mostly dissipated into plastic deformation of the soft substrates. This mechanism of bonding is referred to as mechanical interlocking. This contrasts with previous cases where both the particle and substrates were deforming. Since we could not observe any obvious change in the trend of strain at a critical element at the interface for the hard/soft material combination, the temperature profiles of a critical element at the substrates impact zone that experiences the highest temperature were plotted, as shown in Fig. 19.

Fig. 18

Deformation pattern of HEA particle on CP Al (a) and Al6082 (b) substrates at impact velocity ranging from 400-700 m/s. The particle penetration depth increases as the particle velocity increases as well as the substrate deformation

Fig. 19

Plots of temperature development of a critical element on CP Al (a) and Al6082 (b) substrates impact zone for various impact velocities. There is a high heat-up rate for all impact velocities but the impact velocity producing the highest heat-up rate is suggested to be the deposition velocity

Previous numerical studies performed for Ti/Al reported an abrupt change of interface temperature at the soft Al substrate (Ref 34). No abrupt change or “transition point” of the strain development was observed, which was due to the very fast temperature rise to the melting point of Al substrate (Ref 34). We observed a similar trend from the numerical analysis of HEA on CP Al and Al6082 at all impact velocities shown in Fig. 19. Interestingly, the temperature evolution of the CP Al substrate at 550 m/s shows a distinguishable heat-up rate, which rises more sharply than that of other impact velocities. Although the heating rate at the interface of the CP Al substrate at all impact velocities is in the order of 10⁹ K/s, the highest degree of heating to the substrate melting point (which is determined by the slope of the temperature-time profile in the first 10 ns) was observed at 550 m/s. For instance, the calculated heating rate at 500, 550 and 700 m/s is 30 × 10⁹, 65 × 10⁹ and 16 × 10⁹ K/s, respectively. The fast temperature rise of the CP Al substrate at 550 m/s is likely to contribute to the bonding of the HEA particle on the substrate. Again, there is a decrease in the rate of heating of the particle velocity above 550 m/s, which may suggest a threshold for the deposition of HEA on the CP Al substrate. On the Al6082 substrate, on the other hand, the highest degree of heating was observed at 600 m/s with heating rate of 40 × 10⁹ K/s.

It is noteworthy that the interface temperature of the soft substrates reaches the melting point over the range of impact velocities, from 400 to 700 m/s. Using a 10% deviation (Ref 38, 47) of the CFD results from the actual experimental particle velocity, the particle velocities for spray conditions Run 1 and Run 2 would therefore be 538 and 583 m/s, respectively. This suggests that these velocities are below the threshold needed for HEA deposition on Al6082 substrate, which is evidenced by the SEM top surface images (Fig. 8). Therefore, the degree of heating up to the melting point of the soft side may be one of the factors contributing to the deposition of a hard particle on a soft substrate as reported by Bae et al.(Ref 34). We observed additional criteria for mechanical interlocking of a hard particle on a soft substrate, the particle penetration depth. Figure 20 shows a plot of the particle penetration depth, which is the vertical distance from the substrate top surface to the particle bottom within the substrate. There is a higher particle penetration depth of HEA on CP Al than on Al6082 substrate over the range of impact velocities. An equivalent penetration depth at 500 m/s on CP Al is achieved at 600 m/s on Al6082 substrate, despite the lower melting temperature of Al6082 when compared to CP Al. This indicates that penetration depth likely plays a significant role in the bonding of the hard HEA on the soft Al and Al 6082 substrate materials (i.e., hard/soft material combination).

Fig. 20

Measured penetration depth from the FE modeling of HEA particle impact on CP Al and Al6082 substrates. A penetration depth of about 19 μm on CP Al substrate at 500 m/s is achieved on Al6082 substrate at 600 m/s (indicated by the arrow)

Discussion

Impact Phenomena of HEA on Hard Substrates

It is clear from the results that the impact-induced bonding in cold spraying of HEA on hard and soft substrates can be grouped into metallurgical bonding and mechanical interlocking, respectively. These bonding mechanisms can be influenced by various factors such as plastic strain, depth and width of craters, which are in turn influenced by the particle velocity and material properties (substrate and particle). In cold spraying, adiabatic shear instability at the impacting particles and substrates interfaces have been the generally accepted phenomena accounting for metallurgical bonding of metallic materials (Ref 18). Adiabatic shear instability is characteristically associated with high strain rate deformation, which results from an abrupt change in strain evolution (Ref 18, 22). The abnormal change in strain can lead to thermal softening (dominating over-strain-hardening at high strain rate) of metals; here, the mechanism of deformation changes from plastic flow to viscous flow, and consequently, a jet-type of material flow. The impact velocity, which initiates abnormal change in the strain evolution, is referred to as the critical velocity (which is material-dependent) for bonding in cold spraying.

The determination of the critical velocity of HEAs onto various substrates by the conventional concept of adiabatic shear instability (Ref 18) has not been studied yet. Apart from the concept of adiabatic shear instability, pressure wave interactions have been proposed as another concept that involves the interaction of strong pressure waves with the expanding particle edge during deformation (Ref 23). The pressure-wave mechanism relates the critical velocity linearly to the bulk speed of sound of pure metals. While this can be true for some metals such as Cu, Nikbakht et al.(Ref 29) reported that this mechanism cannot be relied on to predict the deformation mechanism and/or critical velocity of CoCrFeNiMn HEAs and all other HEAs. ASI mechanism can, thus, be employed in predicting the deformation behavior and critical velocity of this HEA material during cold spraying. The accuracy of these concepts or models is, however, influenced by the approximations used (numerical methods—Lagrangian and Eulerian approach, meshing, etc.) and the material model employed. The JC material model and the Lagrangian approach used in this study is likely to overestimate the critical velocity value, the use of other material model and the Eulerian technique can be employed in future work.

The impact of HEA particles onto the hard substrates (SS304 and Ti64) reveals adiabatic shear instability (change in the strain evolution) at the particle and substrates interfaces. The abrupt change in the strain at the particle interface occurs at lower velocities compared to that on the substrates (Figs. 16 and 17). This is because most of the plastic energy is primarily dissipated in the HEA particle both at lower impact velocity (where more craters were formed resulting from rebounds—Fig. 5(a), (b), (c), and (d) and at higher impact velocity where adiabatic shear instability or metal jetting was observed at the particle–substrate interfaces. The substrate material properties and the HEA particle sizes were observed to influence the particle impact morphology, with smaller particles resulting in pronounced jetting and penetration of the substrates, whereas larger particle sizes deformed more intensely than the substrates (Fig. 7). This can be attributed to the dynamic effects of small particles (such as high viscous shear strength at the jetting region, high strain-hardening rate, and higher strength following the Hall–Petch hardening), which can hinder localized deformation, as stated by Schmidt et al. (Ref 24).

Despite the greater hardness and strain-hardening of Ti64 (315.0 ± 4.5 HV and 1092 MPa, respectively) compared to SS304 substrate (192.1 ± 1.7 HV and 802.5 MPa, respectively), critical velocity for the bonding of HEA on Ti64 (600-700 m/s) is lower than that on SS304 substrate (700-800 m/s). Considering significant or critical plastic deformation of the substrate (as suggested by Ichikawa and Ogawa (Ref 51) and Arabgol et al.(Ref 52)) for the determination of the critical velocity of the HEA on SS304 and Ti64, this would therefore be 700 and 800 m/s for a 25 μm particle size of the HEA, respectively. In addition, the calculated flattening ratio was found to increase as the substrate hardness increases—from 192 HV to 315 HV for SS304 and Ti64 substrate, respectively, as well as an increase in the particle velocity (from spray conditions Run 1-Run 3, Fig. 12). As the substrate hardness and particle velocity increase, a higher proportion of the kinetic energy of the impacting particles is used in deforming them—especially for larger particles, rather than the substrates.

One would speculate that the impact of the HEA particle on the harder Ti64 would require a higher critical velocity for adiabatic shear instability to occur earlier in the Ti64 substrate compared to on SS304 substrate, but this is not the case. The underlying mechanism for this behavior can be explained as follows: plastic deformation of the particle/substrate at high strain rates reduces the thermal diffusion distance, D_th (Ref 53). Thus, the bonding of the cold spraying process is determined by the degree of localized strain and thermal build-up during the deformation process. Quantifying the affected volume over which there is an adiabatic temperature rise, V_aff for SS304 and Ti64 substrates at an impact velocity of 600 m/s, by using V_aff = D_th × A_c (Ref 54), where A_c is the maximum contact area extracted from the FE modeling results. The maximum contact area of HEA/SS304 and HEA/Ti64 at 600 m/s is calculated to be 0.867×10^-6 μm² and 0.827×10^-6 μm², respectively. We calculate the thermal diffusion distance using $D_{th} = \sqrt {\frac{K}{{\rho C_{p} }} \times t_{r} }$, with K being the thermal conductivity, ρ is the density, C_p is the specific heat capacity, and the contact time or residence time, t_r of the particle on both substrates is given as ratio of the particle diameter to impact velocity, which is $\approx$ 42 ns. The calculated D_th is 330 nm and 432 nm, and the corresponding V_aff is 27.3 nm³ and 37.5 nm³ for Ti64 and SS304 substrates, respectively. In addition, the FEA analysis of the temperature rise shown in Fig. 15 reaches a higher temperature at the Ti64 substrate surface than on SS 304. Thus, the thermal diffusion distance indicates that the degree of interface shear straining and thermal build-up is more localized on the Ti64 substrate. This can be attributed to the lower density and thermal conductivity of Ti64 (4430 kg/m³ and 6.7 W/mK). Moreover, this is evidenced by the fraction of adhered particles on Ti64 at spray impact condition Run 2 (about 600 m/s), which is higher than that on SS304 substrate. The more localized adiabatic shear strain and temperature rise on Ti64 substrate is likely contributing to the lower critical velocity for the bonding of the HEA particle.

The higher critical velocity for the deposition of HEA/SS304, on the other hand, lies in the window of deposition for austenitic stainless-steel 316L and 304-700 to 1500 m/s (Ref 24, 55). Since CoCrFeNiMn HEA and SS304 have similar materials properties (density and elastic modulus—Table 6) and crystal structure (fcc), it is ideal for comparison of HEA particle-particle and particle–substrate interactions in cold spraying. Schmidt et al.(Ref 24) calculated a critical velocity of about 700 m/s for a 25 µm austenitic stainless-steel 316L particle on a similar substrate material, which correlates well with the calculated critical velocity for the 25 µm HEA particle on the austenitic stainless-steel substrate in this study. However, the sluggish diffusion effect, higher critical shear strain and yield strength of CoCrFeNiMn is likely to result in a higher critical velocity for the deposition of the HEA/HEA when compared to HEA/SS304 (Ref 29). In general, the CoCrFeNiMn lies in the regime of difficult-to-spray materials for the cold spray process, such as austenitic stainless steel, titanium, Inconel 718, and other advanced engineering superalloys as the CoCrFeNiMn HEA material lies in the window of deposition for cold spraying of these materials.

Impact Phenomena of HEA on Soft Substrates

Cold spraying of the HEA onto Al6082 resulted in a lower fraction of adhered particles and a larger number of craters on the surface when compared to CP Al substrates (Fig. 9). Even though the deposited particles do not show any evidence of jetting, a fraction of particles were deposited on the soft substrates. The deposition is due to the significant localized deformation of the substrates, which act as ‘anchoring mechanism’ (Ref 56), while the HEA particle shows no deformation due to its greater resistance to shear localization (Ref 30). This mechanism of bonding is referred to as mechanical interlocking.

The FE modeling reveals a special kind of adiabatic shear instability occurring in the soft substrates, where no abnormal change or transition was observed but rather a high heat-up rate, as shown in Fig. 19. This has also been observed by a previous study (Ref 34). As the impact velocity increases, the heating rate increases due to the increase in the rate of deformation of the soft substrates, resulting from energy dissipation. An anomalous temperature-time profile and calculated heating rates were, however, observed at higher impact velocities from 550 to 700 m/s (Fig. 19). The heating rates decrease at these impact velocities, just above the threshold velocity for deposition. These observations can be associated with the findings of Hassani et al.(Ref 54, 57), where an increase in the impact velocity above the adhesion velocity would result in a decrease in the solidification/heating time, and therefore, a melt-driven erosion and, subsequently rebound of the impacted particles. This effect is attributed to the short-time scales for adhesion at those velocities, that is, the residence time for the HEA particle at a velocity above 550 m/s is far lower than the solidification time (and/or heating time) of the heated volume material at the substrate interface. Since the time needed for the solidification of the heated material is not enough for bonding, together with the higher rebound energy above the threshold particle impact velocity (Ref 58), the particle is likely to rebound with no mechanical resistance from the soft substrate material. Above these impact velocities (above 550 m/s), one can speculate the velocity for the onset of erosion of the soft substrates by the impact of the HEA particle.

Most notably, strain-induced melting at the interface of the soft substrate is, though, revealed by the FEA results, there is likely a critical penetration depth that would allow for anchoring of the particle–mechanical interlocking. Moreover, the penetration depth was found to increase monotonically as the particle velocity increased (as shown in Fig. 20). This is due to a steadily increasing dissipation of the particle impact energy by the substrate deformation (Ref 33). The FE modeling results agree well with the single-impact experiment of HEA/soft substrates (Fig. 10).

The greater resistance of Al6082 to strain localization despite its low melting point has resulted in the shallower penetration depth when compared to CP Al. This can be attributed to its higher strain-hardening exponent (and yield strength) and strain-rate sensitivity values (Table 6). Therefore, the particle penetration depth could play a significant role in the deposition of the HEA particle on the soft substrates.

To relate the deep-impact particle penetration depth to an onset deposition velocity (critical velocity), an empirical projectile law by Eichelberger and Gehring (Ref 59) relates the crater volume (V, in m³) produced by micrometeoroid impact on spacecraft, which has been used in evaluating the interfacial mixing of Cu/Al (Ref 20). This is given by Eq 4:

$$V = \left( {\frac{{\left( {0.00004} \right)E}}{B}} \right)$$

(4)

where E is the particle impact energy and B is the substrate Brinell hardness number.

We substitute $E = 1/2\left( {4/3\pi r^{3} \rho } \right)V_{p}$ into Eq 4, where ρ is the particle density, r is the particle radius and V_p is the particle velocity. Also, assuming the crater volume V equals the penetration depth D times particle face area (πr²). Thus, Eq 4 becomes:

$$V = \left( {\pi r^{2} } \right)D = \frac{{\left( {0.00004} \right)\left( {1/2} \right)\left( {\rho 4/3\pi r^{3} } \right)V_{p}^{2} }}{B}$$

(5)

The penetration depth, D is then given as:

$$D = \left( {0.00004} \right)\left( {\frac{2\rho r}{3}} \right)\left( {\frac{{V_{p}^{2} }}{B}} \right)$$

(6)

If the Brinell hardness of the substrate is estimated from the HV value from Table 3, a 25 μm HEA particle on CP Al at 600 m/s would result in a penetration depth of about 27 μm, which agrees well with the experiment (26.4 μm) and simulation results (24.4 μm). If we, again, assume that the whole of the particle has been embedded within the substrate (i.e., D = 2r) at the onset of deposition, then the critical velocity for the deposition of the hard particle on soft substrates would be given as:

$$V_{p} = \sqrt {75000 \times \left( {\frac{B}{\rho }} \right)}$$

(7)

Equation 7 gives us a simple, empirical method to estimate the particle velocity needed for the first monolayer deposition of hard HEA particles on soft substrates. For a 25 μm CoCrFeNiMn alloy HEA particle, impact on the CP Al and Al6082 substrates gives critical velocities of about 563 and 618 m/s, respectively. This value also agrees well with the FE modeling result—550 and 600 m/s, respectively. These results suggest that a high heat-up rate to the substrate melting point and particle penetration depth should be evaluated to determine the critical velocity of a hard particle on a soft substrate (it is worth noting that this is only for the first monolayer deposition), which depends on the substrate hardness and particle density. During coating build-up, material intermixing of the HEA on the soft substrates may occur under low deposition efficiency (which would be investigated in the future), but the repetitive impact of rebounded particles must be allowed (Ref 21)—which is not the case in this single particle impact study.

Conclusions

The impact and deformation behavior in cold spraying of CoCrFeNiMn HEA onto various substrates has been investigated experimentally and numerically. Different sets of Johnson–Cook parameters for the CoCrFeNiMn HEA and materials with similar composition and/or impact behavior were collected from the literature. All the sets were then compared, based on their stress–strain evolutions, and with the SEM micrographs flattening ratio. The results and comparisons were linked to the sets of the Johnson–Cook parameters, and the most suited one to obtain accurate results was selected for further numerical modeling to investigate the deformation behavior of the HEA onto various substrates using Abaqus/explicit in the Lagrangian frame of reference. The following conclusions were drawn from the results obtained in this study.

• Cold spraying of CoCrFeNiMn HEA onto SS304 and Ti64 (hard substrates) results in adiabatic shear instability of the particle and substrates—metallurgical bonding; however, cold spraying of the HEA onto CP Al and Al6082 (soft substrates) results in significant localized deformation of the substrates—mechanical interlocking. The material properties of the hard substrates such as density and thermal conductivity influence the particle–substrate deformation behavior—metallurgical bonding, while the soft substrate hardness and particle density would influence the extent of mechanical interlocking (penetration depth) of the HEA particles.

• The abnormal change in strain, which indicates adiabatic shear instability (and jetting), was observed in the HEA particle and SS304 substrate at particle velocities of 700 and 800 m/s, respectively. On Ti64 substrate, on the other hand, adiabatic shear instability was observed in the particle and substrate at particle velocities of 600 and 700 m/s, respectively. The hard substrates influence the onset of adiabatic shear instability in the particle. This suggests that the deformation or strain evolution of the substrate should be considered in determining the critical velocity for bonding. Thus, the critical velocity of the HEA on SS304 and Ti64 substrates is 800 and 700 m/s, respectively. The lower critical velocity of the HEA on Ti64, though with higher hardness and strain-hardening than SS304 substrate, is attributed to its lower density and thermal conductivity.

• Numerical—FEA modeling reveals an abrupt temperature rise to the material melting point in the cold spraying of the HEA on CP Al and Al6082 substrates, with the fastest temperature rise observed at 550 and 600 m/s, respectively. The particle deeply penetrated the soft substrates, which is due to the localized deformation of the substrates.

• Particle penetration depth was reported as an additional criterion for the mechanical interlocking of the HEA particle on the soft substrates. An empirical equation relating the particle penetration depth to particle velocity shows that mechanical interlocking is influenced by the soft substrate hardness and particle density. With the empirical equation, the critical velocity of the HEA on CP Al and Al6082 is 563 and 618 m/s, respectively. The higher critical velocity of the HEA on Al6082 is attributed to its higher strength, strain-hardening exponent and strain-rate sensitivity when compared to CP Al.