Introduction

Nowadays, thermally sprayed ceramic coatings gained raised attention. Potential applications range from electrical components to high-temperature applications such as metal melt filtration. Their property profile is given through their unique lamellar microstructure, evincing numerous microcracks, amorphous zones, and pores, resulting from the thermal-spray process itself (Ref 1,2,3,4).

A key property to e.g. assess mechanical handling or thermal shock performance of ceramic components is the flexural strength. Within the characterisation of strength, the scatter of strength data represents a material property, whereas the scale of strength is related to the components’ geometry and size, hence, to the effectively stressed volume. Against this background, the analysis of strength data in terms of Weibull theory addresses the quantification of that scatter by the scatter parameter m, called Weibull modulus. Moreover, a scale parameter, the characteristic strength σ0, can be derived for the investigated effective specimen volume or effective surface area, respectively (Ref 5). The estimation of both is outlined in the European Standard EN 843-5 (2006).

Through literature review, a broad overview regarding the mechanical properties of free-standing thermally sprayed (more precisely flame-sprayed) alumina is provided (Ref 6,7,8). Recently, fracture mechanical properties were investigated, such as fracture toughness or R-curve behaviour. When compared to sintered alumina, the fracture toughness KIc was found lowered for flame-sprayed alumina (Ref 8). In agreement with that, a lowered strength was frequently reported for flame-sprayed Al2O3 as well, which is mainly attributed to the weakened microstructure (Ref 6,7,8). However, as shown by Aneziris et al. (Ref 7), the thermal shock performance of flame-sprayed alumina is superior compared to conventional oxidic ceramic products. By thermal shock experiments according to Hasselman (Ref 9, 10), critical temperature differences without strength degradation up to 800 K could be derived. In addition, a decrease in strength of about 40% only was reported for a temperature drop of about 1000 K. However, the determination of the Weibull parameters was not performed after thermal shocking. Back then, the Weibull modulus m prior to thermal shock amounted 4.7 (Ref 7). Key point of the presented research is the determination and comparison of the Weibull modulus m and σ0 before and after thermal shock. During industrial application though, e.g. as thermal barrier coatings, flame-sprayed coatings will be affected by multiple thermal shocks (Ref 11). Consequently, conception and validation of the flexural strength measurement after subjecting the coatings to a temperature difference appears highly relevant. Beyond describing the scatter and scale of the strength either prior or after thermal shock, both characteristics could be further utilised for the estimation of component lifetime under static or cyclic load, as described by Munz and Fett (Ref 5).

Experimental

All specimens were produced using commercial alumina rods (Rokide A) as feedstock and a MasterJet flame-spray gun (both from Saint-Gobain, Avignon, France). The molten alumina droplets were projected onto a graphite substrate (GM-154e, Graphite Materials, Oberasbach, Germany). Due to the differences in thermal expansion behaviour of graphite and alumina, the flame-sprayed alumina coatings detached after cooling down and could be removed from the graphite substrate without rupture. Table 1 lists the used settings for the thermal-spray process.

Table 1 Fuel and feed settings for the flame-spray process (Nm3—standard cubic metre)
Full size table

For ball-on-three-balls testing (B3B), discs of 0.5 mm in thickness and 8 mm in diameter were produced. This was realised by spraying onto the plane circular face of a graphite cylinder of the same diameter until the desired thickness was reached. Furthermore, thin stripes of two different sizes were prepared for four-point-bending tests (geometry I: 1.5 × 10 × 30 mm3 and geometry II: 1.5 × 10 × 45 mm3). Here, a side face of a graphite bar of either 10 × 30 mm2 or 10 × 45 mm2 was employed to set the basic specimen shape. The coating process was again terminated, as the intended coating thickness was attained. The spray distance between the torch and the graphite substrate amounted 100 mm in all spray trials. Both methods of preparation hold the advantage that none of the specimens required any further preparation prior to testing. It should be noted that thermal spraying was established as a coating technology, hence predominately aims for wide coatings of thicknesses less than 1 mm. The preparation of large free-standing components with dimensions  > 1 mm is strongly related to the process itself and requires a delicate control of the process conditions such as spray distance and angle. Otherwise, rupture appears as consequence of e.g. temperature gradients within the component during spraying. That would represent a pre-testing or pre-application selection, which is considered impermissible. To maintain the coating character of the tested specimens and to keep the moment of inertia feasible, the thicknesses of the free-standing coatings were kept below 1 mm. In order to assess the suitability of the three geometries for statistical strength characterisation, the proportion of rejects r (specimens, not possible to remove from the substrate without rupture) was considered before measuring the flexural strength. This ratio was calculated by r = 1 − k/ka, where k is the number of usable specimens and ka the number of spray attempts, here fixed at 15. A reject proportion of r = 1 would thus mean that 0 specimens out of 15 spray attempts could be used, while 15 specimens out of 15 spray attempts were usable when r = 0 applies. For r < 0.05, a geometry was considered suitable for the estimation of the Weibull parameters. Consequently, both stripe geometries needed to be excluded from strength testing, since none of them fulfilled this condition (rI = 0.13, rII = 0.40). In contrast, the reject proportion of the disc geometry was 0. This resulted in two test series for evaluating m and σ0, 0TS and 1TS with 43 specimens each, as listed in Table 2.

Table 2 Test series for ball-on-three-balls testing (TS—Number of thermal shocks)
Full size table

For thermal shock, the specimens were annealed at 1000 °C for 30 min before being subjected to sudden quenching in water of 20 °C (stationary). Hence, the resulting temperature gradient ΔT amounted 980 K. The change of water temperature was neglectable due the sheer differences between total mass of all specimens per run (30 g to 50 g) and the mass of the water (10 kg). Since a stationary water bath was used, the bath depth was set to 10 cm in order to allow the specimens to sink through the water in the first moments of quenching. This was meant to minimise the impacts of local thermal insulation due to bubble formation at the specimen surface, as the bubbles detached during the sinking movement. It can be noted that neither an increase in water temperature nor bubbles could be observed. The total time between leaving the furnace and reaching the bottom of the water bath amounted less than 2.5 s.

The internal structure of the material before and after thermal shock was characterised on disc specimens by the aid of 3D-image processing through x-ray microtomography. Such was realised in a CT-Alpha (Procon x-ray GmbH, Germany) equipped with a Dexela detector (1944 pixel × 1526 pixel, type 1512, Perkin Elmer Inc.). Voxels of 9.8 μm edge length after reconstruction were given, due to the sample dimensions and position in between x-ray gun and detector.

The flexural strength was calculated from the maximum load at rupture Fc, the specimen thickness t, and the dimensionless factor f*, depending on Poisson’s ratio ν as well as the ratio of specimen thickness or support radius Ra to the specimen radius R:

$$\sigma_{\text{c,B3B}} = {\text{f}}^{*} \left( {\frac{t}{R},\frac{{R_{\text{a}} }}{R},\nu } \right)\frac{{F_{\text{c}} }}{{t^{2} }}$$
(1)

The underlying thickness of the specimens was determined in the centre, near the region of the maximum flexural momentum. A further detailed description of the test method and an empirical formula for f* can be found in the literature (Ref 12). Some major advantages are the simple specimen geometry, the adaptivity for different specimen sizes, the tolerance against geometrical imperfections of the specimen, and a potential adaptation for elevated temperatures. In the present study, the Poisson’s ratio ν was approximated with 0.2, as done by Neumann et al. (Ref 8) for fracture mechanical considerations of free-standing flame-sprayed alumina. For the B3B test, the radius of the used ceramic balls (alumina) was 2.5 mm and the supporting radius Ra was calculated from that according to Börger et al. (Ref 12). Loading in B3B was performed with a loading rate of 0.05 mm min−1. In all bending tests, the specimen face, which represented the former contact face between substrate and coating, was subjected to tensile stresses. The strength data of both test series were statistically analysed in terms of Weibull theory according to EN 843-5 (2006), resulting in the (unbiased) Weibull modulus m (scatter parameter) and the characteristic strength σ0 (scale parameter). For the 0TS-series, the dependence of the strength on the specimen size was analysed following the Weibull theory, as described by Eq. 2. The derived characteristic strength of the B3B-tests was transformed according to the effective surface area for four-point-bending bars of 3 × 5×45 mm3 (as tested by Neumann et al. (Ref 8)) and for three-point-bending stripes of 0.8 × 10 × 40 mm3 (as tested by Aneziris et al. (Ref 7)). The mean effective surface area Seff of the B3B-discs was calculated using a FEM-model with specimen diameter and mean specimen thickness (Ref 13). Thus, the surface-related characteristic strength of both other bending tests σb is given by:

$$\sigma_{b} = \sigma_{0} \left( {\frac{{S_{eff} }}{{S_{b} }}} \right)^{1/m}$$
(2)

In here, σ0 is the characteristic strength of the corresponding test series. The effective surface area Sb of a 3 × 5 × 45 mm3 bar in four-point bending or a 0.8 × 10 × 40 mm3 stripe in three-point bending was calculated according to Quinn (Ref 14).

Results and Discussion

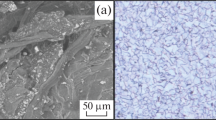
A first indicator for their thermal shock performance can be found as all specimens survived the quenching from 1000 °C without rupture and therefore could be tested for flexural strength. In Fig. 1, x-ray tomography scans of a disc prior (A) and post (B) thermal shock are displayed. Major cracks are indicated by arrows. From Fig. 1(a), one can see that in the as-sprayed state microcracks are visible, although difficult to visualise due to the given voxel size. Since SEM-micrographs of flame-sprayed alumina, presented in the literature, show a pronounced network of microcracks though, it is assumed that the majority of these cracks would appear smaller in extension than the resolution of the tomography scans would allow for visualisation (Ref 2). In turn, after thermal shock, next to these narrow cracks (black arrows) wider, more pronounced cracks are visible (white arrows), as shown in Fig. 1(b). Figure 1(c) showcases the lateral view of the thermal shocked specimen. In the emphasised region, it can be seen that the crack arrested within the volume. Hence, the propagation of the thermal shock-induced cracks (macrocracks) was restrained. As proposed by Aneziris et al. (Ref 7), such inhibition could be attributed to the present microcrack network. In agreement with that, pronounced R-curve behaviour could be evinced for flame-sprayed alumina, according to which the energy required for crack advance increases for a propagating crack. Reasons for the increase in crack resistance were outlined as energy consumptions due to the opening of the microcrack network and meandering of the macrocrack. In sum, such mechanisms result in a reduction in energy available for the growth of the macrocrack (Ref 8).

Fig. 1
figure 1

X-ray tomography scans of the central plain of thermally sprayed alumina prior (a) and post (b) one thermal shock (TS) from 1000 °C to room temperature (voxel-edge length = 9.8 μm). Subfigure (c) shows the lateral view of the thermal shocked specimen. Arrows indicate major cracks (black: pre-existing microcracks, white: thermal shock-induced macrocracks)

Full size image

Figure 2 shows exemplary load–displacement diagrams for B3B-testing before (black line) and after thermal shock (grey line). Similar for both is the nonlinear part near maximum loads. It is assumed that this deviation from linearity is related to subcritical crack growth of the present microcracks as a certain range of stress intensity is reached at their tips. Comparable behaviour can be seen from cyclic-loading tests of pre-notched specimens (Ref 8). The apparent linear part in the beginning of the loading, however, resembles four-point-bending results, published by Neumann et al. (Ref 8) for flame-sprayed alumina of higher thicknesses. Since this linear behaviour is visible here too, the concepts of linear elastic fracture mechanics could be considered valid for thin and for bulk alumina material, prepared by flame-spray technology (Ref 8).

Fig. 2
figure 2

Typical load versus displacement relation of the as-sprayed 0TS-series (black line) and the 1TS-series after one thermal shock (TS) from 1000 °C to room temperature (grey line). The specimen thickness was similar for both selected specimens

Full size image

Taking the thickness of the discs into account, this geometric characteristic appeared scattered around the aimed 0.5 mm as well due to the rather chaotic flame-spray process. In Fig. 3, the measured flexural strength is plotted against the individual specimen thickness. As one can see, there is no clear trend or relation between both, neither for series 0TS, nor for series 1TS. Eventually, this hints for only minor influence of specimen thickness within the given range. It should be noted that for the lowest investigated specimen thicknesses (0.3–0.4 mm) individual strength values before and after thermal shock evinced about a similar scale. Again in individual cases, a comparable situation was found for thicknesses between 0.7 and 0.8 mm. Within the central range of investigated specimen thickness (0.4–0.7 mm), the differences between flexural strength before and after thermal shock appeared more pronounced. To which extend such results could be attributed to a potential impact of thickness upon strength degradation through thermal shock or in turn to the natural scatter of the strength itself, remains an issue to be addressed in further specified investigations. For the present study though, Weibull analysis is performed covering all measurements per test series, also since the amount of data gets smaller for the aforementioned outer regions of specimen thicknesses. In that, the cumulative analysis allows for a general overview regarding sub-millimetre coatings and acts as starting point for future studies.

Fig. 3
figure 3

Flexural strength plotted against specimen thickness for the as-sprayed 0TS-series (black dots) and the 1TS-series after one thermal shock (TS) from 1000 °C to room temperature (open triangles)

Full size image

The resulting Weibull parameters of both test series are listed in Table 3, together with the upper and lower bound (90% confidence band). Comparing 0TS and 1TS, a drop in the characteristic strength of about 49% is visible, which meets the expectation for a thermal shock around 1000 K, derived from the studies of Aneziris et al. (Ref 7), as discussed above. Moreover, an obvious difference can be derived for the scatter of strength data. The Weibull modulus decreased by a factor of about 3 after thermal shocking. Compared to the Weibull modulus of hot-isostatic pressed alumina (m = 11.8), m of the flame-sprayed alumina is lower by a factor of approximately 2 in the as-sprayed state and by a factor of about 6 after one thermal shock 1TS (Ref 15). Thus, the scatter of the strength was already large for the as-sprayed state. As the scatter of the strength is caused by the scatter of the flaw size, the Weibull modulus m dropped further for the 1TS series. However, the modest strength drop as consequence of the sudden quench in water is considered remarkable, when compared to strength degradation reported for sintered polycrystalline alumina (Ref 10). The derived range of the Weibull modulus m also matches the results of Aneziris et al. (Ref 7) regarding the as-sprayed state (Weibull modulus of 4.7). Other reports, addressing the variation of strength data of thermally sprayed compounds, e.g. Ostojic and Berndt (Ref 16), consider the results of tensile adhesion tests (TAT). There, a Weibull modulus of 3.3 can be found for the bond strength of thin alumina coatings, which is also of the same scale as the obtained Weibull modulus from this study. The Weibull plots of the strength data are given in detail in Fig. 4. As one can see, there are no outliers since all strength values can be found within the 90% confidence bands.

Table 3 Weibull modulus m and characteristic strength σ0, determined from 43 specimens per test series (brackets contain 90% confidence band according to EN 843-5; TS—Number of thermal shocks)
Full size table
Fig. 4
figure 4

Weibull plot of the strength data for the as-sprayed 0TS-series (black dots) and the 1TS-series after one thermal shock (TS) from 1000 °C to room temperature (open triangles). Solid and dashed lines represent linear fits and 90% confidence bands, respectively

Full size image

Considering a theoretical strength range of 0 MPa to 140 MPa, the probability density of flexural strength is plotted in Fig. 5 applying either of both distributions. Parameters of the Weibull distribution are the determined Weibull modulus and characteristic strength of the corresponding test series (without confidence band). Parameters of the Normal distribution are the mean and standard deviation, calculated from the 43 strength values per test series. As one can see, the deviation between Weibull and Normal distribution is rather low for 0TS, while the contrast in estimation for 1TS is more distinct, especially since for a strength of 0 MPa a probability density > 0 is predicted. Hence, addressing a rough estimation and scatter of the flexural strength in the as-sprayed state, arithmetic mean and standard deviation appear adequate for thin flame-sprayed alumina coatings. Comparable results are assumed to apply for flame-sprayed materials with similar melting temperatures, as their microstructure would be similar. Addressing strength degradation and scatter after thermal shock, Weibull analysis could be preferred according those findings, as the arithmetic mean would underestimate the scale of strength degradation. Hence, the thermal shock performance could be overestimated.

Fig. 5
figure 5

Comparison of Weibull and Normal distribution of strength data prior (black) and after thermal shock (TS) from 1000 °C to room temperature (grey)

Full size image

The recalculation of the characteristic strength for four-point and three-point bending was performed using the determined characteristic strength σ0 for the as-sprayed state and its confidence band. Moreover, the determined Weibull modulus m and its upper and lower bounds were taken into account to calculate the effective surface area Sb. For the calculation of the mean effective surface area of the B3B-discs Seff only the median m was implemented. The results are listed in Table 4. Clearly, the decrease in strength for an increase in effective surface is visible. The prediction of three-point-bending strength by Weibull theory is in good agreement with the scale of flexural strength, reported by Aneziris et al. (Ref 7) for specimens without any further surface treatment like polishing or cutting (flexural strength of 28.8 MPa). Hence, for this comparison, the estimation of the size effect by Weibull theory is considered suitable. However, the resulting values for 3 × 5×45 mm3 bars do not match the scale of flexural strength, reported for as flame-sprayed alumina in bulk form (flexural strength of 105.7 MPa) (Ref 8). It should be mentioned that back then the investigated bulk specimens had cut, thus quasi-polished surfaces. This step of specimen machining is assumed to minimise the effects of surface flaws and their contribution to the fracture process, which shifts the measured strength towards higher values than predicted by Weibull theory.

Table 4 Transformed (surface-related) characteristic strength σb for three- (3PB) and four-point-bending (4PB) prior to thermal shock including confidence band of σ0;B3B and Weibull modulus m (further acronyms: B3B—ball-on-three-balls testing, l—lower, u-upper)
Full size table

To extrapolate the observed effects in the Weibull statistics to different thermal shock temperature gradients, further tests are required. According to Hasselman (Ref 9, 10), for polycrystalline alumina, the strength as function of the thermal history (ΔT) undergoes four different stages, determined by the two critical thermal shock gradients ΔTc and ΔT’c (0 < ΔT < ΔTc, ΔT = ΔTc, ΔTc < ΔT < ΔT’c, ΔT > ΔT’c). Only in the first stage (ΔT < ΔTc), no change of the strength can be expected. At ΔT = ΔTc, fracture is initiated and thus strength decreases discontinuously (Ref 9). Therefore, it can be assumed that the characteristic strength is depending on the thermal shock gradient, if ΔT > ΔTc. In flame-sprayed alumina, Aneziris et al. (Ref 7), evinced a two-stage behaviour of the strength as function of ΔT. Below ΔT = 800 K, the strength was approximately constant, before it degraded at higher ΔT. Thus, a significant change of the characteristic strength σc can be expected for thermal shock gradients above 800 K. However, a similar prediction for the Weibull modulus m as a function of ΔT cannot be given, and therefore, the statistical measure m has to be determined discretely in dependence on the thermal shock conditions and thus on the microstructural evolution.

Conclusion

Scope of the presented research was the statistical treatment of flexural strength data of thin flame-sprayed alumina coatings (free-standing) prior and after thermal shock by standard Weibull method. The obtained results allowed for the following conclusions:

  • From the experimental aspects, the B3B-method allowed for the investigation of the flexural strength of thin flame-sprayed alumina coatings at room temperature without any pre-test selection. In perspective, the B3B-method also appears suitable for flexural testing at elevated temperatures.

  • As expected, the scatter of flexural strength is higher for flame-sprayed alumina coatings when compared to the Weibull modulus e.g. reported for hot-isostatic pressed alumina.

  • Thermal shock decreases the characteristic strength of flame-sprayed alumina according to the prediction and increases the scatter of flexural strength.

  • For a rough estimation of median strength and strength scatter in the as-sprayed state, arithmetic mean and standard deviation based on a normal distribution appear adequate. This however can not be applied for the flexural strength after thermal shock.

Further potential studies could address the impact of repetitive thermal shocks.