Abstract
Suspension high velocity oxy-fuel thermal spray typically utilizes axial injections of suspension into the combustion chamber. There are certain cases where the oxygen-sensitive nanoparticles benefit from a reduction in the time and temperature spent in the gas flow. Therefore, a radial injection outside of the nozzle can enable deposition of oxygen-sensitive nanomaterials. This study investigated the effect of the suspension flow rate, angle of injection and the injector diameter on the in-flight particle conditions. The combustion reaction is modeled using the eddy dissipation concept model with a robust reaction mechanism and compared to the current approach within the literature. This approach has not been employed within SHVOF thermal spray and provides a robust treatment of the reaction mechanisms. The suspension was modeled using a two-way coupled discrete particle model. Experimental observations were obtained using high-speed imaging, and observations of the liquid jet were compared to the numerical values.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
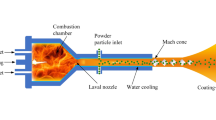
Surface engineering is a field of study that looks to alter the properties of substrate surface to increase its lifespan and durability and to reduce the surface degradation. One common approach in surface engineering is coating the surface of a substrate with a protective layer. Hence, the field of thermal spray arose to allow for the deposition of materials onto the surface of substrates to produce a protective coating. High velocity oxy-fuel (HVOF) thermal spray was developed in the 1980s to allow for the deposition of dense coatings to coat surfaces of a substrate in a protective coating. Suspension HVOF is a subset of HVOF thermal spray that allows for the deposition of nanoparticles using a suspension feedstock. Typically, in SHVOF thermal spray, premixed fuel and oxygen are injected into a combustion chamber where the mixture undergoes combustion. The suspension is then injected axially into the combustion chamber where it undergoes primary breakup, secondary breakup and evaporation. The nanoparticles are then deposited onto the surface of a substrate. There is a significant body of the modeling literature investigating the effect of different parameters for axial injections of suspension within the combustion chamber for SHVOF thermal spray. Tabbara et al. (Ref 1) looked at axially injecting water droplets into the combustion chamber, to investigate the effect the initial droplet diameter has on the evaporation rate. Other studies by Mahrukh et al. (Ref 2,3,4) looked at the effect of different axial injection types, models for suspension properties and the effect of an atomization model on the droplet breakup and evaporation rates. Taleby et al. (Ref 5) investigated the effect of gas flow rate, suspension flow rate, droplet diameter and the droplet velocity for an axial injection of ethanol droplets. Emami et al. (Ref 6) looked at comparing the eddy dissipation model (EDM) with the eddy dissipation concept model (EDC) within a warm spray system. Warm spray is conceptually very similar to SHVOF thermal spray with the main distinguishing feature consists of an inert gas injection within the combustion chamber to control the combustion chamber temperature. This study found a significant change in the temperature profile with the EDC model within the free jet region.
There are certain cases where the quality of the coating as well as the efficiency of deposition or the functionality of the coating can be significantly enhanced through a radial injection of suspension outside of the nozzle. Oxygen-sensitive materials such as graphene, carbon nanotubes and fullerene oxidize and degrade readily when heated and exposed to oxygen for significant durations of time. Therefore, a radial injection of suspension can reduce in-flight time and may allow for their deposition. There is an abundance of research that has been focused on modeling SHVOF thermal spray with an axial injection. To the best of the authors’ knowledge, there are no numerical studies on modeling SHVOF thermal spray with a radial injection of suspension outside of the gun. There have been a few experimental studies conducted that have utilized a radial injection of suspension into a HVOF jet (Ref 7).
There are several numerical studies within suspension plasma spray (SPS) injecting suspension radially into the plasma jet. Amirsaman et al. (Ref 8) looked at the effect of different viscosity models for the suspension. Jabbari et al. (Ref 9) looked at the effect of the suspension velocity, location and the angle of injection within suspension plasma spray. Jadidi et al. (Ref 10) looked the effect of different substrate shapes on SPS thermal spray. Cécile et al. (Ref 11) looked at the effect of a plasma jet on droplet breakup for a radially injected droplet. Meillot et al. (Ref 12) looked at modeling the interaction of a liquid jet and a plasma torch using a VOF model.
Traditionally, in SHVOF thermal spray, there has been little success in deposition using a radial injection of suspension, as opposed to SPS where this injection method has been more successful. The reason for this is in plasma spray gas temperatures can reach values of up to 14,000 K as opposed to SHVOF thermal spray where temperatures are of the order of 2200-3000 K. Hence, the gas densities are much lower than that for SHVOF thermal spray. This allows for the suspension jet to penetrate deeper within the plasma jet. The major hurdle in radial injection for SHVOF thermal spray is to provide the liquid jet with sufficient momentum to penetrate into the center of the gas jet while ensuring that there is not an excessive loss in heat and momentum. This study aims to develop a numerical model for a radial injection in SHVOF thermal spray. The effect of suspension flow rate, injection angle and the diameter of the injector on the in-flight particle conditions were investigated. For the numerical model, the commercial CFD software ANSYS Fluent V19.0 (Ref 13, 14) (Pennsylvania, USA) was employed. For the experimental investigation, a high-speed camera was employed to allow for the imaging of the liquid jet to validate the numerical results.
Numerical Modeling
A fully structured 3-D mesh of 2.25 million cells was employed to model the fluid domain. The premixed fuel and air were injected into the combustion chamber using an annular inlet located 4 mm from the center of the combustion chamber and with a width of 1 mm. A steady-state gas flow field was established before injecting any suspension. To model the gas phase, the continuity, momentum conservation, ideal gas law, energy conservation, species fraction and the realizable k-ε turbulence model with a standard wall function are solved for using the SIMPLE algorithm and the QUICK scheme for the convective terms (Ref 3). The details of the governing equations have been omitted and can be found in our prior study (Ref 15). The discrete phase is injected using a two-way coupled discrete particle model (DPM) (Ref 16). The cone injection type consists of 20 particle streams has been employed for the suspension injection. A cone angle of 1° has been calculated based upon the research of Ranz (Ref 17). A two-way turbulence coupling, secondary breakup model and the pressure-dependent boiling options have been employed within the discrete phases submodels. The unsteady discrete phase is solved for once with every ten gas-phase iterations with a DPM time step of 1 × 10−5 s. The inverse distance node-based averaging of the source term is employed to distribute the DPM source term among neighboring cells (Ref 18). The boundary conditions for the gas phase and the discrete phase are outlined in Table 1 (Fig. 1).
Prior SHVOF thermal spray studies (Ref 19,20,21) have looked to model the combustion using the species transport model with a single-step mechanism and the eddy dissipation model (EDM) (Ref 4). However, this modeling approach simplifies the chemistry into a global reaction and does not include some intermediate species that form such as HO2 and H2O2. There is no account for any measurement of the turbulence within the combustion chamber while determining the equilibrium composition. This approach also requires rate-determining coefficients for the eddy dissipation model that must be calibrated to match experimental values. Due to the inability to measure the reaction rate within the combustion chamber, the default values must be used. This in turn has an adverse effect on the gas temperature profile and species composition profile (Ref 15). The EDC model has been recently implemented within warm spray (Ref 6) and found to provide a significant improvement in modeling the combustion outside of the nozzle. Hence, this study has employed the EDC model along with a detailed reaction to model the combustion, which is given in Table 2 along with the chemical kinetics.
Here, to model the combustion reaction, a global combustion mechanism has been obtained for hydrogen combustion (Ref 22). The mechanism is reduced using the directed relation graph (DRG) method in ANSYS Chemkin for the operating conditions within the combustion chamber (Ref 23). The error in removing a species and a mechanism is calculated using Eq 1. If the error is below the user-specified error, the species can be removed. Further information on the mechanism reduction method can be found in (Ref 24, 25)
The eddy dissipation concept (EDC) is an extension to the EDM model to account for detailed reaction mechanisms in turbulent combustion flows (Ref 26), and the symbols are outlined within the nomenclature. The EDC model assumes the reaction occurs in a thin region typically smaller than the computational grid. The model distinguishes the cell into two subzones; the reacting fine structures and the surrounding fluid. The reaction is confined to the fine-scale structures, and the fine-scale structures are treated as being adiabatic, isobaric, plug flow reactors (PFR). Turbulent mixing transfers mass and energy from the fine structures to the surrounding fluid. The length scale of the fine structures is given by Eq 2; the volume fraction of the fine scale is given by the cube of this length scale. Species are assumed to react over the time scale given in Eq 3. Assuming the reaction occurs only within the fine structures, the net reaction rate is determined by Eq 4 (Ref 27)
Suspension Modeling
The suspension is modeled using a two-way coupled DPM model with a multicomponent droplet injection. A multicomponent injection is a droplet comprised of multiple species. The properties of the droplet such as the specific heat and density are calculated from the volume average of the various constituent components. The viscosity is calculated using the correlation proposed by Guth et al. (Ref 8) to include the effect of the nanoparticles on the viscosity of the droplet. The surface tension is given by the surface tension of water below the boiling point of water, and above the melting temperature of Al2O3 the surface tension for molten alumina is employed. The thermal physical properties of water and Al2O3 are given in Tables 3 and 4, respectively. The motion of the droplets is given by Newton’s second law, with the significant force operating on the particles being the drag force. The drag coefficient, CD, is given by the correlation by Crowe (Ref 28) which considers the effect of the Mach number and the Reynolds number on the drag coefficient (Ref 29). The particle temperature can be determined from a heat balance on the suspension droplet, assuming no internal temperature gradient within the droplet. The heat transfer coefficient is computed using the Ranz and Marshall (Ref 14) correlation. The droplet specific heat and density are modified according to a weighted volume average of the solid and liquid components. To model the evaporation, the convection/diffusion-controlled evaporation model has been employed (Ref 4), with pressure-dependent boiling and turbulence coupling. Further information can be found in our prior study (Ref 15).
To model the liquid jet, the “blob” method has been employed (Ref 30) which is one of the most popular approaches found in the literature due to its simplicity. The jet injection is reduced to an injection of “blobs” with an equivalent diameter of the injector. The blobs are subject to secondary breakup from the crossflow and evaporation. At large Weber numbers, the droplet breakup can be characterized by the KHRT breakup model (Ref 1). The KHRT breakup model assumes the breakup time and droplet sizes are related to the fastest growing Kelvin–Helmholtz instabilities on the droplet surface within the liquid core. Outside of the liquid core, it is assumed that breakup is driven by the aerodynamic forces with the Rayleigh–Taylor instabilities. The Suspension flow rate, angle of injection and the diameter of injector are varied and a summary of the injection parameters is given in Table 5.
Experimental Methodology
High-speed imaging can be used to image the injection of suspension to provide a comparison against experimental observations. High-speed imaging has been used in a wide range of applications to allow for a comparison of numerical models with experimental observations. For example, radial injection of suspension is very common in suspension plasma spray (SPS); therefore, shadowgraphy is often used in SPS to validate the numerical models (Ref 9, 31).
The Phantom V12 (Ametek, Pennsylvania, USA) high-speed CCD camera with the sigma 70-300 mm F4-5.6 lens was used to capture images of the suspension injection. The camera was placed in view of the suspension injection 0.45 m in front of the spray gun, and the lighting system is used to provide back illumination. A panel of glass was placed in front of the camera to protect the camera. A white background was placed 0.3 m behind the thermal spray system to allow for a contrast between the liquid jet and the background as shown in Fig. 2. A flame of 75 kW was obtained as this flame power allowed for a supersonic flame which is the characteristic feature of SHVOF thermal spray (Ref 32). A higher flame power was avoided as very high gas velocities would prevent any suspension from penetrating the gas jet at all. A liquid jet of suspension composing of suspension 14 weight percent Al2O3 and water was then injected radially into the flame at a distance of 10 mm downstream from the nozzle exit and 22 mm above the centerline. The alumina suspension used has a D50 ~ 137 nm, D10 ~ 83 nm and a D90 of ~ 225 nm (Ref 33). The mass flow rate was monitored via a flow rate meter to ensure the desired flow rate. A background image was taken without any injection of suspension to allow the removal of the background from the images. Once the liquid injection matched the desired flow rate, a series of pictures were then taken at a frame rate of ~ 5 × 102 per second and the images were processed using ImageJ (NIH, Maryland, USA). The raw images are converted to a binary image by applying a threshold within ImageJ (NIH, USA), and a threshold value of 22% was applied to the images (Ref 31).
Results and Discussion
Validation
The location of breakup and the windward trajectory of the suspension into the flame is examined as illustrated in Fig. 3. Figure 4(a), (b), (c), (d), (e) and (f) shows still images for a radial injection as the flow rate of the liquid jet is varied from 50, 100, 150, 200, 250 and 300 mL/min, respectively.
Image of radial injection of an Al2O3 and water suspension into a 75 kW flame with varying liquid injection flow rates, with an injection location of 10 mm downstream from the nozzle outlet and 22 mm above the jet axis centerline. (a) 50 mL/min, (b) 100 mL/min, (c) 150 mL/min, (d) 200 mL/min, (e) 250 mL/min and (f) 300 mL/min
To validate the model, numerical values of the location of the breakup of the jet from the centerline and the jet trajectory of the jet are compared with experimental values. Figure 5 compares the experimentally obtained values of the location of the breakup of the suspension jet, respectively, to the numerical values at varying flow rates. Figure 5 shows good agreement between the numerical model and the experimentally observed value of the location of the breakup. As the suspension flow rate increases, the discrepancy between experimental values and numerical values becomes smaller. At a flow rate of 50 mL/min, there is a discrepancy of 1 mm and at 300 mL/min, there is a discrepancy of 0.2 mm between the numerical and experimental value. Figure 6(a) plots the jet trajectories at suspension flow rates of 50-300 mL/min; it can be seen as suspension flow rate increases, the jet penetrates further into the HVOF flame. Figure 6(b) compares the jet trajectories from the numerical results against that of experimental values at 150 and 250 mL/min. It can be seen that there is a high degree of consistency between the numerical and experimentally obtained value of the jet trajectory in the region beyond the column.
In summary, the employed “blob” method to model the suspension injection with a multicomponent droplet and the KHRT secondary breakup model provides good agreement with experimental measurements for the distance of penetration and the breakup location. The distance of breakup shows improved consistency at higher flow rates. The distance of penetration shows a high degree of coherence at the entire range of flow rates investigated.
Comparison of Combustion Model
In SHVOF and HVOF thermal spray, the eddy dissipation model (EDM) model with a global reaction mechanism is the most commonly used approach to model the combustion. This model overpredicts the gas temperature in comparison with the adiabatic flame temperature as reported within our prior study (Ref 15). It is also commonly reported that the EDM model underpredicts the particle temperatures by up to 500 K within the free jet in contrast to experimental measurements (Ref 6). A recent study compared the EDC model with the EDM model for a warm spray application (Ref 6) and found higher gas temperatures within the free jet using the EDC model and hence mitigates some error associated with the underprediction in the particle temperatures within the free jet.
Figure 7 compares the centerline static gas temperature using the EDC model and the EDM model. The global reaction mechanism employed for the EDM model is given by Eq 5, and the reaction is rounded to 4 decimal places. From Fig. 7, it can be seen that a combustion chamber temperature of 3200 K is calculated from the EDC model, and this matches the adiabatic flame temperature 3200 K. The adiabatic flame temperature is calculated from software Gordan and McBride (NASA CEA) (Ref 34) at the combustion chamber pressure of 2.6 bar and an equivalence ratio of 1. The EDM model severely overpredicts the adiabatic flame temperature within the combustion chamber by over 350 K. It can also be seen that there is a significant difference between the slopes of the temperature curves in the free jet. This is a result of ambient oxygen mixing and further reacting with the gas jet, and the detailed reaction mechanism can resolve these reactions in greater detail than the global reaction mechanism which is solely determined to approximate the reaction within the combustion chamber as reported within (Ref 6). The overprediction in the gas temperature affects many aspects of the flow such as the gas density, the gas velocity, evaporation rates of suspension, particle temperature and the particle velocities. The EDC provides a significant improvement in the calculation of the gas temperature within the combustion chamber as opposed to the EDM model currently employed in the literature. Figure 8(a) and (b) shows a center plane contours of gas velocity field and temperature field, respectively, without any suspension injection. From Fig. 8, it can be seen that the shocks are resolved, and there are five shock diamonds presented in Fig. 8(a). Typically, in SHVOF 6-7 shocks are witnessed within outside of the gun (Ref 35), which compares well with the value reported in literature.
Numerical Investigation into the Effect of Suspension Flow Rate
Figure 9 shows a center plane contour of the gas velocity with varying suspension volume flow rate from 50 to 300 mL/min. Figure 10 shows the centerline gas velocity magnitude as the suspension flow rate is varied. It can be seen that as the suspension flow rates increases up to 100 mL/min, the centerline gas velocity is near identical to the gas velocity without any suspension injection. With further increases in the suspension flow rate above 100 mL/min, the centerline velocity of the gas jet reduces significantly.
Figure 11 shows a center plane contour of the temperature with the suspension flow rate varying from 50 to 300 mL/min. Figure 12 shows the centerline static gas temperature as the suspension flow rate is varied from 50 to 300 mL/min. Figure 11 shows that low suspension flow rates have little effect on the static gas temperature. As the suspension flow rate increases the temperature decreases significantly. As the suspension flow rate increases from 50 mL/min to 300 mL/min the temperature along the centreline decreases by an additional 1800 K, as measured from 20 mm from the nozzle exit.
Figure 13 shows a center plane contour of the Mach number at varying suspension flow rates from 50 to 300 mL/min. From Fig. 13, it can be seen that a bow shock forms in the location of the penetration of the suspension jet within the supersonic region of the flow. At low suspension flow rates, the effect of the suspension injection is small due to the low penetration of the suspension jet into the suspension crossflow. As the suspension flow rate increases, the suspension is able to penetrate deeper into the crossflow. The bow shock trails the suspension injection in the windward direction.
Figure 14 shows the injection of suspension into the flame and the particle locations within the gas jet for varying suspension flow rate of 50, 100, 150, 200, 250 and 300 mL/min. Figure 14 illustrates how the suspension injection is modeled within the study and how the suspension is injected into the gas jet. It can be seen that as the suspension flow rate increases, the droplets penetrate further into the gas stream. It is reported in the literature that for a liquid jet in a crossflow, penetration of the liquid jet into the gas jet requires the dynamic pressure of the liquid jet to exceed that of the gas jet as indicated by Eq 6 (Ref 36). This equation shows us that with a higher velocity (flow rate), the suspension can penetrate further into the gas jet due to the higher dynamic pressure of the liquid jet.
Figure 15 shows the suspension particle velocities at a downstream distance of 85 mm from the nozzle exit for a varying suspension flow rate of 50-300 mL/min. The particle velocity scatter plots are capped at 800 m/s for all results as very few particles reach this velocity and only for certain suspension injection conditions. The in-flight particle conditions were evaluated 85 mm as this is the typical standoff distance for axially injected suspension. Nanoparticles have low mass and thermal inertia due to their size. The gas velocity and temperature drop off significantly beyond 85 mm; hence, particles decelerate and cool rapidly beyond this region.
It can be seen that, as the suspension flow rate is increased to 200 mL/min, there is an increase in the maximum particle velocity. As the suspension flow rate is increased from 50 to 200 mL/min, the maximum particle velocity increases from 450 to 950 m/s. As the suspension flow rate is increased further from 200 to 300 mL/min, the maximum velocity of the particles then begins to decrease from 950 to 500 m/s. As the suspension flow rate increases from 50 to 200 mL/min, the higher penetration of the suspension results in a higher maximum particle velocity. As the suspension flow rate increases further, the significant reduction in the gas velocity results in the lower maximum particle velocity. As the suspension flow rate increases there is a greater momentum transfer from the gas to the suspension, which results in lower gas velocities. Hence, the optimum flow rate to maximize particle velocities at the standoff distance of 85 mm from the gas nozzle exit lies within the region of 150-200 mL/min.
Figure 16 shows the average in-flight particle velocity for the suspension flow rates investigated. It can be seen that as the suspension flow rate increases, the average velocity of the particles increases up to 50 mm downstream from the nozzle exit. As the particles decelerate, the rate of deceleration is dependent on the mass of the particles. At lower suspension flow rates, the particles decelerate at a lower rate due to the higher moisture content. Therefore, further downstream this trend is broken due to the greater deceleration of particles that are injected at a higher suspension flow rate. The average particle velocity at 50 mL/min shows an anomalous trend in comparison with the remaining flow rates. This is a result of a lower droplet radial velocity and a low penetration of the droplets which results in heavy particles with high moisture content. These heavy particles are less susceptible to turbulent fluctuations; hence, these particles do not stray out of the gas jet to any great degree. The particles continue to accelerate, while at higher suspension flow rates particles decelerate as they travel out of the gas jet. Downstream from the nozzle exit, with the suspension flow rate at 50 mL/min, particles are able to maintain their momentum significantly better than that for higher flow rates. This would imply that the particles at 50 mL/min are significantly heavier and therefore very little if at all any liquid is vaporized at this flow rate.
Figure 17 shows the suspension particle temperatures at standoff distance of 85 mm for a varying suspension flow rate of 50 to 300 mL/min. It can be seen that as the suspension flow rate is increased from 50 to 300 mL/min, a greater proportion of particles are heated. It can also be seen that as the suspension flow rate increases from 50 to 150 mL/min, the maximum particle temperature increases from 400 to 2000 K. As the suspension flow rate increases above 150 mL/min, the maximum temperature the particles reach reduces significantly. As the suspension flow rate increases from 150 to 300 mL/min, the maximum particle temperature decreases from 2000 to 1450 K. With the increase in the suspension flow rate, particles are able to penetrate deeper into the gas jet. This allows for greater heat transfer to the in-flight particles, and hence, the maximum particle temperature increases as the suspension flow rate increase to 150 mL/min. However, as the suspension flow rate increases further the addition of more suspension into the gas removes greater quantities of heat from the gas jet which results in the lower temperatures of the gas jet and hence lower maximum particle temperatures. The melting temperature of Al2O3 is 2072 K (Ref 37); therefore, excessively high suspension flow rates prevent particles from being heated sufficiently to become near molten.
Figure 18 shows the average in-flight particle temperature at a varying suspension flow rates of 50 to 300 mL/min. In general, it can be seen that increasing the suspension flow rate from 50 to 300 mL/min results in a higher average particle temperature further downstream from the nozzle exit around the region of 150 mm. An increase in the suspension flow rate from 50 mL/min to 300 mL/min results in an increase in the average particle temperature of approximately 140 K at a location of 150 mm from the nozzle exit. As the suspension flow rate increases the average particle temperature increases as more particles are heated.
It can be seen that as the suspension flow rate increases, the particles become more scattered. This is a result of greater evaporation of suspension at higher flow rates; particles are significantly lighter for higher flow rates. Lighter particles move out of the gas jet easily due to the turbulent nature of the flow. As the particles move out of the jet, they cool and decelerate rapidly due to their low thermal and mass inertia. Ensuring these particles do not stray out of the flow can significantly improve inlight particle characteristics.
A major challenge in radial injection SHOVF thermal spray is ensuing that the suspension can sufficiently penetrate the gas jet. It is concluded that a high injection velocity is required to allow for a high penetration of suspension into the gas jet. A high penetration of the suspension is required to maximize heat and momentum transfer to the particles. The injection velocity can be increased by increasing the suspension flow rate. This, however, results in greater removal of heat and momentum from the flame and hence reduces the maximum velocity and temperature the particles are able to obtain. Operating at a low suspension flow rates does not significantly impact the gas velocity or the gas temperature. However, the low suspension penetration at low flow rates results in low particle velocities and temperatures. As the flow rate increases, the jet penetration increases which allows for more particles to be heated and accelerated as the proportion of particles that reach the center of the gas jet increases. Further increase in the suspension flow rate results in a significant removal of heat and momentum from the flames. This results in a significant reduction in the maximum temperature and velocity that the particles can obtain. An optimum suspension flow rate to maximize particle temperatures lies within the range of 100-150 mL/min as this suspension flow rate leads to particles that are molten upon impact and looks to maximize the proportion of particles that are heated. The optimum suspension flow rate to maximize particle velocities lies within the range of 150-200 mL/min.
Numerical Investigation into the Effect of Angle of Injection
Using a 100 mL/min injection flow rate, the suspension injection angle has been varied. Three injection angles are considered: an angle of positive 15°, 0° and negative 15°. A positive injection angle occurs with the suspension injection angled in the direction of the gas flow. A negative injection angle is defined as the liquid jet traveling in the direction opposing the gas flow. Figure 19 shows the average velocity of particles at various standoff distances for the three injection angles investigated. Figure 19 shows that, as the angle of injection varies from the positive value of 15° to the negative value of 15°, the velocity of the particles decreases. With a positive injection angle, particles are given an initial velocity in the direction of the flow. Hence, a positive injection angle results in a higher in-flight particle velocity due to the higher initial X velocity in the flow direction.
Figure 20 shows the average in-flight temperature of particles for the three injection angles investigated. Figure 20 shows that as the angle of injection varies from the negative value of 15° to the positive value of 15°, the average temperature of the particles decreases. With a negative injection angle, particles must be decelerated and then be accelerated in the direction of the flow. This allows for the particles to spend a greater duration of time within the flame and hence allow for greater heating of the particles.
In summary, varying the angle of injection can significantly influence the in-flight particle conditions. The particle thermal properties should be considered when deciding on the angle of injection. With a positive angle of injection, suspension droplets are given a larger initial velocity in the direction of the gas flow; hence, particles have a higher in-flight velocity. With a negative injection angle, the suspension droplets initial velocity opposes the gas jet. The suspension droplets must first be decelerated and then accelerated in the direction of the gas flow. Droplets and particles spend a greater duration of time within the flame, and therefore, higher particle temperatures are seen for a negative injection angle. The injection angle can be adjusted to match additional heat requirements for particles with a high melting temperature. Or the injection angle can be modified to match the additional momentum requirements of in-flight particles of low melting temperatures. With Al2O3-based suspension, the high melting point of the particles and low sensitivity to oxygen at high temperatures makes a negative injection angle beneficial. This results in greater heating of particles to increase the quantity of molten in-flight particles.
Numerical Investigation into the Effect of Diameter of Injection
In this investigation, three injection nozzle diameters were considered; the flow rate of 100 mL/min and an angle of negative 15° has been used. The injector diameter was varied at 0.3, 0.45 and 0.6 mm. Figure 21 shows the particle velocity at a standoff distance of 85 mm from the nozzle exit for varying injector diameters of 0.3, 0.45 and 0.6 mm. Figure 21 shows that as that as the diameter of the injector decreases, the velocity of the particles increases. It is also seen that as the injector diameter decreases, the maximum velocity the particles can increases. With the injector diameter of 0.3 mm particles reach a maximum velocity of 900 m/s, as the injector diameter increases to 0.6 mm the maximum particle velocity reduces to 500 m/s. Figure 22 shows the average in-flight particle velocities for the varying injector diameters of 0.3, 0.45 and 0.6 mm. From Fig. 22, it can be seen that decreasing the injector diameter from 0.6 to 0.3 mm the maximum average particle velocity increases from 240 to 440 m/s.
Figure 23 shows the particle temperature at a standoff distance of 85 mm from the nozzle exit for varying injector diameters of 0.3, 0.45 and 0.6 mm. Figure 23 shows that as the diameter of the injector reduces, there is a greater proportion of particles that are heated. Figure 24 shows the average in-flight particle temperatures for the varying injector diameters of 0.3, 0.45 and 0.6 mm. It is seen that as the injector diameter decreases, the maximum temperature the particles can reach increases. With the injector diameter of 0.3 mm, a greater proportion of the particles are heated to a near molten state. As the higher velocity allows greater penetration of suspension into the gas jet therefore, particles are exposed to higher gas temperatures which result in the higher particle temperatures.
From Fig. 21 and 23, it can be seen that at lower injector diameters particles stray out of the jet more readily. With a higher velocity injection, the larger radial component of the velocity as well as the lighter particle mass due to greater liquid evaporation is resulting in particles exiting the gas jet. As the particles exit, the jet the particles quickly lose their heat and momentum due to their low mass and thermal inertia. Ensuring particles remain within the gas jet is a challenge that will need to be addressed when injecting suspension radially for SHVOF thermal spray. Further analysis on ensuing that particles do not stray out of the gas jet would significantly improve coating depositions within radially SHVOF thermal spray.
It has been shown that increasing the suspension flow rate results in greater penetration of the suspension into the gas jet due to the higher injection velocity. The injection velocity can also be increased by reducing the injector diameter at a fixed flow rate. With a smaller suspension injector diameter, the higher injection velocity of the suspension increases the penetration of the suspension into the gas jet, which significantly increases the proportion of particles heated without capping the maximum velocity and temperature the particles can obtain. Reducing the diameter of the injector comes with its own limitations as the injector is more prone to clogging as the diameter shrinks. Therefore, when using a radial injection of suspension, one must optimize both the suspension flow rate along with the injector diameter to minimize clogging of the injector and to maximize the in-flight particle velocities and temperatures.
Conclusions
This study employs the use of detailed reaction mechanisms along with the EDC combustion model and investigates the effect of the combustion model on the adiabatic flame temperature within the combustion chamber. This model avoids the overprediction in the flame temperature as seen in prior SHVOF thermal spray studies. This approach provides a more rigorous treatment of the combustion of unburnt fuel with ambient oxygen that mixes into the jet. The injection of suspension within the model is validated against experimentally obtained observations using high-speed imaging of the suspension injection. The DPM model with a multicomponent injection provides a robust treatment of the liquid jet.
This paper demonstrates the importance of carefully optimizing the suspension injection parameters, as well as the consideration that is required for the suspension injector for radial injection of suspension in SHVOF thermal spray. The injection conditions must ensure sufficient momentum to penetrate into the gas jet but not as to adversely cool or decelerate the jet. Injectors that maximize the injection velocity can allow for the use of lower suspension flow rates and hence increase in-flight particle velocities and temperatures. Angling the injection with a consideration of the material properties in mind can allow for one to decide if the in-flight particles will benefit from an injection angle that favors high velocity or an angle of injection that favors high temperatures. From this study, it is clear that the injection parameters and the injector geometry can drastically improve the in-flight particle behavior. This study has demonstrated the feasibility in utilizing a radial injection of suspension as well as the importance to properly calibrate the suspension injection conditions, providing an optimistic outlook for the deposition of oxygen-sensitive materials using a radial injection of suspension.
Abbreviations
- C τ :
-
Time scale constant = 0.4082
- C ξ :
-
Volume fraction constant = 2.1377
- r AB :
-
Error introduced from the removal of species B onto Species A
- V A,i :
-
Stoichiometric coefficient of species A in the ith reaction
- ω i :
-
Reaction rate of the ith reaction
- Y * i :
-
Fine-scale mass fraction
- τ*:
-
Reaction time scale
- Y :
-
Vapour mass fraction
- We :
-
Weber number
- δ Bi :
-
Delta function, value 1 if reaction contains species B
- ξ*:
-
Length fraction of fine scales
- d:
-
Particle diameter
- g:
-
Gas
- l:
-
Liquid
- p:
-
Particle
- s:
-
Value at droplet surface
- Al2O3 :
-
Aluminium oxide
References
H. Tabbara and S. Gu, A Study of Liquid Droplet Disintegration for the Development of Nanostructured Coatings, AIChE J., 2012, 58(11), p 3533-3544
M. Mahrukh, A. Kumar, and S. Gu, Effects of Angular Injection, and Effervescent Atomization on High-Velocity Suspension Flame Spray Process, Surf. Coat. Technol., 2016, 302, p 368-382
M. Mahrukh, A. Kumar, S. Gu, S. Kamnis, and E. Gozali, Modeling the Effects of Concentration of Solid Nanoparticles in Liquid Feedstock Injection on High-Velocity Suspension Flame Spray Process, Ind. Eng. Chem. Res., 2016, 55(9), p 2556-2573
E. Gozali, M. Mahrukh, S. Gu, and S. Kamnis, Numerical Analysis of Multicomponent Suspension Droplets in High-Velocity Flame Spray Process, J. Therm. Spray Technol., 2014, 23, p 940-949
M. Taleby and S. Hossainpour, Numerical Investigation of High Velocity Suspension Flame Spraying, J. Therm. Spray Technol., 2012, 21, p 1163-1172
S. Emami, H. Jafari, and Y. Mahmoudi, Effects of Combustion Model and Chemical Kinetics in Numerical Modeling of Hydrogen-Fueled Dual-Stage HVOF System, J. Therm. Spray Technol., 2019, 1(1), p 1-13
F.-L. Toma, L.M. Berger, D. Jacquet, D. Wicky, I. Villaluenga, Y.R. De Miguel, and J.S. Lindeløv, Comparative Study on the Photocatalytic Behaviour of Titanium Oxide Thermal Sprayed Coatings from Powders and Suspensions, Surf. Coat. Technol., 2008, 203, p 2150-2156
A. Farrokhpanah, T. Coyle, and J. Mostaghimi, Numerical Study of Suspension Plasma Spraying, J. Therm. Spray Technol., 2016, 26(1–2), p 12-36
F. Jabbari, M. Jadidi, R. Wuthrich, and A. Dolatabadi, A Numerical Study of Suspension Injection in Plasma-Spraying Process, J. Therm. Spray Technol., 2014, 23(1–2), p 3-13
M. Jadidi, M. Mousavi, S. Moghtadernejad, and A. Dolatabadi, A Three-Dimensional Analysis of the Suspension Plasma Spray Impinging on a Flat Substrate, J. Therm. Spray Technol., 2014, 24(1–2), p 11-23
C. Marchand, A. Vardelle, G. Mariaux, and P. Lefort, Modelling of the Plasma Spray Process with Liquid Feedstock Injection, Surf. Coat. Technol., 2008, 202(18), p 4458-4464
E. Meillot, R. Vert, C. Caruyer, D. Damiani, and M. Vardelle, Manufacturing Nanostructured YSZ Coatings by Suspension Plasma Spraying (SPS): Effect of Injection Parameters, J. Phys. D Appl. Phys., 2011, 44(19), p 1-8
A. Fluent, ANSYS Fluent 12.0 User’s Guide, Vol 15317, Ansys Inc, Canonsburg, 2009, p 1-2498
I. Ansys, ANSYS FLUENT Theory Guide, Knowl. Creat. Diffus. Util., 2009, 15317(November), p 724-746
S. Chadha, R. Jefferson-Loveday, and T. Hussain, Effect of Nozzle Geometry on the Gas Dynamics and Evaporation Rates of Suspension High Velocity Oxy Fuel (SHVOF) Thermal Spray: A Numerical Investigation, Surf. Coat. Technol., 2019, 371, p 78–79.
E. Dongmo, A. Killinger, M. Wenzelburger, and R. Gadow, Numerical Approach and Optimization of the Combustion and Gas Dynamics in High Velocity Suspension Flame Spraying (HVSFS), Surf. Coat. Technol., 2009, 203(15), p 2139-2145
W.E. Ranz, Some Experiments on Orifice Sprays, Can. J. Chem. Eng., 1958, 36(4), p 175-181
S.V. Apte, K. Mahesh, and T. Lundgren, Accounting for Finite-Size Effects in Simulations of Disperse Particle-Laden Flows, Int. J. Multiph. Flows, 2008, 34(3), p 260-271
M. Mahrukh, A. Kumar, S. Gu, and S. Kamnis, Computational Development of a Novel Aerosol Synthesis Technique for Production of Dense and Nanostructured Zirconia Coating, Ind. Eng. Chem. Res., 2016, 55(28), p 7679-7695
E. Gozali, S. Kamnis, and S. Gu, Numerical Investigation of Combustion and Liquid Feedstock in High Velocity Suspension Flame Spraying Process, Surf. Coat. Technol., 2013, 228, p 176-186
J. Pan, S. Hu, L. Yang, K. Ding, and B. Ma, Numerical Analysis of Flame and Particle Behavior in an HVOF Thermal Spray Process, JMADE, 2016, 96, p 370-376
N.M. Marinov, A Detailed Chemical Kinetic Model for High Temperature Ethanol Oxidation, Int. J. Chem. Kinet., 1999, 3(31), p 183-220
Ansys, ANSYS Chemkin-Pro Reaction Workbench Manual ANSYS Chemkin-Pro ® Software, 2017.
T. Lu and C.K. Law, On the Applicability of Directed Relation Graphs to the Reduction of Reaction Mechanisms, Combust. Flame, 2006, 146(3), p 472-483
T. Lu and C.K. Law, A Directed Relation Graph Method for Mechanism Reduction, Proc. Combust. Inst., 2005, 30(1), p 1333-1341
B. Magnussen, On the Structure of Turbulence and a Generalized Eddy Dissipation Concept for Chemical Reaction in Turbulent Flow, in 19th Aerospace Sciences Meeting (American Institute of Aeronautics and Astronautics, Reston, Virigina, 1981), p 1-8.
A. De, E. Oldenhof, P. Sathiah, D. Roekaerts, A. De, E. Oldenhof, D. Roekaerts, and P. Sathiah, Numerical Simulation of Delft-Jet-in-Hot-Coflow (DJHC) Flames Using the Eddy Dissipation Concept Model for Turbulence-Chemistry Interaction, Flow Turbul. Combust, 2011, 87, p 537-567
C.T. Crowe, Drag Coefficient of Particles in a Rocket Nozzle, AIAA J., 1967, 5(5), p 1021-1022
M. Jadidi, S. Moghtadernejad, and A. Dolatabadi, Numerical Modeling of Suspension HVOF Spray, J. Therm. Spray Technol., 2016, 25(3), p 451-464
R.D. Reitz, Modeling Atomization Processes in High-Pressure Vaporizing Sprays, At. Spray Technol., 1987, 3(4), p 309-337
M. Jadidi, S. Moghtadernejad, and A. Dolatabadi, Penetration and Breakup of Liquid Jet in Transverse Free Air Jet with Application in Suspension-Solution Thermal Sprays, Mater. Des., 2016, 110, p 425-435
M. Bai, R. Khammas, L. Guan, J.W. Murray, and T. Hussain, Suspension High Velocity Oxy-Fuel Spraying of a Rutile TiO2 Feedstock: Microstructure, Phase Evolution and Photocatalytic Behaviour, Ceram. Int., 2017, 43(17), p 15288-15295
T.A. Owoseni, J.W. Murray, Z. Pala, E.H. Lester, D.M. Grant, and T. Hussain, Suspension High Velocity Oxy-Fuel (SHVOF) Spray of Delta-Theta Alumina Suspension: Phase Transformation and Tribology, Surf. Coat. Technol., 2019, 371, p 97–106.
I. Analysis, S. Gordon, A. Cleveland, and B.J. Mcbride, NASA Reference Computer Program for Calculation Complex Chemical Equilibrium Compositions and Applications, 1994.
M. Jadidi, S. Moghtadernejad, and A. Dolatabadi, A Comprehensive Review on Fluid Dynamics and Transport of Suspension/Liquid Droplets and Particles in High-Velocity Oxygen-Fuel (HVOF) Thermal Spray, Coatings, 2015, 5(4), p 576-645
L. Pawlowski, Suspension and Solution Thermal Spray Coatings, Surf. Coat. Technol., 2009, 203(19), p 2807-2829
R.H. Perry and D.W. Green, Perry’s Chemical Engineers’ Handbook, McGraw-Hill, New York, 2008
Acknowledgment
This work was supported by the Engineering and Physical Sciences Research Council [EP/N50970X/1]. Access to high-performance computing resources provided by the University of Nottingham and HPC midlands plus is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chadha, S., Jefferson-Loveday, R., Venturi, F. et al. A Computational and Experimental Investigation into Radial Injection for Suspension High Velocity Oxy-Fuel (SHVOF) Thermal Spray. J Therm Spray Tech 28, 1126–1145 (2019). https://doi.org/10.1007/s11666-019-00888-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11666-019-00888-8