1 Introduction

Short-fiber reinforced thermoplastics are increasingly used in load-bearing applications due to their process ability in molten state, high specific stiffness and strength. The high strength- and stiffness-to-weight ratio is of particular interest to the automotive industry due to the commitment of reducing the fuel consumption and lowering the CO2 emission by weight reduction (Ref 1, 2). Structural parts are typically produced using injection-molding, enabling complex geometries at high volume rates. During injection molding, the flow conditions vary throughout the product resulting in a process-induced fiber orientation (Ref 3,4,5) with associated directionality of the mechanical properties.

Describing the deformation behavior and predicting the ultimate failure of short-fiber reinforced thermoplastics is of upmost importance to utilize them in application-critical structural parts. This is however challenging considering the heterogeneity of the stress state, directionality of the mechanical properties, the intrinsic time-dependent behavior of the matrix material and that failure originates locally depending on the local stress state caused by the fiber arrangement as demonstrated via scanning electron microscopy (Ref 6,7,8) and micro-CT imaging (Ref 8,9,10,11,12,13,14). Moreover, a direct consequence of the presence of the reinforcing constituent is the development of thermal residual stresses in the material. These stresses arise due to the mismatch in coefficient of thermal expansions between fiber and matrix material, high processing temperatures and inhomogeneous cooling. The thermal residual stresses have a considerable impact on the local stress state (Ref 15, 16) and on the warpage of injection-molded products affecting dimensional stability (Ref 17, 18).

The magnitude of the thermal residual stress scales with the modulus, temperature difference, mismatching coefficient of thermal expansion (CTE) and processing conditions. For example, a higher cooling rate results in an increase in residual stress due to the viscoelastic nature of the thermoplastic material. The residual stress starts to build up once the polymer is cooled below the glass-transition temperature. Above this temperature relaxation takes place almost immediately due to the high segmental mobility of the polymer chains. The coefficient of thermal expansion of the matrix material is an order of magnitude higher resulting in a considerable larger volumetric shrinkage compared to the fiber. Due to shrinkage, the overall stress state is compressive in the fiber, while the stress in the matrix is tensile along the fiber flank and compressive around the fiber ends. This distribution of residual stress can affect the deformation behavior and the failure initiation which is already abundantly studied for continuous-fiber reinforced composites (Ref 19,20,21,22,23,24,25). In contrast, its short-fiber reinforced counterpart has not received much attention (Ref 15, 16, 26). Pan et al. (Ref 15) studied the effect of thermal residual stress on the interfacial debonding of a single-fiber micromechanical model with a realistic description of the matrix phase where it was shown that debonding occurs at an higher applied strain when the thermal residual stress is accounted for. Chen et al. (Ref 16) used a two-fiber micromechanical model to study effect of fiber arrangement on the thermal residual stress using elastic material properties. The magnitude of thermal residual stress increases with decreasing inter-fiber distance, and it increases with increasing orientation angle between the two fibers. Wu et al. (Ref 26) performed a statistical analysis on simulations of a realistic microscopic model under thermal and mechanical loading using an elastic material model. They concluded that the local von Mises stresses show a small offset toward higher values when the thermal residual stress are accounted for.

Measuring thermal residual stress in short-fiber reinforced materials is experimentally challenging (Ref 27). Several techniques are applied to measure the thermal residual stress in composites. Examples are photo-elasticity (Ref 28, 29) and Raman spectroscopy on aramid fibers or carbon materials (Ref 25, 30,31,32,33). These techniques require great experimental effort and dedicated equipment. In this study, we have chosen to investigate the thermal residual stress within short-fiber reinforced thermoplastics numerically. For this study, realistic 3D representative volume elements (RVE) of the microstructure are used. The RVE gives a realistic prediction of the deformation on a nominal stress and strain level while at the same time provide information on the local heterogeneous stress fields (Ref 34,35,36,37,38). In this study, the RVE is used to determine the effect of the thermal residual stress on the evolving heterogeneous stress state within a multi-fiber environment and on the nominal mechanical properties, i.e., Young’s modulus and yield stress for a range of fiber-weight fractions. Based on the insights generated by our micromechanical models we shed light on the necessity to include thermal residual stresses for a proper failure analysis of short-fiber reinforced thermoplastics. Modeling of the thermal residual stress is realized by implementing thermal strains in a viscoelastic viscoplastic material model for glassy polymers, the Eindhoven glassy polymer (EGP) model. The build-up of thermal residual stress for unreinforced polycarbonate (PC) is measured experimentally using a DMTA setup by cooling a thin strip from above the glass-transition temperature to room temperature. The implementation of the thermal residual stress within the EGP model opens the door to systematically study the effect of thermal residual stress on the local and nominal stress state of the short-fiber reinforced thermoplastics. The study is organized as follows: Firstly, the experimental study on the thermal residual stress is outlined. Following, the numerical procedure on the micromechanical model is presented. Finally, the description of the thermal residual stress and the results of the simulations are discussed and concluded.

2 Experimental

2.1 Materials and Sample Preparation

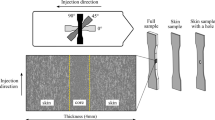
The material used is a commercial grade of polycarbonate (Lexan 141R), which is kindly provided by Sabic innovative plastics (Bergen op Zoom). Small rectangular plates are compression molded in a mold with a thickness of 0.2 mm. A small thickness is used to minimize the thermal gradient and to accommodate for the limited force range of the DMTA. Prior to processing, the material was dried in a vacuum oven at 120 °C for 12 h. The plates are held at the processing temperature of 250 °C for 3 min at 50 kN. Afterward, the material is cooled down to room temperature. Rectangular bars are punched from of the plates.

2.2 Mechanical Testing

The procedure for measuring the thermal residual stress is schematically shown in Fig. 1. The thermal residual stress is measured with a rectangular geometry setup in tensile mode on a DMA 850 dynamic mechanical analyzer from TA Instruments as shown in Fig. 2. The sample is heated to a temperature of 145 °C which is above the glass-transition temperature of polycarbonate. As a reference, the glass-transition temperature at 1 °C s−1 measured by DSC is equal to 143.5 °C [39]. When the furnace reaches the required temperature a dwell time of 5-10 min is obeyed to reach a stable temperature. With the sample equilibrated, its length is fixed and measured to set the thermally expanded length to the zero point. Afterward, the temperature is reduced with a constant cooling rate of 3 °C·min−1, while the sample is constrained and the residual thermal stress can be measured.

Fig. 1
figure 1

Procedure for measuring the thermal residual stress build-up during cooling: unconstrained heating (1), stress-free relaxation (2) and constrained cooling (3)

Full size image
Fig. 2
figure 2

Thermal residual stress build-up during cooling measured in a DMTA

Full size image

2.3 Experimental Results

The measured thermal residual stress is shown in Fig. 2. Initially, the thermal residual stress builds up gradually starting from a temperature of 140 °C; the temperature of 140 °C is used as the glass-transition temperature for this cooling rate and experimental method, and becomes linear well below the glass-transition temperature. Close to the glass-transition temperature, structural relaxation is fast due to the high segmental mobility of the polymer chains. Therefore, the thermal residual stresses that arise are relaxed equally fast. Well below the glass-transition temperature, stresses start to develop within the timescale of the experiment due to the decrease of the segmental mobility of the polymer chains with temperature. Note that the glass-transition temperature is not a fixed material parameter and depends strongly on the measurement method to capture the range in which the material transitions from rubber to glassy behavior (Ref 39). The determined glass-transition temperature depends on the timescale of the experiment, i.e., cooling rate. The effect of cooling rate on the build-up of thermal residual stress is not measured in our study due to the limited force range and cooling rate of the DMTA.

3 Numerical Methods

The representative volume elements (RVEs) consist out of two phases: a matrix and a fiber phase, see Fig. 3. The mechanical deformation behavior of the fiber is modeled by a linear elastic material model with a Young’s modulus of 72 GPa, a Poisson’s ratio of 0.22 and a coefficient of thermal expansion of 5 × 10−6 K−1. The matrix phase is modeled using the Eindhoven glassy polymer (EGP) model with a coefficient of thermal expansion whose value is discussed in the next section. The EGP model is able to capture the intrinsic response of the glassy polymer, including the nonlinear viscoelastic behavior, plastic flow and post-yield behavior. The intrinsic deformation, i.e., true stress versus true strain, of polycarbonate as can be measured in uniaxial compression (Ref 40) or video-controlled uniaxial tensile tests (Ref 41) is shown in Fig. 4. Initially, the material shows a viscoelastic response up to the yield point. After yield, the material shows strain softening which is a decrease in stress with deformation followed by strain hardening which is an increase in stress upon deformation. This intrinsic deformation of PC is modeled by the multi-mode EGP model which consists of multiple parallel connected Maxwell elements. The mechanical analog of the multi-mode EGP model is shown in Figure 5. All simulations are performed using MSC. Marc (Ref 42) where the constitutive model is implemented in the user subroutine HYPELA2.

Fig. 3
figure 3

The micromechanical model for the multi-fiber representative volume element (RVE) for a fiber weight fraction of 30%. The fibers are colored gray. The main fiber direction is in the z direction

Full size image
Fig. 4
figure 4

True stress–strain response in uniaxial compression denoting the regions of the intrinsic deformation behavior of polycarbonate

Full size image
Fig. 5
figure 5

Mechanical analog for the multimode EGP model

Full size image

3.1 Constitutive Model

The thermal deformation gradient tensor in the EGP model is defined as:

$$\begin{array}{*{20}c} {{\varvec{F}}_{{{\text{th}}}} = \exp \left( {\alpha \left( {T - T_{0} } \right)} \right){\varvec{I}},} \\ \end{array}$$
(1)

where \(\alpha\), \(T\), \(T_{0}\) and \({\varvec{I}}\) are the coefficient of thermal expansion, current temperature, initial temperature and the second-order unit tensor, respectively. The mechanical deformation gradient is determined by dividing the total deformation tensor by the thermal deformation gradient tensor:

$$\begin{array}{*{20}c} {{\varvec{F}}_{m} = {\varvec{F}}_{{{\text{tot}}}} \cdot {\varvec{F}}_{{{\text{th}}}}^{ - 1} .} \\ \end{array}$$
(2)

The mechanical deformation gradient tensor is multiplicative decomposed into a plastic and elastic part:

$$\begin{array}{*{20}c} {{\varvec{F}}_{m} = {\varvec{F}}_{e} \cdot {\varvec{F}}_{p} ,} \\ \end{array}$$
(3)

where the subscripts e and p denote the elastic and plastic part. The total stress is divided into a hardening \({\varvec{\sigma}}_{r}\) and a driving term \({\varvec{\sigma}}_{s}\) following the example of Haward and Thackray [43]:

$$\begin{array}{*{20}c} {\sigma = {\varvec{\sigma}}_{{\text{s}}} + {\varvec{\sigma}}_{{\text{r}}} . } \\ \end{array}$$
(4)

The hardening term is described using a neo-Hookean relation as follows:

$$\begin{array}{*{20}c} {{\varvec{\sigma}}_{r} = G_{r} \overline{\varvec{B}}^{d} , } \\ \end{array}$$
(5)

where \(G_{r}\) and \(\overline{\varvec{B}}^{d}\) are the hardening modulus and the deviatoric part of the isochoric left Cauchy–Green deformation tensor. The driving stress is further divided into a hydrostatic and deviatoric \({\varvec{\sigma}}_{s}^{d}\) part:

$$\begin{array}{*{20}c} {{\varvec{\sigma}}_{s} = {\varvec{\sigma}}_{s}^{h} + {\varvec{\sigma}}_{s}^{d} . } \\ \end{array}$$
(6)

The hydrostatic stress equals:

$$\begin{array}{*{20}c} {{\varvec{\sigma}}_{s}^{h} = \kappa \left( {J - 1} \right){\varvec{I}},} \\ \end{array}$$
(7)

where \(\kappa\) and J are the bulk modulus and volume ratio. The volume ratio J is defined as the determinant of the elastic deformation gradient tensor which equals the determinant of the mechanical deformation gradient tensor as a results of the volume invariant plastic deformation.

$$\begin{array}{*{20}c} {J = \det \left( {{\varvec{F}}_{e} } \right) = \det \left( {{\varvec{F}}_{m} } \right).} \\ \end{array}$$
(8)

The driving stress is modeled using a combination of n parallel linked Maxwell elements:

$$\begin{array}{*{20}c} {{\varvec{\sigma}}_{s}^{d} = \mathop \sum \limits_{i = 1}^{n} {\varvec{\sigma}}_{s,i}^{d} = \mathop \sum \limits_{i = 1}^{n} G_{i} \overline{\varvec{B}}_{e,i}^{d} , } \\ \end{array}$$
(9)

where \(G\) and \(\overline{\varvec{B}}_{e}^{d}\) denote the shear modulus and the deviatoric part of the isochoric, elastic left Cauchy-Green deformation tensor. The subscript \(i\) refers to a specific Maxwell element. The plastic rate of deformation is related to the deviatoric component of the driving stress using a non-Newtonian flow rule with modified Eyring equations:

$$\begin{array}{*{20}c} {{\varvec{D}}_{p,i} = \frac{{{\varvec{\sigma}}_{s,i}^{d} }}{{2\eta_{i} }},} \\ \end{array}$$
(10)

where \(\eta_{i}\) is the viscosity defined by an Eyring flow rule:

$$\begin{array}{*{20}c} {\eta_{i} = \eta_{{0,i,{\text{ref}}}} \left( T \right)\frac{{\overline{\tau }/\tau_{0} }}{{\sinh \left( {\overline{\tau }/\tau_{0} } \right)}}\exp \left( {\frac{\mu p}{{\tau_{0} }}} \right)\exp \left( S \right),} \\ \end{array}$$
(11)

where \(\eta_{{0,i,{\text{ref}}}}\) is the initial viscosity for the reference state at a given temperature, \(\mu\) is the pressure dependency parameter which describes the effect of pressure on yield, and \(\tau_{0}\) is the characteristic shear stress which describes the deformation kinetics. The equivalent stress \(\overline{\tau }\) and pressure \(p\) are defined as follows:

$$\begin{array}{*{20}c} {\overline{\tau } = \sqrt {\frac{1}{2}{\varvec{\sigma}}_{s}^{d} :{\varvec{\sigma}}_{s}^{d} } , } \\ \end{array}$$
(12)
$$\begin{array}{*{20}c} {p = - \frac{1}{3}{\text{tr}}\left( {{\varvec{\upsigma}}} \right).} \\ \end{array}$$
(13)

The influence of temperature on the viscosities is described as follows:

$$\begin{array}{*{20}c} {\eta_{{0,i,{\text{ref}}}} \left( T \right) = \eta_{{0,i,{\text{ref}}}}^{*} \left( T \right)\exp \left( {\frac{\Delta U}{{RT}}} \right).} \\ \end{array}$$
(14)

Here \(\eta_{{0,i,{\text{ref}}}}^{*} \left( T \right)\) is the absolute, temperature independent, initial viscosity, \({\Delta }U\) the activation energy, \(R\) the gas constant and \(T\) the absolute temperature. Strain softening is modeled using the parameter \(S\) in the viscosity:

$$\begin{array}{*{20}c} {S = S_{{\text{a}}} \cdot R\left( {\overline{{\gamma_{p} }} } \right).} \\ \end{array}$$
(15)

Its initial value equals the state parameter \(S_{a}\) and reduces to zero under plastic deformation by mechanical rejuvenation described using a modified Carreau–Yasuda relation \(R\left( {\overline{{\gamma_{p} }} } \right)\) (the value for \(R\left( {\overline{{\gamma_{{\text{p}}} }} } \right)\) goes from 1 to 0 with increasing equivalent plastic shear strain \(\left( {\overline{{\gamma_{p} }} } \right)\). The material model parameters to describe polycarbonate using the EGP model are summarized in Tables 1 and 2 and are taken from Van Breemen et al. (Ref 44). For more information on the EGP model, constitutive equations and its characterization, the reader is referred to Ref 44,45,46,47.

Table 1 Reference spectrum for polycarbonate at room temperature (T = 22 °C). Taken from [44]
Full size table
Table 2 Material parameters used in the EGP model to describe polycarbonate at room temperature (T = 22 °C). Taken from [44]
Full size table

3.2 Geometry

The geometries are generated using Digimat-FE (Ref 48) and consist of fibers that are placed within the simulation volume to match a given fiber orientation tensor. The fiber orientation tensor is a symmetric second-order tensor to mathematically describe the fiber orientation and its distribution. The tensor is computed by determining the dyadic product of the individual fiber orientation and averaging within a volume:

$$\begin{array}{*{20}c} {P = \oint {{\varvec{pp}}{\text{d}}p = \left\langle {pp} \right\rangle .} } \\ \end{array}$$
(16)

The fiber orientation tensor used in this study is equal to the fiber orientation tensor typically measured experimentally in the shear layer of the material (Ref 4):

$$\begin{array}{*{20}c} {P = \left[ {\begin{array}{*{20}c} {0.24} & {0.01} & {0.01} \\ {0.01} & {0.01} & { - 0.07} \\ {0.01} & { - 0.07} & {0.75} \\ \end{array} } \right].} \\ \end{array}$$
(17)

The fibers have an aspect ratio of 20 and are rounded with a radius of 15% of their diameter. A cylinder with straight ends may be more close to reality, but the straight ends will result in convergence issues. The fiber diameter is equal to 0.15 and the size of the RVE is 2 × 1 × 4 which is the same for all RVEs. The number of fibers in the RVE is equal to 15, 24 and 32 for a fiber-weight fraction of 20, 30 and 40% which is equivalent to a fiber volume fraction of 10.5, 16.7 and 23.8 %. The fibers are placed at a minimum allowed distance of 25% of its diameter to ensure that the fibers are not in contact with each other and to minimize extreme localization of deformation. The generated geometry is periodic, meaning that if a fiber crosses a face of the RVE, the part which falls outside the RVE will enter from the opposing face. The resulting finite element mesh must be periodic as well which is realized by meshing the three principal faces and consequently copying it to the opposing face creating a periodic mesh. The element type used is a quadratic tetrahedral element. The meshing is performed using Hypermesh (Ref 49). Due to the presence of the more rigid fibers, a gradient in deformation is anticipated around the fibers. Therefore, the element size for the fiber phase is 4 times smaller as the matrix phase resulting in an enforced gradient in element size. An element size of 1/5 of the fiber diameter is used for the fiber phase.

3.3 Boundary Conditions

A schematic representation of the loadcases used in the simulations is shown in Fig. 6. During the cooling phase, the temperature is homogeneously lowered from above the glass-transition temperature to room temperature at a constant cooling rate of 3 °C min−1. Afterward, stress relaxation occurs at room temperature for a period of 106 seconds. Finally, a nominal deformation is applied at a constant true strain rate of 10−3 s−1. Periodic boundary conditions are applied on the RVE to enforce continuity in displacement between the opposing planes. The local deformation of one plane \(\Gamma_{ijkl}\) is linked to the other plane plus the prescribed displacement \(\vec{u}_{i} - \vec{u}_{1}\):

$$\vec{u}_{{\Gamma_{6237} }} = \vec{u}_{{\Gamma_{5148} }} + \vec{u}_{2} - \vec{u}_{1} ,$$
$$\vec{u}_{{\Gamma_{8437} }} = \vec{u}_{{\Gamma_{5126} }} + \vec{u}_{4} - \vec{u}_{1} $$
(18)
$$\vec{u}_{{\Gamma_{5678} }} = \vec{u}_{{\Gamma_{1234} }} + \vec{u}_{5} - \vec{u}_{1} ,$$

where subscript \(i\) refers to the corner node \(i\), \(\vec{u}\) denotes the position vector of the nodes, and \(\Gamma_{ijkl}\) is the face through the corner nodes as indicated in Fig. 7. A displacement is applied parallel (z direction) or perpendicular (x direction) to the main fiber direction, while no deformation is applied in the other directions making them stress-free. Simulations are stopped at 4% nominal strain, which is well above the strains where these systems experimentally fail. The RVE is fixed on the corner nodes preventing rigid body motions and rotations as indicated in Fig. 7.

Fig. 6
figure 6

Schematic representation of the loadcases for the simulations. Cooling, relaxation and loading phase

Full size image
Fig. 7
figure 7

Boundary conditions applied on the representative volume element (RVE). The larger arrows in the z direction and x direction correspond to the loading condition applied parallel and perpendicular to the main fiber direction, respectively

Full size image

The results of the RVE are analyzed using the volume-averaged stress representing the nominal response. The local, heterogeneous stresses are analyzed using the local elemental stresses as determined in our RVE simulations. The volume averaged stress tensor is determined as follows:

$$\begin{array}{*{20}c} {{\varvec{\sigma}}_{M} = \frac{1}{V}\mathop \smallint \limits_{V} {\varvec{\sigma}}_{m} {\text{d}}V,} \\ \end{array}$$
(19)

where \(V\) and \({\text{d}}V\) denote the RVE volume and elemental volume. The subscripts M and m refer to the volume averaged values and the elemental values. The results of the simulations are discussed using scalar quantities for the deviatoric term, the von Mises stress \(\overline{\sigma }\), and for the volumetric term, the hydrostatic stress \(\sigma_{{\text{h}}}\). These scalar quantities are commonly used in describing the failure behavior of polymers [50,51,52,53,54,55]. The hydrostatic stress and von Mises stress are determined as follows:

$$\begin{array}{*{20}c} {\sigma_{{\text{h}}} = \frac{1}{3}{\text{tr}}\left( {\varvec{\sigma}} \right),} \\ \end{array}$$
(20)
$$\begin{array}{*{20}c} {\overline{\sigma } = \sqrt {\frac{3}{2}{\varvec{\sigma}}^{d} :{\varvec{\sigma}}^{d} } . } \\ \end{array}$$
(21)

4 Results and Discussion

4.1 Thermal Residual Stress

Before moving toward the result of the micromechanical model, the description of the build-up of thermal residual stress and the motivation behind its modeling strategy in the EGP model is discussed. Figure 8 shows the description (dashed line) of the thermal residual stress from the glass-transition temperature toward room temperature with a constant coefficient of thermal expansion of 50 × 10−6 K−1 which is found by fitting the slope to the experimental results. The glass-transition temperature of 140 °C is used as the stress-free temperature. The spectrum of moduli and viscosities used to describe the stress–strain behavior of polycarbonate, shown in Table 1, is used here as well. Clearly, this approach overestimates the thermal residual stress and is not an accurate method to describe the thermal residual stress. A more accurate description of the thermal residual stress can be reached by pragmatically offsetting the value for the glass-transition temperature and define what we here call the effective glass-transition temperature \(T_{{\text{g}}}^{\star}\) to match the experimental results. The description using this engineering approach with an effective glass-transition temperature is shown in Fig. 8 by the solid line and captures the data well. Of course we do realize that close to \(T_{{\text{g}}}\) equilibrium kinetics will influence the behavior (Ref 56). However our results using an effective glass-transition temperature show that it is not needed to include them for a good description well below \(T_{{\text{g}}}\).

Fig. 8
figure 8

Thermal residual stress build-up during cooling measured in the DMTA (symbols) and description by the numerical model using the glass-transition temperature \(T_{\text{g}}\) = 140 °C (dashed line) and the effective glass-transition temperature \(T_{\text{g}}^{\star}\) = 123 °C (solid line) as the stress-free temperature

Full size image

4.2 RVE Results

The simulations are performed in the three loading phases as schematically shown in Fig. 6. In the first phase, the temperature is homogeneously lowered from the effective glass-transition temperature down to room temperature. After the cooling phase, the residual stress is allowed to relax at room temperature for 106 seconds. Figure 9 shows the distribution of the local stress state for the matrix phase after the cooling and relaxation phase for RVEs with three different weight fraction of fibers via histograms that show the percentage of elemental volume which is at a certain stress value. The local stresses are discussed by the hydrostatic and von Mises stress which are scalar measures for the volumetric and deviatoric part of the stress tensor. Higher percentages indicate that more elemental volume is at the specific stress level. An increase in the fiber-weight fraction results in a broader distribution of local stresses and in an increase in local thermal residual stress. Note that the hydrostatic stresses are more sensitive to the increase in fiber-weight fraction due to the local volumetric confinement. The stress after the relaxation phase results in a small shift toward lower stress values. The stress levels are not high enough to cause a considerable lowering in stress due to relaxation.

Fig. 9
figure 9

Distribution of the local hydrostatic stress (a) and von Mises stress (b) after the cooling (solid) and relaxation phase (dotted) for a RVE containing 20%, 30% and 40% fiber-weight fraction

Full size image

After the relaxation phase, a deformation is applied parallel or perpendicular to the main fiber direction. Figure 10 shows the nominal stress strain curves parallel ∥ (left) and perpendicular ⊥ (right) to the main fiber direction. The solid lines show the stress strain curves for the simulation without the thermal residual stress, hence only the loading phase, while the dashed lines show the results with the thermal residual stress included. Obviously, increasing the fiber-weight fraction results in an increase in stiffness and strength. For both loading directions, no considerable difference in nominal stress is noted when the residual stress is accounted for.

Fig. 10
figure 10

Nominal uniaxial stress strain curve loaded parallel ∥ (a) and perpendicular ⊥ (b) to the main fiber direction for a RVE containing 20%, 30% and 40% fiber-weight fraction. The solid lines are the results without and the dashed with thermal residual stresses

Full size image

The distribution of the hydrostatic (left) and von Mises stress (right) for a deformation applied parallel (top) and perpendicular (bottom) to the main fiber direction at a nominal strain of 3.5% are shown in Fig. 11 for all three fiber-weight fractions. The solid lines are again the distribution for the simulation without the thermal residual stresses (only the loading phase) and the dashed lines the results with the thermal residual stresses. Accounting for the residual stress does not result in a different shape of the distribution. However, the magnitude in local stress differs. The hydrostatic stress is shifted toward higher values when the residual stress is accounted for while the von Mises stress stays approximately the same for both loading directions. The shift in hydrostatic stress is caused by the volumetric confinement of the matrix. Important to note is that the local hydrostatic stress is positive for a deformation applied perpendicular to the main fiber direction, whereas for a deformation applied parallel to the main fiber direction we also see regions experiencing compression. This connects well to the typically more brittle failure mode seen experimentally in the perpendicular direction.

Fig. 11
figure 11

The distribution of the hydrostatic (left) and von Mises stress (right) loaded parallel ∥ (top) and perpendicular ⊥ (bottom) to the main fiber direction for a RVE containing 20%, 30% and 40% fiber-weight fraction at a nominal strain of 3.5 %. The solid lines are the results without and the dashed with thermal residual stresses

Full size image

The difference in hydrostatic stress (left) and von Mises stress (right) between the simulations with and without the thermal residual stress is shown in Fig. 12 for the deformation applied parallel (top) and perpendicular (bottom) to the main fiber direction at a nominal strain of 3.5%. The shift in local hydrostatic stress depends on the fiber-weight fraction, higher weight fraction results in a larger shift in hydrostatic stress. The larger shift is a result of the increase in matrix volumetric confinement. The local stress upon deformation is similar for simulations including the thermal residual stress, but it is for the most part ahead in its local stress strain behavior in comparison with the case without thermal residual stress. The difference in local stress decreases upon deformation where the effect of thermal residual stress is leveled out earlier for the von Mises stress in comparison with the hydrostatic stress. In other words, the difference in local stress shown in Fig. 12 moves toward zero upon higher deformation and the difference in local von Mises stress for the bulk is zero at smaller deformation compared to the local hydrostatic stress. Most of the material is well into the strain hardening regime (see Fig. 4) where the difference between local von Mises stress with and without the thermal residual stress becomes negligible. In this region the molecular mobility is high, enabling fast relaxation of the thermal residual stresses.

Fig. 12
figure 12

The distribution of the difference in hydrostatic (left) and von Mises stress (right) between the simulation with and without thermal residual stress. The deformation is applied parallel ∥ (top) and perpendicular ⊥ (bottom) to the main fiber direction for a RVE containing 20%, 30% and 40% fiber-weight fraction at a nominal strain of 3.5%

Full size image

The hydrostatic stress does not necessarily follow trend as the von Mises stress and the difference in local stress between a simulation with and without the thermal residual stress is leveled out later. An additional numerical study has been conducted on an isolated single-fiber micro-mechanical model; the results have been added to Supplementary Information (SI). They present a detailed illustration of the effect of thermal residual stress on the evolution of the local stress state around a single fiber during loading. It is observed that the thermal residual stresses lead to an offset in strain in the build-up of the local von Mises stress, whereas the maxima remain unchanged.

5 Conclusion

We numerically studied the effect of thermal residual stress on the local and nominal stress state in a short-fiber reinforced thermoplastic. The finite element simulations show that to give an accurate quantitative description of the local stress state in a multi-fiber environment upon deformation one needs to take into account the thermal residual stresses. The qualitative distribution of the local stress, however, does not change. Studies focusing on the quantitative description of local failure mechanisms such as matrix cavitation or debonding of the fiber should therefore include the thermal residual stresses. On the other hand, the thermal residual stresses do not affect the nominal deformation behavior and global quantities such as the Young’s modulus of the short-fiber reinforced thermoplastics. Our study demonstrates that inclusion of thermal residual stress analysis is vital in assessing the correct local stress state in short-fiber reinforced thermoplastics, but is not required with respect to the macroscopic stress–strain response. The magnitude of local thermal residual stress is influenced by the modulus, coefficient of thermal expansion, as well as by crystallization-induced shrinkage (in case of semi-crystalline polymers). As a result, the quantitative local thermal residual stresses may vary for different systems, but it is anticipated that our observation that the macroscopic stress–strain response is not affected will also hold for other fiber-reinforced polymer systems. The reason is being that the evolution of local plasticity induces molecular mobility which enables fast relaxation of the thermal residual stress.

To calibrate the numerical model, we measured the thermal residual stress for a glassy polymer using a DMTA setup. This is achieved by heating the material close to the glass-transition temperature \(T_{{\text{g}}}\), applying the appropriate constraints followed by cooling at a constant cooling rate at which the thermal residual stress is measured. The thermal residual stress can be effectively modeled within a nonlinear viscoelastic–viscoplastic model, namely the Eindhoven glassy polymer (EGP) model, by an effective glass-transition temperature and a constant coefficient of thermal expansion. Capturing the complex equilibrium kinetics around the glass transition is not required to describe the thermal residual stress far below the glass-transition temperature.