1 Introduction

Development and launch of large spacecraft, e.g., satellites, require huge investments and are thus limited to large organizations. To make space more available, the use of smaller satellites has emerged. Using smaller satellites reduces mission cost and complexity and has made it possible for science and engineering students to participate in space missions, as well as for emerging and developing countries to launch their own satellites for, e.g., communication and earth observation (Ref 1). For precise adjustment of attitude and orbit, small satellites require a propulsion system with thrust on the micro-Newton scale or less, making it a micropropulsion system.

The use of 3D printing reduces production cost and development time for customized structures, making it well suited for use in the space industry since spacecraft parts are often highly customized (Ref 2). Printing of thrusters for use in micropropulsion, so-called microthrusters, has been demonstrated in polymeric materials (Ref 3) and metals (Ref 4, 5). However, some types of thrusters benefit from operation at high temperatures, often above 1000 °C. This is the case for thrusters in which fuel is combusted at high temperatures, or where pressurized gas is used as the propellant, since the energy content of the gas increases with temperature. Operation at these temperatures disqualifies the use of polymers and most metals. Ceramics, with their generally high melting point, are far more viable.

Systems for 3D printing of ceramics have generally required large investments and have, hence, not been common in laboratory scale experiments or student projects. However, a recently emerged ceramic resin for use in a low-cost benchtop stereolithography (SLA) 3D printer might have the potential to make 3D printing of ceramics more commonly available, e.g., on the laboratory scale (Ref 6).

Traditionally, SLA printing has been used for manufacture of plastic parts through localized curing of layers of a liquid resin containing photocurable monomers. When this resin is exposed to UV light, commonly from a laser, it solidifies. In ceramic SLA printing, ceramic particles are mixed into conventional resins (Ref 7). The printed part then consists of ceramic particles contained in a polymeric binder phase and is a so-called green body. To obtain the final all-ceramic part, the green body is subjected to a firing process in a high-temperature furnace. In this process, the polymeric binder phase is first burnt, after which the ceramic particles sinter into a dense material.

In the printer used in this work, the resin is contained in a tank which is illuminated from below. For each layer to be printed, the build platform is lowered to the bottom of the tank, leaving only a thin gap, corresponding to the thickness of a single print layer, between the bottom and the previously printed layers. The resin layer is exposed to UV light through the transparent tank bottom, whereupon it cures and adheres to the previously printed layer as well as to the tank bottom. After completion of a layer, the platform is raised, peeling the print from the transparent bottom and allowing fresh resin to flow across the bottom of the tank, before the process is repeated for the subsequent layer (Ref 7).

The shape and size of the volume in the resin that is cured during light exposure is affected by the resin composition. For traditional SLA resins, this shape is well-known (Ref 8). However, ceramic particles scatter the light, which broadens the size of the cure spot, reduces resolution and decreases the cure depth (Ref 7, 9). Curing of ceramic resins is thus much more complex and difficult to predict than curing of polymeric ones. Even many commercially available ceramic resins, including the one used in this work, are considered developmental and in need of more characterization (Ref 10).

Ceramic SLA printing has an additional challenge in the process required to turn the green body into the final ceramic part (Ref 11). Burning of the polymer binder must be done carefully to avoid crack formation and swelling (Ref 11). On sintering, SLA-printed ceramics shrink more in the direction transverse to the printed layers (Ref 11,12,13). This causes distortion of the objects if not properly understood and accounted for.

In a previous work on the material used in this study, Xu et al. experimentally investigated its dimensional accuracy, mechanical strength and microstructural evolution. The major issue reported was cracking of the material, which cause was proposed to be the peel-off forces occurring when raising the build platform (Ref 6).

In another work, Nawrot and Malecha envisioned ceramic 3D printing as an upcoming technology when they reported the successful fabrication of microfluidic channels with a minimum cross-sectional dimension of 400 µm. However, they also reported a high porosity of the material, which can be detrimental in fluidic systems. To overcome this problem, co-firing the ceramic with a glaze was performed, but unfortunately not evaluated with respect to its effects on this vital issue (Ref 10).

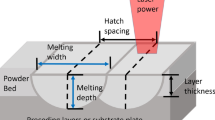
The scale of microfluidics makes the surface finish important. For instance, surface roughness in microthruster nozzles can significantly affect their performance, through frictional losses or due to disturbance of the flow (Ref 5, 14). The surface roughness of SLA 3D-printed objects is affected by process parameters, such as laser power and scan speed, as well as resin properties, including scattering from particles, all affecting the exposure of the resin. However, the main cause of surface roughness is the staircase effect (Ref 15) that occurs from layer-by-layer printing of surfaces at an angle other than 0 and 90° relative to the print direction.

If surfaces are too rough after printing, they can be smoothened through post-processing. Already at macroscale and with plain shapes, the hardness and brittleness of ceramics make the use of conventional machining techniques difficult (Ref 16). At smaller scale, and with the complex geometries offered by 3D printing, it becomes almost impossible, making coating more favorable.

The aim of this study is to explore the potential use of a silica resin for 3D printing of microfluidic systems, in particular microthrusters, focusing on permeability and surface roughness. Printing accuracy, firing shrinkage, surface roughness and permeability of 3D-printed ceramic samples are all evaluated experimentally. Furthermore, glazing of the ceramic is performed and evaluated.

2 Materials and Methods

2.1 Three-Dimensional Printing and Glazing Procedure

All samples were printed using a benchtop SLA printer (Form 2, FormLabs, MA, USA) with a laser spot size of 140 µm, potentially offering a line width nearly as small. A commercial silica-based resin (FLCEWH01, ibid) with a ceramic content of 50 vol.% (Ref 17) was used. (For a detailed study on this material, including x-ray diffraction analysis, see the work by Brackmann et al. (Ref 17)). The default printer settings (PreForm, version 3.26.2, ibid) for the ceramic resin were used, and the layer thickness was set to either 50 or 100 µm. The z-scale factor, which compensates for the additional shrinkage in the direction transversal to the layers, was set to 1.12, as recommended by the manufacturer.

From now on, a designed dimension will refer to a dimension prior to z-scaling, after which it becomes a scaled dimension (for dimensions in the xy-plane, the scaled dimension is equal to the designed one). The scaled model is then printed. Measurements of the printed green body are referred to as green dimensions and measurements after final firing as fired dimensions, Fig. 1.

Fig. 1
figure 1

Nomenclature used for the different dimensions. Dimensional differences are exaggerated for illustrative purposes

Full size image

To ensure adherence of the printed structure to the build platform when printing using this resin, the first few layers are printed with different printing parameters compared to the subsequent layers. To avoid any unwanted effects from this, all parts were printed on support structures.

After printing, the parts were washed by soaking and gently agitating them in two relatively large baths of isopropyl alcohol for about 5 min each. When dry, the parts were carefully detached from the support structures using a scalpel and tweezers.

Samples that were not to be glazed were fired in air at atmospheric pressure in a high-temperature furnace (ECF 20/18, Entech, Sweden), following a scheme after recommendations by the manufacturer, Fig. 2, supported by the thermogravimetric analyses and differential calorimetry by Nawrot and Malecha (Ref 10). Samples that were to be glazed were bisque fired in air at atmospheric pressure in the high-temperature furnace, using a firing scheme suggested by (Ref 18), Fig. 2.

Fig. 2
figure 2

Firing schemes with peak temperatures of 1040 and 1271 °C, respectively. The dwell time at the peak temperature is 5 min in both schemes

Full size image

Glazing was done using a transparent stoneware glaze powder (50030, AB Wilhelm Seeman, Sweden), which was mixed with de-ionized water at a powder-to-water ratio of 1:1.2, measured by weight. Mixing was done first by hand, followed by magnetic stirring for about 30 min. The mixture was then sieved through a sieve with 100-µm opening size, after which the glaze was left in an air-tight container overnight to rest before the first glazing. The glaze was then kept in the container for several weeks for subsequent glazing instances. Before each use, the glaze was stirred by hand until homogeneous.

Two glazing methods were investigated: dip coating and airbrushing. For the latter, two amounts of coatings were explored. Only one side of the sample, the top side, defined in Fig. 3, was glazed.

Fig. 3
figure 3

Schematic of samples on build platform. From left to right: parallelepiped with conical channels, parallelepiped with cylindrical channels and plate

Full size image

For dip coating, the samples were dipped into the glaze for a few seconds. The top side of the samples was facing downwards, and the whole samples were submerged into the glaze. After dipping, excess glaze on the bottom side of the samples was removed using a paper towel, after which samples were left lying flat for drying. When dry, any residual glaze on the back side of the samples was scraped off using a scalpel.

For airbrushing, a hand-held airbrush (Meec Tools art no 082-004, Jula, Sweden) was used. The airbrush was driven by nitrogen gas at an overpressure of 150 kPa. During airbrushing, samples were mounted with the top side oriented vertically. Airbrushing was done normal to the samples at a distance of about 10 cm. The airbrush was swept at about 10-20 cm s−1 across the sample, varying the sweep direction between vertical and horizontal. Five continuous sweeps were done in one round, after which the sample was left to dry for a couple of minutes. The sample was then rotated 90° before the round of five sweeps was repeated. Two procedures, with different amounts of coatings, were evaluated: repeating the five-sweep round either four or eight times. Coated samples were left lying flat for drying.

The dry samples were then glaze fired in the high-temperature furnace at a peak temperature of 1260 °C, which is recommended for this glaze. Heating and cooling were done at a rate of 5 °C min−1.

2.2 Sample Design and Evaluation

Two different types of samples were used in this work: parallelepipeds containing fluidic channels, and square plates. The samples, as well as the nomenclature used, are shown in Fig. 3. The parallelepipeds contained two types of 3-mm long channels going through them. One channel type was cylindrical, and the other was convergent-divergent, creating a conical structure similar to the one found in a microthruster nozzle. These samples were used for the evaluation of size limitations in manufacturing of microfluidic parts and were not glazed. The plates, on the other hand, were studied both with and without glaze. The unglazed plates were used for the evaluation of dimensional properties as well as surface roughness and permeability, whereas the glazed plates were used only for the latter two.

2.2.1 Parallelepipeds with Channels

The parallelepipeds with cylindrical channels had the designed dimensions of 6 \(\times\) 2 \(\times\) 3 mm. Channels were designed with diameters of 10-100 µm, in steps of 10 µm. Channels were divided between two parallelepipeds, such that one parallelepiped contained one channel each of diameters 10-50 µm, and another parallelepiped contained one channel each of diameters 60-100 µm.

The parallelepipeds with conical channels had slightly larger designed dimensions, 12 \(\times\) 3 \(\times\) 3 mm, to fit the structures. All cones had a designed cone half-angle of 20°. The minimum diameter of the cones, at the throat where the two cones meet, was varied from 10 to 100 µm. Cones were split along two parallelepipeds, similar as for the cylindrical channels.

All parallelepipeds were printed with the channel axis parallel to the print direction and with a 50-µm layer thickness. All unique parallelepiped designs were realized as triplicates.

The parallelepipeds were evaluated using light optical microscopy (DVM6, Leica Microsystems, Germany) in both green and fired states using the associated software (Leica Application Suite X, version 3.0.14.23224, ibid).

For parallelepipeds with cylindrical channels, the channel diameter was measured on the top surface by fitting a circle to three approximately 120° separated points selected at the channel edge. Center-to-center distance between adjacent channels was measured for the 20-30- and 40-50-µm pairs, as well as for the 60-70- and 90-100-µm pairs on the other parallelepiped. In addition, the length and width of the parallelepiped were measured on the top surface.

For parallelepipeds with conical channels, the cone throat diameter was measured by fitting a circle to three approximately 120° separated points at the throat. Center-to-center distance between adjacent throats was measured for the 10-20- and 40-50-µm pairs, as well as for the 60-70- and 90-100-µm pairs on the other parallelepiped. The parallelepiped width was measured on the top surface. The length was not possible to measure accurately since it exceeded the field of view of the microscope.

Firing shrinkage was calculated from the dimensions obtained from both green and fired parallelepipeds.

2.2.2 Unglazed Plates

The plates had designed dimensions of 10 \(\times\) 10 \(\times\) 2 mm and were printed at six different designed print angles: 0, 15, 30, 45, 60, 75 and 90° relative to the print direction. Plates of both layer thicknesses (50 and 100 µm) were evaluated. All combinations of print angles and layer thicknesses were explored, and each unique combination was made as a triplicate.

Plate dimensions (width, length and thickness) were measured before and after firing using digital calipers. From these dimensions, the firing shrinkage was calculated.

Due to the scaling factor of dimensions in the z-direction of 1.12, the scaled plate length and thickness vary from the designed dimension with print angle. Basic geometry yields that the scaled plate length, ls, is given by

$${l}_{{s}}=l\sqrt{{f}^{2}{\mathrm{cos}}^{2}\theta +{\mathrm{sin}}^{2}\theta },$$
(1)

where l is the designed length, f is the scaling factor along the z-axis and θ is the designed print angle.

In the same manner, the scaled plate thickness, ts, is given by

$${t}_{{s}}=t\sqrt{{\mathrm{cos}}^{2}\theta +{f}^{2}{\mathrm{sin}}^{2}\theta },$$
(2)

where t is the designed thickness.

The scaling factor is used to compensate for the anisotropic firing shrinkage that gives the reduction in size between the green and the fired dimensions (Fig. 1). Hence, the expected firing shrinkage also varies with print angle. Expected firing shrinkage of the plate length, sl, is given by

$${s}_{\mathrm{l}}=\sqrt{{s}_{z}^{2}{\mathrm{cos}}^{2}{\theta }_{s}+{s}_{xy}^{2}{\mathrm{sin}}^{2}{\theta }_{s}},$$
(3)

where sz and sxy are the firing shrinkage in the z- and xy-directions, respectively, and θs is the scaled print angle, given by

$${\theta }_{\mathrm{s}}={\mathrm{tan}}^{-1}\left(\frac{\mathrm{tan}\theta }{f}\right).$$
(4)

Similarly, the expected firing shrinkage of the plate thickness, st, is given by

$${s}_{\text{t}}=\sqrt{{{s}_{\varvec{xy}}^{2}\text{cos}}^{2}{\theta }_{\text{s}}+{{s}_{z}^{2}\text{sin}}^{2}{\theta }_{\text{s}}}.$$
(5)

Fired plates were examined using x-ray (XT V 130, Nikon, Japan).

Coherence scanning interferometry (CSI) (Nexview NX2, Zygo Corporation, PA, USA) was used to evaluate the surface topography of the plates and to determine their surface roughness before and after firing. An 100x magnification objective and 2x zoom were used, resulting in a field of view of 0.83 \(\times\) 0.83 mm. Data were obtained from three sites (each 0.83 \(\times\) 0.83 mm) on each plate. All analyses were performed using the associated software (Mx, version 8.0.0.3, ibid). The surface average, Sa, was determined over the whole field of view. In addition, the line average, Ra, was determined both in the plate length and width directions at each site.

To compensate for any tilting of the plates during measurement, a plane was fit to the data and subtracted from it before analysis. When evaluating Ra, the mean value along the line was also subtracted from the data, so that Ra was evaluated along the line and not relative to the surface average.

To evaluate the permeability of the material, plates were glued to pieces of polyamide tubing (ID 4 mm and OD 6 mm) using epoxy (Epoxy Rapid, Bostik, Sweden), with their top side facing toward the tubing. The tubing was then connected to a source of compressed nitrogen gas, so that the plate worked as a barrier for it. The pressure and the flow through the plates were measured using a pressure sensor (PTI-S-AA4-32A0-Y, Swagelok, OH, USA) and a mass flow sensor (AWM3150V, Honeywell, NC, USA) each connected to a multimeter (34401A, Hewlett Packard, CA, USA, and 34450A, Agilent, CA, USA, respectively).

Permeability measurements were started at a feed pressure of about 400 kPa, limited by the range of the pressure sensor. For plates where this pressure resulted in a flow rate out of range of the flow sensor, the measurement was repeated at lower pressures until the flow rate was within range of the sensor. The pressure was lowered in steps of 100 kPa down to 200 kPa, then the pressure was lowered to 150, 125, 120 and 110 kPa.

According to Darcy’s law, fluid flow through a porous material is described by

$$Q=\frac{kA}{\mu L}\Delta p,$$
(6)

where Q is the volumetric flow rate, k is the permeability of the material, A and L are sample dimensions, µ is the dynamic viscosity of the fluid and Δp is the pressure drop over the material.

Assuming that all plate samples tested here have the same dimensions,

$$k\propto \frac{Q}{\Delta p}.$$
(7)

This expression can be used as a measure of the permeability of the plates relative to each other.

For the evaluation of plate surfaces using scanning electron microscopy (SEM) (LEO1530, Zeiss, Germany), smaller plates (designed dimensions 3 \(\times\) 3 \(\times\) 2 mm) were used. These plates were coated with a thin (approximately 100 Å) layer of gold–palladium prior to microscopy. Plates of all seven build angles and both layer thicknesses were evaluated, in both green and fired states.

2.2.3 Glazed Plates

Glaze powder, both as-supplied and as-extracted from the glaze after sieving, was evaluated in SEM (LEO1530, ibid).

The plates with designed dimensions of 10 \(\times\) 10 \(\times\) 2 mm were used for the evaluation of glazing. Plates of four different designed print angles: 0, 45, 75 and 90°, were selected and printed with both 50- and 100-µm layer thickness. For each different combination of print angle and layer thickness, all three glazing procedures were evaluated, such that the total number of unique samples was 24.

Plates were visually inspected, unaided as well as with light optical microscopy (DVM6, Leica Microsystems, Germany).

Surface topography and roughness of the glazed plates were evaluated in the same manner as for the unglazed plates. However, for glazed plates, a cylinder was subtracted from the data instead of a plane as this was seen as most appropriate, see discussion. Permeability measurements were conducted according to the procedure for the unglazed plates. Triplicates of each sample type were used for roughness and permeability measurements.

Cross-sections were obtained for one plate of each unique sample configuration by molding the plate in epoxy (Epoxy Rapid, Bostik, Sweden), cutting it with a precision saw (IsoMet 2000, Buehler, IL, USA) and wet grinding it (MetaServ 2000, ibid). All cross-sections were inspected in light optical microscopy (DVM6, Leica Microsystems, Germany), along with the measurement of glaze layer thickness. A selection of cross-sections was also inspected in SEM (LEO1530, Zeiss, Germany), after coating (see 2.2.2).

3 Results

3.1 Parallelepipeds with Channels

Green dimensions in the xy-plane were on average 178 ± 31 µm smaller than designed. On the contrary, green center-to-center distances measured on average 28 ± 12 µm larger than designed. Average shrinkage after firing for all these dimensions was 16 ± 1%.

From microscopy, both channel and throat cross-sections were found to be non-circular, and their boundaries jagged by particles, Fig. 4. All cylindrical channels with designed diameter of 10 µm were clogged after printing. In addition, one channel each of diameter 30, 40 and 80 µm appeared clogged after printing, and one additional channel of diameter 80 µm was found clogged after firing. All throats, on the other hand, were open.

Fig. 4
figure 4

Optical microscopy images of a parallelepiped with cylindrical channels of diameter 60-100 µm (diameter increasing from left to right), green (a) and after firing (b), and of a fired conical channel with a throat diameter of 50 µm (c)

Full size image

Diameters of green and fired channels and throats are presented in Fig. 5 and 6, respectively. Average firing shrinkage for diameters of cylindrical channels was 24 ± 4% and for diameters of cone throats 14 ± 3%.

Fig. 5
figure 5

Average diameter of cylindrical channels in green and fired state, along with standard deviation

Full size image
Fig. 6
figure 6

Average diameter of throats in conical channels in green and fired state, along with standard deviation

Full size image

3.2 Unglazed Plates

Measurements of green plate width, length and thickness showed that dimensions printed purely in the xy-plane (widths of all plates, length of plates printed at 90° and thickness of plates printed at 0°) were smaller than designed, on average 133 ± 59 µm. Dimensions printed purely along the z-axis (length of plates printed at 0° and thickness of plates printed at 90°) were measured larger than designed, on average 239 ± 44 µm. Dimensions with components in both xy- and z-directions suffered from a combination of these effects. See Fig. 7 and refer to Fig. 3 for the definition of dimensions.

Fig. 7
figure 7

Average green dimensions of plates, along with standard deviation. Dashed lines represent, from top to bottom, scaled length (calculated according to Eq. 1), scaled width (equal to designed width) and scaled thickness (calculated according to Eq. 2). Note the break in the y-axis

Full size image

There was no general difference between plates printed with different layer thicknesses.

The average firing shrinkage, Fig. 8, in the xy-plane (calculated from widths of all plates, length of the plates printed at 90° and thickness of plates printed at 0°) was 15 ± 1%, and along the z-axis (calculated from height of plates printed at 0° and thickness of plates printed at 90°) 21 ± 1%. Using these values as the shrinkage factors for the respective axes, the expected shrinkage of dimensions with components in more than one axis was calculated according to Eqs. 3 and 5.

Fig. 8
figure 8

Average firing shrinkage of plates, along with standard deviation. Dashed lines represent, from top to bottom, expected shrinkage in length (calculated according to Eq. 3) and in thickness (calculated according to Eq. 5). Note the two different y-axes

Full size image

During the measurements, a print artifact in the form of a protuberance of excess material at sharp corners printed in the xy-plane was noted, Fig. 9(a). When printing plates at other angles than 90°, the print artifact at the corners resulted in ridges along all edges, Fig. 9(b).

Fig. 9
figure 9

Light optical microscopy image of artifact at a sharp corner printed in the xy-plane, on a plate printed at an angle of 90° (a). Plate printed at a designed print angle of 45°, where the artifact causes walls along all edges (b)

Full size image

Relative permeability measurements, Fig. 10, revealed that 16 out of 21 plates with layer thickness 100 µm were impermeable, but only five out of the 21 plates with layer thickness 50 µm.

Fig. 10
figure 10

Relative permeability of unglazed plates, calculated according to Eq. 7. Note the scale change along the y-axis. Black fill represents impermeable plates and superscripts their number, if more than one. Values to the right along with dashed lines mark the pressure at which the measurements were conducted

Full size image

Measurements of surface roughness, Fig. 11, revealed that most plates have a larger Ra along the length than along the width, even though the difference is not always significant. This difference was also visible in SEM images of the plate, Fig. 12.

Fig. 11
figure 11

Surface roughness for unglazed plates. Error bars represent standard deviation

Full size image
Fig. 12
figure 12

SEM images of unglazed plates printed with layer thickness 50 (a) and 100 µm (b)

Full size image

SEM images also revealed the presence of large open pores in fired plates. Qualitatively, there was less porosity in plates with layer thickness 100 µm compared to 50 µm, and porosity was decreasing with increasing print angle. The pores were evenly distributed across each plate.

In addition to the open pores, higher magnification SEM images, Fig. 13, revealed fine cracks in the fired material.

Fig. 13
figure 13

Fine cracks in a fired plate

Full size image

X-ray imaging of plates, Fig. 14, further revealed that the porous areas in the plates are primarily aligned to the layer interfaces.

Fig. 14
figure 14

Cross-sectional x-ray images of plates printed with layer thickness 50 (a) and 100 µm (b)

Full size image

3.3 Glazed Plates

SEM imaging of the glaze powder, Fig. 15, showed that the powder consists of particles smaller than 50 µm. No difference in composition was seen between the as-supplied and sieved powder samples.

Fig. 15
figure 15

SEM image of glaze powder after sieving

Full size image

With dip coating, the dry, unfired glaze became undulated. Glazing with airbrushing, on the other hand, gave a flat surface.

Due to the fired glaze being transparent, unaided visual inspection and light optical microscopy of the plates were found difficult. However, from light reflections during visual inspection, plates glazed by dip coating or with 8 rounds of airbrushing appeared shiny, indicating a uniform and smooth coating, whereas the surfaces of plates glazed by 4 rounds of airbrushing appeared rough and non-uniform. Intensity images obtained along with the CSI measurements, Fig. 16, confirmed this. Plates glazed by 4 rounds of airbrushing were seen to have only partial coverage. Furthermore, the coverage was highly non-uniform, such that areas with almost no coverage, Fig. 16(a), as well as areas with better coverage, Fig. 16(c), could be found on the same plate. Plates glazed by dip coating or 8 rounds of airbrushing, on the other hand, were covered by a homogeneous and smooth glaze layer.

Fig. 16
figure 16

Intensity images of glazed plates: plates glazed with 4 rounds of airbrushing, resulting in non-uniform coatings with increasing coverage (a-c), plate glazed with 8 rounds of airbrushing, resulting in a fully covering coating (d). Vertical line pattern visible in (c) is from the topography of the underlying plate. Irregularities in (d) are most likely gas bubbles

Full size image

The results from surface roughness measurements, Fig. 17, where plates glazed by 4 rounds of airbrushing had rougher surfaces than other plates, were consistent with these observations. Both 8 rounds of airbrushing and dip coating resulted in a reduction of roughness, where the former gave the smoothest surfaces. CSI measurements indicate that the slightly larger roughness for dip-coated plates is a result of a slight waviness with a spatial periodicity of hundreds of micrometers, rather than smaller irregularities. There was no significant difference in Ra along the length and the width.

Fig. 17
figure 17

Surface roughness, in terms of Sa, of glazed plates. Error bars represent standard deviation. The right graph is a magnification of the left graph for plates glazed by 8 rounds of airbrushing and dip coating

Full size image

For the permeability measurements, all glazed plates were found to be impermeable.

Light optical microscopy of cross-sections, Fig. 18, revealed that plates glazed with 8 rounds of airbrushing or dip coating had glaze layers that were thickest at the center of the plate, i.e., with thickness fading toward the sides. Furthermore, slight color variations in the images reveal that glaze penetrates the printed substrate, however slightly difficult to distinguish.

Fig. 18
figure 18

Light optical images of cross-sections of glazes plates. Plate printed at 0°, glazed by dipping (a), and higher magnification images of the same plate (b), as well as plates glazed with 8 (c) and 4 (d) rounds of airbrushing. Same magnification in (b)-(d)

Full size image

The average glaze thickness for the different glaze procedures, measured at the center of the plate where the thickness was largest, is presented in Table 1. The uncertainty in thickness for glaze layers made by 8 rounds of airbrushing and dip coating was estimated to about ± 30 µm, due to vague interface between glaze and substrate, whereas the uncertainty for glaze layers made by 4 rounds of airbrushing was a few µm. Many of the glazed plates had a slight curvature toward the glazed side, visible both in visual inspection and in light optical microscopy of the cross-sections. The curvature was most prominent in plates printed at 0°. Bubbles were seen in the glaze layer for all plates glazed by 8 rounds of airbrushing and dip coating.

Table 1 Average glaze thicknesses, measured at the center, where the thickness is largest
Full size table

SEM imaging of cross-sections, Fig. 19, confirmed glaze penetration into the substrate material. The penetration depth was about 600 µm, independent of glazing procedure.

Fig. 19
figure 19

SEM images of cross-sections of plates glazed with 4 (a) and 8 (b) rounds of airbrushing

Full size image

4 Discussion

Measurement of cylindrical channel diameters, Fig. 5, shows no correlation between the designed and green dimensions. In previous studies, channels of cross-sectional dimensions down to 400 µm, but unstated length, have been printed properly (Ref 10). Here, this has been drastically improved, as open channels with a diameter of about 250 µm were obtained. However, there is poor correlation between designed and green diameters, most likely as a result of insufficient draining of uncured resin from the channel during or after printing. Small standard deviation is likely a result of measurement uncertainty, mainly from the process of adapting a circle to a non-circular hole, whereas larger deviations may be attributed to uncured resin or particles stuck in the channel, which is probably also the reason for the surprisingly large shrinkage experienced here.

The conical channels, denoted by the diameter of their throats, did not suffer from this problem, most likely because of their wider inlets and outlets, facilitating better drainage of uncured resin than the narrow ones of the corresponding cylindrical channels. Accordingly, these channels exhibit a correlation between the designed and green diameters, Fig. 6. The nonlinearity of this correlation indicates that the green dimension is not solely dependent on the scaled one, but is also affected by resolution limitations of the printer.

The minimum green diameters of about 240 µm obtained for the conical channels are in a range interesting for microscale thrusters. However, not only the diameter is relevant in this application, but also the uniformity of the structures. Many throats were found to be non-circular, and cone surfaces were heavily affected by particles, Fig. 4(c), which could affect gas flow through the thruster, or any microfluidic system.

Green sample outer dimensions in the xy-plane, for both parallelepipeds and plates, were smaller than designed. The size reduction was not proportional to the dimension printed, but rather a constant offset of about 150 µm. Furthermore, the center–center dimensions were not smaller than designed, indicating that the size reduction is not a result of incorrect scaling. One possible explanation is that the intensity of the laser that cures the material is not high enough along the outer rim of the laser spot. Hence, the outermost part of a structure is left uncured, resulting in a size reduction. As mentioned in the introduction, predicting the cure shape in ceramic resins is difficult, and more fine-tuning of the process parameters might be needed.

Another indication that process parameters are not optimal is the occurrence of print artifacts, Fig. 9. These artifacts might not be crucial when printing structures on a larger scale, but might have severe effects in sub-mm structures.

Green dimensions of plates in the z-direction are larger than the scaled dimensions in this direction. However, the number of layers printed, according to the machine, corresponds to the scaled dimension divided by the layer thickness. Hence, each layer printed is thicker than the specified 50 or 100 µm. The reason for this deviation is unknown. Even though the z-axis scaling compensation factor is not intended for the correction of deviations in green dimensions, adjusting this factor might be a viable option in this case. This would also reduce the length of plates with designed print angles 45-75°, which are already smaller than expected. However, this might not be a problem since these lengths experience a smaller shrinkage than expected, Fig. 8. Hence, the final fired dimension, which is the one of actual interest, might be correct. Before any such corrections are made, though, the improper firing shrinkage should be investigated.

The firing shrinkage of 15% observed in the xy-plane is consistent with specifications from the manufacturer, but larger than previously reported experimental values of 9.4-10.8% (Ref 6) and 11.9-12.5% (Ref 12). The firing shrinkage of 21% in the z-direction is smaller than what would be expected from the scaling factor compensation, where a scaling factor of 1.12 in combination with a global shrinkage of 15% would correspond to a total shrinkage of about 24% in the z-direction. However, the shrinkage experienced here is still larger than previously reported 14.37% (Ref 12) and 16.0-17.9% (Ref 6).

The most evident result of too small shrinkage is that the final, fired dimensions are larger than intended. This can be accounted for by re-scaling. Firing shrinkage is a result of de-bindering and densification of the ceramic material. Hence, too small a shrinkage indicates that full densification has not occurred. The porous areas observed with x-ray, Fig. 14, and SEM, Fig. 12, prove this.

As mentioned in the introduction, the occurrence of porous regions and cracks between layers after firing of this material has been reported previously (Ref 6, 10, 11). The cause is thought to be either sedimentation of ceramic particles in the slurry during printing (Ref 13), non-ideal laser exposure throughout the printed layer (Ref 11) or the peeling of the printed structure from the bottom of the curing bath (Ref 6).

These porous regions and the associated anisotropic shrinkage are not unique to this particular material, but are a general phenomenon in ceramic SLA printing (Ref 13). Proper firing should cause these areas to densify and many pores to close, which does not happen in this case. Whether the problem mainly lies in the printing or the firing process remains to be investigated.

The relatively large standard deviation for shrinkage along the z-axis stems from large deviations in the thickness measurements. This is probably due to that the plates printed at 90° have an uneven bottom surface, where the supports have been detached. In addition, the absolute value of the thickness is about 2 mm, and the digital calipers used have a resolution of ± 5 µm. Excluding the thickness measurements and calculating shrinkage from the length measurements only reduce the standard deviation with only a minor change in shrinkage, to 21 ± 0%.

Permeability measurements, Fig. 10, showed that plates printed with 100-µm layer thickness were more often impermeable than plates with 50-µm layer thickness. The main route for gas transportation in the plates is in porous regions, which are most prominent in interlayer boundaries. For a given plate thickness, there are more layers in plates with 50-µm layer thickness. Hence, there are more porous regions. Furthermore, the distance between these regions is smaller, which increases the possibility of connections between pores that can form a continuous route throughout the plate. In addition, plates printed at 90° angle were more prone to be permeable than other plates, independent of layer thickness. In these plates, each porous layer interface covers a large area, which also increases the possibility of connections between pores.

The surface roughness of unglazed plates, Fig. 11, has two components, one from the inherent roughness of the material itself due to the material consisting of particles and one from the surface topography resulting from the layer-by-layer build up. In the plates, the staircase effect will cause steps aligned with the plate width that will then cause an increase in Ra along the length direction. Hence, the staircase effect is the major contributor to the surface roughness in plates where Ra is larger in the length than in the width direction. For plates with layer thickness 50 µm, the difference in Ra between length and width is significant for a designed print angle of 75° only. For 100-µm layers, the difference is significant already at an angle of 45° in the green plates and at 60° in the fired plates. These results are in accordance with the previous theory, stating that this effect is most prominent at slight inclinations and large layer thickness (Ref 19).

However, on comparing surface roughness of plates with different layer thicknesses printed at the same angle, the roughness of plates with layer thickness 100 µm is larger even at a print angle of 0°, where there is no staircase effect. Examination of SEM images, Fig. 12, of plates of both thicknesses printed at this angle reveals that in interfaces between layers can be seen in plates printed with 100-µm layer thickness, but not in plates printed with 50-µm layer thickness. This could be a result of scattering in the ceramic resin, resulting in inhomogeneous exposure of the resin at the large penetration depths that are required for the thicker layers.

Surface roughness at a print angle of 90° is similar for both layer thicknesses. Furthermore, the measured average Ra of these surfaces, of 2.3-2.7 µm, is within the range of 1.58-2.96 µm previously reported for surfaces printed at the same angle with a polymeric resin using the same printer (Ref 20). This was expected since at this angle, the examined surface was in contact with the transparent tank bottom surface during printing, hence can be considered a cast replica of this surface.

For all plates with 50-µm layer thickness, surface roughness is generally larger in fired state than in green. One contribution to this effect is that in the green state, the polymeric part of the resin can fill out voids between the ceramic particles. In fired state, on the other hand, there is no polymer, and the surface roughness is more influenced by irregularities in the shape and structure of the ceramic particles. There might also be a contribution from the open porous areas in the fired material. However, due to blocking of light, the CSI measurement cannot reach into deep valleys. Hence, most of the areas within the deep pores are left unprobed. Actual roughness of the fired plates, accounting for the areas in the pores as well, is larger. However, the roughness measured probably resembles the roughness that could be achieved if a properly fired, dense material is obtained.

For plates with 100-µm layer thickness, the surface roughness is larger in the fired state for print angles of 0 and 90° only. For all other angles, the surface roughness is reduced upon firing, even though the difference is small for designed print angles between 15 and 45°. For plates with designed print angles of 60 and 75°, the reduction in roughness is 14 and 19%, respectively. The reason for the large reduction might be that the roughness on these plates is dominated by the topography due to the staircase effect, and the amplitude of this topography shrinks during firing. This is also consistent with the magnitude of the reduction being on the same order as the firing shrinkage.

For all measurements of surface roughness, there is a relatively large standard deviation in measurements of Ra, especially in comparison with measurements of Sa, since line measurements are heavily affected by local defects, e.g., single particles, on the surface.

All glazing procedures reduced the surface roughness, but the reduction was much larger from dip coating and 8 rounds of airbrushing than from 4 rounds of airbrushing, Fig. 17, as a result of the poor coverage from the latter procedure, Fig. 16. Among plates glazed with dip coating and 8 rounds of airbrushing, there were only small variations, indicating that the original roughness or topography did not affect the roughness after glazing. Taking the coating thickness of 300-400 µm into account, this is reasonable since the coating thickness is magnitudes larger than the surface roughness of the unglazed plates.

Glazing with airbrushing resulted in slightly smaller roughness compared to dip coating, but this is of a magnitude that is probably not relevant in the suggested application. As an example, from simulations of microthrusters (Ref 21), a limit for the acceptable surface roughness for a throat diameter of 1 mm was determined to be 2.4 µm, which is one order of magnitude larger than the roughness obtained in this study.

In CSI measurements of glazed plates, a cylindrical surface was removed as a baseline correction. This gave the smallest roughness, hence should be the most appropriate approximation of the global surface shape.

The issue with light blocking, discussed for the unglazed plates, also affects the measurements of glazed plates. On plates only partially covered with glaze, CSI probes the surface of the glaze only, not the plate surface in valleys in the glaze. Actual roughness of these plates is hence larger.

For the procedures that resulted in uniform and smooth glaze layers, glaze thicknesses of 300-400 µm were obtained. This is large if working on the microscale and would not be appropriate for glazing of sub-mm features. However, by tuning the number of glazing rounds somewhere between the 4 and 8 rounds investigated here, a coating thinner than 300-400 µm, yet being uniform, might be possible to obtain. Further adaption of the glazing process is also needed for glazing of more complex structures.

Nevertheless, even in plates where uniform coatings were not achieved, glazing showed to be a good way to reduce the permeability, since all glazed plates were found impermeable. SEM images of cross-sections, Fig. 19, show glaze penetration into pores in the material, such that no covering glaze layer on the top of the surface is needed for plates to be impermeable. This is useful in applications where surface roughness is not of main importance, but where impermeability is required without influencing sample dimensions or obstructing surface features.

Comparison of cross-sections of plates glazed with 8 rounds of airbrushing to those glazed with dip coating, Fig. 18, showed little difference between the thickness profiles of the glaze layers. Glaze layers were in general thickest at the center of the plates and thinner toward the edges. This was despite the difference seen prior to firing, where dip-coated plates had wavy surfaces from glaze running, whereas airbrushed plates were covered with apparently even layers.

The glazing methods investigated here only work on exposed surfaces. If glazing of interior surfaces is required, either other methods must be explored, such as flowing glaze through a channel, or structures must be built in parts, to then be glazed and assembled, as suggested by (Ref 10). Here, using the glaze as a bonding layer could also be explored.

The large amount of bubbles in the glaze layer could either stem from the glaze itself, or from the 3D-printed material. If the de-bindering process during the bisque firing is insufficient, organic constituents might be left in the material, that are then decomposed into gaseous products upon final firing. More study of the firing processes, both bisque and final, is required to establish the cause for the bubbles.

The curvature of the glazed plates, Fig. 18(a), indicates that there is a shrinkage mismatch between the glaze and the 3D-printed ceramic, possibly caused by a difference either in firing shrinkage or in thermal expansion coefficients. In any coated sample experiencing shrinkage mismatch between substrate and coating, the sample curves toward the material with the largest shrinkage. Here, this indicates that the glaze layer shrinks more than the 3D-printed ceramic. Apart from the difference in shrinkage between coating and substrate, the magnitude of the curvature is also dependent on the stiffness of the materials. Here, the curvature was largest in plates printed at 0°. It is far from unlikely that these plates are the weakest in bending, due to the porous areas in these plates being transverse to the bending direction.

To demonstrate the potential of using the material and glaze explored here in the intended application, glazing of a microthruster nozzle was performed. Optical microscopy revealed a uniform and smooth surface in the exhaust part of the 1400-µm throat nozzle, Fig. 20(a). The exhaust from the nozzle was examined with Schlieren photography (Ref 22), Fig. 20(b), which revealed differences in the exhaust flow between the glazed nozzle and an unglazed nozzle with similar dimensions. These preliminary findings suggest that 3D printing and subsequent glazing of the material explored here might be a viable low-cost method to fabricate ceramic nozzles suitable for use in, e.g., small-scale satellites.

Fig. 20
figure 20

Optical microscopy images of two micronozzle throats (a), and photomontage of optical microscopy images of the nozzles seen from the side, and Schlieren images of the exhausts (b). Top half of each panel is a glazed nozzle, bottom half an unglazed one of similar dimensions

Full size image

As for the shrinkage deviations and the incomplete densification encountered, the former should be compensated for in the design phase in cases where dimensional accuracy is crucial, whereas the latter, although affecting strength and possibly permeability of unglazed structures, should be of less concern in the applications primarily targeted here.

Although the glazing was proven to seal the material printed, and apparently putting it in compression, cracking is still a problem. It is proposed that a material with higher solid loading is developed, and/or that the drying and cleaning steps are studied with crack formation in mind. Using less volatile solvents or a semi-saturated ambient might decrease the stress gradients and transients from drying.

In a wider perspective, this technology will extend the utility of 3D-printed microfluidics from the more or less friendly environments for which it has already been used, to applications of harsh conditions of very high temperatures and corrosive chemicals.

5 Conclusions

In this investigation of properties of 3D-printed silica, microchannels with diameter down to 250 µm were printed, but with poor accuracy. The accuracy was particularly poor for cylindrical channels, which suffered from insufficient drainage of the resin from the channel during printing.

Green dimensions printed in the xy-plane, transversal to the print direction, were found to be smaller than designed, on average 133-178 µm. In the z-direction, on the other hand, green dimensions were larger than scaled dimensions, on average 239 µm. The firing shrinkage was 15-16% in the xy-plane, which is consistent with specifications for this material. In the z-direction, shrinkage was 21%, which is less than expected.

Porous areas along layer interfaces made the material permeable. Plates printed with 50-µm layer thickness were more prone to be permeable than plates printed with 100-µm layer thickness. In addition, all plates printed at 90° print angle were permeable, independent of layer thickness.

Unglazed plates had surface roughness (Sa) between 2.4-20 µm in green state and 4.2-16 µm after firing. The smoothest surfaces were those printed in contact with the optical window of the resin tank. The roughest surfaces were those printed at slight inclinations to the build plate with large layer thickness, consistent with the literature.

To reduce surface roughness and permeability of the material, glazing was explored. Of the three glazing procedures investigated—4 or 8 rounds of airbrushing and dip coating—only the two latter resulted in uniform glaze layers with smooth surfaces. Both these procedures resulted in glaze layers with thickness 300-400 µm. The smoothest surfaces were obtained by glazing with 8 rounds of airbrushing, resulting in Sa below 0.2 µm. Glazing with 4 rounds of airbrushing resulted in non-uniform coatings with thickness less than a few µm. However, all glazing procedures resulted in impermeable plates.