1 Introduction

Transition metal borides, frequently referred to as ultra-high temperature ceramics (UHTCs), exhibit melting temperatures exceeding 3000 °C. This property makes UHTCs particularly attractive for aerospace structures that require thermal protection from extreme operating environments, such as sharp leading edges of hypersonic flight vehicles and reusable atmospheric re-entry vehicles (Ref 1,2,3,4,5,6,7).

Several recent studies focused on densification and microstructural characterization of the UHTCs (Ref 8,9,10,11,12,13). Additionally, extensive research efforts have been directed toward improving the oxidation resistance of the UHTCs (Ref 14,15,16,17,18). These densification and oxidation studies provided important insights in the behavior of the UHTCs and the underlying mechanisms. Whereas ZrB2 and ZrB2-based UHTCs have received greater attention, HfB2 has been reported to exhibit better oxidation resistance (Ref 19,20,21,22,23,24,25). When exposed to air at elevated temperature, HfB2 reacts with O2 forming HfO2 and B2O3. The glassy boron trioxide fills the base of the porous HfO2 scale. The boria remaining on the surface evaporates around 1000 °C. The two reactions are:

$$HfB_{2} \left( s \right) + \frac{5}{2} O_{2} \left( g \right) \to HfO_{2} \left( s \right) + B_{2} O_{3} \left( l \right)$$
(1)
$$B_{2} O_{3} \left( l \right) \to O_{3} \left( g \right)$$
(2)

At 1100–1700 °C, the oxidation resistance of HfB2 can be improved by adding SiC (Ref 3, 17, 18, 22, 26) to form SiO2 upon oxidation. Available B2O3 reacts with SiO2 forming a protective layer of borosilicate glass that covers the surface and fills the pores of the oxide scale (Ref 19, 22,23,24). The two reactions are:

$$SiC\left( s \right) + \frac{3}{2} O_{2} \left( g \right) \to SiO_{2} \left( s \right) + CO\left( g \right)$$
(3)
$$xSiO_{2} \left( {s,l} \right) + yB_{2} O_{3} \left( l \right) \to xSiO_{2} \cdot yB_{2} O_{3} \left( {s,l} \right)$$
(4)

To harness superior properties and excellent oxidation resistance of refractory diborides for engineering applications, we need a predictive model capable or representing all aspects of oxidation. Parthasarathy et al. proposed a mechanistic model to represent the oxidation of the diborides of Zr, Hf and Ti at 1000-1800 °C (Ref 27). The model is capable of predicting the weight change, scale thickness and metal recession for the isothermal oxidation of ZrB2, HfB2 and TiB2. Model capabilities were evaluated by comparing predictions with limited published data. In a follow-on effort, Parthasarathy et al. modeled oxidation of refractory diborides containing SiC (Ref 28). The model was shown to interpret published data for ZrB2-SiC and HfB2–SiC.

The mechanistic models of Parthasarathy et al. have a well thought-out conceptual framework. However, modeling efforts could be significantly strengthened if more reliable and consistent experimental data were available for analysis. At present, model verification is somewhat restricted because the experimental data available in the literature are limited and often inconsistent. Model verification has to rely on data from multiple experiments, thus introducing uncertainties due to variations in experimental setups, test methods, temperatures, material compositions, etc. Moreover, the experimental data available in literature for ZrB2, ZrB2-SiC, HfB2 and HfB2–SiC only provide snapshots of oxidation behavior at specific durations, ranging from a few minutes to 5 h.

This effort aims to provide information on oxidation behaviors of HfB2 and HfB2-20 vol.% SiC at 1500 °C in air in continuous experiments of up to 90-h duration. Another objective of this effort is to gain insight into the effects of sustained compressive stress on oxidation of HfB2-20 vol.% SiC at 1500 °C in air.

2 Experimental Arrangements

2.1 Test Materials

The HfB2 and HfB2-20 vol.% SiC materials used in this work were fabricated using commercially available HfB2 (Cerac, Milwaukee Wisconsin) and SiC (Reade Advanced Materials, East Providence Rhode Island) powders. The HfB2 powder had a purity of 99.5% and a mean particle size of 4.6 μm. The SiC powder was α-phase, 99.9% pure, with particle sizes between 0.03 μm and 3 μm. A Si3N4 grinding media in isopropanol was used to pre-mill the HfB2 powder for 60 h, resulting in an average particle size of 1.3 μm. To process the HfB2 bulk material, a 100 g of HfB2 powder was loaded into a 40-mm graphite die coated with BN and lined with graphite foil. The HfB2 powder was sintered using spark plasma sintering (SPS) with a heating and cooling rate of 50 °C/min and a maximum temperature of 2100 °C. The hold time at 2100 °C was 30 min. A pressure of 40 MPa was applied during heating to 1600 °C and held throughout the remainder of the sintering cycle. The pressure was released to 4 MPa during cool-down to 450 °C. To process the HfB2-20 vol.% SiC bulk material, the appropriate amount of SiC powder by volume was added and the mixture was milled with Si3N4 for 18 h, followed by stirring, drying at room temperature, and dry milling for another 18 h. The mixture was sifted through an 80-mesh screen, and 100 g of the mixture was sintered using the SPS procedure with a 10-min hold time at 2100 °C. Near full density was achieved for both HfB2 and HfB2-20 vol.% SiC. A detailed description of the material processing is given elsewhere (Ref 17, 18, 29).

The sintered HfB2 and HfB2-20 vol.% SiC billets were cut into test specimens utilizing electric discharge machining. After machining, all sample surfaces were polished to a 45-μm finish using diamond slurry to remove surface flaws. Representative as-machined scraps of HfB2 and HfB2-20 vol.% SiC were sectioned and analyzed using scanning electron microscopy (SEM: Quanta 650, FEI, Hillsborough OR) and energy dispersive x-ray spectroscopy (EDS: FEI Quanta 650 with an EDAX Octane Super 60 mm2 detector) to determine the depth of damage and contamination from the machining process. Based on this analysis, the polishing depths for HfB2 and HfB2-20 vol.% SiC were set at 25 and 100 μm, respectively. The nominal dimensions of the test specimens were 6.5 × 6.5 × 19 mm.

2.2 Baseline Oxidation Tests

Baseline oxidation tests of HfB2 and HfB2-20 vol.% SiC were performed at 1500 °C in laboratory air using a Blue M box furnace. During the tests, laboratory air was allowed to naturally circulate in and out of the furnace through several small openings. Two 6.5 × 6.5 × 19 mm specimens of each material were cut into six sections, yielding 12 test samples of each material. The cut ends of each test sample were polished as described above to ensure that all sides had the same finish. For each material eleven test samples were heat-treated, while one test sample was not heat-treated and retained for comparison. The heat treatment (oxidation) times were 0.5, 1, 2, 3, 6, 9, 12, 15, 30, 45 and 90 h. During the baseline oxidation tests, each test sample was resting on an alumina spacer. The surfaces of the oxidized specimens were examined using x-ray diffraction (XRD: Rigaku Ultima IV x-ray Diffractometer, Tokyo, Japan). The open source Rietveld refinement program, MAUD was used to determine phase fractions from the x-ray diffraction patterns. Next the oxidized specimens were sectioned and polished to a 1-µm finish using diamond slurry for examination and chemical analysis. The microstructures were characterized using scanning electron microscopy (SEM: Quanta 650, FEI, Hillsborough OR) together with energy dispersive spectroscopy (EDS: FEI Quanta 650 with an EDAX Octane Super 60 mm2 detector) for elemental analysis.

2.3 Stressed Oxidation Tests

To examine the effects of compressive stress on oxidation, test specimens were oxidized for up to 12 h at 1500 °C in air while being subjected to compressive stress of 50 MPa. The stressed oxidation tests employed a specialized test facility, which integrates a servo-controlled testing machine (MTS model 810) equipped with hydraulic water-cooled wedge grips, a custom-built furnace resistance heated by two MoSi2 heating elements and a MELLEN PS400 temperature controller. An MTS Flex Test 40 digital controller was used for input signal generation and data collection. Two high purity single-crystal YAG (SX YAG) pushrods of 10-mm diameter were used to apply compressive stress to the specimen in the furnace hot zone. The pushrods were mounted in custom-built stainless steel fixtures, which were gripped in upper and lower water-cooled hydraulic wedge grips. Alumina spacers were placed between the SX YAG pushrods and the HfB2-containing test specimen in order to prevent thermo-chemical interaction between SX YAG and HfB2 (Ref 7). Platinum foil was placed between the SX YAG pushrods and the alumina spacers in order prevent bonding during the test. The schematic drawing of the compression test setup is shown in Fig. 1. A detailed description of the experimental facility and of the test setup is given elsewhere (Ref 30,31,32).

Fig. 1
figure 1

Schematic of the compression test setup

Full size image

Effects of compressive stress on oxidation can be assessed by evaluating the growth of oxide scale with time under compressive stress and comparing the results to the unstressed oxidation data. While this approach is conceptually simple, it presents several challenges. It is critical that stressed and unstressed specimens be exposed to identical environmental conditions. Furthermore, it is necessary to eliminate specimen-to-specimen variability due to composition, grain size, etc. A unique experiment was devised specifically to address these challenges. In this test, two test specimens, one stressed and one unstressed, are placed in the test chamber. One standard-sized alumina spacer is replaced by an extra-long spacer allowing for the unstressed specimen to be placed near the stressed specimen. As a result, the stressed and the unstressed specimens are exposed to the same temperature and environment. The stressed oxidation test was interrupted at desired time intervals. Both test specimens were removed from the test chamber and the XRD analysis of the oxidized specimen surfaces was performed. Next a section of each specimen was removed for SEM/EDS examination. Then the stressed oxidation test was resumed with the remaining lengths of both specimens. Specimen-to-specimen variability is thus eliminated by using progressive sectioning of test specimens to assess the growth of oxide scale with time. In this test, the stressed specimen was subjected to compressive stress of 50 MPa. Cumulative exposure times were 5, 8.25, 9.37, 11.75 and 12.27 h. The removed sections were polished and examined with SEM/EDS to evaluate the oxide scale thickness.

Because stressed oxidation test involves repeated cooling and heating of specimens one may query whether the test method affects the oxidation process. To answer this question we also consider oxidation of test specimens during compression creep experiments performed at 1500 °C in laboratory air. Test specimens were loaded to creep stress at the rate of 0.5 MPa/s. Creep stresses varied from 50 to 150 MPa. Once the compression creep test was interrupted the surface of the test specimen was examined using XRD. Then the specimen was sectioned and polished for microstructural characterization with SEM and EDS. Note that alumina spacers included in the load train demonstrated a propensity for early failures under compressive stresses above 50 MPa. Hence sapphire spacers were used in compression creep tests instead (Ref 32). The use of sapphire spacers in the load train permitted compression creep testing at higher loads for significantly longer durations.

3 Results and Discussion

3.1 Experimental Observations

3.1.1 (1) Baseline Oxidation of HfB 2 and HfB 2 -20 vol.% SiC

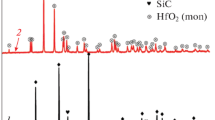
The surfaces of all oxidized specimens were examined using XRD to analyze the crystal structure of the surface scales. Crystallographic Information Files (CIFs) from Crystallography Open Database were used to characterize the x-ray returns. In the case of the oxidized HfB2 specimens, the XRD analysis revealed that monoclinic hafnia (HfO2) was the major crystalline constituent (see a representative XRD pattern in Fig. 2).

Fig. 2
figure 2

X-ray diffraction pattern of the HfB2 sample after oxidation for 18 h at 1500 °C in air; monoclinic HfO2 is the main crystalline constituent

Full size image

X-ray diffraction patterns obtained for the oxidized HfB2-20 vol.% SiC specimens (see a representative XRD pattern in Fig. 3) revealed the presence of HfO2 as the major constituent and HfSiO4 as a minor constituent. Hafnium silicate (HfSiO4, hafnon) is formed from the combination of HfO2 and SiO2, when Si atoms interstitially diffuse into the HfO2 crystal until the solubility limit is attained. Formation of HfSiO4 was previously observed in samples heat-treated at 1200-1400 °C (Ref 33) and at 1600-1800 °C (Ref 17).

Fig. 3
figure 3

X-ray diffraction pattern of the HfB2-20%SiC sample after oxidation for 10 h at 1500 °C in air showing monoclinic HfO2 (o), cubic HfO2 ( +) and HfSiO4 (x) phases

Full size image

All oxidized specimens were sectioned, polished and examined with SEM/EDS to study the morphology of the oxide scales. Typical scanning electron micrographs of the oxidized HfB2 and HfB2-20%SiC samples are presented together with the corresponding EDS line scan analyses in Fig. 4 and 5, respectively. The representative images in Fig. 4 show that HfB2 samples produce the oxide scale composed of a single porous HfO2 layer. This observation is not surprising. It is recognized (Ref 27, 34) that oxidation behavior of HfB2 can be divided into “low” and “high” temperature regimes. Below the transition temperature (generally believed to be about 1000 K) the oxide scale formed on the surface of HfB2 is composed of a glassy outer B2O3 layer and a porous HfO2 layer beneath. The oxidation rate now is limited by the diffusion of oxygen through the protective B2O3 layer making transport of oxygen through the porous HfO2 negligible. At temperatures above the transition temperature, B2O3 evaporates from the oxide scale leaving the porous HfO2 layer (as seen in Fig. 4). The oxide scale is no longer protective. The kinetic model proposed by Parthasarathy (Ref 27) supports the notion of B2O3 evaporation as the cause of the transition from the “low” to “high” temperature regime and the associated loss of protection for HfB2.

Fig. 4
figure 4

SEM micrograph (a) and the corresponding EDS line scan analysis (b) of the HfB2 sample after 1-h basic oxidation test at 1500 °C in air

Full size image
Fig. 5
figure 5

SEM micrographs (a) and the corresponding EDS line scan analysis (b) of the HfB2-20%SiC sample after 1-h basic oxidation test at 1500 °C in air. The oxide scale of the HfB2-20%SiC sample includes (I) SiO2 glass layer and (II) layer of HfO2 with inclusions of Si, O, and C as revealed by EDS

Full size image

Recent studies (Ref 1) showed that at temperatures below ~ 1100 °C SiC additions had little influence on the oxidation behavior of SiC-containing diborides. At these temperatures HfB2 produces an oxide scale composed of B2O3 and HfO2 while SiC remains largely unoxidized. Once the temperature exceeds 1100 °C, B2O3 evaporation takes off and SiC starts to oxidize forming a protective layer of borosilicate glass and resulting in parabolic mass gain kinetics with parabolic rate constant kp ranging from 10–8 to 10–6 kg2/m4·s (Ref 1, 35). The representative images in Fig. 5 also show that HfB2-20%SiC samples oxidized at 1500 °C in this work produce an oxide scale composed of (I) protective borosilicate glass layer and (II) predominantly HfO2 layer as revealed by EDS. Furthermore, the parabolic rate constant obtained from the weight gain measurements in this work is consistent with the values reported in literature.

Sections of the heat-treated samples were examined with SEM/EDS to assess the evolution of the oxide scale with time. Thickness of the oxide scale was measured in 45–118 locations around the perimeter of each section in order to determine the average, standard deviation, and range. Scale thickness measurement includes metal oxide, as well as glass and SiC-depleted regions when present. Results of baseline oxidation tests for HfB2 and HfB2-20%SiC are presented in Fig. 6, 7, 8 and 9. Figure 6 shows typical scanning electron micrographs of the HfB2 samples after oxidation at 1500 °C in air for 1, 9, 45 and 90 h. While Fig. 6a-6c depicts the edges of test samples, Fig. 6d focuses on the center of the test sample. It is evident that the oxide scale grows rapidly, culminating in the complete oxidation of the test sample when exposure time reaches 90 h (Fig. 6d). Starting with exposure time of 9 h, the oxide is no longer small compared to the parent material (Fig. 6b and c). Additionally, we observe corner cracks that in some cases penetrate all the way through the oxide layer. Representative images of the HfB2-20%SiC samples subjected to basic oxidation test at 1500 °C in air for 0.5, 2, 9, 15, 45 and 90 h appear in Fig. 7. It is evident that the addition of SiC decreased oxidation rates by at least an order of magnitude. The oxide scale remains small compared to the parent material. Corner or edge cracks in the oxide scale are not observed. Furthermore, the oxide scale stays attached to the parent material even after 90 h at 1500 °C in air (Fig. 7h). It is noteworthy that the overall morphology of the oxide scales observed in this study is consistent with that reported in literature (Ref 17, 18, 29, 36, 37).

Fig. 6
figure 6

Scanning electron micrographs of the HfB2 samples after basic oxidation test at 1500 °C in air. Test duration is: (a) 1 h, (b) 9 h, (c) 45 h and (d) 90 h

Full size image
Fig. 7
figure 7

Scanning electron micrographs of the HfB2-20%SiC samples after basic oxidation test at 1500 °C in air. Test duration is: (a) 0.5 h, (b) 2 h, (c) 9 h, (d) 15 h, (e) 45 h and (f-g) 90 h

Full size image
Fig. 8
figure 8

Baseline oxidation tests. Oxide scale thickness vs. time for HfB2 and HfB2-20%SiC at 1500 °C in air. Scale thickness measurement includes metal oxide, as well as glass and SiC-depleted regions when present. (a) Time scale adjusted to show oxide scale thickness produced at 5-90 h. (b) Time scale adjusted to show oxide scale thickness produced at 0-5 h. Data for HfB2-20%SiC from Carney (Ref 17) are included for comparison

Full size image
Fig. 9
figure 9

Baseline oxidation tests. Weight gain per unit surface are vs. time for HfB2 and HfB2-20%SiC at 1500 °C in air. (a) Time scale adjusted to show weight gain produced at 10-90 h. (b) Time scale adjusted to show weight gain produced at 0-10 h. Data for HfB2-20%SiC from Carney (Ref 17) and Sevener [368] are included for comparison

Full size image

Figure 8 shows the evolution of oxide scale thickness with oxidation time at 1500 °C for HfB2 and HfB2-20%SiC. Figure 9 depicts a plot of weight gain per unit surface area vs. time. Notably little experimental data on oxidation kinetics of HfB2 and HfB2-20%SiC can be found in published literature. Direct comparison of the results of this study with those in published literature is further complicated by differences in oxidation temperature and time. Carney (Ref 17) reported oxide scale thickness and weight gain for HfB2-20%SiC heat-treated at 1500 °C for up to 1 h. Sevener (Ref 38) reported weight gain for HfB2-20%SiC exposed to 1500 °C for up to 5 h. As seen in Fig. 8 and 9, the results of this work agree well with the limited data reported by Carney (Ref 17) and Sevener (Ref 38). It is evident that the addition of SiC significantly inhibits oxidation. Oxide scale thickness (both average values and associated error bars) as well as weight gain obtained for HfB2-20%SiC are far below those obtained for HfB2.

The oxide thickness data and the weight gain data shown in Fig. 8 and 9 were used to evaluate the oxidation kinetics of HfB2 and HfB2-20%SiC. The parabolic rate constants kp were obtained from the slopes of (i) the square of the weight gain plotted vs. time and (ii) the square of the oxide thickness plotted vs. time. The weight gain kp (kg2/m4·s) and the oxide scale growth kp (m2/s) are shown in Table 1, where the oxidation results from published literature are included for comparison. Note that the parabolic constants calculated in this work are based on the oxidation time of 0.5-45 h, whereas the parabolic constants reported in literature are based on much shorter oxidation times of 1-5 h. In the case of HfB2-20%SiC, the parabolic rate constants obtained in this study are consistent with those reported in literature. In the case of HfB2, the weight gain parabolic rate constant obtained in this study is somewhat lower that that reported by Berkowitz-Mattuck (Ref 39). The differences in density of the test materials, porosity in HfO2 or the presence of the trace impurities may be behind the difference in weight gain kp (Ref 34).

Table 1 Oxidation results for HfB2 and HfB2-20%SiC
Full size table

3.1.2 (2) Stressed Oxidation of HfB 2 -20 vol.% SiC

Baseline oxidation tests revealed that the brittle oxide scale of HfB2 rapidly became detached from the parent material. Thus it was not possible to section the specimen without disturbing the oxide scale. Hence only HfB2-20% SiC specimens were subjected to the stressed oxidation test.

Sections of the stressed and the unstressed HfB2-20%SiC specimens were examined with SEM/EDS to evaluate the evolution of the oxide scale with time. Thickness of the oxide scale was measured in 64–100 locations around the perimeter of each section in order to determine the average, standard deviation, and range. As in the case of baseline oxidation tests, scale thickness measurement includes glass, metal oxide, and SiC-depleted regions when present. Post-test SEM/EDS examination of the stressed and the unstressed HfB2-20%SiC specimens indicated that compressive load had no effect on the overall appearance of the oxidized sections.

Results of the stressed oxidation tests are summarized in Fig. 10, where oxide scale thickness is plotted vs. oxidation time for unstressed specimens and those subjected to compressive stress of 50 MPa. Figure 10 also includes oxide scale thicknesses measured in the baseline oxidation tests (compressive stress = 0 MPa) and in uninterrupted compression creep tests (compressive stress = 50, 75, 100 and 150 MPa). Note that Fig. 10 also includes a prediction obtained using a mechanistic model by Parthasarathy et al. (Ref 28), which is discussed in the subsequent section. It is seen that the oxide scales produced in stressed oxidation tests for the unstressed specimens are close to those obtained for the specimens under 50 MPa compressive stress. Furthermore, Fig. 10 shows little difference between the oxide scales obtained in stressed oxidation tests and the oxide scales produced in compression creep tests at 50-150 MPa as well as those produced in baseline oxidation tests under zero load. Results in Fig. 10 demonstrate that compressive stress of 50-150 MPa has little influence on oxidation of HfB2-20%SiC at 1500 °C. Additionally, good agreement between the data obtained in the stressed oxidation tests and the baseline oxidation tests indicates that repeated cooling and heating during the stressed oxidation tests had little if any influence on the oxidation behavior of HfB2-20%SiC at 1500 °C.

Fig. 10
figure 10

Oxide scale thickness vs. time for HfB2-20%SiC obtained in baseline oxidation tests, stressed oxidation tests and compression creep tests at 1500 °C in air. A comparison between experimental data and predicted oxide scale growth

Full size image

3.2 Modeling

3.2.1 Mechanistic Models for the Oxidation of Monolithic and SiC-Containing Diborides of Hf

The oxidation of HfB2 and HfB2-20 vol.% SiC at 1500 °C in air was also characterized in terms of the mechanistic models developed by Parthasathy et al. for the oxidation of monolithic metal diborides (Ref 27) and SiC-containing metal diborides (Ref 28).

The model for monolithic metal diborides (Ref 27) considered the oxidation of HfB2, TiB2 and ZrB2 at 1000-1800˚C. Model predictions compared well with the limited experimental results found in the literature. This model predicts oxide scale thickness (L), recession (R) and weight change (ΔW) by assuming an isothermal process and slow gas flow conditions. The model assumes that the oxidation reaction of crystalline HfB2 with gaseous oxygen has the stoichiometric form (1). The model also assumes that the air is composed of N2 and O2 only, the surface is a perfect sink for the evaporation of liquid B2O3, and that the transport of oxygen through the metal oxide is negligible compared to the transport of oxygen through the pores of the metal oxide, where the tortuousness of the pores is neglected. For a complete model formulation and a detailed characterization of model parameters the reader is referred to Ref. (Ref 27). For brevity, only the equations for calculating scale thickness, L, recession, R, and the weight change per unit area, ΔW/A, of the oxidized metal diboride are introduced here:

$$L = \sqrt {\frac{4}{5} t D_{{O_{2} }} \left( {\frac{{M_{{ZrO_{2} }} }}{{\rho_{{ZrO_{2} }} }}} \right)\left( {\frac{f}{1 - f}} \right) \left( {\frac{{C_{{O_{2} }}^{a} - C_{{O_{2} }}^{i} }}{1 - q}} \right)}$$
(5)
$$R = L \left( {1 - f} \right)\left( {\frac{{M_{{ZrB_{2} }} }}{{M_{{ZrO_{2} }} }}} \right) \left( {\frac{{\rho_{{ZrO_{2} }} }}{{\rho_{{ZrB_{2} }} }}} \right)$$
(6)
$$\frac{\Delta W}{A} = L \rho_{{ZrO_{2} }} \left( {1 - f} \right) + h f \rho_{{B_{2} O_{3} }} - R \rho_{{ZrB_{2} }}$$
(7)

Here t is time, D is diffusivity, M is molar volume, ρ is density, f is the fraction of the metal oxide that provides a porous and continuous pathway for gaseous diffusion, Ca is the concentration at the oxide scale/ambient air interface, Ci is the concentration at the B2O3 liquid/gas interface, and h is the thickness of the boria layer. The relationship between the thickness of the boria layer, h, and the scale thickness, L, as well as the parameter q are given by:

$$h = qL;\;q = \frac{{\Pi_{{O_{2} - B_{2} O_{3} }} \left( {P_{{O_{2} }}^{i} - P_{{O_{2} }}^{s} } \right)}}{{D_{{O_{2} }} \left( {C_{{O_{2} }}^{a} - C_{{O_{2} }}^{i} } \right) + \Pi_{{O_{2} - B_{2} O_{3} }} \left( {P_{{O_{2} }}^{i} - P_{{O_{2} }}^{s} } \right)}}$$
(8)

Here Π is the oxygen permeability coefficient and P is partial pressure. Although Eq 5-7 indicate the oxidation of ZrB2, they may be generally applied to other metal diborides, provided the appropriate pore fraction, pore radius, thermodynamic data, and physical properties are used.

The model by Parthasarathy et al. for SiC-containing metal diborides (Ref 28) considered the oxidation of HfB2–SiC and ZrB2–SiC at 1200-2200 °C. The model predicts weight gain of the sample, oxide scale thickness, external glassy layer thickness, substrate recession, and depletion layer thickness. Model predictions compared well with the limited experimental results reported in literature for furnace conditions, but not for arc jet conditions. This model uses many of the same assumptions as the previously described model for monolithic metal diborides. However, the addition of SiC requires additional assumptions with regard to the chemical reactions (3) and (4), including the treatment of borosilicate glass instead of just B2O3. A complete model formulation and a detailed characterization of input parameter are given in Ref. (Ref 28). In the interest of brevity, only the equations for modeling recession R, depletion layer thickness l12, oxide scale thickness l23, external glassy layer thickness l3a, and net weight gain, Wg, are introduced below.

$$\frac{{dR_{SiC} }}{dt} = \left| {J_{SiO - 12} } \right| \frac{{V_{SiC} }}{{f_{s} }}$$
(9)
$$\frac{{dR_{{MeB_{2} }} }}{dt} = \frac{{dl_{23} }}{dt} \frac{{V_{{MeB_{2} }} f_{{MeO_{2} }} }}{{V_{{MeO_{2} }} \left( {1 - f_{s} } \right)}}$$
(10)
$$l_{12} = R_{SiC} - R_{{MeB_{2} }}$$
(11)
$$\frac{{dl_{23} }}{dt} = V_{{MeO_{2} }} \left( {\left| {J_{{O_{2} - 32}} } \right| - \frac{3}{2}\left| {J_{SiO - 12} } \right|} \right)\frac{2}{5} \frac{1}{{f_{{MeO_{2} }} }}$$
(12)
$$\frac{{dl_{3a} }}{dt} = \left( {\frac{{dl_{23} }}{dt} \frac{{f_{{MeO_{2} }} }}{{V_{{MeO_{2} }} }} - \left| {J_{{B_{2} O_{3} - vap}} } \right|} \right) + \left( {\left| {J_{SiO - 12} } \right| - \left| {J_{{SiO_{2} - vap}} } \right| - \left| {J_{SiO - vap} } \right|} \right) - \frac{{dl_{23} }}{dt} f_{g}$$
(13)
$$W_{g} = l_{23} \left( {f_{{MeO_{2} }} \rho_{{MeO_{2} }} + f_{g} \rho_{g} } \right) + l_{3a} \rho_{g} - R_{SiC} f_{s} \rho_{SiC} - R_{{MeB_{2} }} \left( {1 - f_{s} } \right) \rho_{{MeB_{2} }}$$
(14)

Here t is time, J is the flux (moles per unit area per unit time), V is molar volume, fS is the volume fraction of SiC in the substrate, fMeO2 is the volume fraction of MeO2 in the 2-3 region, fg is the volume fraction of borosilicate glass in the scale, and ρ is density. The subscripts “vap” and “Me” refer to evaporation and metal, respectively. Full details for modeling many of the variables presented in these equations are given by Parthasarathy et al. (Ref 27, 28).

3.2.2 Model Evaluation

The model capabilities were evaluated by comparing model predictions with experimental results obtained in this work for the long-term oxidation of HfB2 and HfB2-20 vol.% SiC at 1500 °C in air. Model predictions were generated using a numerical code authored by Parthasarathy (Ref 40). The input to the numerical model includes time–temperature history, environmental parameters (i.e., total pressure, oxygen fraction), specimen length and orientation, volume fraction and size of SiC particles. The thermodynamic and kinetic parameters required for modeling were obtained from published literature and built into the code. The reader is referred to Parthasarathy et al. (Ref 27, 28) for further details regarding the input parameters.

Oxide scale measurements obtained in baseline oxidation tests are compared to the model predictions in Fig. 11(a) and (b) for HfB2 and HfB2-20 vol.% SiC, respectively. In the case of HfB2-20 vol.% SiC, model predictions are in good agreement with the experimental data (Fig. 11b). Recall that the model for the oxidation of SiC-containing refractory metal diborides by Parthasarathy et al. (Ref 28) is based on mechanistic models and experimental data from several sources in the published literature. A good agreement between the model predictions and the experimental results obtained in this study invites two conclusions.

  1. 1.

    The model is capable of accounting for the oxidation behavior of the HfB2-20 vol.% SiC for up to 90 h at 1500 °C in air.

  2. 2.

    The experimental results of the present effort are consistent with those in published literature.

Fig. 11
figure 11

A comparison between experimental and predicted oxide scale thickness vs. time for HfB2 (a) and HfB2-20%SiC (b) at 1500 °C in air. Experimental data obtained in baseline oxidation tests

Full size image

Moreover the model predictions agree well with the oxide scale thickness vs. time data obtained in stressed oxidation tests and in compression creep tests for compressive stress of 50-150 MPa (Fig. 10). This result is hardly surprising given that the compressive stress has virtually no effect on the oxide scale growth for HfB2-20 vol.% SiC at 1500 °C in air.

In contrast, oxide scale growth predictions for HfB2 do not compare well with the results of baseline oxidation tests (Fig. 11a). The model (Ref 27) severely under-predicts the oxide scale growth. The experimental scale thickness is three times the predicted thickness after 1 h of oxidation, and 6 times the predicted thickness after 6 h. The discrepancy between the experimental and predicted scale thickness becomes nearly an order of magnitude as the oxidation time reaches 30 h. The most dramatic difference between the experiment and prediction is seen after 90 h of oxidation. During the 90-h baseline oxidation test the oxidation consumes all of the parent material, yet the model predicts an oxide scale of only 281 µm. It is possible that the geometric effects are responsible for the aggressive growth of the oxide scale during 30 and 45 h of oxidation. As the oxidation time reaches and exceeds 9 h, the oxide scale is no longer small compared to the parent material. Furthermore, edge cracks form in the test specimens that in some cases propagate all the way through the oxide layer (see for example Fig. 6b and c). Yet setting aside the data points obtained at 30 and 45 h, which clearly deviate from the expected parabolic trend to higher oxidation rates, a question remains as to why the scale thickness values obtained at 0.5-6 h are so much higher than the model predictions. For example, the baseline oxidation test reports an average oxide scale thickness of 504 μm after 6 h of oxidation, while the model predicts a scale thickness of only 86 μm.

We believe that all assumptions used in model development by Parthasarathy et al. (Ref 27) are consistent with our experimental research. Hence the source of the considerable discrepancies between the model predictions and the experimental results must lie elsewhere. One possibility is the differences between our experimental material and the materials for which the modelers obtained supporting data from literature. The HfB2 used in this work contained about 5% porosity and 2 at.% Zr impurity. These factors could have second order effects, assuming they affect the pore fraction and pore radius of the resulting oxide scale, which significantly influence oxidation rates according to the model. For example, when applied to ZrB2, the model shows that an order of magnitude increase in the pore radius nearly doubles the oxide layer thickness after 1 h at 1500 °C. Similarly, an order of magnitude increase in pore fraction causes an order of magnitude increase in oxide layer thickness.

Variation in model parameters could be another possible source of poor agreement between model predictions and experimental data for HfB2. Variations in model parameters were explored in numerical experiments performed using a computerized model kindly provided by Parthasarathy (Ref 40). Varying time, temperature, velocity, and O2, H2O, SiC, and impurity fractions had little effect on model predictions of oxide layer thickness. The computerized model did not permit variations in the porosity and Zr content of the parent material, or the pore fraction and pore radius of the oxide. These parameters may have considerable effect on model predictions of oxide scale growth, but could not be varied from values assumed by computerized model. These considerations reaffirm the need for experimental studies to explore the effects of the porosity of the parent material, and of the pore fraction and pore radius of the resulting oxide scale on oxidation of HfB2.

The model capabilities were further assessed by comparing weight gain measurements obtained in baseline oxidation tests with the model predictions. Figure 12 charts the weight gain per unit surface area vs. oxidation time for both HfB2 and HfB2-20%SiC. Because it was assumed that no oxidation occurred on the bottom face of test specimens, the area of the bottom face was not included in the calculation. Once again, in the case of HfB2-20% SiC the model prediction compares reasonably well to experimental data. Interestingly, the model prediction also compares rather well to the HfB2 weight gain data. One exception is the data point at 90 h, where the model over-predicts the weight gain by nearly 40%. It is possible that the geometric effects, discussed earlier in regard to the oxide scale growth, are responsible for the model prediction diverging from experimental results as the oxidation time exceeds 30 h.

Fig. 12
figure 12

A comparison between experimental and predicted weight gain per unit surface area vs. time for HfB2 and HfB2-20%SiC at 1500 °C in air. Experimental data obtained in baseline oxidation tests

Full size image

4 Summary and Conclusions

The long-term oxidation behavior of HfB2 and of HfB2-20 vol.% SiC was characterized. Test specimens were oxidized at 1500 °C in air for up to 90 h. Crystal structure of the surface scales was analyzed using the x-ray diffraction. Morphology of the oxide scales was further studied using scanning electron microscopy with energy dispersive spectroscopy analysis. HfB2 produced an oxide scale composited predominantly of porous HfO2, while HfB2-20 vol.% SiC produced an oxide scale composed of a protective outer borosilicate layer and a porous HfO2 layer underneath. Oxide scale growth and weight gain of test specimens with oxidation time were measured in order to assess the oxidation kinetics. For both materials the oxidation behavior was dominated by parabolic kinetics. The parabolic rate constants were calculated using both the weight gain and the oxide scale thickness measurements taken over 45 h. For HfB2 the parabolic rate constants were kp = 2.70 × 10−6 kg2/m4·s and kp = 1.78 × 10−11 m2/s. For HfB2-20%SiC the parabolic rate constants were kp = 1.29 × 10−7 kg2/m4·s and kp = 1.09 × 10−13 m2/s. We further note that while the HfB2 test samples were completely oxidized after 90 h at 1500 °C, the HfB2-SiC samples exhibited oxide scales with an average thickness of 160 µm. Clearly the addition of SiC dramatically inhibited the oxidation of HfB2.

A unique stressed oxidation tests was devised to study the effects of compressive stress on oxidation of HfB2-20%SiC. This test permits simultaneous assessment of oxide scale growth with oxidation time for stressed and unstressed specimens that are exposed to the same environment. The stressed oxidation test showed no measurable effect of 50 MPa compressive stress on oxidation of HfB2-20%SiC at 1500 °C for 12 h. Likewise compression creep tests showed no effect of 50–150 MPa compressive stress on oxidation of HfB2-SiC at 1500 °C for up to 30 h.

The mechanistic models of Parthasarathy et al. for the oxidation of monolithic and SiC-containing refractory diborides were evaluated. These models were formulated based on very limited and often inconsistent experimental data available in published literature. For model verification Parthasarathy relied on snapshots of oxidation behavior taken at short durations ranging from a few minutes to 5 h. Hence it is instructive to assess the model capabilities by comparing model predictions with the weight gain and oxide scale growth measurements collected in this work over 90 h of oxidation.

The model for the oxidation of SiC-containing refractory diborides is generally capable of predicting the oxide scale growth at 1500 °C in air for up to 90 h for HfB2-20% SiC. However, the model for the oxidation of monolithic refractory diborides markedly under-predicts the oxide scale growth for HfB2. Model prediction significantly diverges from the experimental data after only 0.5 h of oxidation. No clear reasons for such disparity could be elucidated, model capabilities regarding the oxidation of HfB2 must be investigated further. In contrast the two mechanistic models are capable of predicting the weight gain during oxidation at 1500 °C in air for HfB2 and HfB2-20%SiC. The model predictions compare fairly well to the weight gain data for both materials for up to 30 h of oxidation. As oxidation time exceeds 30 h, the model prediction for HfB2 diverges from experimental data, while the model prediction for HfB2-20% SiC remains in good agreement with experimental measurements.

While some limitations of the Parthasarathy models were identified, the modeling framework is nonetheless admirable, considering the variety of materials, parameters, unknowns and orders of magnitude it handles.