Introduction

Cold forging is widely used to produce forged parts for various industries. Zhuang et al. (Ref 1) described a cold forging process for spur bevel gears. In their work, the authors compared traditional cold forging and cold orbital forging of a spur bevel gear. The cold orbital forging process for producing bevel gears was also described by Samołyk (Ref 2). Jin et al. (Ref 3) proposed cold orbital forging of components with deep and narrow grooves. In this work, the authors raised a very important aspect of cold forging processes, namely that of tool loading. Ku et al. (Ref 4) proposed a multi-stage cold forging process for producing the outer race of constant velocity joints used in the automotive industry. They replaced the traditional hot forging process performed in seven stages with a 5-stage cold forging process. Compared to the traditional forging method, the new process is characterized by a 7% reduction in input material weight and an 81% decrease in machining time. Pawlicki et al. (Ref 5) described cold upset forging as a technique for joining different materials. In their work, the process of joining aluminum with copper was successfully presented.

Cold forging processes are primarily used for producing steel parts. However, studies are also conducted on cold forging of other materials. In their work, Mandal et al. (Ref 6) described cold rotary forging of Inconel 718 superalloy. The cold rotary forging process proposed by Mandal et al. is not a typical volumetric forging process. In this process, a flange at the end of a tube is formed using a tapered tool. This, however, does not change the fact that it is a cold working process, which poses a great difficulty when using hard-to-form alloys. Aluminum alloys can also be cold forged. Hu et al. (Ref 7) analyzed the effect of a tooling surface on friction conditions in cold forging of Al608 alloy. Copper alloys are other materials formed by cold forging processes. Chen et al. (Ref 8) presented a multi-stage cold forging process for a H68 brass cylindrical shell part with a deep blind hole.

Cold forging processes are characterized by very high tool loading, which often prevents correct implementation of the developed technological processes. Ku and Kang (Ref 9) optimized the shape of an inner race for the automotive industry to minimize tool loading during forging. In addition, in order to reduce tool load during cold forging, the input material is heat treated (soft-annealed) prior to the forging process, which leads to reduced yield stresses. Optimal spheroidize annealing of low-carbon steel for cold upsetting was described, among others, by Gul et al. (Ref 10). Matsumoto et al. (Ref 11) proposed a method for reducing axial forging load in cold forging by introducing low-frequency torsional oscillation of the lower die. An important aspect of reducing tool load in cold forging is the selection of suitable lubrication. Phosphatizing is used in cold forging processes, and it consists of coating input material with phosphorus compounds to reduce the friction coefficient, as described by Ku and Kang (Ref 12). In their other work, Ku and Kang (Ref 13) focused on the problem of heat treatment of tools for cold forging. A proper heat treatment of high-speed steel tools ensures their tensile strength of 4200 MPa and yield strength of 3000 MPa.

Hollow elements may be manufactured using plastic working methods, machining and casting. In the case of machining, the obtained elements are of the highest dimensional accuracy. The efficiency and material yield, however, are low. Casting allows one to obtain products of high dimensional accuracy and efficiency, but the life of the element is short. Plastic working technology allows for high efficiency and long life of the formed elements. Monitoring the changes to the inner hole as well as stability loss of the shape during forming cause numerous problems in the plastic working process. Plastic forming of hollow elements from tube-shaped billet can be performed using the following methods: forging on swaging machines, cross-wedge rolling, extruding, forging, hydroforming and rotational compression (Ref 14,15,16,17,18,19).

Lately a few interesting processes of manufacturing hollow elements were developed. One such method is rotational compression, in which a tube element is formed with three rotating rolls, which simultaneously move in the radial direction and compress the element (Ref 20). Another method is rotational crushing, in which the steps of the shaft are formed with rotating rolls that move along the axis of the formed element. The subsequent steps of the shaft are created as a result of changes to the thickness of the tube wall (Ref 21). The process of three-roll skew rolling is performed on CNC rolling mills. The rolls move in the radial direction in accordance with the selected program, which allows one to manufacture steps on shafts with various diameters. The formed element is moved by a special handle, the movement of which is synchronized with the forming rolls (Ref 22). All of these forming methods require the use of special and expensive machines.

On the basis of the literature available, it can be stated that in the process of manufacturing hollow shafts from tube billet a mandrel can be employed, but it is not a necessity. The mandrel allows one to control the dimensions of the hole in the forging and prevents uncontrollable crushing of the element during forming. The technologies described above require special machines. Only the forging technology can be performed using universal machines. Additionally, in order to obtain a correct hole in the forging, a mandrel ought to be used. It was therefore assumed that the simplest and cheapest method would be the process of forging with a mandrel. The article presents a new technological process of forging hollow elements, aiming to minimize material usage. The main objective of the research was to develop and verify an effective process of forging a hollow sleeve using conventional machines such as press. The article presents: the concept of forging hollow elements, results of numerical simulations of such process for EN 42CrMo4 grade steel (appropriate material) as well as experimental verification using the model material EN AW-6060.

Manufacturing Process for a Rotary Sleeve

This paper describes a manufacturing process for rotary sleeves, which are used in mining cutting systems and harvesters for removing asphalt pavements. The task of a rotary sleeve is to enable a quick and easy attachment of a cemented carbide rotary cutter in the handle (Ref 23). The rotary sleeve under study is shown in Fig. 1. A schematic design of the proposed manufacturing process is shown in Fig. 2. The input material is first subjected to drilling. After that, the thick-walled sleeve is subjected to roughing and finish turning. Finally, the obtained detail is subjected to hardening and tempering. In this manufacturing process, the technological discard weighs approx. 3.5 kg, which amounts to 74% of the total weight of the input material. Figure 3 shows a schematic design of the new manufacturing process for a rotary sleeve. The novelty of the proposed manufacturing process consists of using a different input material and manufacturing methods. Drilling and rough turning operations are replaced by extrusion and forging. Figure 4 shows the dimensions of the tube and the forged part after the final forging operation. In this manufacturing process, a tube section is used as the input material subjected to forging in 4 operations. Firstly, a tube section is subjected to extrusion in order to reduce the wall thickness of the tube together with the outside and inside diameters of the shank. Following the extrusion operation, the inside diameter of the head is reduced while the wall thickness and the outside diameter are increased. The head is upset into temporary tapers in two subsequent operations. In the last operation, the final shape of the flange is formed. During extrusion and forging operations, the inside hole of the workpiece is sized with the use of a pin. After forging, the workpiece is subjected to roughing and heat treatment. Although the new manufacturing process entails a greater number of operations, the four forging operations are less time consuming than drilling and roughing combined, which means that the new solution is characterized by a shorter duration. In addition, the purchase cost of a tube is lower than that of a rod due to the tube’s smaller weight. In the new manufacturing process, the discard weighs 0.33 kg, which amounts to merely 21% of the input material weight. Implementation of the new manufacturing process will hence enable a material saving of over 3kg.

Fig. 1
figure 1

Rotary sleeve—isometric view

Full size image
Fig. 2
figure 2

Manufacturing process for a rotary sleeve

Full size image
Fig. 3
figure 3

Proposed new process for manufacturing a rotary sleeve

Full size image
Fig. 4
figure 4

Geometry and dimensions of: (a) a tube, (b) a rotary sleeve

Full size image

Methods and Materials

Numerical Modeling and Experimental Tests

The developed forging process for a rotary sleeve was modeled numerically using the simulation software DEFORM 3D ver. 11.0. The software was used and validated many times by the authors in their previous studies (Ref 24, 25). The modeling was performed for a forged part made of the appropriate EN 42CrMo4 steel. The material was modeled as an elastic-plastic object. The tools were modeled as rigid objects. The velocity of the punch was set to 1.6 mm/s according to the capabilities of the testing machine. The input material was discretized using 150,000 tetragonal elements. The forging process was simulated in cold working conditions, with the temperature of the input material and the tools being equal to 20 °C. The conditions of tool—billet contact were described using the shear friction law model, expressed by the following dependency: τ = k⋅m, where: τ—friction shear stress, k—ultimate shear strength, m—friction factor. Friction factor in this model in this model remains in the range 0 < m < 1. Friction stress depends on the contact conditions, determined by the friction factor m and material properties k. The numerical results were verified using the material model of soft-annealed aluminum alloy EN AW-6060.

Upsetting, extrusion and forging tests were carried out on the Instron 1000HDX testing machine. The extrusion and the forging of the tube into temporary tapers were carried out with the use of 1:2 scale tools shown in Fig. 5. Owing to the use of a material with lower yield strength, the cost of tooling used in the tests was much lower because the tools were made of hardened and tempered EN C45 steel. Geometrical models of the analyzed processes are given in Fig. 6. This figure shows only one of the employed forging patterns because the two following patterns only differ with respect to punch geometry.

Fig. 5
figure 5

Test equipment: (a) working space of the testing machine, (b) tool set used in experiments

Full size image
Fig. 6
figure 6

Geometrical models of the analyzed processes: (a) extrusion, (b) forging

Full size image

Mechanical Properties

In the research, typical methods of determining flow curves and friction factor were applied. The choice was aided by similarity of the stress state in the tests and the analyzed forging process. For this reason, upsetting test was selected.

Friction conditions were determined in the process of upsetting a ring-shaped sample. Initial dimensions of the ring samples were as follows: ∅20 × ∅10 × 7 mm. Ring samples were lubricated and upset to 4 mm in a universal testing machine. The value of the friction factor m was determined on the basis of a comparison of selected dimensions of samples obtained in real conditions by the means of FEM numerical modeling. Numerical simulations were performed for variable friction conditions to the point of obtaining the greatest coherence of dimensions of samples obtained experimentally and with FEM. Based on the conducted tests, it was assumed that the process would use lubrication with mineral oil and an addition of molybdenum disulphide and that the friction factor would be set equal to m = 0.16. The results published in the article (Ref 26) indicate that the obtained value of the friction factor 0.16 is possible.

Flow curves for EN 42CrMo4 grade steel and EN AW-6060 aluminum alloy were obtained in the test of upsetting cylindrical samples. Steel samples were of the following initial dimensions ∅ 15 × 18 mm. Steel samples were subjected to upsetting to 5 mm. In the case of aluminum samples, the initial dimensions were ∅25 × 30 mm and were upset to 15 mm. The spheroidizing of EN 42CrMo4 steel was carried out in the following conditions. Firstly, the material and the furnace were heated to the soaking temperature; the material was then held at 720 °C for 9 h; finally, the material and the furnace were cooled to ambient temperature. The soft annealing process of EN AW-6060 aluminum alloy was carried out at 415 °C for 5 h. A comparison of the flow curves of EN 42CrMo4 steel and EN AW-6060 aluminum alloy is given in Fig. 7. The samples after tests are shown in Fig. 8. EN AW-6060 was used for physical modeling of the behavior of EN 42CrMo4 grade steel. The yield point of the EN AW-6060 aluminum alloy is smaller than in the case of EN 42CrMo4 grade steel. Using a material with a low yield point for the research allows one to limit the cost of pre-implementation trials. It is possible to use tools made of construction steel without heat treatment for the tests. Additionally, these tools can be made monolithic and do not require compression rings. Lower horsepower machines can be used to perform the tests. Conducting tests using model material also helps to identify problems were not observed in numerical FEM modeling. Strain hardening can be observed for both materials. The flow curves of both materials are described by the Hollomon equation expressing the following relationship: σ = Kεn, where σ is the flow stress, MPa, ε is the true strain, K is the material constant, MPa, n is the strain-hardening exponent. Mechanical properties of the material used in the numerical simulation and of the model material used in the experimental tests are given in Table 1.

Fig. 7
figure 7

Stress–strain curves of EN 42CrMo4 steel and aluminum EN AW-6060

Full size image
Fig. 8
figure 8

The samples after tests: (a) steel sample after upsetting for flow curve, (b) aluminum sample after upsetting for flow curve, (c) ring sample after upsetting for friction determination

Full size image
Table 1 Mechanical properties of the tested material
Full size table

Results and Discussion

Geometry of Forged Parts

Figure 9 shows the changes to the shape of the workpiece in subsequent operations. Based on the shape of the rotary sleeve, it can be concluded that the extrusion and forging processes proceed correctly. Both the external and internal shape of the forged part are satisfactory. The most dangerous phenomenon that may occur when forging hollow parts is lack of contact between the workpiece inner wall surface and the sizing pin, which may cause wrinkle occurrence. No inner wall surface defects of forged parts can be observed in the forging cases analyzed by the finite element method. A more detailed picture of the inner wall surface will be given upon analyzing the contact surface between the workpiece and the pin.

Fig. 9
figure 9

Shape of the workpiece in individual operations: (a) front view, (b) axial section view

Full size image

Figure 10 shows the way in which the inner surface of the workpiece wall adheres to the pin during subsequent operations. After extrusion, the inner surface of the upper part of the workpiece is in contact with the pin over the entire height of the head. It can be observed that after forging operation 1, the material in the central part of the head loses contact with the sizing pin. The no-contact zone between the workpiece and the pin has the maximum depth of x = 0.18 mm while its maximum height is y = 12.8 mm. Given these dimensions of the gap between the pin and the workpiece wall inner surface, there is a minimal risk of material buckling in subsequent operations and thus of wrinkle occurrence. This results from the small depth of the gap and its high height, which means that the y/x ratio is very high and amounts to 71.1. With such slenderness of the gap, the risk of wrinkle occurrence at this stage of the manufacturing process is minimal. This is confirmed by the extent of the contact zone in subsequent operations. The coefficient y/x has been proposed to describe the buckling of the material. It was also stated that in the case when the coefficient reached 71.1 the risk of buckling is insignificant, since after another forging procedure the material adhered to the mandrel better. The authors researched this parameter, however, it is difficult to determine the critical value of this parameter. It is, to a great extent, dependent on the level of upsetting in the subsequent forging operations and therefore, the number of forging operations. After forging operation 2, the extent of the no-contact zone between the workpiece and the pin is clearly reduced in the central part of the head. In this case, it was extremely difficult to measure the no-contact zone due to its small size. However, after the third forging operation, the workpiece is in contact with the pin over the entire height of the workpiece head. Thus, it can be stated that the initial non-adherence of the material to the pin was eliminated in subsequent forging operations.

Fig. 10
figure 10

Workpiece-pin contact in extrusion and forging operations

Full size image

A general view of forged parts obtained in the experiments is shown in Fig. 11(a). The forged parts do not have any disqualifying surface defects. Numerical results were verified by comparing the dimensions of parts obtained from FEM and experimental tests. The dimensions of the obtained parts in experiment were measured with an electronic caliper with a measurement accuracy of 0.01 mm. After the execution of each forging and extrusion operation, 5 measurements of the defined dimensions were made. They were repeated for 5 forgings, making a total of 25 measurements of each dimension. The results are given in Table 2. Measurement points are marked in Fig. 12. The appropriate part dimensions were scaled 1:2. In addition to that, the dimensions of the forged parts obtained in later operations were compared with those of the CAD model. The experimental dimensions show a good agreement with the FEM results. The dimensions of the appropriate part only slightly differ from those of the CAD model. The differences are not very significant and can be eliminated by machining allowance. Diametral dimensions of the forging from experimental testing are greater than the assumed dimensions (CAD). It is supposedly caused by elastic displacement of the tools used in experimental testing. In the case of numerical calculations, the tools were perfectly rigid that is without elastic displacement. Only the d3 dimension is smaller than assumed. Diameter d3 is formed in the last stage of forging. Due to this fact, if other dimensions of the forging increase, there is not enough material to obtain a correct outline of the head of the forging. Height dimensions of the forging obtained in the experiment are also bigger than the dimensions assumed in CAD. In this case changing of the dimensions results from elastic displacement of the frame of the testing machine. Correct height of the forging will depend mostly on the stiffness of the machine. Forged parts obtained in individual forging operations are shown in Fig. 11(b). Inside the hole one can observe spots (marked with a red circle) where the inner surface of the hole does not stick to the pin. After extrusion one can notice a trace on the hole surface, which proves that this region of the material did not adhere to the sizing pin surface. This situation differs from that illustrated in Fig. 10 where the material is in contact with the pin over the entire height of the head. This situation can only be explained by the fact that during extrusion an air cushion is formed and thus prevents the tool cavity from being filled completely. A scheme illustrating the air cushion formation is given in Fig. 13. The air cushion effect was impossible to include in the FEM analysis, hence the material ideally adhered to the mandrel following the extrusion operation. In the experiments, however, the air cushion effect occurred and constrained the flow of the material toward the mandrel. Since the air cushion effect was not taken into account in numerical modeling, the experimental findings differ from the numerical results. The differences between the numerical and experimental results stemming from neglecting the air cushion impact can be observed in Fig. 10 and 11(b). It can be noticed that at first the material tightly adheres to the pin in the region of the die and punch, but then, in the central part of the workpiece a closed air cushion is formed preventing complete filling of the tool cavity in subsequent stages of the extrusion process. This slight non-adherence of the material in the first operation may have a great impact on successive operations. In this case, the tools, particularly the pin, should be provided with a venting system to prevent air cushion formation. In subsequent operations, once can observe a trend similar to that identified in the FEM simulation—namely, the extent of the zone in which the material is not in contact with the pin visibly decreases as the process proceeds. A magnified view of the material’s non-adherence to the pin in the final forged part is shown in Fig. 14. The most important information provided by this figure is that this defect is not overlap and that it only occurs in the region of the hole. In the final forged part, the maximum depth of material non-adherence to the pin wall is 0.23 mm. In the case of the appropriate part, this dimension can be twice as high due to the applied process scale. Nevertheless, this value is so low that it has no effect on the forged part quality.

Fig. 11
figure 11

Forged parts produced in experimental tests: (a) general view, (b) sectional view

Full size image
Table 2 Comparison of the dimensions of produced parts
Full size table
Fig. 12
figure 12

Schematic of measurements of forged parts

Full size image
Fig. 13
figure 13

Schematic illustrating the phenomenon of air cushion formation in the tool cavity

Full size image
Fig. 14
figure 14

Magnified view showing the no-contact zone between material and pin in a forged part

Full size image

Stress and Strain States

Figure 15 shows the distribution of effective strains after individual operations. Following the extrusion operation, increased strains can only be observed in the shank where the outside diameter and wall thickness were reduced. In the following forging operations, the strains in the shank do not change to any significant degree. During forging of the workpiece into temporary tapers, clearly higher strains are located at the lower diameter of the taper. The wall thickness in this region is significantly increased, which leads to higher strains. These can also be observed in the region where the shank and the flange are attached, along the temporary radius between these zones. One can also notice higher strains inside the workpiece, in the region where the material is not in contact with the pin (Fig. 10). In every successive forging operation, one can observe a clear increase in the strains located in the no-contact zone. At the beginning, the material clearly does not adhere to the pin wall (Fig. 10, forging 1) and flows radially away from the pin. In subsequent forging operations (Fig. 10, forging 2 and 3), the material flows radially in the opposite direction, i.e., toward the sizing pin. This pattern of material flow may cause an additional increase in strains generated in this region. The adopted hypothesis can be confirmed by the distribution of strain tensor components in the polar coordinate system, as shown in Fig. 16. The polar coordinate system was defined in such a way that the ‘Z’ axis would overlap with the axis of the workpiece. Fig. 16(a) shows the distribution of radial strains, with the highest radial strains located in the region where the material is not in contact with the sizing pin. This region is also characterized by higher axial strains, as shown in Fig. 16(c). The observed distribution of radial and axial strains proves that this type of material flow may lead to wrinkle occurrence in this region. As shown in Fig. 16(b), the distribution of circumferential strains is typical for material upsetting in the punch. The highest circumferential strains are located on the outside surface of the head. The circumferential strains are significantly lower than the radial and axial strains.

Fig. 15
figure 15

Distribution of effective strains

Full size image
Fig. 16
figure 16

Strain tensor components: (a) radial strains, (b) circumferential strains, c) axial strains

Full size image

Figure 17 shows the distributions of effective stresses in individual forging operations, as determined according to the von Mises hypothesis. These distributions show the effective stresses toward the end of individual operations. In the extrusion operation, the maximum effective stresses are located only in the deformation zone. In all forging operations, the maximum stresses are located in the shank that is placed in the die. In other regions, i.e., in the upper part of the workpiece head, the effective stresses are considerably lower. It can also be observed that the workpiece head is upset incrementally, i.e., its upper part is deformed first, and then the lower part of the head is subjected to deformation. This is proven by the fact that in forging operations 2 and 3, the stresses in the upper part of the head are lower than the yield point. The material behaves as a rigid object in this region. In the final operation, one can observe a local increase in the effective stress in the region that is most prone to wrinkle occurrence. The local concentration of stresses in this region may result from the undesired material flow pattern which may, in turn, cause wrinkling.

Fig. 17
figure 17

Distribution of effective stresses (MPa) according to the von Mises hypothesis

Full size image

Fracture Criterion

The FEM simulation software employed in this study makes it possible to predict material cracking based on different types of criteria. One of the most widely used criteria in metal forming is the empirical Cockcroft–Latham ductile fracture criterion expressed as: \(C_{C - L} = \mathop \smallint \limits_{0}^{\varepsilon } \frac{{\sigma_{1} }}{{\sigma_{i} }}{\text{d}}\varepsilon\), where σ1 is the maximum principal stress, σi is the effective stress, ε is the effective strain, CC-L is an fracture indicator for Cockcroft-Latham fracture criterion. According to this criterion, material damage occurs when the value of CC-L exceeds the critical value for a given material, Ccritical. The critical value can be determined by the equation using material elongation at break A (Ref 27): \(C_{{{\text{critical}}}} = 1,5\ln \left( {1 + \frac{A}{100}} \right)\), where A is the elongation of material at break expressed in %. Obtained distributions of the Cockcroft-Latham criterion across the rotary sleeve in individual forging operations are given in Fig. 18. As the process continues, the fracture indicator CC-L for Cockcroft-Latham criterion reaches higher and higher values. The highest values of the fracture indicator CC-L are concentrated in the cylindrical region part of the workpiece head. In this region, the highest increase in the diameter of the workpiece occurs when compared to the outside diameter of the stock material. As a result, this region is subjected to the action of tensile circumferential stresses that may cause cracking. The region of the highest i fracture indicator CC-L values coincides with the location of the highest circumferential strains (Fig. 16b). The distributions of the circumferential strains and the ductile fracture criterion indicate the presence of undesired tensile circumferential stresses in this region. Based on critical value equation and the elongation A = 23.5% for EN 42CrMo4 steel, the critical value of fracture indicator for Cockcroft-Latham criterion was determined, amounting to Ccritical = 0.32. Based on the obtained fracture indicator for Cockcroft-Latham ductile fracture criterion and the critical value of this criterion, it can be claimed that the proposed manufacturing process is free of crack formation. The maximum value of the fracture indicator for fracture criterion obtained in FEM was CC-L = 0.2 and is lower than the critical value Ccritical = 0.32.

Fig. 18
figure 18

Distribution of the normalized Cockcroft-Latham ductile fracture criterion

Full size image

Normal Pressures

Normal pressures are important in terms of forging tool loading. They determine the selection of tool material type and tool design. Normal pressures and their values are of particular significance in cold forging processes in which surface pressures may exceed 2500 MPa (Ref 28, 29). Figure 19 shows the distribution of contact pressures toward the end of individual operations, i.e., when the forming forces are the highest. In the manufacturing process, under study the maximum normal pressures do not exceed 2000 MPa. In the extrusion operation, the highest pressures (2000 MPa) are generated in the conical part of the extrusion die. The pressures in the region of the container are significantly lower and do not exceed 1250 MPa. In the forging operation 1, the highest pressures (2000 MPa) are located at the bottom of the punch. This results from the fact that during upsetting the material is not in contact with the punch bottom over its entire area. In this forging case, high normal pressures are also located on the surface of the pin sizing the inside hole of the part. In forging operation 2, the tool loading is much lower than in forging 1. In forging operation 3, the normal pressures amount to at least 2000 MPa and definitely cover the biggest region of the tools. In this forging operation, the pressures increase in the region of the die where the shank is located.

Fig. 19
figure 19

Distribution of normal pressures (MPa) toward the end of individual operations

Full size image

Forging Forces

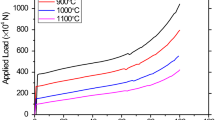
Obtained characteristics of the forces in the analyzed extrusion and forging operations are presented in Fig. 20. The correctness of the force progression obtained from FEM and experiments was examined by obtaining the determination coefficient R2. The results are presented in Table 3. Qualitative compliance of the characteristics obtained from FEM and experimental testing is satisfactory mainly in the case of forging. During the first forging operation, the compliance of force progression reached 85%. In the second forging operation the highest, 94% compliance was obtained, whereas in the third operation—90%. The FEM and experimental results show a satisfactory qualitative agreement predominantly in the case of forging operations. As for extrusion, the FEM and experimental extrusion forces clearly differ at an early stage of the operation. In the case of extrusion force distribution, the lowest compliance was obtained, mainly 72%. The plot in Fig. 20 reveals that in the extrusion operation, the container chamber is filled much faster in the experiment than in the FEM simulation. Naturally, this may result from a different nature of material flow that was confirmed by the results given in Fig. 10 and 11. Another cause of this situation may be the fact that in real conditions an air cushion is formed, which accelerates the filling of the container chamber. The experimental and numerical forces in the forging operations show a much greater qualitative agreement. In order to assess quantitative agreement of the forging and extrusion forces, a comparison was made between the forces simulated by FEM with those estimated by physical modeling. For this purpose, the following formula was used: \(F_{e} = \lambda F_{m} s^{2}\), where Fe is the maximum estimated force, λ is the coefficient describing similarity between the flow curves of the appropriate material (EN 42CrMo4 steel) and the model material (aluminum EN AW-6060), Fm is the maximum force obtained in physical modeling for aluminum EN AW-6060, s is the geometric scale of a given problem. The flow curve similarity coefficient λ was determined based on the data given in Fig. 5, and the following relationship: \(\lambda = \frac{{\mathop \smallint \nolimits_{0}^{\varepsilon } \sigma_{{{\text{42CrMo4}}}} d\varepsilon }}{{\mathop \smallint \nolimits_{0}^{\varepsilon } \sigma_{{\text{AW - 6060}}} d\varepsilon }}\). A comparison of the maximum forces obtained in individual operations is given in Table 3. This table presents the maximum force determined in physical modeling (Fm), the maximum force in the forging of a 1:1 scale rotary sleeve made of EN 42CrMo4 steel that was estimated by physical modeling (Fe), and the maximum force in the forging of a 1:1 scale rotary sleeve made of EN 42CrMo4 steel that was simulated by FEM (Ffem). The forces in all the analyzed operations determined by physical modeling are underestimated compared to the FEM results. In the case of forging operations 1 and 2, the underestimation of the force values is quite significant and amounts to 18 and 11%, respectively. The underestimation may result from stopping the forging press too early, which can be confirmed by the fact that in forging operations 1 and 2, the experimental height h1 is evidently higher than that obtained by FEM (Table 2). In extrusion and forging operation 3, the agreement between the results is very high, and the error does not exceed 1%. Differences in the values of forging forces for numerical and physical modeling will also result from elastic displacement of the body machine. In the case of deflection of the frame, the punch will not obtain the desired location in relation to the forging and as a result the pressure on the forging will be less significant. In the case of forging in the final phase, the force on the punch increases vertically very rapidly with the minimum stroke of the punch. Due to this fact even a very insignificant deflection of the machine or imprecision of stopping the punch would have a huge influence on the forging force. In the analyzed case, forging forces from physical modeling are less significant than the FEM-determined forces, which indicates elastic displacement of the body of the testing machine.

Fig. 20
figure 20

FEM and experimental characteristics of extrusion and forging forces

Full size image
Table 3 Comparison of data concerning extrusion and forging forces
Full size table

Conclusions

In this study, the proposed manufacturing process for rotary sleeves was validated using two verification methods. First, the manufacturing process for rotary sleeves was simulated by FEM. After that, the process was modeled physically in laboratory conditions using 1:2 scale tools and a material model of aluminum alloy EN AW-6060. The results of the study lead to the following conclusions:

  1. 1.

    The numerical and experimental results confirm that rotary sleeves can be produced by extrusion and forging operations.

  2. 2.

    The numerical and experimental outside dimensions of forgings are similar. Relative error for seven dimensions is below 2.4%, in the case of one dimension is 18.75%.

  3. 3.

    The numerically and experimentally predicted location and size of the region in which the material is not in contact with the pin are not similar. This may result from the fact that the phenomenon of air cushion formation was not taken into consideration in the FEM simulation.

  4. 4.

    The material data of EN 42CrMo4 steel (elongation A), the distribution of the Cockcroft-Latham criterion and the critical value of the Cockcroft-Latham demonstrated that the forging process should be free from material cracking.

  5. 5.

    Distribution of forging forces estimated with both methods is very similar. Determination coefficients for the first, second and third forging operation are, respectively: 0.85, 0.94, 0.90. Only in the case of extrusion differences at the initial stage of the process occur, which is why the determination coefficient is the smallest and reached 0.72.

  6. 6.

    Maximum values of forces in the case of extrusion and forging 3 are compliant with the difference being only 0.7%. In the case of forging 1 and 2 the discrepancies are greater, respectively, 18 and 11% and may result from imprecise stopping of the machine, which in the case of forging may hugely influence the value of maximum force.