Introduction

Nickel/aluminum reactive nanocomposites are of primary interest in joining applications. In reactive bonding, the reactive nanocomposite is placed in-between the bonding partners. Thanks to the rapid, self-propagating high-temperature synthesis (SHS) between Ni and Al, the heat delivered by the reaction is provided directly in the joining zone without any further supply of energy. Typically, the nanocomposite is combined with layers of solder that melt during this process. The ignition of the reaction takes place outside the joining zone at a discrete point, the components are heated only locally, and the dwell time of heating is considerably reduced, compared to those of conventional joining processes. Use of this SHS-based joining technique could limit structural changes or residual stresses in the components observed in conventional joining technologies.

The most widespread Ni/Al nanocomposites are the reactive multilayer nanofoils (RMNF) produced by magnetron sputtering on a substrate or as free-standing foils (commercially available—Nanofoils®). Reactive multilayer nanofoils contain hundreds of alternating Ni and Al layers, with bilayer thicknesses ranging from a few to a hundred nanometers (Ref 1).

Nickel/aluminum RMNFs are widely used to bond metals or lightweight alloys (TiAl, Inconel) (Ref 2,3,4), carbon materials (Ref 5), ceramic-metal pairs (Ref 6), metallic glasses (Ref 7) and heat-sensitive materials (Ref 8, 9).

In order to bypass the limitations of the magnetron sputtering technique, including low productivity and high cost, different methods based on mechanical treatment have been developed, such as multiple cold rolling (Ref 10) or high energy ball milling combined with cold rolling (Ref 11) that lead to a complex assembly of grains with discontinuous layers. The self-propagating high-temperature reaction (SHS) was studied in compacted samples of Ni/Al mechanically activated powders (Ref 12, 13). Instead of multilayer systems, Nickel/Aluminum nanocomposites were used to join heterogeneous materials in micro-electromechanical systems (Ref 14). The nanolaminated structure of particles was found to play a crucial role in the reactivity of Ni/Al composites.

Modeling of the reactivity of Ni/Al RMNFs by means of molecular dynamics simulations is an active area of research (Ref 15). The exothermic dissolution of Ni in Al liquid at interfaces (Ref 16), the characteristics of the reactive front propagation (Ref 17, 18) and the influence of initial conditions on final microstructure (Ref 19) have all been considered and compared to experimental observations. But the modeling of reactive nanocomposites produced by high energy ball milling and cold rolled remains to be carried out. In this work, we present a first attempt to handle such systems. The model captures the main aspects associated with this specific microstructure: Particles with a nanolaminated structure are pressed to form a free-standing foil that can be used in joining applications. The very possibility of propagation as well as front characteristics will be compared to a standard Ni/Al RMNF. Features of the local dynamics such as NiAl formation will be analyzed. The system is hereafter referred to as ‘mechanically activated reactive multilayer nanofoils’ (MA-RMNF).

Simulation Details

Since 2015, we have been engaged in the ongoing development of an original method simulating self-propagating reactions by means of molecular dynamics simulations (MD). In this paper, which focuses on complex Ni/Al nanofoils, we give only the broad outline of the simulation procedure and advise readers to refer to our previously published papers for specific details (Ref 17, 19, 20). Simulations were performed using LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) (Ref 21) and the embedded atom method (EAM) potential fitted for Ni-Al by Purja Pun and Mishin (Ref 22). Equations of motion were integrated with a time step dt = 2 fs. Canonical (NVT) and isothermal-isobaric (NPT) runs employed a Nose–Hoover thermostat and barostat with temperature and pressure damping parameters equal to 0.2 and 2.0 ps. Periodic boundary conditions were applied along y and z while the x-direction was shrink wrapped.

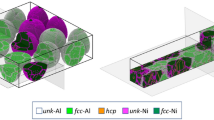
We considered an elongated simulation box of 580.61 × 57.30 × 1.43 nm. As shown in Fig. 1(a), the pore-free system contains 160 randomly distributed/oriented grains with a diameter of 15 nm for a total of 3,445,821 atoms (1,780,323 Ni and 1,665,498 Al). The polycrystalline structure was created by Voronoï tessellation and filled with <001> oriented columnar grains, randomly rotated around the z-direction (Ref 23). The bilayer thickness (\(H\)) is equal to 7.5 nm. The entire system was relaxed to reach thermal equilibrium with an NPT run at 300 K. The ignition was produced by local heating, at 1200 K, of the left extremity of the sample over 80 ps. In that region (i.e.,\(x<50\) nm), atoms evolved in the NVT ensemble, while other atoms were integrated into the NVE ensemble. The adiabatic conditions allowed us to simulate the exothermic character of the system, a key aspect in the SHS process both regarding exothermic dissolution and formation of intermetallic compound. After the ignition step, the thermostat was removed and the front dynamic proceeded in the microcanonical ensemble. This computational procedure mimics the experimental procedure in which local heating induces the start of the reaction wave.

Fig. 1
figure 1

(a) Schematic representation of the initial state of the system. (b) Histogram of average grain sizes. (c) Enlarged view of a lamellar grain

Full size image

The raw simulation data were analyzed using the open-source software OVITO (Ref 24), which provides visualization of the atomic trajectories as well as computation of the local atomic environment via an adaptive common neighbor analysis (a-CNA).

Results and Discussions

The first issue is the very possibility of SHS in such a system. After initiation at one edge of the sample, we observed a reactive front that propagated across the sample in a self-sustaining manner, without any further energy supply. The temperature profile is represented in Fig. 2 at different times. The melting temperature of aluminum delineated a zone mainly dominated by conduction (\({T}_{0}<T<{T}_{m}^{\text{Al}}\) ) and a reaction zone (\(T>{T}_{m}^{\text{Al}}\) ). The reaction zone is divided into a thin zone I: \({T}_{m}^{\text{Al}}<T<{T}_{c,1}\) and a broader zone II: \({T}_{c,1}<T<{T}_{c}\). Zone I corresponds to the exothermic dissolution of Ni into Al liquid, while zone II is associated with post-combustion processes. The front propagation is mainly driven by exothermic dissolution. The temperature in zone II continued to evolve after the passage of the front.

Fig. 2
figure 2

Temperature profiles. The horizontal lines indicate \({T}_{0}\), the initial temperature; \({T}_{m}^{\text{Al}}\), the melting temperature of A; \({T}_{c}\), the combustion temperature at 12 ns. The dot indicates \({T}^{*}\), the reference temperature corresponding to the instantaneous position of the front.

Full size image

In order to determine the propagation velocity, the position of the front corresponding to a given temperature (T*  = 1000 K) is determined as a function of time. The dependence was found to be linear, indicating a stationary combustion regime. The computed velocity is \(u \sim\) 17 m/s. The width of the conduction zone can be estimated as \(\Delta x =\upkappa / u\), where the thermal diffusivity \(\upkappa =4.71{ 10}^{-6}\) m2/s is evaluated at 300 K (Ref 20). For the measured velocity, the preheated zone, \(\Delta x = 277\) nm, remains smaller than the total length of the system.

Figure 3 shows snapshots of the system at different times. The reactive front propagates in the unreacted region (on the right) across the foil. A thin active zone, around the Al melting point, is associated with the progressive dissolution of Ni into Al liquid. In the post-combustion region (on the left), liquid solution Al + Ni coexists with B2-NiAl grains. Further from the dissolution region, the B2-NiAl grains are larger.

Fig. 3
figure 3

Snapshots of the system at different times (\(x < 200\) nm)

Full size image

In the MA-RMNF considered in this study, individual particles have an average diameter of 15.5 nm (see Fig. 1b) and each particle contains two bilayers of 7.5 nm. Figure 1(c) shows a typical grain with two bilayers, after relaxation at 300 K. We noted three types of grain boundaries: internal GB at interfaces between Al and Ni mainly composed of unk-Al; internal GB in Al layers; and external GB around the grain. Because aluminum is more ductile than nickel, aluminum accommodated the lattice mismatch and defects are formed inside Al layers. External GBs contain both unk-Al and unk-Ni. Table 1 presents the comparison between front characteristics of the MA-RMNF and RMNFs of similar bilayer thickness. RMNFs contain alternating Ni and Al layers, of constant thickness, across the foil. In MA-RMNF, layers are disrupted across the foil. The nano-layering is more complex in MA-RMNF. We noted that the front velocity and combustion temperature are higher in MA-RMNF in comparison with RMNFs. A careful study of the local dynamics could explain this extreme MA-RMNF reactivity.

Table 1 Front characteristics
Full size table

A representative slice around \(x = 150\) nm was used to analyze local dynamics. Figure 4 shows the evolution of local quantities and temperature, T. The local structure can be depicted by a-CNA in terms of the atomic percentage of atoms in their local environment (fcc, bcc or unknown). If the crystallographic environment of an atom is not well established, the analysis lists the atom as ‘unknown atom.’ In this case, the atom either belongs to an amorphous solid phase or a liquid phase. Representative snapshots, at different times, are given in Fig. 5. The snapshot of the system after thermalization at 300K, at \(t=0.4\) ns, (Fig. 5a) shows lamellar hexagonal grains separated by grain boundaries (GB). These GB are composed of unk-atoms with a majority of Al atoms. In addition, inner layers of aluminum contain both fcc- and unk-atoms. Initially, the ratio fcc/unk is approximately 1.5 (i.e., 30/20) for Al and 9 (i.e., 45/5) for Ni. The excess of unk-Al directly reflects the presence of lattice defects due to the ductility of Al which deforms more readily than Ni to fit the geometry imposed by the simulation box.

Fig. 4
figure 4

Temperature profile and structure analysis in a slice of 40 nm, around \(x=150\) nm

Full size image
Fig. 5
figure 5

Snapshots of the slice of Fig. 4 (slice of 40 nm, around \(x=150\) nm)

Full size image

Five stages are identified in Fig. 4:

  1. I.

    The temperature increased slightly because of heating by conduction. A slight increase in fcc-Al was observed corresponding to grain coarsening or annihilation of defects within the layers of Al.

  2. II.

    The number of fcc-atoms started to decrease with increasing unk-atoms. Amorphization of Al took place prior to its melting point with an increase from 20 to 25 at.%. Figure 5(b), at \(t=5\) ns, shows incoming Ni-atoms at grain boundaries.

  3. III.

    Between \(t=5\) and \(t=7.5\) ns, the evolution is drastic. The fraction of unk-Al increased as all fcc-Al became amorphous. At the end, there were no more fcc-Al atoms. The number of unk-Ni sharply increased because of the dissolution of Ni atoms in the amorphous phase. The exothermic character of dissolution induced an increase in temperature until the melting point of Al (\({T}_{m}^{\text{Al}}=1055\) K (Ref 20)) was reached. Figure 5(c), (d), (e) and (f) illustrates the associated microscopic processes:

    • At \(t=6\) ns, three small slices coexist: unreacted fcc-Al and fcc-Ni (on the right), unk-Al and fcc-Ni (in the middle) and a liquid solution of Ni and Al (on the left). The layers of Ni progressively shrank and became thinner. Some isolated “Ni-fingers” were embedded in the liquid and surrounded by an excess of unk-Ni. There is a time lapse between the amorphization of Al and Ni, associated with the progressive dissolution of Ni. This time interval corresponds to the occurrence of the first exothermic reaction.

    • At \(t=7\) ns, the dissolution front has moved forward to the left. Small Ni-fingers have disappeared, while seeds of the intermetallic B2-NiAl have formed, hanging on at the edge of the fingers.

    • Between \(t=7.25\) and \(t=7.5\) ns, the seeds grew into B2-NiAl grains and detached from the Ni-fingers.

  4. IV.

    The fraction of unk-Al has decreased while the fraction of unk-Ni continues to increase. The fraction of bcc-atoms has started to increase, together with temperature. At \(t=8\) ns (Fig. 5g), the slice is filled by a liquid solution Ni + Al, grains of B2-NiAl and unreacted Ni-fingers. At the end stage IV, the fraction of unk-Ni has reached a maximum. There are no longer any fcc-Ni atoms.

  5. V.

    During stage V, the number of bcc-atoms mirrored the variation in unk-atoms. As shown in Fig. 5(h), B2-NiAl grains continued to grow while new grains appeared and others partly dissolved. During stages IV and V, the temperature continued to increase but remained below the melting temperature of the intermetallic compound (\({T}_{m}^{\text{NiAl}}=1850\) K (Ref 20)). The second exothermic reaction takes place at this time.

After the passage of the dissolution front, the post-combustion region filled with a liquid solution of Ni and Al. The mixing between Al and Ni was very efficient at the scale of the nano-heterogeneity, resulting in a uniform equimolar solution. In addition, the combustion temperature remained lower than the melting temperature of the B2-NiAl intermetallic compound. Conditions such as perfect mixing and undercooling are suitable for the nucleation of B2-NiAl. As shown in Fig. 5(d), B2-NiAl nuclei indeed appeared at the ends of the Ni-fingers. Once formed, grains detached from their support due to the fast propagation of the dissolution front (Fig. 5e and f). The small grains embedded in the Ni-Al liquid solution grew (Fig. 5g and h).

The grain dynamics are depicted in Fig. 6, where the evolution in the number of B2-NiAl grains and size of the largest grain is depicted. A sustained nucleation of B2-NiAl grains was observed. Up to 7 ns, the number of grains increased; after 7 ns, a plateau was reached. This corresponds to a nucleation-dissolution process with formation of nuclei, dissolution of smaller grains and growth of larger ones.

Fig. 6
figure 6

Number of B2-NiAl grains and size (number of atoms) of the largest grain as a function of time

Full size image

Next, we considered two representative grains, G1 and G2, between 4 and 6 ns (see Fig. 3 and 7a). Figure 7(d) depicts the size of the two grains as a function of time. After nucleation, grain G1 grew rapidly and continuously. Growth of G1 is associated both with precipitation (from the liquid solution) and coalescence with neighboring grains. Grain G2 grew more slowly and reached a maximum of 4228 atoms (volume of 58 nm3 corresponding to a sphere of 3.7 nm). After \(t=5\) ns, its size started to decrease, and after \(6\) ns, the grain disappeared. In a previous work (Ref 25), we observed Oswald ripening of NiAl grains in non-stoichiometric RMNFs. Behind the front, a concentration gradient between the melt and the NiAl particles was clearly demonstrated. This is not the case in the present study where both the liquid mixture and the growing particles are stoichiometric. As shown in Fig. 7(b), the local concentration in Ni is uniform around the B2-NiAl grains.

Fig. 7
figure 7

(a) Snapshot of a slice of \(30\) nm around \(x = 80\) nm, at \(t = 5\) ns. (b) Local concentration in Ni in the liquid solution. B2-NiAl grains are colored in blue. (c) Texture of the B2-NiAl grains. Color bar corresponds to the local orientation of the bcc-atom with its six nearest neighbors, belonging to crystallized grains. See (Ref 25) for more details. (d) Evolution of the size (number of atoms) of two selected grains: G1 and G2. (e) Local temperature around \(x = 80\) nm, estimated melting temperature of grains G1 and G2 as a function of time

Full size image

The disappearance of small grains is due to their dissolution into the liquid. The melting temperature of nanometric grains is actually different from the melting temperature of bulk material. By means of MD simulations, the melting temperature of NiAl spherical nanoparticles can be evaluated as a function of their size (Ref 20). We did not consider free-standing nanoparticles here, as is the usual practice, but rather B2-NiAl spheres embedded into an overcooled stoichiometric liquid solution of Ni and Al. The relation between the melting temperature and the number of atoms in the particle adheres to the well-known Gibbs–Thompson equation:

$${T}_{m}\left(N\right)={T}_{m,\mathrm{bulk}}-k{N}^{-1/3}$$

where Tm,bulk = 1895 K is the estimated melting temperature of the bulk, obtained by means of the embedded-sphere simulation, and \(k=5250 {K}\). Given their number of atoms, the melting temperatures of grains G1 and G2 were estimated and plotted in Fig. 7(e) along with the local temperature, \({T}_{\mathrm{loc}},\) in the region surrounding the two grains. Between 4 and 6 ns, \({T}_{\mathrm{loc}}\) increases from 1600 to 1800 K due to NiAl formation. Since \({T}_{m}\left(G1\right)\) remains higher than \({T}_{\mathrm{loc}}\), the growth of G1 is not affected. After nucleation and detachment from the solid Ni-finger, G2 grows until \({T}_{loc}\) exceeds \({T}_{m}\left(G2\right)\), at 5.3 ns. Then, grain G2 begins to melt. The variation in \({T}_{\mathrm{loc}}\) is thus sufficient to induce the melting of small B2-NiAl grains into liquid solution.

On the other hand, small grains are often characterized by slightly different crystallographic orientations within a single grain that could affect their stability. As shown in Fig. 7(b), we calculated the texture of B2-NiAl grains in a slice along the \(x\)-direction (\(65 < x < 95\) nm) at \(t = 5\) ns, following the method developed in (Ref 25). The large grain G1 has a specific orientation while grain G2 contains atoms with two slightly different orientations.

Conclusions

MA-RMNFs represent an interesting alternative to usual RMNFs for purposes of reactive joining thanks to their low cost and easy fabrication. The main features of their reactive behavior are summarized here:

  • The reaction can be started in systems at room temperature (300 K) and is self-propagating.

  • Amorphization of Al-atoms occurs below the melting point of aluminum.

  • Front velocity and combustion temperature are higher than the corresponding values in RMNFS.

  • A two-step exothermic reaction occurs: exothermic dissolution of Ni in an amorphous phase and the formation of intermetallic compound B2-NiAl. The second step takes place in the post-combustion zone.

  • After heterogeneous nucleation on solid Ni-fingers, B2-NiAl formation follows a precipitation-dissolution mechanism.