Problem of Identification of Phase Transformation Models Used in Simulations of Steels Processing

Abstract

Accuracy of phase transformation models depends on the correctness of coefficients evaluation, adequate to the investigated material. Dilatometric tests combined with the inverse analysis are used to perform identification. Since the problem is nonlinear, analytical approach is not possible and the inverse solution is transferred into the optimization task. It leads to difficulties typical for optimization of multivariable function such as local minima and lack of proof of the uniqueness. The problem of the effectiveness and uniqueness of the inverse algorithms used for identification of phase transformation models for steels was investigated for two models. The first was a modified JMAK (Johnson–Mehl–Avrami–Kolmogorov) equation. The second was an upgrade of the Leblond equation, in which second-order derivative of the volume fraction with respect to time was introduced. In classical identification, the result for one transformation depends on the coefficients for the remaining transformations and optimization has to be performed several times until the compatibility between transformations is reached. To avoid encountered problems, complex optimization simultaneously for all coefficients in the models was performed. This approach was based on nature-inspired optimization techniques. Models with identified coefficients for various steels were validated in simulations of industrial processes of laminar cooling and continuous annealing of strips.

Introduction

Computer-aided design of materials processing is common now. Beyond one-step processes, whole manufacturing chains are simulated. Typical optimization problems for manufacturing chains are based on simulations of various variants of several processes according to the applied optimization technique. Fully coupled thermal–mechanical–microstructural models are needed to perform simulations and calculate the objective function.

Microstructural part of the models is composed of microstructure evolution during hot forming and phase transformations during cooling. The latter describes kinetics of phase transformation, and it was considered in the present work. A variety of phase transformation models of various complexities were developed; see the book (Ref 1). Accuracy of predictions of these models depends, to a large extent, on the correctness of evaluation of materials coefficients in the models. Equilibrium phase compositions and concentrations of elements are well described by the thermodynamic equations. In the present paper, these parameters were determined using ThermoCalc software and they were used as boundary conditions for the transient models. Coefficients in the models of kinetics are usually determined on the basis of dilatometric tests performed at various cooling rates. Since transformations influence each other, an application of typical curve fitting methods presents difficulties and an inverse approach is applied. Phase transformation equations are nonlinear, and analytical finding of the inverse operator is not possible; therefore, the problem is transformed into the optimization task. Regarding phase transformations, direct measurements of the sample elongation can be used as an input for the inverse analysis. Beyond this, although dilatometric samples are usually very small, some heterogeneity of temperature may still exist. Therefore, finite element (FE) simulation of the temperature distribution is added and calculated temperature can be compared with the measurements using thermocouple welded to the side of the sample. This approach was used in publication (Ref 2). The same approach with thorough description of the mathematical formalism can be found in the PhD thesis (Ref 3). Various parts of this approach are described in earlier publications (Ref 4, 5). Other, mathematically advance solutions for phase transformations include derivation of equations that relate parameters of the continuum method to the measurable quantities like interface energy and kinetic coefficient (Ref 6), as well as identification of phase field model (Ref 7). All these approaches lead to computationally complex and costly tasks. Authors research have been for some time focused on selection of the best model by searching for a balance between predictive capabilities of various materials processing models and computing costs (Ref 1), and observations from these research were applied in the present work.

The inverse algorithm proposed by the authors is described in Ref 8, and application to the phase transformation models is presented in Ref 1, 9, including mathematical background and usage of the sensitivity analysis. This approach leads to difficulties typical for optimization of multivariable function such as local minima and lack of proof of the uniqueness of the solution. Investigation of these problems, as well as a selection of the best optimization method for the inverse algorithm, was the main objective of the present work. Following numerous publications (e.g., Ref 10, 11), the nature-inspired methods were primarily considered in Ref 12 with the focus on genetic algorithms (GA) and particle swarm optimization (PSO). Review of the applications (Ref 13) of these methods in materials science can be found in Ref 14. The present work is an extension of Ref 12 with a particular emphasis on evaluation of the algorithms, analysis of the computing costs and practical application to the industrial processes.

Due to mutual relation between transformations, in classical identification the result for one transformation depends on the coefficients for the remaining transformations and optimization has to be performed several times until the compatibility between transformations is reached. It is time-consuming and does not solve the problem with the uniqueness. To avoid encountered problems, complex optimization simultaneously for all coefficients in the models was performed. Solution of the optimization task is costly, and there is a continuous search for the most efficient method. Comparison of various optimization methods and selection of the best method was one of the objectives of the work.

Phase Transformation Models

A variety of phase transformation models of various complexities of mathematical description and of various predictive capabilities were investigated by the authors. An attempt of classification of these models in the coordinate system computing costs versus predictive capabilities was presented in Ref 15. Upgraded version of this classification is shown in Fig. 1. Since prospective applications of the models are connected with optimization of manufacturing chains, low computing times are of major importance. Therefore, two of these models with very short computing times were investigated in the present work. These are Johnson–Mehl–Avrami–Kolmogorov (JMAK) upgrade and second-order differential equation. Both models are described in earlier publications, and they are only briefly discussed in the present paper.

Fig. 1

Classification of phase transformation models with respect to their predictive capabilities and computing time

JMAK Model

JMAK basic equation describes the kinetics of phase transformation:

$$X = 1 - \exp \left( { - kt^{n} } \right)$$

(1)

where X—volume fractions of a new phase, t—time, k, n—coefficients.

The values of n are introduced in the model as a₄, a₁₅ and a₂₄ for ferrite, pearlite and bainite transformations, respectively. The coefficient k is defined as a function of the temperature. All equations of the model are given in Table 1 where T—temperature in °C, T_K—temperature in K, R—gas constant, F_f, F_p, F_b, F_m,—volume fractions of ferrite, pearlite, bainite and martensite, respectively, [C], [Mn], [Ni]—concentrations in wt.% of carbon, manganese and nickel, respectively. Pearlite transformation begins when carbon concentration in the austenite reaches that at the γ/cementite interface (c_γβ) in the considered temperature.

Table 1 Equations in the JMAK model

Numerical solution of this model is described in Ref 1. The model was implemented by the authors into the finite FE code and used for simulation and optimization of various industrial processes; see solutions for forging and cooling of heavy crankshafts (Ref 16) and for welding (Ref 17).

Model Based on the Control Theory

The idea of this model is based on the Leblond equation (Ref 18). The main assumption of Leblond was that the rate of the transformation is proportional to the distance from the equilibrium:

$$\frac{{{\text{d}}X}}{{{\text{d}}t}} = k\left( {X_{\text{eq}} - X} \right)$$

(2)

where X—volume fraction of a new phase, X_eq—equilibrium volume fractions of a new phase in the current temperature, k—coefficient.

In the present paper, the model was applied for the ferritic transformation only. Kinetics of ferritic transformation is characterized by two stages. The first stage is some delay due to time needed for nucleation of the new grains. The second stage is the maximum rate of the transformation due to growth of a new phase. Since Eq 2 describes the first-order inertia term, it is not capable of accounting for the delay of the response. Thus, the second-order equation was proposed in Ref 19 to eliminate this constraint:

$$B_{1}^{2} \frac{{{\text{d}}^{2} X}}{{{\text{d}}t^{2} }} + B_{2} \frac{{{\text{d}}X}}{{{\text{d}}t}} + X = f\left( T \right)$$

(3)

where B₁, B₂—time constants defined as functions of the temperature.

Right-hand side of Eq 3 is a function of temperature, as well. This function has to be equal to the equilibrium volume fraction of ferrite at the considered temperature:

$$f\left( T \right) = \frac{{F_{{{\text{f}}_{T} }} }}{{F_{{{\text{f}}_{\hbox{max} } }} }}$$

(4)

where

$$F_{{f_{\hbox{max} } }} = 1 - \frac{{\left( {c_{0} - c_{\alpha } } \right)}}{{\left( {c_{\text{eut}} - c_{\alpha } } \right)}}$$

(5)

$$F_{{{\text{f}}_{T} }} = \frac{{c_{\gamma \alpha } - c_{0} }}{{c_{\gamma \alpha } - c_{\alpha } }}$$

(6)

where c₀—carbon content in steel, c_α—carbon content in ferrite, c_eut—carbon content at eutectic, which is calculated as crossing point between lines c_γα and c_γβ determined from the ThermoCalc software. c_γα is the carbon concentration at the γ/α interface, and c_γβ is the carbon concentration at the γ/cementite interface.

Equation 3 is typical for the second-order inertia term in the control theory; therefore, this model will be referred to in the present paper as the CONT model. Volume fraction X in Eq 3 is calculated with respect to the maximum volume fraction $F_{{f_{\hbox{max} } }}$ in the steel defined by Eq 5. Time constants B₁ and B₂ in this equation are responsible for the delay of the response and for the rate of the response, respectively. Thus, when response of the material to the step function ΔT is considered, time constant B₁ determines the initial delay of this response. Therefore, B₁ was correlated with the rate of nucleation, which is directly connected with the undercooling below A_c3:

$$B_{1} = a_{4} \exp \left[ { - a_{5} \left( {A_{e3} - T} \right)} \right]$$

(7)

where a₄, a₅—coefficients.

Time constant B₂ is responsible for the growth of the ferrite phase, and it was correlated with the diffusion coefficient and the interface mobility. The assumption was made that B₂ is inversely proportional to the modified Gauss function with the nose located at the temperature of the maximum rate of the transformation (coefficient a₇ in the model):

$$B_{2} = \left\{ {a_{6} \exp \left[ { - \left( {\frac{{a_{7} - T}}{{a_{8} }}} \right)^{2} } \right]} \right\}^{ - 1}$$

(8)

where a₆, a₇, a₈—coefficients.

Modeling of the ferrite phase transformations begins with Eq 3 when the temperature drops below A_c3. As it has already been mentioned, the transformed ferrite volume fraction X is calculated with respect to the maximum volume fraction of this phase in steel $F_{{f_{\hbox{max} } }}$. The maximum value of X, which can be obtained, changes when temperature T is changing. This maximum value is determined by the line c_γα, and it is equal to the right-hand side of Eq 3.

More details about the CONT model can be found in Ref 19. In the present work, Eq 3 was solved using the implicit finite difference method. During continuous cooling, simulation lasts until the transformed volume fraction X achieves 1. However, when carbon content in the austenite exceeds the limiting value c_γβ, the austenite–pearlite transformation begins in the remaining volume of the austenite.

Inverse Approach

Both models contain coefficients, which are grouped in the vector a. These coefficients were identified using inverse analysis of the dilatometric tests. Flowchart of this algorithm is shown in Fig. 2. Results of dilatometric tests, including measurements of the start and end temperatures for transformation and volume fractions of phases after cooling, were used as an input to the inverse analysis. Thus, in the case of dilatometric tests, the objective function is defined as:

$$\Phi ({\mathbf{a}},{\mathbf{p}}) = \sqrt {\frac{{w_{\text{T}} }}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{T_{\text{im}} - T_{\text{ic}} }}{{T_{\text{im}} }}} \right)^{2} + \frac{{w_{\text{X}} }}{k}\sum\limits_{i = 1}^{k} {\left( {\frac{{X_{\text{im}} - X_{\text{ic}} }}{{X_{\text{im}} }}} \right)^{2} } } }$$

(9)

where T_im, T_ic—measured and calculated start and end temperatures of phase transformations, X_im, X_ic—measured and calculated volume fractions of phases after cooling, w_T, w_X—weights, n, k—number of measurements of temperatures and volume fractions of phases, respectively.

Fig. 2

Flowchart of the inverse algorithm used in the present work

In conventional approach, coefficients for each transformation were determined separately. Since, as it was mentioned in Introduction, a mutual relation between transformations exists, and the result for one transformation depends on the coefficients for the remaining transformations. The optimization had to be performed several times until the compatibility between various transformations was reached. Thus, the conventional inverse analysis requires a lot of manual corrections and calculations, which are caused by the following issues:

• strong interrelations between models simulating different phase transformations,

• multidimensional character of models on input and output,

• huge number of local minima, an example of which is shown in Ref 12 for the ferrite start temperature.

It was concluded that it is almost impossible to apply conventional optimization methods automatically. Manual actions during calculations take a lot of time and require numerical experience, as well as deep knowledge of the phase transformation. All these facts cause that classical optimization is time-consuming, accuracy is low and problems with the uniqueness are not solve. On the other hand, precision of the identification highly influences modeling reliability. This is visible especially in application to the modern multiphase advanced high-strength steels (AHSS), in which high properties are obtained by composition of soft ferrite with hard constituents at specifically prescribed proportions. Manufacturing of these steels requires complex thermal cycles, which allow to obtain required specific phase composition. Two problems are essential (Ref 12): (i) efficiency of the inverse algorithms used for identification of phase transformation models and (ii) final reliability of the identified models in numerical simulations of manufacturing processes. To avoid encountered problems, complex optimization simultaneously for all coefficients in the models was performed in the present work. Computer science aspects of this approach were investigated in Ref 12. The identification was performed by coupling the selected model with various nature-inspired optimization techniques and performing inverse analysis for the experimental data. Two nature-inspired optimization methods, i.e., genetic algorithms (GA) and particle swarm optimization (PSO), were tested and compared. On the basis of literature review (Ref 10, 11, 20) and numerous tests, the particle swarm optimization (PSO) technique was selected in Ref 12 and it was used in the present work.

Similar problems occur when models with identified parameters are applied to simulation of industrial forming processes. Optimal technological parameters are also determined by solution of the inverse problem, which is often called reconstruction problem. Since global process parameters are determined by macroscale model, usually it is finite element (FE) method, and multiscale solution is needed to predict kinetics of phase transformation. Brief discussion of the computing costs connected with multiscale modeling is presented in the next chapter.

Computing Costs in Multiscale Modeling of Materials Processing

Problems of computing costs in modeling of materials processing have been in the field of interest for scientists for a few decades now. It is due mainly to the fact that simulations of processing of materials usually require multiscale models, which describe multiphysical phenomena (Ref 1). As it is shown in Ref 21, accounting for various dimensional scales may have significantly different influences on computing costs, depending on the type of the connection between the scales, which is schematically shown in Fig. 3. Feedback from the microscale to the macroscale is the main factor influencing the computing costs.

Fig. 3

Schematic illustration of the computing costs of multiscale models depending on the connection between scales (Ref 23)

Uncoupled solutions, which do not need feedback from micro- to macroscales, do not require long computing times. Microscale calculations can be usually performed as postprocessing, which fosters application of the distributed computing methods. Thus, application of discrete microscale models [CA—cellular automata, DIFF—model based on the solution of the diffusion equation (Ref 22)] does not lead to very long computing times. Contrary, when feedback from micro- to macroscale is needed (coupled solutions), microscale calculations have to be performed online at each Gauss point of the macroscale. It leads to very long computing times. Increase in the computing times in fully coupled solutions depends on whether only thermal or also mechanical feedback is needed. In the former case, an increase in the computing time is acceptable and application of the discrete models in the microscale (CA, DIFF) leads to long but still reasonable computing times. In the case of mechanical feedback (e.g., dilatometric strains), the computing times raise to not acceptable level and only very simple microscale models can be used.

The objective of the present work was identification of models which can be efficiently used for optimization of complex industrial processes. Therefore, JMAK and CONT models, which almost do not affect the time of multiscale calculations (Fig. 3), were selected.

Experiment and Identification

Experiment

Three materials were selected for the analysis. All materials were steels, which belong to the AHSS group. Chemical composition of these steels is given in Table 2. Steels A and B are typical dual phase (DP) steels with different carbon contents. Steel C is a bainitic steel with increased content of the silicon. The dilatometric tests were performed for a wide range of cooling rates. Before cooling, the samples were subjected to different thermomechanical treatments. All the samples from the steels A and B were subjected to austenitization at 1050 °C for 300 s followed by deformation above the recrystallization temperature. The first set of the samples from the steel C was subjected to austenitization at 1100 °C for 300 s followed by deformation above recrystallization temperature. These steels are referred to as steel CRX. Additionally, some samples of the steel C after austenitization were cooled to 850 °C and deformation was performed below the recrystallization temperature. These samples are referred to as steel CNR.

Table 2 Chemical composition of the investigated steels, wt.%

PSO method (see section 2.3) was used for the model identification. Coefficients determined for both models are given in Table 3 for the JMAK model and in Table 4 for the CONT model (ferrite transformation only). Both models were verified by comparison of the predictions with measurements for the transformations start and end temperatures; see selected results for JMAK model only in Fig. 4, and good agreement was obtained for all models. Comparison with earlier works, in which simplex optimization method was used (Ref 19, 23), showed that PSO allowed to obtain much lower value of the objective function 9. It means that global optimum was reached and much better accuracy of the model was obtained. Due to this, the models could be further used for the precise analysis of the influence of carbon concentration in steels A and B and for the influence of thermomechanical treatment parameters in steel C.

Table 3 Coefficients in the JMAK phase transformation model for the investigated steels, wt.%

Table 4 Coefficients in the CONT phase transformation model for the investigated steels, wt.%

Fig. 4

Kinetics of transformations for the optimal laminar cooling schedules for the steels A (a) and C (b)

Analysis of the computational complexity showed that it is similar for both models and they can be used alternatively. All the results presented in the following parts of this paper were obtained for the JMAK model.

All samples after dilatometric tests were subjected to microstructure analysis using light optical microscope (LOM) and scanning electron microscope (SEM). Selected micrographs for the steel C are shown in Fig. 5 for the LOM and in Fig. 6 for the SEM. Analysis of the micrographs shows that the microstructure of the sample subject to phase transformations in the as-recrystallized state is composed of allotrimorphic ferrite and martensite/bainite islands. On the contrary, the microstructure obtained from the non-recrystallized austenite is more uniform and is composed of allotrimorphic ferrite, granular bainite and martensite.

Fig. 5

Selected LOM micrographs for the steel C in recrystallized (a, c) and non-recrystallized (b, d) condition cooled with the rate of 1 °C/s (a, b) and 84 °C/s (b, d)

Fig. 6

Selected SEM micrographs for the steel C in recrystallized (a, c) and non-recrystallized (b, d) condition cooled with the rate of 1 °C/s (a, b) and 84 °C/s (c, d)

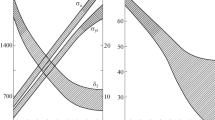
Very good results of identification of the models allowed to use these models for comparison of phase transformations kinetics in the investigated steels. Calculated CTT graphs for the steels A and B are shown in Fig. 7(a). Higher carbon content in the steel B causes a decrease in the B_s and M_s temperatures and an increase in the range of the pearlite transformation. Slight effect on the ferrite start transformation was observed, as well.

Fig. 7

Comparison of the CCT diagrams for steels A and B (a) and for steel C in recrystallized and non-recrystallized condition (b)

Calculated CTT graphs for the steels C are shown in Fig. 7(b). Analysis of the plots in this figure shows that deformation of the austenite accelerates ferrite transformation and lowers B_s temperature. The latter is observed only for larger cooling rates. No effect of the austenite deformation on the M_s temperature was observed.

Case Studies

Multiphase microstructure characteristic for the AHSSs can be obtained either during laminar cooling after hot rolling of strips or during intercritical annealing after cold rolling. Both processes, in which phase transformations are used to control properties of steel products, were considered as case studies in the present work. Optimization of these processes was performed with the required phase composition being the objective function. The phase transformation models described in the previous section were used. Since after using advanced identification method very good accuracy of the models was obtained (Fig. 8), similarly good reliability of the optimization can be expected.

Fig. 8

Measured (full symbols) and calculated (open symbols) start and end temperatures of transformations

Laminar Cooling

Laminar cooling is performed after hot rolling for strips with the thickness of few millimeters. Therefore, through thickness temperature variations are of importance and FE calculations of temperature in the macroscale had to be performed. Authors FE code described in Ref 24 was used for this purpose. Typical laminar cooling system composed of two sections is presented schematically in Fig. 9; see Ref 21 for more details. Notation in Fig. 9: T_f—finishing rolling temperature, $T_{{{\text{f}}_{\hbox{max} } }}$—temperature of the maximum rate of the ferrite transformation, T_c—coiling temperature, d—distance between the sections of the laminar cooling (20 m in the present work), v₆—exit velocity from the last stand, t_p—time between the two sections of the laminar cooling. A number of boxes in each zone of the laminar cooling is given in Fig. 9. Each box is 1 m long which gives the length of each section equal to 40 m. Numbers of boxes and maximum water flux (W) in the subsequent zones of the laminar cooling system are given in Table 5. Parameters of the laminar cooling were taken from one of the existing modern hot strip mills.

Fig. 9

Schematic illustration of a typical laminar cooling system

Table 5 Number of boxes and maximum water flux in the subsequent zones of the laminar cooling system (I—intensive zone, N—normal zone, T—trimming zone)

Microstructure of the DP steel is obtained by control of the ferritic transformation. Accelerated cooling is applied to the temperature of the lowest stability of austenite (about 670-720 °C). Slow cooling proceeds between the two sections of the cooling system until the required volume fraction of ferrite is obtained. Once this is achieved, fast cooling is applied to transform the remaining austenite to martensite. Practical realization of this scheme in the laminar cooling is difficult. Cooling rates depend on the thickness of the strip after the last stand (h₆) and on the strip velocity (v₆) which complicates selection of water fluxes in subsequent zones of the laminar cooling. Therefore, application of numerical modeling to design the laminar cooling schedule for DP steels is a part of the design of the manufacturing chain for these steels. In the present paper, the technology design for laminar cooling was formulated as an inverse problem of reconstruction. Required phase composition was the known output from the model. The best process parameters giving this phase composition were determined using optimization methods. The optimization task for the laminar cooling was formulated in Ref 23, and it is also discussed in the book publication (Ref 1). The objective function was to obtain F_f0 of ferrite and as low as possible amount of bainite:

$$\Phi = \sqrt {w_{\text{f}} \left( {F_{\text{f}} - F_{{{\text{f}}0}} } \right)^{2} + w_{\text{b}} F_{\text{b}} }$$

(10)

where F_f, F_b—volume fractions of ferrite and bainite, respectively, w_f, w_b—weights.

Water fluxes in subsequent zones of the laminar cooling were the design variables. Optimization was performed for the strip velocity 8 m/s and strip thickness 4 mm. The objective of the optimization was to obtain 80% of the ferrite and no bainite in the microstructure. Optimal laminar cooling parameters for the DP steels A and B are given in Table 6. Maximum water flux in the second section had to be applied to reach the required level of the martensite. Changes of the temperature and kinetics of transformation for the optimal cycle for the steel A are shown in Fig. 4. It is seen that exactly 80% of ferrite was obtained and that the volume fraction of bainite was below 3%. Optimization for the steel B yielded the same cooling parameters. However, the optimal microstructure contained 80% of the ferrite, 20% of the martensite and no bainite.

Table 6 Optimal water flux [m³/h] in the subsequent zones of the laminar cooling system for the strip velocity 8 m/s and the strip thickness 4 mm

Similar optimization was performed for the steel C, but the objective was to obtain purely bainitic microstructure. Optimal laminar cooling parameters for this steel are given in Table 6. Maximum water flux in the first two zones had to be applied to avoid ferrite. Changes of the temperature and kinetics of transformation for the optimal cycle for the steel C are shown in Fig. 4. Since bainitic transformation takes place in the coil, timescale in Fig. 4 changes at the beginning of coiling. It is seen that purely bainitic microstructure was obtained and that the volume fraction of ferrite was below 2%. Optimization for the steel CNR showed that due to faster ferrite transformation in the deformed austenite, more intensive cooling had to be applied to obtain purely bainitic microstructure. In consequence, bainitic transformation was faster (Fig. 4).

Intercritical Continuous Annealing

Typical continuous annealing thermal cycles to obtain DP (dual phase) or CP (complex phase) microstructures are discussed in Ref 25, 26. Schematic illustration of the thermal cycle for intercritical annealing and for full austenitization annealing is shown in Fig. 10. The strip is heated either to the intercritical temperature or above A_c3, maintained at this temperature and cooled. In the former case, two types of the ferrite are obtained in the microstructure. The first is recrystallized ferrite, which was not transformed into austenite during the cycle. The second is ferrite transformed from the austenite during cooling.

Fig. 10

Schematic illustration of the thermal cycle for intercritical annealing (solid line) and for full austenitization annealing (dashed line)

Continuous annealing is applied to thin strips (below 1 mm) after cold rolling, in which through thickness temperature variations are negligible. Beyond this, the strip temperature is controlled by the continuous annealing equipment. Therefore, macroscale calculations are not needed and optimization of the process can be effectively performed using advanced microscale models. The objective function for the intercritical annealing was to obtain F_f0 of ferrite, F_fRX0 of recrystallized ferrite and as low as possible amount of bainite:

$$\Phi = \sqrt {w_{\text{f}} \left( {F_{\text{f}} - F_{{{\text{f}}0}} } \right)^{2} + w_{{{\text{f}}RX}} \left( {F_{{{\text{f}}RX}} - F_{{{\text{f}}RX0}} } \right)^{2} + w_{b} F_{b} }$$

(11)

where F_f, F_fRX, F_b—volume fractions of ferrite, recrystallized ferrite and bainite, respectively, w_f, w_fRX, w_b—weights.

State variables vector composed parameters of the thermal cycle in Fig. 10. Heating rates t_h1 = 3 °C/s and t_h2 = 0.25 °C/s were assumed in the first approach; therefore, the following state variables remained: time of heating (t_h1) which determines the intercritical annealing temperature, time of at intercritical temperature (t_h2), time (t_c1) and cooling rate (C_r1) in the first step of cooling, time (t_c2) and cooling rate (C_r2) in the second step of cooling, cooling rate (C_r3) in the third step of cooling.

In the case of DP steels, the objective was to obtain 80% of ferrite including 50% of recrystallized ferrite (F_f0 = 0.8; F_fRX0 = 0.5). Optimal thermal cycles obtained for the steels A and B are shown in Fig. 11. Kinetics of phase transformation during heating and cooling stages is shown in this figure, as well.

Fig. 11

Optimal intercritical annealing cycles obtained for the steels A and B

Conclusions

The new approach based on the nature-inspired optimization algorithms to identification of the phase transformation models was proposed. Two single-point models were considered, modified JMAK and upgrade of the Leblond model. The models were identified for the two DP steels with different carbon contents and for the bainitic steel subjected to different thermomechanical treatments prior to cooling. The following conclusions were drawn:

• Simultaneous optimization for all transformations using PSO method gave much better result comparing to earlier solutions using non-gradient methods. The local minima were avoided, and the final value of the objective function (Eq 9), which is the measure of the accuracy, was much lower.

• The proposed approach was equipped with mechanism of dynamic extension of the searching space dimensions. It allowed to search the optimum in much wider space starting from smaller area created on the basis of current experience with different steels. This gave the possibility to minimize the number of the objective function evaluations at the beginning and to decrease the computing costs.

• Nature-inspired methods are capable of coping with the multimodal objective functions. This enables to investigate more than one local minima being close to each other, which was the case in the identification of the phase transformation models solved in this paper.

• Effective identification made the models sensitive to changes of the process parameters, and evaluation of the influence of carbon content in the DP steels and austenite deformation in the bainitic steels on the phase transformation kinetics was possible.

• Accurate identification of the models allowed better prediction of the material behavior during laminar cooling and continuous annealing processes. The identified models gave higher robustness of material behavior prediction in comparison with earlier approaches based on the conventional identification methods.