Introduction

Residual stresses can be a very dangerous feature when it comes to reduction in load-carrying capacity and strength in general. Such stresses can of course be introduced through mechanical and/or thermal loading but also during engineering, processing and production of monolithic and composite materials. Naturally, the best way to avoid any destructive influence from residual stresses is to substantially reduce the levels of the residual fields. However, very often this is not an easy task to undertake, and then, a more realistic approach to the problem is to quantify these stresses and account for them during design and dimensioning. There are numerous methods that have been suggested for this purpose (hole-drilling, layer removal, beam bending, neutron and x-ray tilt techniques just to mention a few), but lately indentation testing has emerged as an easy and nondestructive alternative. Accordingly, residual stress determination using indentation has developed into a very active research field during the last decades.

Arguably, this research started in a systematic manner when Tsui et al. (Ref 1) and Bolshakov et al. (Ref 2) investigated, some twenty years ago, experimentally and numerically the influence of residual stress on indentation properties at indentation of aluminum alloy 8009, by experimental and numerical (finite element) methods. In short, fundamental results were presented, showing that indentation hardness, in this paper defined as the average contact pressure, was invariant of such stresses while the amount of piling-up of material at the contact contour showed clear stress dependence. In short, piling-up increased at compression and decreased at tension. Further pertinent investigations include (Ref 3-12) (just to mention a few) introducing more theoretical approaches to the analysis of the mechanics of the problem. In most of these studies, progress was made based on the fact that hardness was not affected by residual stresses and the deformation at the contact contour could then be directly correlated with the magnitude of the residual (or applied stresses) present in the indented material.

Even though the invariance of indentation hardness obviously is a fundamental part, in an analysis of residual stress effects at indentation, the accuracy of this feature has not been investigated in great detail from a theoretical/numerical point of view. Scattered results have been presented in, for example, (Ref 2, 4) and also in more detail in (Ref 13). In the latter case, general residual (applied) surface stresses were considered. One important aspect of this is the influence on the invariance from elastic deformations. This is somewhat surprising as the few pertinent results that exist regarding this matter, cf. (Ref 12, 14), indicate that when elastic effects are noticeable, invariance is lost. This is not an issue for standard metallic materials, but could be so, for example, for polymers and ceramics where elastic deformations around the contact region are in the same order as the plastic ones. It is therefore the intention of the present paper to investigate this matter in some detail.

Theoretical Background

The theoretical foundation laid down in (Ref 4, 5, 12) will be relied upon for background. This foundation rests on the invariance of hardness which will be tested presently using the finite element method; in particular, the commercial package ABAQUS (Ref 15) is used.

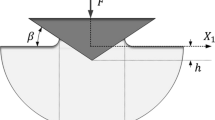
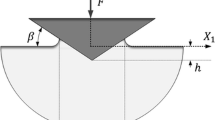
The analyses concern cone indentation with an angle β = 22° (corresponding to the angle at Vickers indentation), see Fig. 1, of elastic-ideally plastic materials. Plasticity is modeled using the standard Prandtl-Reuss (Mises) equations. Only homogeneous residual equi-biaxial stress fields are considered. The restrictions of the problem are introduced for clarity but not for necessity. The results will be correlated based on the well-known nondimensional strain parameter Λ suggested by Johnson (Ref 16, 17) according to

$$\varLambda = E\;{ \tan }\;\beta /(\sigma_{y} (1 - \nu^{2} ))$$
(1)

where E, ν and σ y are Young’s modulus, Poisson’s ratio and the initial material flow stress, respectively. It should be noted that in Eq 1, only elastic-ideal plasticity is considered, but this limitation can be taken care of by replacing σ y with the flow stress at a representative value of the effective plastic strain. Furthermore in (1), β is the angle between the sharp indenter and the undeformed surface of the material, as indicated in Fig. 1 for a cone indenter geometry. By using the Λ-parameter, Johnson (Ref 16, 17) also characterized three levels, see Fig. 2, of indentation (contact) behavior pertinent to the behavior of the material hardness H. These levels are: level I representing almost purely elastic indentation, level II representing a contact behavior where both elastic and plastic material properties are of importance and level III corresponding to a case where plasticity dominates the indentation problem (this level is at sharp indentation pertinent to most engineering metals and alloys).

Fig. 1
figure 1

Schematic of the geometry of the cone indentation test where a represents the true contact radius. In the present investigation, β = 22°. The nominal contact area A nom = πh 2/(tanβ)2 where h is the indentation depth

Full size image
Fig. 2
figure 2

Normalized hardness, \(\bar{H} = H/\sigma_{y} ,\) and area ratio, c 2, as functions of lnΛ, Λ defined according to Eq 1. Schematic of the correlation of sharp indentation testing of elastic-ideally plastic materials. The three levels of indentation responses, I, II and III, are also indicated. Approximately, level II contact initiates at Λ = 3 level III contact at Λ = 900. The \(\bar{H}\)-curve flattens out at (approximately) Λ = 30

Full size image

Based on extensive investigations, cf., e.g., (Ref 4, 5), it is properly confirmed that the material hardness is invariant of residual stresses at level III contact. Other global indentation properties do, however, show dependence of such stresses and of particular interest; then, the relative contact area is

$$c^{2} = A/A_{\text{nom}} .$$
(2)

In (2), the areas A (true contact area) and A nom (nominal contact area) are pertinent to projected contact areas, see Fig. 1. Note that c 2 = 1 when neither sinking-in nor piling-up occurs at the contact boundary.

This dependence was analyzed in (Ref 4, 5), and the formula

$$c^{2} = c^{2} (\varepsilon_{\text{res}} ,\sigma_{\text{res}} = 0){-}0.32{ \ln }(1 + (\sigma_{\text{res}} /\sigma_{y} (\varepsilon_{\text{res}} )))$$
(3)

was derived for the case of equi-biaxial residual stresses σ res and residual effective plastic strains ε res. Other parameters in (3) are: c 2(ε res, σ res = 0) is the c 2-value for a strained material with no residual stress and σ y (ε res) is the yield stress of the material exhibiting a residual effective plastic strain ε res. At ideal plasticity, Eq 3 becomes

$$c^{2} = c^{2} (\sigma_{\text{res}} = 0){-}0.32{ \ln }(1 + (\sigma_{\text{res}} /\sigma_{y} ))$$
(4)

due to the fact that the yield stress does not depend on the plastic strain state. It should be mentioned, as discussed in (Ref 11), that predictions made by Eq 3 and 4 are more accurate in tension than in compression.

The theoretical foundation for Eq 3 and 4 is the equivalence of mechanical fields close to the indenter in case of either contact-induced stresses in a virgin (unstressed) material or contact-induced stresses in a material with an initial material yield stress σ y  + σ res. This was shown in (Ref 4, 5) from numerical (FEM) simulations. Accordingly, using an apparent yield stress

$$\sigma_{{y,{\text{apparent}}}} = \sigma_{y} + \sigma_{\text{res}}$$
(5)

in Λ in Eq 1, according to

$$\varLambda = E{ \tan }\beta /(\sigma_{{y,{\text{apparent}}}} (1 - \nu^{2} )),$$
(6)

makes it possible to rely on the universal c 2-curve in Fig. 2 regardless if residual stresses are present or not. As a consequence, the universal c 2-curve in Fig. 2 can be used to determine σ res in a situation where c 2(σ res = 0) is known. The accuracy of this approach to residual stress determination is of course based on the finding that elasticity influences c 2 in a wider range of Λ-values than what is the case for the hardness, see Fig. 2.

However, the above discussed difference of mechanical behavior at tension and compression reduced the accuracy of the results when relying on Eq 4. For this reason, Rydin and Larsson (Ref 12) restudied the definition of σ y,apparent and it was found that general high accuracy was achieved by replacing Eq 5 with the expression

$$\sigma_{{y,{\text{apparent}}}} = \sigma_{y} + F\sigma_{\text{res}} ,$$
(7)

where

$$\begin{aligned} F = 0.52,\;\sigma_{\text{res}} < 0 \hfill \\ F = 1.77,\;\sigma_{\text{res}} > 0. \hfill \\ \end{aligned}$$
(8)

Explicitly, it was suggested in (Ref 12) that the relation

$$c^{2} = c^{2} (\sigma_{\text{res}} = 0) - 0.35{ \ln }(1 + (F\sigma_{\text{res}} /\sigma_{y} ))$$
(9)

should replace Eq 4 above. Physically, this should be interpreted in the way that any deviation in indentation parameter values, from the corresponding values for the virgin material, is due to residual stress effects. It was shown by Rydin and Larsson (Ref 12) that Eq 9 improved very much on the situation as compared with the results from Eq 4. High accuracy predictions in both tension and compression were achieved as depicted in Fig. 3 where excellent agreement should be noted.

Fig. 3
figure 3

Area ratio, c 2, as function of lnΛ, Λ defined according to Eq 6 with the yield stress σ y replaced by the apparent yield stress σ y,apparent in Eq 7. Cone indentation of elastic-ideally plastic materials is considered. The results are taken from Rydin and Larsson (Ref 12)

Full size image

As mentioned repeatedly above, the usefulness of Eq 9 rests on the hardness invariance. Otherwise, the solution approach becomes much more complicated as, for example, ε res in Eq 3 cannot be determined with any acceptable accuracy when strain-hardening effects are at issue. Even though invariance is firmly established, as discussed repeatedly above, there are also a few other studies, cf. (Ref 12, 14), indicating that when elastic effects are noticeable, invariance is lost. To clarify this matter is of considerable importance in this context and in particular then to correlate these findings with the Johnson (Ref 16, 17) parameter Λ. In doing so, the results by Rydin and Larsson (Ref 12) will be scrutinized, but also supplemented by presently performed finite element calculation to be described below.

Numerical Analysis

The numerical analysis rests on the finite element method. However, before discussing the discretization of the problem, the fundamental assumptions will be presented.

As stated repeatedly above, quasi-static cone indentation of elastic-ideally plastic prestressed materials is analyzed here. Relying upon classical elastoplasticity (Mises), this indicates that plastic deformations occur when

$$\sigma_{e} = \sigma_{y} .$$
(10)

The governing equations are formulated for large deformations (Ref 18), and accordingly, when the material is loaded elastically (or unloaded), the constitutive behavior is determined by Hooke’s law formulated hypoelastically. Furthermore, frictionless contact is assumed in the finite element calculations as it has been shown by, for example, Giannakopoulos and Larsson (Ref 19) and Carlsson et al. (Ref 20), that friction will have a very small influence on hardness and relative contact area.

The dicretization and finite element solution of the problem rests on the approach described in previous studies (Ref 19, 21-23). This procedure was further developed in (Ref 4, 5, 12) to also account for residual (applied) stresses. Accordingly, the foundation for the numerical analysis in the present paper is well established.

The finite element mesh used in the calculations is shown in Fig. 4. It goes almost without saying that axisymmetry is assumed. The entire mesh is shown in Fig. 4(a), and mesh details close to the indenter are shown in Fig. 4(b). In total, the mesh consists of 4567 four-noded axisymmetric hybrid elements and 4816 nodes. Hybrid elements were used in order to facilitate convergence at dominating plastic deformation.

Fig. 4
figure 4

Finite element mesh used in the numerical calculations. (a) Complete mesh. (b) Details close to the region of contact

Full size image

In order to introduce residual (applied) stresses, into the finite element simulations, the movement of the outer boundary of the mesh was prescribed by radial displacements u prior to indentation, see Fig. 5. During the indentation process, u was kept constant. With such a prestress (pre-deformation), axisymmetry still holds and equi-biaxility of applied stresses is ensured. It should be emphasized that the values on the radial displacements u are chosen in such a way that residual (applied) stresses are always in the elastic range.

Fig. 5
figure 5

Schematic of the pre-indentation loading. u is the prescribed radial displacement at the outer surface generating applied (residual) stresses

Full size image

The resulting set of governing equations were solved using the commercial finite element program ABAQUS (Ref 15). With a numerical solution to the problem obtained, the material hardness was calculated from the indentation load F and the projected contact area A, according to

$$H = F/A.$$
(11)

Results and Discussion

In the presentation below, the behavior of the material hardness at cone indentation of elastic-ideally plastic materials will be investigated in the presence of in-plane (X 1 − X 3-plane) equi-biaxial residual (or applied) stresses. The investigation is based on the finite element method and the material properties, and the residual fields are described by the Johnson (Ref 16, 17) parameter Λ, in Eq 1 and 6, and the stress ratio σ res /σ y . The efforts are mainly devoted toward an understanding of the behavior of the hardness, Eq 10, at level II indentation when the influence from elasticity is substantial. At level III indentation, it is well known, as discussed in detail above, that the hardness is invariant of residual stresses.

It seems appropriate to first of all discuss some previous results directly relevant for this investigation. This concerns some results by Rydin and Larsson (Ref 12) where the hardness was determined for the cases ln Λ = 3, 5 [Λ determined according to Eq 1 not accounting for the apparent yield stress in Eq 7] and for different values on the stress ratio σ res /σ y . A summary of the results by Rydin and Larsson (Ref 12) is shown in Fig. 6. Clearly, when ln Λ = 5, the hardness in Fig. 6(a) is as stated many times above, independent of the residual stress state. However, when ln Λ = 3, the hardness in Fig. 6(b) decreases substantially at tensile residual stresses. It should be noted that the horizontal line corresponds to the rigid-plastic (level III) solution determined by Atkins and Tabor (Ref 24) reading

$$H = 2.54\sigma_{y}$$
(12)

at cone indentation and to be compared with the famous Tabor (Ref 25) relation

$$H = 2.8\sigma_{y}$$
(13)

at rigid-plastic Vickers indentation.

Fig. 6
figure 6

Influence of residual stress on hardness values. Normalized hardness, H/σ y , as function of residual stress ratio, σ res /σ y . Cone indentation of elastic-ideally plastic materials is considered. The straight line represents Eq 12. The results are taken from Rydin and Larsson (Ref 12). (a) ln Λ = 5 where Λ is defined according to Eq 1. (b) ln Λ = 3 where Λ is defined according to Eq 1

Full size image

With the results in Fig. 6 in mind, it is illustrative to scrutinize hardness results presented in the same way as shown in Fig. 3 for the area ratio c 2 depicted as function of the Johnson (Ref 16, 17) parameter Λ [defined according to Eq 1]. This is done in Fig. 7 clearly showing the three levels of indentation schematically shown in Fig. 2 but now based on actual finite element results. Figure 7 shows that ln Λ = 3 constitutes an approximate border between level II and level III indentation. According to the results shown in Fig. 6(b), this transition occurs when ln Λ is slightly less than 3 when defining Λ according to Eq 6 with σ y,apparent according to Eq 7. Clearly, the results in Fig. 6 and 7 are in conformity and this will be further investigated in the spirit of the corresponding results for c 2 in Fig. 3 in the context of residual stresses.

Fig. 7
figure 7

Normalized hardness, H/σ y , as function of lnΛ, Λ defined according to Eq 1. Cone indentation of elastic-ideally plastic materials is considered. The straight line represents Eq 12. Stress-free results taken from Larsson (Ref 23)

Full size image

Consequently, in Fig. 8 the results in Fig. 6 and 7 are combined with Λ defined by Eq 6 with σ y,apparent according to Eq 7. Obviously, the (normalized) hardness values H/σ y fall on a single master curve, indicating that this parameter can be correlated with residual stresses in the same way as the area ratio c 2.

Fig. 8
figure 8

Normalized hardness, H/σ y , as function of lnΛ, Λ defined according to Eq 6 with the yield stress σ y replaced by the apparent yield stress σ y,apparent in Eq 7. Cone indentation of elastic-ideally plastic materials is considered. The straight line represents Eq 12. Open circle, stress-free results taken from Larsson (Ref 23). Filled circle, the hardness values in Fig. 6 with and without residual stresses

Full size image

From an analysis point of view, this is a remarkable finding as it indicates that all previously derived formulae, aiming at material characterization using indentation testing, can be applied also in case of residual stress determination by indentation. Indeed, this is so also at level II indentation where elastic effects are pronounced.

It should be admitted immediately that this conclusion rests on a few numerical results from Fig. 6. Accordingly, additional finite element calculations, as described above, were performed in order to confirm this finding. The materials investigated in this case were defined by

$$\ln\,\varLambda = 3.4,\;3.52$$
(14)

with the Johnson (Ref 16, 17) parameter Λ defined according to Eq 1. These rather close values were chosen in order to secure that the stress-free material was pertinent to level III contact while the behavior entered the level II regime in the presence of tensile residual stresses. As regards residual stresses, the values

$$(\sigma_{\text{res}} /\sigma_{y} ) = 0,\;0.25,\;0.375,\;0.5,\;0.75,\;1.0$$
(15)

were chosen (not all combinations of the parameters in Eq 14 and 15 were investigated). Obviously, only tensile residual stresses are considered for the reason that compressive ones would increase Λ, when defined according to Eq 6 and 7, leading to a more pronounced level III (rigid-plastic) situation.

The present numerical results based on Eq 14 and 15 are introduced in Fig. 9 and 10, and again, these results indicate that also in this case ln Λ = 3 constitutes an approximate border between level II and level III indentation and that the explicit hardness values fall right on the master curve defined by the stress-free hardness values in Fig. 7, see especially Fig. 10. The latter finding is true for both new level II and level III results.

Fig. 9
figure 9

Influence of residual stress on hardness values. Normalized hardness, H/σ y , as function of residual stress ratio, σ res /σ y . Cone indentation of elastic-ideally plastic materials is considered. The straight line represents Eq 12. The present results for the material and residual stress state defined in Eq 14 and 15

Full size image
Fig. 10
figure 10

Normalized hardness, H/σ y , as function of lnΛ, Λ defined according to Eq 6 with the yield stress σ y replaced by the apparent yield stress σ y,apparent in Eq 7. Cone indentation of elastic-ideally plastic materials is considered. The straight line represents Eq 12. Open circle, stress-free results taken from Larsson (Ref 23). Filled circle, the hardness values in Fig. 6 with and without residual stresses. Asterisk, the hardness values in Fig. 9 with and without residual stresses

Full size image

Consequently, it can be stated that with Λ defined by Eq 6, with σ y,apparent according to Eq 7, both hardness and area ratio c 2 can be directly correlated with stress-free master curves for these quantities. This is indeed valid in the entire range of indentation values pertinent to different levels of indentation.

The present finding is indeed an encouraging one, when it comes to residual stress determination by sharp indentation, as it suggests that also the hardness value (and not only the area ratio c 2) can be used for such a purpose. As already mentioned above, this is especially attractive as it indicates that the wealth of characterization formulas pertinent to indentation hardness is available also for the purpose of residual field determination. It should be emphasized though this additional information is only available at level II indentation. At the level III indentation, the (normalized) hardness is independent of the Johnson (Ref 16, 17) parameter Λ, see Eq 12 and 13, and consequently invariant of residual stresses as discussed extensively and in detail above. This feature naturally also brings up the problem of demarcating between level II and level III indentation. An obvious partial remedy to this is of course to carefully characterize the virgin material and to determine where the corresponding Λ-value falls on the hardness curve in Fig. 7. In addition, adherence to Eq 12 (Ref or Eq 13) also indicates if level II or level III indentation is at issue. Also the value on the area ratio c 2 can give further information regarding this issue.

Obviously, the analysis above is restricted to cone indentation of elastic-ideally plastic materials with equi-biaxial residual stress fields. This is not a major issue though as an extension of the theoretical foundation to successfully include also plastic strain-hardening, general biaxial stresses as well as other indenter geometries have been extensively discussed in, for example, (Ref 5, 26). The practical details of this matter are left for future studies.

Finally, it is worth mentioning that the present approach could very well be applied to other types of contact problems. One of these problems could be scratching and scratch testing where correlation of material and contact properties, in the spirit of Johnson (Ref 16, 17), has been discussed for some time now, cf. (Ref 27-35). It remains, however, to undertake an analysis that incorporates also residual stresses in this special type of global quantity correlation.

Conclusions

Cone indentation of elastic-ideally plastic materials has been investigated numerically, using the finite element method, and theoretically. The most important findings can be summarized as follows:

  • The global indentation properties, hardness and contact area ratio can be completely correlated using a single nondimensionalized strain parameter regardless if residual stresses are present in the material or not.

  • This correlation is achieved by accounting for residual stress in the definition of the material yield stress.

  • This result creates new possibilities of practical importance for residual stress determination by sharp indentation testing when elastic and plastic deformations induced by indentation are of equal magnitude as an abundance of formulas used for material characterization using indentation is available also when it comes to determination of residual stresses.

  • At rigid-plastic indentation, i.e., negligible elastic deformations, the hardness is, as determined also in previous studies, invariant of residual stresses and only the contact area ratio is available for the determination of such mechanical fields.

The theoretical foundation necessary to incorporate also plastic strain-hardening, general biaxial stresses as well as other indenter geometries, has been laid down in previous studies, but the details pertinent to such an analysis specifically related to the present findings are left for future studies.