Abstract
SnxSb20Se80−x bulk glasses were prepared using the well-known melt quenching technique, where x was taken as 7.5 at.%, 9.5 at.%, 11.5 at.% and 13 at.%. X-ray diffraction (XRD) and differential scanning calorimetery (DSC) were used to monitor the crystallinity and transition temperatures, respectively. XRD examinations showed that the 7.5 at.% and 9.5 at.% compositions were purely amorphous, while the other two compositions exhibited a crystalline structure. DSC thermograms demonstrated that 7.5 at.% and 9.5 at.% alloys had a single crystallization peak, whereas for the 11.5 at.% and 13 at.% alloys, two exothermic peaks and three peaks appeared. The glass stability and kinetics of amorphization and crystallization were studied using different approaches. The correlation between topological constraints and the dimensionality of the growth was established.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Many applications are based on chalcogenide glasses.1 Because of their academic and applied potential, Sn–Sb–Se glasses have attracted wide research attention, especially for infrared photonic applications.2,3 The correlation between infrared response and other properties has been investigated.3,4
Thermal analysis is a fundamental tool that is commonly used for studying glasses. Combined with x-ray diffraction (XRD), microscopy and spectroscopy complete the determination of transition points and structure.5 Moreover, electrical conductivity has confirmed the thermal properties of the glass.6 Many theories have been developed to understand the nature of glasses, with the result that their behavior can be predicted.1,5 However, some rules have been violated, and discrepancies in results have been found in the literature. For example, Imran7 reported one-dimensional growth of the Sn–Sb–Se system, while Kumar et al. reported three-dimensional growth.8 In addition, the boundaries of the vitreous domain may differ, and so interpretation of the results may disagree. This can occur for many reasons; one of the most important issues is the preparation procedure, mainly the thermal heating protocol and the quenching method.9,10 Sovoboda and Malek11,12 attempted to compile a unified set of standards of the processes involved in non-isothermal studies of glasses. Instrumental effects were considered in their studies.11,12
However, the substantial agreement among the efforts of different groups suggests that their efforts may integrate.1,5 For example, the dimensionality of the growth which has been determined based on temperature can be determined based on time, as can the activation energy.13 The relationship between the structure and properties is the core of materials science. In glasses, tuning the composition induces topological changes which in turn affect the properties and hence the potential applications of the glasses.2,3 The effect of Sn and/or Sb addition on the properties of a Se-based alloy has been studied before.2,3,7,8,9,10 However, conflicting results have been obtained regarding the compositional effect on the glass formation domain and the nature of the growth. For example, is the growth one- or three-dimensional?7,8
Regarding these facts, different considerations were taken in the present work. We carried out systematic experiments via XRD and thermal analysis for studying the thermal stability and crystallization kinetics in the SnxSb20Se80-x alloy system. The relationship between the structure and thermal properties of these alloys was also investigated, and the compatibility between growth parameters was assessed.
Materials and Methods
Granules of Sb, Se and Sn with 5N purity were used. Weighing of the materials was done according to the atomic percentages of the elements. The weighed quantities were sealed in quartz tubes under vacuum of 10−3 mbar. The sealed tubes were placed in a furnace and the furnace was heated to 860°C at a heating rate of 4°C/min. The tubes were agitated once each hour for 12 h, at the highest temperature in order to achieve good homogeneity. The structure of the prepared samples was investigated using a high-resolution XRD system (PANalytical X'Pert Pro, Malvern Panalytical, UK) with CuKα radiation, λ = 1.5406 Å, operated at 45 kV and 30 mA. The XRD patterns were recorded in the 2θ range of 5°–80°. The differential scanning calorimetry (DSC) measurements were performed on a Shimadzu DSC-50 differential scanning calorimeter with scanning rates of 10 °C/min, 20 °C/min, 25 °C/min and 30 °C/min. The measurements were performed under a flow of dry nitrogen gas at a rate of 50 ml/min. The data were calibrated using the melting transition of indium at 157°C.
Results and Discussion
XRD Studies
XRD diffractograms are presented in Fig. 1. The amorphous nature can be clearly seen in the two compositions of Sn7.5Sb20Se72.5 and Sn9.5Sb20Se70.5. The crystallinity appears at the higher Sn content. The two crystalline patterns are identical with differences in the peak intensities and the appearance of a three extra peaks in the highest Sn content alloy. Examination of the powder diffraction files reveals that more than one phase exists. The peaks of the present samples match JCPDS card numbers 23-0602 and 75-1462 for SnSe2 and Sb2Se3, respectively.
Many groups have studied this alloy with different compositions. Adam et al.2 mapped a ternary plot based on XRD results and theoretical models. Kumar and Thangaraj9 found that Sn concentrations from 8 at.% to 18 at.% led to vitrification of the corresponding alloys. Adam et al.2 and Wakkad et al.9 reported that a mixed amorphous-crystalline phase appeared at 12 at.% Sn and complete crystallization took place at 13 at.%. While Xue et al.3 reported that Sb2Se3 is the first separated phase, others9 suggest that it is SnSe2. Adam et al.14 reported that, besides the two binary phases, ternary phases can exist in the crystalline state.
DSC Results
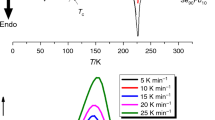
Figure 2 presents the Sn9.5Sb20Se70.5 glass thermograms, where one can see a glass transition step, a crystallization exothermic peak and a melting endothermic peak in each thermogram. Similar results were obtained for the Sn7.5Sb20Se72.5 glass. Figure 3 shows a glass transition temperature and two crystallization temperatures for the Sn11.5Sb20Se68.5 composition. For the Sn13Sb20Se67 alloy, there are three crystallization peaks. At 20 and 25 K/min heating rates, three peaks appear, and two of them merge to a single peak at a heating rate of 30 K/min. The values of transition temperatures are presented in Tables I, II and III.
In this study, XRD and DSC results confirm that both phases coexist in an amorphous matrix at Sn content of 11.5 at.% and 13 at.%. Phase separation by annealing was reported by Xue et al.3. Phase separation by changing the composition constituents has also been reported. For instance, Kumar et al.8 found that the common peak of the separated phases and the single phase peak for their thermograms was the high-temperature peak. In this study, however, the low-temperature peak is common, as shown in Fig. 4. DSC results suggest that samples which contain 11.5 at.% and 13 at.% Sn show peaks due to the two common phases, and the third may be due to Sn2Sb4Se8 phase or similar ternary alloys. Cards of the three phases show similar peaks. See, for example, JCPDS card numbers 36-1207, 36-1206, 23-0602, 89-3197, 89-0821 and 75.1462. In other words, they may overlap and/or coexist, but DSC results confirm that coexistence.
Effects of Sn Addition
Covalent bonding is the most likely in these compositions.15 During preparation, the Sn content affects the three linked quantities: the average coordination number, the fraction of bonds and the overall mean bond energy. The average coordination number is given by2
where 4, 3 and 2 are the coordination numbers of Sn, Sb and Se atoms, respectively, and x, y and z are their mass percentages. Table IV shows that \(\mu \) values vary around 2.4, which has theoretical importance and has been verified experimentally.3
The fraction of the bonds was calculated from the chemical order model according to the following Eq. 2:
As seen in Table IV, the Sn–Se does not exceed the 44.5% upper limit for the previously reported glass transition.2 The fraction of Se–Sb bonds decreases much more slowly than that of Se–Se bonds with the increase in the Se-Sn bond fraction, as a result of the increase in the Sn content.
The overall mean bond energy can be calculated from15:
where \(\left\langle {E_{{{\text{cl}}}} } \right\rangle\) is the mean bond energy of the average cross-linking per atom and \(E_{{{\text{rm}}}}\) is the average bond energy per atom of the remaining matrix.
\(\left\langle {E_{{{\text{cl}}}} } \right\rangle\) is given by
where Dcl is the cross-linking parameter and \( E_{{{\text{hp}}}}\) is the average heteropolar bond energy.
The energies of the involved bonds are 138.92, 195.98 and 187.6 kJmol−1 for the D(Se–Se), D(Se–Sn) and D(Se–Sb), respectively.7
From Table IV, it can be seen that the cross-linking parameter, the average cross-linking energy and the overall mean bond energy increase with the increase in Sn content, while the average remaining matrix energy decreases.
The ratio of the covalent bonding possibilities of chalcogen atoms to those of non-chalcogen atoms which determine the deviation in stoichiometry and is given by the symbol r is presented in Table IV. The values of r indicate chalcogen-rich alloys.9
From the thermograms (Figs. 2, 3 and 4) and Tables I, II and III it is clear that Tɡ increases with the increase in Sn content. This can be explained as follows: the increase in Sn content increases the average coordination number, the cross-linking parameter and the mean overall bond energy. It has been reported that bonds saturate in descending order according to their energy values.16 The bond energy of Se-Sn is higher than that of Se–Se, so the mean bond energy of the average cross-linking per atom, \({E}_{hp}\), will increase. Simultaneously, the decrease in the number of Se–Se bonds will enhance cross-linking and reduce the average energy of the remaining matrix. Due to the increase in the Sn content, the 2-coordination-number Se is replaced by the 4-coordination-number Sn. The probability of formation of local SnSe4/2 tetradedral structural units increases with the increase in Sn content which has been verified experimentally for similar compounds.17 And as a result, Tɡ and the overall mean energy \(\langle E\rangle \) increase.
Glass-Forming Ability and Thermal Stability
Tables I, II and III summarize the characteristic temperatures obtained from DSC thermograms of the compositions S9.5Sb20Se70.5, Sn11.5Sb20Se68.5 and Sn13Sb20Se67 at the stated heating rates. By increasing the heating rate, the onsets, peaks, and end sets of glass transition, crystallization, and melting shifts towards higher temperatures. These shifts can be explained on the basis of the reduction of time needed to complete the corresponding processes. For example, because the glass did not take enough time to transform, the alloy resistance to crystallization increases with the increase in heating rate.13 Figure 2 shows DSC thermograms of the Sn9.5Sb20Se70.5 composition at different heating rates. Similar curves were obtained for the composition Sn7.5Sb20Se72.5. Data are shown in Fig. 3 for the Sn11.5Sb20Se68.5 alloy. It can be clearly seen that this composition shows two crystallization peaks. Figure 4 shows DSC thermograms for the Sn13Sb20Se67 composition. The ease with which the melt vitrifies without crystallization is referred to as the glass-forming ability (GFA). This has been linked to devitrification experiments by the quantity \(\Delta T\).13
The reduced transition temperature of glass, \({T}_{rg}\), is related to the GFA.
\({T}_{rg}\) was found to be inversely proportional to the crystallization rate. In this study the values are close to 2/3, which is slightly smaller than those obtained by Farid and Aly.18 The Se content in their glasses was high.
Glass-forming tendency can be manifested by another parameter called the Hruby number, Hr, where \(\Delta T\) can be normalized to take the form13:
Here, the quantity \(\Delta T\) is directly proportional to the GFA, while the denominator is indirectly proportional to it. When the crystallization peak shifts, Hr moves more rapidly.\({H}_{r}\) values increase with an increasing heating rate, which can be seen clearly from Tables I, II and III.
Saad and Poulain19 suggested the S parameter of stability, which does not include the melting point temperature and can be used for comparisons between different compositions at the same heating rate.
From Tables I, II and III, it can be said that the S parameter increases for the same composition with the increase in the heating rate, but the increase is not straightforward. At least one value disrupts that increase. Finally, one can observe that the 9.5 at.% Sn composition has the highest values of \(\Delta T\), Trg, S and \({H}_{r}\), followed by the 7.5 at.% Sn composition and finally the 11.5 at.% Sn composition. Thus, the stability follows the same order.
T ɡ Heating Rate Dependence
Tables I, II and III indicate that with an increase in the heating rate, the glass transition temperature increases. This behavior can be verified by the following equation.13
This behavior is clear in Fig. 5. Therefore, this study predicts that at a heating rate of 1 K/min, the glass transition temperature will be 119.92 °C, 145.93 °C and 175.95 °C for the 7.5, 9.5 and 11.5 at.% compositions, respectively. B is a composition-dependent constant.
Activation Energy of Glass Transition and Index of Fragility
Structural unit rearrangements are associated with the transformation from the glass to the amorphous state. The time required to undergo this process is called the relaxation time, which is dependent on the thermal history. The thermal history includes, for example, the cooling rate, heating rate, and annealing time and pressure.13 Moynihan and Kissinger developed two methods to calculate the activation energy of amorphization (Eɡ) (i.e. activation energy of glass transition).13 Moynihan's method depends on the thermal history of the sample. Equations 9 and 12 were used to calculate the activation energy of amorphization according to these methods. Their values were calculated using Fig. 6 and are listed in Table V.
The other one is termed Kissinger's method. Its derivation was based on considering the quantity of transformed fraction and the activation energy.13 The transformation has been considered as a first-order transition obeying Eq. 10.
where k is an Arrhenius-type reaction rate
where E is the energy of transformation, R is the universal gas constant, and \({k}_{o}\) is a frequency factor. This method has been used in amorphization and crystallization.13 It was used to calculate the activation energy of the glass transition in this study and many other studies13,16:
Many theories have been put forth discussing the glass transition phenomenon.1,5 Viscosity and entropy are involved in many of them. Configurational degrees of freedom are frozen at a certain temperature according to the Vogel–Tamman–Fulcher (VTM) equation.1 Below Tɡ, only vibrational entropy can be considered. Therefore, heating defreezes the glass and allows it to rearrange to minimize its energy.
Viscosity and the relaxation time can be linked to the dynamics of structural relaxations above Tɡ. If their dependence on temperature is of an Arrhenius type, then the activation energy is constant and the corresponding supercooled liquid is strong. If not, then it will be fragile.20
The VTM relationship can be used to give the fragility index, which can be determined in terms of the activation energy of glass transition as follows20:
By using the values of glass activation energies determined by Moynihan's method, the values of \({m}_{F}\) were calculated as shown in Tables I, II and III. It is clear that the obtained alloys are strong glass formers. The strongest of them has the lowest Sn content. This result agrees with the 2/3 rule mentioned earlier.
Activation Energy of Crystallization
Crystallization takes place because of heating. The energy required to induce the amorphous-to-crystal transition is called the activation energy of crystallization, Ec. There is a similarity between the final equations used to estimate the activation energies of amorphization and crystallization. For example, peak shift methods were used in both calculations.1,13 Also, Eq. 9, which gives Ec according to Mahadevan's method, is similar to that of Moynihan, which was used above to calculate the activation energy of the glass transition. The Kissinger method uses the same formula, except that it replaces \({T}_{g}\) with \({T}_{p}\), as shown in Eq. 15. A fundamental equation in studying transformation kinetics was given by Avrami for the rate of the transformed fraction, which takes the form
Using Eqs. 11 and 14 Augis and Bennett modified Kissinger formula (Eq. 16) to be written as Eq. 17.13
Activation energies of crystallization by these methods are drawn in Fig. 7 and presented in Table V. Crystallization is a disorder-to-order structural relaxation, where disordered bonds change into an ordered network. According to the temperature-based methods, the activation energy of crystallization decreases with the increase in the Sn content as shown in Table V. This result disagrees with that reported by Kumar et al.8 This may be explained in the difference between the two states. The energy barrier between the two configurations (ordered and disordered) decreases with the increase in Sn content due to the partial crystallinity. Fragility index shows that the 9.5 at.% Sn is the strongest glass former, so it supposed to have the highest crystallization energy. In the same time, there are no peaks in the XRD at this concentration. XRD and DSC results show that the 11.5 at.% Sn composition is a glass-crystal matrix, so the energy of transformation should be the lowest. On the other hand, the corresponding XRD reported by Kumar and Thangaraj10 does not show any peaks.
Temperature-Based Reaction Order
Matusia et al. developed a method for calculating the dimensionality of the growth and the effective activation energy of crystallization for non-isothermal phase transformations.13
where n is the Avrami index or the order of the reaction, and m represents the dimensionality of the growth.13 The values of n in this study are given in Table VI, where n and m are related by n = m + 1 or n = m, and its value ranges from 1 to 4. If nucleation exists for some reason before thermal analysis, m will equal n. Nucleation and growth are involved in crystallization. Saturation of the nucleation centers at higher temperatures causes nonlinearity of relationship 15 at constant heating rates.21 This might explain some of the curves in this study as shown in Fig. 8.
Time-Based Reaction Order and Activation Energy of Crystallization
Avoiding the Avrami number, Afify13 used Eq. 11 to estimate the value of the crystallization activation energy. When the transformed fraction reaches about 0.63, the reaction rate can take the following form:
Plotting \({\mathrm{ln}(k}_{0.63})\) versus \((1/{T}_{063})\) as shown in Fig. 9 and presented in Table III, Ec values are determined. The trend of the calculated values is not significant. Equation 14 was used to obtain the reaction order n as follows. The corresponding plots are shown in Fig. 10.
At the temperatures presented, n values for different compositions determined by this method are shown in Table VI, where n values determined by the Afify method confirm the values obtained by the temperature-based method.
From the above analysis, three-dimensional growth is suggested in this study. This result agrees with some reports in literature concerning the same compound.8 The number of degrees of freedom equals the dimensionality m obtained above.1 Two equations have been used to correlate the dimensionality to the average coordination number.1,2,5
where Nco stands for the number of constraints. Equation 21 gives a sharp value of 2.4 for \(\mu \), while Eq. 22 yields an approximate number of 2.449. From Table IV, our results cover both these values. There is debate in the literature between the fixed value and the extended domain.1 The idea of an intermediate and self-organized phase was proposed and experimental verifications have been reported for values below and above 2.4.22,23,24,25,26,27,28,29
In this study, the best glass former has an average coordination number of 2.35, and the value corresponding to the most stable glass is 2.39. Crystallinity begins at 2.43. Thus, Eqs. 21 and 22 may combine and extend. There is a range of percolative transition, but the best glass may be obtained at 2.4. The percolative transition from floppy to rigid has been confirmed experimentally for the given system and the transition onset was less than 2.4.3
Conclusion
Sn content was changed in the SnxSb20Se 80−x alloy system, where x = 7.5, 9.5, 11.5 and 13 at.%. Materials with the first two percentages were completely amorphous while the other two were mixed glass–crystalline. According to DSC and XRD investigations, the crystalline phase itself is a mix of two or three crystalline phases. As Sn content increases, the mean coordination number, overall mean bond energy and the transition temperatures increased. Moreover, the increase in the Sn content induced crystallinity. At higher Sn content, the glass transformed to crystalline phases. The crystalline phase was grown in three dimensions. Using the theory of constraints, the glass shows a continuous change in the mean coordination number from the glass to the glass–crystalline alloy.
References
K. Tanaka and K. Shimakawa, Amorphous Chalcogenide Semiconductors and Related Materials (Cham: Springer, 2011).
A.B. Adam, S. Sakrani, and Y. Wahab, Glass-formation region of ternary Sn-Sb-Se-based chalcogenide glasses. J. Mater. Sci. 40, 1571 (2005).
X. Xue, F. Chen, C. Lin, R. Lin, X. Zhang, S. Dai, X. Zhang, and W. Ji, Microhardness and optical property of chalcogenide glasses and glass-ceramics of the Sn–Sb–Se ternary system. J. Am. Ceram. Soc. 102, 2066 (2019).
R. Lin, F. Chen, X. Zhang, Y.G. Huang, B. Song, S. Dai, X. Zhang, and W. Ji, Mid-infrared optical properties of chalcogenide glasses within tin-antimony-selenium ternary system. Opt. Express 25, 25674 (2017).
K.J. Rao, Structural Chemistry of Glasses (London: Elsevier, 2002).
A.K. Tammam, Z. Kahlifa, and S.A. Elsayed, First and second phase transition discovery in amorphous chalcogenide Se60Te30S10composition. J. Non-Cryst. Solids 529, 119729 (2020).
M.M.A. Imran, Thermal characterization of Se85-xSb15Snx(10≤x≤13) chalcogenide glasses. Physica B 406, 4289 (2011).
P. Kumar, J. Kumar, and R. Thangaraj, Phase separation phenomena in Sn-Sb-Se glassy semiconductors. Eur. Phys. J. Appl. Phys. 38, 1 (2007).
M.M. Wakkad, EKh. Shokr, H.A. Abd El Ghani, and M.A. Awad, Structural and kinetic evaluation of Sn–Sb–Se alloys. J. Phys. D: Appl. Phys. 40, 7578 (2007).
P. Kumar and R. Thangaraj, Glassy state and structure of Sn–Sb–Se chalcogenide alloy. J. Non-Cryst. Solids 352, 2288 (2006).
R. Svoboda and J. Málek, Thermal behavior in Se-Te chalcogenide system: interplay of thermodynamics and kinetics. J. Chem. Phys. 141, 224507 (2014).
R. Svoboda and J. Málek, Is the original Kissinger equation obsolete today? J. Therm. Anal. Calorim. 115, 1961 (2014).
Z.S. Khalifa and S.A. Elsayed, Non-isothermal crystallization kinetics of ternary Se60Te30S10 glass. Surf. Rev. Lett. 29, 2250024 (2022).
A.B. Adam, S. Sakrani, and Y. Wahab, Sn–Sb–Se crystalline phases formed by melt-quenching technique. J. Mater. Sci. 41, 5797 (2006).
L. Tichy and H. Ticha, Covalent bond approach to the glass-transition temperature of chalcogenide glasses. J. Non-Cryst. Solids 189, 141 (1995).
K.A. Aly, A.A. Othman, and A.M. Abousehly, Effect of Te additions on the glass transition and crystallization kinetics of (Sb15As30Se55)100−xTex amorphous solids. J. Alloys Compd. 467, 417 (2009).
Z. Wang, C. Tu, Y. Li, and Q. Chen, The effects of Sn and Bi additions on properties and structure in Ge-Se-Te chalcogenide glass. J. Non-Cryst. Solids 191, 132 (1995).
F.M. Abdel-Rahim and K.A. Aly, Structure and thermal analysis of Se100−x(SbSn)x chalcogenide glasses. J. Non-Cryst. Solids 419, 69 (2015).
M. Saad and M. Foulâin, Glass forming ability criteria. Mater. Sci. Forum 19–20, 11 (1937).
A.A. Abu-Sehly and A.A. Elabbar, Effect of long-term physical aging on the kinetic parameters in a common pharmaceutical drug: Flutab. Physica B 406, 319 (2011).
H.E. Atyia and A.S. Farid, Non-isothermal crystallization kinetics of ternary Se90Te10−xPbx glasses. J. Cryst. Growth 436, 125 (2016).
X. Feng, W.J. Bresser, and P. Boolchand, Direct Evidence for Stiffness Threshold in Chalcogenide Glasses. Phys. Rev. Lett. 78, 4422 (1997).
D. Selvanathan, W.J. Bresser, and P. Boolchand, Stiffness transitions in SixSe1−x glasses from Raman scattering and temperature-modulated differential scanning calorimetry. Phys. Lett. B 61, 150061 (2000).
D.G. Georgiev, P. Boolchand, and M. Micoulaut, Rigidity transitions and molecular structure of AsxSe1−x glasses. Phys. Lett. B 62, 9228 (2000).
P. Boolchand, D.G. Georgiev, T. Qu, F. Wang, L. Cai, and S. Chakravarty, Nanoscale phase separation effects near r =2.4 and 2.67, and rigidity transitions in chalcogenide glasses. C R Chimie 5, 724 (2002).
S. Chakravarty, R. Chbeir, P. Chen, M. Micoulaut, and P. Boolchand, Correlating melt dynamics and configurational entropy change with topological phases of AsxS100−x glasses and the crucial role of melt/glass homogenization. Front. Mater. 6, 166 (2019).
M.F. Thorpea, D.J. Jacobs, M.V. Chubynsky, and J.C. Phillips, Self-organization in network glasses. J. Non-Cryst. Solids 266–269, 859 (2000).
M.M. Wakkad, EKh. Shokr, and S.H. Mohamed, Crystallization kinetics and some physical properties of as-prepared and annealed Ge-Sb-Se chalcogenide glasses. Phys. Stat. Sol. A 183, 399 (2001).
M.M. Wakkad, EKh. Shokr, and S.H. Mohamed, Optical and calorimetric study of Ge-Sb-Se glasses. J. Non-Cryst. Solids 265, 157 (2000).
Acknowledgments
The authors would like to thank Prof. Samy Abdel-Hakim, Dr. Asma Abou Taleb and Dr. Aymen Amin for their efforts.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khalifa, Z.S., Mohamed, S.H. Effect of Sn Concentration on the Structural and Thermal Properties of SnxSb20Se80−x Glasses. J. Electron. Mater. 52, 7920–7930 (2023). https://doi.org/10.1007/s11664-023-10709-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11664-023-10709-y