Hot Extruded Bulk Polycrystalline (Bi_1-xSb_x)₂(Te_1-ySe_y)₃ Alloys: Electron Transport and Lattice Thermal Conductivity

Abstract

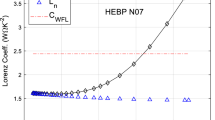
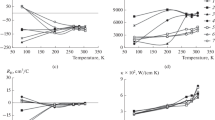
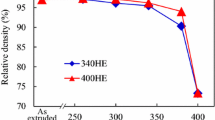
Hot extruded bulk polycrystalline n-type (Bi_1-xSb_x)₂(Te_1-ySe_y)₃ quaternary alloys with low Sb and Se concentrations (< 10%) are anisotropic materials by virtue of their texture which is a result of severe shearing involved in the extrusion process. Harman-type measurements have provided the electrical and thermal conductivity, Seebeck coefficient, and thermoelectric figure of merit parallel to the extrusion axis, as a function of temperature, in the range ~ 220–420 K. Mobility and carrier concentration were determined by Hall effect measurements along a plane perpendicular to the extrusion axis in the range 15–420 K. Modeling the electronic transport properties allows the determination of the total (including thermodiffusion) electronic contribution to the thermal conductivity. Thus, the lattice thermal conductivity $\kappa_{\parallel }^{{}}$, along the extrusion axis, can be obtained with a reasonable degree of accuracy in the range 220–380 K. The results carry a rather large relative uncertainty at higher temperatures as $\kappa_{\parallel }^{{}}$ decreases with increasing temperature with a tendency which mimics that observed for the crystalline base compound Bi₂Te₃.

Appendices

Appendix A

Review of the Electron Transport Model of HEBP Alloys

The transport model applicable at low applied electric fields and temperature gradients recognizes the importance of obtaining the most accurate description possible of the near equilibrium charge carrier chemical potential $\zeta$ relative to one of the band edges as a function of temperature. In the case of n-type semiconductors, the quantity $\Delta_{c} \equiv \zeta - E_{c0}$ is introduced, where $E_{c0}$ is the conduction band edge at the minima points ${\varvec{K}}_{{0i_{c} }}$ ($i_{c} = 1,2...N_{{V_{c} }}$) in K-space, where $N_{{V_{c} }}$ is the number of valleys in the conduction band. The quantity $\Delta_{c} \left( T \right)$ is obtained as a function of temperature by solving the neutrality equation including electron ionized deep traps:

$$ n - p = N_{d}^{\left( + \right)} - N_{a}^{\left( - \right)} = N_{d}^{sh} - N_{a}^{{}} + N_{D}^{ + } = N_{res} + N_{D}^{ + } $$

(A-1)

The residual carrier concentration $N_{res} = N_{d}^{sh} - N_{a}^{{}}$ is a constant controlled only by shallow donor doping of concentration $N_{d}^{sh}$ and possible acceptor impurities. The approximation of fully ionized shallow donors and of (all) acceptors in Eq. (A-1) restricts the validity of the approach to a limited temperature range where they are fully ionized, so this approximation cannot hold for very low temperatures (< 10 K).

$N_{D}^{ + }$ represents the ionized density of deep donors with energy levels $E_{D} = E_{c0} - \varepsilon_{D}$ deep within the gap, whose total concentration is $N_{DD}^{{}}$, or $N_{D}^{ + } = f_{DD}^{( + )} N_{DD}^{{}} = \left( {1 + 2\exp \left( {\frac{{\Delta_{c} + \varepsilon_{D} }}{{k_{B} T}}} \right)} \right)^{ - 1} N_{DD}$.

The solution of the neutrality equation (A-1), found in semiconductor physics, can be obtained using any computational tool providing a routine to numerically find the roots of a non-linear function of one variable, such as the “fzero” script in MATLAB.

The dispersion relation near the band edges is written as:

$$ E_{c} \left( {\user2{x,K}} \right) = E_{c} \left( {\user2{x,K}_{{0i_{c} }} } \right) + \varepsilon \left( {\user2{K - K}_{{0i_{c} }} } \right) = E_{c} \left( {\user2{x,K}_{{0i_{c} }} } \right) + \varepsilon \left( {\varvec{k}} \right), $$

(A-2)

where $E_{c} \left( {\user2{x,K}_{{0i_{c} }} } \right) = E_{c0} - \left| e \right|\psi \left( {\varvec{x}} \right)$ and $\psi \left( {\varvec{x}} \right)$ is the electric potential. This model is based on the assumption that for quaternary alloys whose composition is close to the base compound Bi₂Te₃ (small concentrations of Sb₂Te₃ and Bi₂Se₃) $\varepsilon \left( {\varvec{k}} \right)$ can be approximated by the non-parabolic form¹⁷:

$$ {{\hbar^{2} {\varvec{k}}_{{}}^{2} } \mathord{\left/ {\vphantom {{\hbar^{2} {\varvec{k}}_{{}}^{2} } {2m_{n}^{*} }}} \right. \kern-\nulldelimiterspace} {2m_{n}^{*} }} = \varepsilon \left( {1 + \lambda \varepsilon } \right) $$

(A-3)

The parameter $\lambda \left( T \right)$ is in general a function of the absolute temperature T and is taken as the inverse of the energy gap $E_{g} \left( T \right) = \Delta_{g0} - c_{T} T$ of the material, which has a constant temperature coefficient $c_{T}$. A corresponding expression is proposed for the dispersion relation of holes in the valence band. These assumptions are expected to apply for an energy range within 0.1 eV of the band edges and are based on an approximation of the DOS provided by ab initio calculations of the base compound,³¹ which is expressed as:

$$ D\left( \varepsilon \right) = \frac{{\sqrt 2 \left( {m_{c}^{DOS} } \right)^{3/2} }}{{\pi^{2} \hbar^{3} }}\left( {\varepsilon + \lambda \varepsilon_{{}}^{2} } \right)^{\frac{1}{2}} \left( {1 + 2\lambda \varepsilon } \right)\Theta \left( \varepsilon \right) $$

(A-4)

where $\Theta \left( \varepsilon \right)$ is the unit step function.

A second important assumption concerns the anisotropy of HEBP alloys and proposes and anisotropic one-particle distribution function as a solution of the Boltzmann transport equation in the form of a diagonal matrix with two equal components describing transport in the plan perpendicular to the extrusion axis $g_{ \bot ex} \left( {\user2{x,K}} \right) = g_{ \bot } \left( {\user2{x,K}} \right)$. The third diagonal element $g_{\parallel } \left( {\user2{x,K}} \right)$ corresponds to transport along the extrusion axis. The properties of interest are calculated using $g_{ \bot } \left( {\user2{x,K}} \right)$, since there is empirical evidence that motion along the extrusion axis differs from perpendicular transport by a constant factor. As will be shown, for the quaternaries of interest here this constant factor applies to the temperature range ~ 220–400 K, where only one scattering mechanism prevails, and in this range $g_{\parallel } \left( {\user2{x,K}} \right) \approx f_{an} g_{ \bot } \left( {\user2{x,K}} \right)$. For more specific details of the model, please see Section 2 of Masut et al.¹⁷

Once $\Delta_{c} \left( T \right)$ has been obtained, then the full distribution function $g_{ \bot } \left( {\user2{x,K}} \right) = f + g_{ \bot }^{\left( 1 \right)} \left( {\user2{x,K}} \right)$ can be determined. In addition to f, the Fermi–Dirac equilibrium distribution function, it involves the first-order term $g_{ \bot }^{\left( 1 \right)} \left( {\user2{x,K}} \right)$ which is the solution of the Boltzmann transport equation in the relaxation time approximation. Its expression $g_{ \bot }^{\left( 1 \right)} \left( {\varvec{K}} \right) = - \tau_{ \bot } \left( { - \frac{\partial f}{{\partial \varepsilon }}} \right)\left( {\nabla F + \frac{{\varepsilon \left( {\varvec{k}} \right) - \Delta_{c} }}{T}\nabla T} \right)_{ \bot } \cdot {\varvec{\upsilon}}_{ \bot }$ involves the gradients of the absolute temperature and of the electrochemical potential F, the velocity operator ${\varvec{\upsilon}}_{ \bot }$ and the corresponding relaxation time $\tau_{ \bot }$. The expression for the transport properties can be obtained from calculations of the flow densities ${\varvec{X}}$ (of electric charge, heat and energy) in the plane perpendicular to the extrusion direction which are expressed by a scalar quantity,

$$ \left\langle {X_{ \bot } } \right\rangle = \frac{1}{V}\;\sum\limits_{{{\varvec{K}},s}} {g_{ \bot }^{\left( 1 \right)} } X_{ \bot } \left( {{\varvec{K}},s} \right)\; \approx \int_{BZ} {\frac{{d^{3} K}}{{4\pi^{3} }}g_{ \bot }^{\left( 1 \right)} X_{ \bot } \left( {\varvec{K}} \right)} $$

(A-5)

In the limit $V \to \infty$ these integrals are replaced by integrals on energy using the DOS expression (Eq. (A-4));$s$ denotes in principle other possible degrees of freedom, and here only spin degeneracy is considered.

The measured mobility is not predicted (nor experimentally observed) to be thermally activated, which means that grain boundary effects on the transport properties of these alloys can be ignored.³² This is simply a consequence of the high scattering rates due to impurities in the heavily doped samples of use for thermoelectric applications. Then the charge carriers mean free path (in the submicron scale) is much smaller than the average grain size (larger than a few micrometers).³²

As can be seeing by examining the data, intraband carrier scattering caused by absorption or emission of acoustic phonons is usually the limiting mechanism determining carrier mobility near room temperature. Hall effect data at lower temperatures will be considered, where other scattering mechanisms may play a limiting role. The expression for the scattering rate due to acoustic phonons ${1 \mathord{\left/ {\vphantom {1 {\tau_{ \bot }^{ac} }}} \right. \kern-\nulldelimiterspace} {\tau_{ \bot }^{ac} }}$ within the non-parabolic approximation has been derived in Masut et al.¹⁷:

$$ {1 \mathord{\left/ {\vphantom {1 {\tau_{ \bot }^{ac} }}} \right. \kern-\nulldelimiterspace} {\tau_{ \bot }^{ac} }} \propto T\left( {1 + 2\lambda \varepsilon } \right)^{ - 1} D\left( \varepsilon \right) $$

(A-6)

while the rate for ionized impurity scattering is given by³²:

$$ {1 \mathord{\left/ {\vphantom {1 {\tau_{ \bot }^{ii} }}} \right. \kern-\nulldelimiterspace} {\tau_{ \bot }^{ii} }} \propto {{N_{ii}^{{}} \left( {\varepsilon + \lambda \varepsilon_{{}}^{2} } \right)^{ - 1} \left( {1 + 2\lambda \varepsilon } \right)^{4} } \mathord{\left/ {\vphantom {{N_{ii}^{{}} \left( {\varepsilon + \lambda \varepsilon_{{}}^{2} } \right)^{ - 1} \left( {1 + 2\lambda \varepsilon } \right)^{4} } {D\left( \varepsilon \right)}}} \right. \kern-\nulldelimiterspace} {D\left( \varepsilon \right)}} $$

(A-7)

The physical properties in the plain perpendicular to the extrusion axis, such as the mobility, are calculated using the flows of Eq. (A-5) which involve integrals of the form $\int_{BZ} {\frac{{d^{3} K}}{{4\pi^{3} }}\tau_{ \bot } \left( {E_{c} - C} \right)^{\ell } \left( { - \frac{\partial f}{{\partial \varepsilon }}} \right)} {\varvec{\upsilon}}_{ \bot } {\varvec{\upsilon}}_{ \bot } ; \, \ell = 0,1,2...$ (C is independent of $\varepsilon$) multiplying the driving forces $\left( {\nabla F,\nabla T} \right)$. The transport coefficient will then be proportional to these integrals which can be expressed as triple-index generalized Fermi–Dirac (GFD) integrals, introduced many years ago by the work of Zawadsky et al.²³, of the form

$$ L_{k}^{n,m} \left( {\eta ,\beta } \right) \equiv \int_{0}^{\infty } {\left( { - \frac{\partial f}{{\partial z}}} \right)} z^{n} \left( {z + \beta z^{2} } \right)^{m} \left( {1 + 2\beta z} \right)^{k} dz; $$

(A-8)

where $\eta$ for electrons (holes) is $\eta_{c} \equiv {{\Delta_{c} } \mathord{\left/ {\vphantom {{\Delta_{c} } {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}} \equiv {{\left( {\zeta - E_{c0} } \right)} \mathord{\left/ {\vphantom {{\left( {\zeta - E_{c0} } \right)} {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}}$ ($\eta_{v} \equiv {{\Delta_{v} } \mathord{\left/ {\vphantom {{\Delta_{v} } {k_{B} T}}} \right. \kern-\nulldelimiterspace} {k_{B} T}}$), $\beta \equiv {{k_{B} T} \mathord{\left/ {\vphantom {{k_{B} T} {E_{g} }}} \right. \kern-\nulldelimiterspace} {E_{g} }}$, and $E_{g} \left( T \right)$ is the temperature-dependent energy gap of the semiconductor. These integrals are easy to evaluate numerically, since they contain the derivative of the equilibrium Fermi–Dirac function $\left( { - \frac{\partial f}{{\partial z}}} \right)$ which is symmetrically centered at the value $z = \eta_{c/v}$, and of narrow width for degenerate semiconductors. The expressions for the electron and hole mobilities, the electrical conductivity and the Seebeck coefficient have been given in this article and in previous publications.^17,32 Those for the Lorenz coefficient are given in this article (see "Extraction of Thermal Conductivity" section).