Introduction

Over the past decade, there has been increasing interest in shortwave infrared (SWIR) sensing and imaging in the 1.5–2.0-µm spectral band, an interest that is driven by many emerging applications in defence, space, science and industry.1,2,3,4,5 These applications have motivated a surge in competing research efforts focused on developing high-performance strained InGaAs-based photodetectors and high-performance HgCdTe IR sensors with cut-off wavelengths up to 2.7 µm, with particular emphasis on ultra-high quantum efficiency(QE).1,6,7,8,9 This demand has been further increased by requirements in both defence and space application due to the unique properties of SWIR atmospheric window.3,10

The particular interest in high-performance detectors in the extended-SWIR (eSWIR) window of the 2.0–2.7-μm wavelength band is driven by emerging applications in optical communication, long-range LIDAR, and interferometric systems based on squeezed light. These demanding applications have been made possible by recent advances in the availability of high-power rare-earth fibre lasers in this wavelength band that are eye-safe and that have favourable low-loss atmospheric transmission conditions at these wavelengths. For ease of discussion, this paper will refer to this wavelength band as 2.0 μm.

From the viewpoint of furthering fundamental science, there is an urgent need for ultra-high quantum efficiency eSWIR photodetectors for the next-generation gravitational-wave detectors of the Laser Interferometer Gravitational-Wave Observatory (LIGO): low-noise ultra-high quantum efficiency photon detectors at ~ 2.0 µm capable of operating reliably under high intensity laser illumination (~ 2 W/cm2) without loss of performance.11,12,13,14 These requirements cannot be met by existing state-of-the-art SWIR detector technology.

Utilizing commercial InGaAs material to operate in the 1.7-μm to 2-μm wavelength band poses very challenging issues which are exacerbated for wavelengths longer than 2 μm because state-of-the-art strained InGaAs devices, when compared to their lattice-matched (to InP) counterparts with a cut-off wavelength of 1.7 μm, suffer from high defect densities, lower detectivity and higher dark currents, and thus need cryogenic cooling to improve performance.15,16,17,18 Furthermore, a severe reduction of QE in extended InGaAs is observed that has been attributed to the relatively large band offsets present in heterojunction architectures that are usually employed to reduce Shockley–Read–Hall (SRH) junction dark current.19,20,21,22 While HgCdTe SWIR photodetectors have shown remarkable performance levels, the reported devices appear to be based on MWIR device designs in which the absorber composition has been tailored to the desired SWIR cut-off wavelength. Although HgCdTe devices do not face the challenge of strain-engineering, they also typically require cooling to 200 K or below. These limitations have prompted a significant increase in international research efforts to develop new material optimisation and device architecture approaches to overcome or circumvent the performance and operational limits of state-of-the-art InGaAs and HgCdTe-based eSWIR photodetector technologies.1

Figure 1 shows the QE of high-performance commercial photodetectors from different manufacturers operating in the SWIR spectral band. It is evident that all available commercial photodetectors have a QE < 80% for peak wavelengths above 2 μm corresponding to the eSWIR band and QE < 90% for wavelengths below 2.0 μm corresponding to the SWIR spectral band, which further confirms the void in the availability of ultra-high QE photodetectors at an operating wavelength around 2.0 μm. However, recently, a manufacturer in Germany has reported an InGaAs with QE ≈ 99.5% at cut-off wavelength of 1.55 μm which falls at the edge of the SWIR spectral band.23

Fig. 1
figure 1

Responsivity at peak wavelength for commercially available SWIR detectors, indicating quantum efficiencies < 80% for cut-off wavelengths greater than 2 μm. The data were collected from the website of the individual manufacturer.

Full size image

There have been several studies in the past few years on both theoretical and experimental aspects of SWIR infrared photodetectors based on the HgCdTe alloy employing p-on-n device structure.3,10,24,25,26,27,28,29,30,31 However, since these detectors were designed to be used as individual small-area pixels in an imaging array, they were not designed for ultra-high QE application. In this paper, we present the design rules which allow SWIR photodetectors operating in the eSWIR spectral range to achieve their maximum quantum efficiency.

Quantum Efficiency of SWIR HgCdTe

The detector considered in this study is a planar photodetector where the incident photons are absorbed within an absorber region and consequently generate electron–hole (e–h) pairs, and the reverse biased junction of the photodetector then collects the generated e–h pairs. The photon flux transmitted through the photodetector absorption region is shown in Fig. 2 and can analytically be expressed as:

$$ I_{1} = I_{0} e^{ - \alpha \,L} \left( {\# /{\text{cm s}}} \right) $$
(1)

where L is the thickness of the semiconductor material in cm, and α is the absorption coefficient in cm−1. The absorption coefficient α, is one of the most important parameters in determining the proportion of incident light absorbed for a given material thickness (L), something that is necessary for high QE photodiode design. For photon energies Eph greater and smaller than the reference energy ET (corresponding to the semiconductor band gap), the absorption coefficient of Hg1−xCdxTe for a range of alloy composition x, is given by:32,33

$$ E_{T} = E_{0} + \frac{{T + T_{0} }}{\sigma }\ln \frac{{\alpha_{T} }}{{\alpha_{0} }} $$
(2a)
$$ \alpha (E_{{{\text{ph}}}} ,T) = \left\{ {\begin{array}{*{20}l} {\alpha_{0} \exp \left( {\frac{{\sigma \left( {E_{{{\text{ph}}}} - E_{0} } \right)}}{{T + T_{0} }}} \right)} \hfill & {{\text{for}}\quad E_{{{\text{ph}}}} < E_{T} } \hfill \\ {\alpha_{T} \left( {\frac{2\sigma }{{T + T_{0} }}\left( {E_{{{\text{ph}}}} - E_{0} - \frac{{T + T_{0} }}{\sigma }\left( {\ln \frac{{\alpha_{T} }}{{\alpha_{0} }} - 0.5} \right)} \right)} \right)^{0.5} } \hfill & {{\text{for}}\quad E_{{{\text{ph}}}} > E_{T} } \hfill \\ \end{array} } \right. $$
(2b)
Fig. 2
figure 2

Light transmission through the semiconductor layer. I0 is the intensity of light entering the semiconductor and I1 is the intensity of light leaving the semiconductor. Absorbance is defined as the number of photons that are absorbed by the semiconductor and depends on the absorption coefficient α and the semiconductor thickness L.

Full size image

All parameters in the above model have a dependence on the Hg1−xCdxTe alloy composition (x-value). In the above equation, Eph is the incident photon energy, which can be converted to the corresponding incident photon wavelength as follows:

$$ E_{{{\text{ph}}}} = \frac{hc}{{q\lambda }} = \frac{1.24}{{\lambda \,[{\mu m}]}} $$
(3)

Using these equations, one can optimise the absorber layer thickness (L) to maximise the photon absorption. Furthermore, in order to minimize noise in photodetectors and to improve photogenerated carrier collection efficiency, it is required to minimize the thickness of the absorber layer. Doing so reduces the proportion of incident light absorbed and lowers the quantum efficiency, hence a trade-off must be made between photon absorption, electron–hole pair collection efficiency, and noise (dark current/operating temperature).34 Reducing the detector temperature results in a reduction of the dark current and, therefore, detector thermal noise, which is crucial for applications requiring long-range detection and/or in photon-starved environments. However, in this study we will only focus on the photon absorption and photocurrent parameters of the detector. The absorption coefficient allows the light absorption profile to be modelled and, therefore, assists in the development of an optimum device structure.

Figure 3a shows the absorbing layer thickness required in order to absorb 99% of the incoming photons for different values of x in Hg1−xCdxTe at T = 80 K. Changing the absorber layer x-value in turn changes the cut-off wavelength of the detector. It is evident that in order to achieve a QE > 99% at a target wavelength ~ 2.0 μm, an absorber layer with a cut-off wavelength greater than 2.5 μm is required. The thicker the absorber layer the more photons are absorbed in the absorber layer and hence a higher QE can be achieved. It should be noted that we have assumed that all absorbed photons generate an electron–hole pair and are collected by the p–n junction, which will be discussed later.

Fig. 3
figure 3

(a) The Hg1−xCdxTe absorber layer thickness required to absorb 99% of the incident photons at a particular wavelength for a range of x-values. (b) Percentage of absorbed photons for different values of absorber layer thickness when the absorber alloy composition is set to x = 0.4465.

Full size image

Figure 3b shows the absorption for different values of absorber layer thickness when the Hg1−xCdxTe alloy composition is fixed at x = 0.4465. It is evident that an absorber layer thickness of at least 3 –4 μm is required in order to absorb > 99% of the incident photons.

Figure 4 shows the absorption efficiency of the incident photons for different values of absorber layer thickness. As before, it is evident that the absorber layer must be greater than 3 μm in thickness in order to absorb more than 99% of the incoming photons.

Fig. 4
figure 4

Internal absorption of the incident photons at a particular wavelength for different values of absorber layer thicknesses (L) at T = 80 K. The Hg1−xCdxTe absorber layer alloy composition is fixed at x = 0.4465 with a corresponding λco = 2.6 μm.

Full size image

Another important parameter, which must be taken into account when designing a high QE eSWIR detector, is the x-value of mole fraction in the Hg1−xCdxTe alloy. The optimum x-value depends on a trade-off between cooling constraints and the required QE for a specific eSWIR wavelength.

Figure 5 shows the absorption efficiency versus wavelength for different values of alloy composition x in the absorber layer when the absorber layer thickness (L) is fixed at 5 μm and the operating temperature is T = 80 K. It is evident that in order to achieve the maximum absorption, the required x-value must correspond to a cut-off wavelength slightly higher than the target wavelength of operation. Therefore, in the remainder of this study, the absorber composition has been fixed at x = 0.4465, which corresponds to a cut-off wavelength of 2.6 μm and ~ 100% absorption of incident light in the 2.0 ~ 2.2-μm wavelength band for an absorber layer thickness > 3 μm.

Fig. 5
figure 5

Internal absorption of the incident photons at a particular wavelength for different values of Hg1−xCdxTe absorber layer mole-fraction x, when the absorber thicknesses (L) is fixed at 5 μm.

Full size image

Theoretical Modelling of QE and Device Design

In the previous section, the thickness of the absorber layer for maximum photon absorption was calculated analytically; however, the ultimate internal QE is a function of both the absorbed photons in the absorber layer and the collected photogenerated electron–hole pairs. Therefore, the ultimate QE calculation consists of two parts, (1) optical calculation (to extract the percentage of absorbed photons) and (2) electrical modelling to calculate the percentage of generated electron–hole pairs collected by the junction (i.e. photogenerated current). In this section, we have used the commercial device modelling software Sentaurus which couples optical and electrical models in order to design a complete photodetector structure with high QE in the eSWIR spectrum. The optical beam absorption method in Sentaurus computes optical generation by simple photon absorption using Beer’s law as explained in Sect. 2. This model is a well-established approximation and provides an accurate prediction of the photon absorption in the HgCdTe alloy.

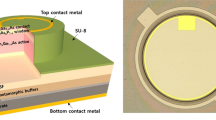
The detector considered in this section is a planar n-on-p photodiode in which the absorber layer is HgxCd1−xTe with an alloy composition chosen to be x = 0.4465, which corresponds to a cut-off wavelength of λco = 2.5 μm at the chosen elevated temperature of T = 200 K (2.6 μm at T = 80 K). The p-type absorber layer is grown by molecular beam epitaxy (MBE) and is vacancy doped, and the 0.5-μm higher-x capping layer is grown in situ. The thin n-type region can be formed by standard ion implantation or a reactive-ion etching (RIE) process.35 The detector side dimension is fixed at 50 μm, which is much larger than the absorber layer thickness L as shown in the Fig. 6. The n-type region is heavily doped with a donor doping density assumed to be ND = 5 × 1017 cm−3 and the vacancy doped p-type region has a typical acceptor doping density of NA = 5 × 1015 ~ 5 × 1016 cm−3 depending on the MBE growth parameters and post-annealing conditions, which is not a topic of this study. Nevertheless, a fixed vacancy doping of NA = 1 × 1016 cm−3 has been used in this study.24 The final doping profile after junction formation employing an RIE/implant process will have a Gaussian profile as noted in numerous publications. The n-region thickness depends on the RIE process temperature and can range from 1 μm to 3 μm.35 In this study, we use a Gaussian profile with σ = 2 μm, which corresponds to an equivalent n-type region thickness of ~ 2 μm as shown in Fig. 7. It is important to note that photon absorption can take place in the absorber layer including the RIE/implant converted region. Therefore, for the sake of consistency and in order to focus on the absorber layer properties rather than the RIE/implant region, we have kept the implant region thickness fixed and thin (less than 1 μm).

Fig. 6
figure 6

2D representation of a backside-illuminated vacancy doped n-on-p SWIR photodetector. The detector side dimension is fixed at 50 μm, and the absorber layer composition is x = 0.4465. The wider band gap capping layer has a thickness of 0.5 μm.

Full size image
Fig. 7
figure 7

Doping profile and HgxCd1−xTe alloy composition in the modelled structures. The Gaussian profile is formed using either an ion-implantation or RIE process. In this work σ = 3 μm has been chosen to provide a junction depth of 0.2 μm from the absorber/capping layer interface.

Full size image

Numerical calculations of the carrier transport were performed utilizing a drift–diffusion (DD) model available within the Sentaurus software. The two-dimensional (2D) model in this study incorporates electrical and optical material properties of HgCdTe from previously published models, and SRH, Auger and radiative recombination mechanisms in the steady-state drift–diffusion model were considered at all locations within the device.9,36,37 In the electrical model, Dirichlet boundary conditions were implemented at the ohmic contacts, where charge neutrality and equilibrium conditions are assumed. Series resistance and surface recombination effects have been assumed to be negligible and ignored in the simulations. In order to eliminate the influence of the metal contact on the minority carrier profile at the contact-absorber interface and hence dark current of the photodetector, the recombination velocity of the minority carrier has been set to zero at the metal interface.38

The quantum efficiency of a photodetector is directly related to the responsivity, which is a measure of the ratio of the output electrical signal to the input optical power. For a photovoltaic detector, the respective expression is given by:39

$$ R = \frac{{J_{{{\text{photo}}}} }}{\phi }\left( \frac{A}{W} \right) $$
(4)

where Jphoto is the photocurrent density and φ is the incident optical power density. In this study, we have assumed that monochromatic light with an intensity of 50 mW/cm2 is impinging on the photodiode surface (backside illuminated) to ensure that the detector is operating in the low-injection regime. Then, the normalized internal quantum efficiency η is calculated as a function of the incident wavelength λ, which is expressed by:

$$ \eta \left( \lambda \right) = \frac{{J_{{{\text{photo}}}} \,hc}}{\phi \lambda \,q} = R\frac{1.24}{\lambda } $$
(5)

where q is the charge, h and c are Plank’s constant and speed of light, respectively. It is worth noting that the quantum efficiency does not depend on the area.

In an ideal scenario, only Auger and radiative recombination mechanisms limit the detector QE. However, in reality, SRH lifetime plays an important role in defining the overall photodetector QE.

Figure 8 shows QE as a function of the absorber layer thickness L for an ideal planar photodetector in both n-on-p and p-on-n technologies. For a fixed value of absorber layer doping density (NA,D = 1016 cm−3), it is observed that an absorber layer thickness of ~ 3 μm (in n-on-p technology) and ~ 2.2 μm (in p-on-n technology) is required to achieve a QE > 99% at the target cut-off wavelength of 2 μm.

Fig. 8
figure 8

Internal quantum efficiency versus absorber layer thickness for different values of SRH lifetime at a target wavelength of ~ 2.0 μm and T = 200 K with ND,A = 1016 cm−3 for both n-on-p and p-on-n photodetector technologies. The reported experimental values of SRH lifetime are typically in the range of ~ 20 ns for p-type vacancy doped material and ~ 1 μs for n-type In-doped absorber layers.

Full size image

It can also be observed that the QE strongly depends on the SRH lifetime of the minority carriers. The minority carrier lifetime in p-type vacancy doped LPE grown absorber for eSWIR band has not been widely reported in the literature; however, recent experimental results on MBE grown material suggest a value in the range of ~ 20 ns.40 On the other hand, the reported SRH lifetime in In-doped, MBE grown n-type absorber layers is in the order of ~ 1 μs.40,41,42,43 The direct experimental comparison of n-on-p and p-on-n photodetectors operating in the eSWIR band with cut-off wavelength of 2 μm has been undertaken by CEA-LETI in France on a vacancy doped p-type absorber (grown by LPE) and on In-doped n-type absorber (grown by MBE). The results show a similar quantum efficiency for both technologies. However, both technologies demonstrated a higher dark current density compared to the Rule07 values reported by Teledyne, which implies that the n-type MBE grown absorber layer from Teledyne has a much higher SRH lifetime compared to the CEA-LETI grown material.

In a realistic photodetector device, the maximum achievable QE is determined by the absorber layer thickness and SRH lifetime, the latter being directly related to the absorber material quality, and therefore, knowing the minimum required SRH lifetime in different scenarios can assist in a better detector design.

Figure 9 shows the responsivity and QE as function of the absorber layer thickness for both n-on-p and p-on-n technologies. For the p-type absorber, the SRH lifetime is fixed at 20 ns, which corresponds to the reported value in vacancy doped layer with average doping density of 1 × 1016 cm−3 achievable in experiment.24,44 Considering a moderate SRH lifetime of ~ 1 μs, the calculated QE in MBE grown n-type layer is very sensitive absorber layer thickness. That is why all the reported backside-illuminated, MBE-grown p-on-n eSWIR detectors have been designed with an absorber layer thickness of 3–4 μm in order to achieve the maximum QE while minimising the impact from the SRH lifetime.24,43

Fig. 9
figure 9

Internal quantum efficiency as a function of the absorber layer thickness L for n-on-p and p-on-n eSWIR photodetectors with a fixed SRH lifetime of 20 ns (vacancy doped n-on-p absorber) and 1 μs (p-on-n In-doped absorber) at T = 200 K. Increasing the absorber layer thickness initially increases the QE due to an increase in the absorption of incoming photons. However, continuing to increase the absorber layer thickness beyond ~ 3 μm leads to a reduction in QE since it is the minority carrier diffusion length that determines the optimum absorber layer thickness, which is ~ 3 μm.

Full size image

Figure 10a shows the influence absorber layer doping density on the QE for different values of SRH lifetime in p-type absorber layer. It is evident that the QE does not change significantly for the doping density in range of ~ 1016 cm−3 which is a routinely achievable value in the vacancy doped p-type layer.44,45 Figure 10b shows the QE versus doping density for n-type absorber layer. It can be observed that for a 3-μm thickness, a minimum SRH lifetime of > 1 μs is required to achieve a high QE. As mentioned previously, moderate ~ 1 μs SRH lifetime can be achieved routinely in MBE grown n-type In-doped absorber layer.

Fig. 10
figure 10

Internal quantum efficiency as a function of the absorber layer doping concentration for n-on-p and p-on-n technologies operating in the eSWIR band. A long SRH lifetime can be achieved in the In-doped n-type absorber layer, whereas it is difficult to achieve a minority carrier lifetime of more than 50 ns in the vacancy doped p-type absorber layer.

Full size image

Figure 11 shows the best reported QE values for infrared focal plane arrays operating in the SWIR band for the space application by Teledyne in the USA and Sofradir in France at an operating temperature of T = 90 K.46 Epitaxial growth and detector structure are summarized in Table I. Sofradir has reported two identical SWIR FPA grown by MBE (p-on-n technology) and LPE (n-on-p technology). The absorber layer thickness reported by Sofradir is on the order of 4–6 μm for both growth methods, and Teledyne has not provided any data on device structure. It is clear that there is not a significant difference in quantum efficiency between MBE grown p–n and LPE grown n–p detectors as predicted by theoretical calculations. However, the (HAWAII-2RG) SWIR FPA grown by MBE (p-on-n structure) and reported by Teledyne demonstrates slightly higher QE compared to the Sofradir technology. According to our calculation, this difference may be due to utilization of a better engineering trade-off between the diffusion length (lifetime/mobility-dependent) and absorber layer thickness of the Teledyne’s detector. The FPAs reported are backside illuminated and in order to minimise the reflection, all of the FPAs have substrate thinned and are finished with an anti-reflective coating (ARC). For example, LETI employs a monolayer quatrawave ARC as part of the standard processes of detector manufacturing, which results in a 30% increase in QE, and provides less than 5% reflectivity in the 0.7 to 2.5 spectral band.46,47,48

Fig. 11
figure 11

Comparison of reported quantum efficiency in high-performance eSWIR Hg1−xCdxTe FPAs at T = 90 K. It is evident that a vacancy doped n-on-p technology has a comparable QE to p-on-n In-doped MBE grown technology. However, the QE reported by LETI is marginally lower than the values reported for the Teledyne (HAWAII-2RG) FPA. The QE values have been taken from literature.46

Full size image

High Injection Effects in HgCdTe SWIR Detectors

For infrared sensing and imaging applications, it is usually assumed that the photodetector operates in the low-injection regime where the density of photogenerated carriers is much lower than the equilibrium density of the majority carriers in the absorber layer. However, for specific applications (laser detection) where the intensity of the incoming light is so high that the photogenerated carrier density becomes comparable and even larger than the equilibrium majority carrier density, a detector operates in the high injection regime and, therefore, requires a completely different design of absorber layer. The SWIR detectors in the LIGO gravitational wave detectors are an example of such high-power applications where the photodetector is under illumination by SWIR laser with incident power on the order of 50 W/cm2. One way of improving the detector performance under such conditions is to reduce the doping density in the absorber layer and allow the photodetector to operate in the fully depleted mode, which can significantly reduce the recombination mechanism and, therefore, increase in the QE and performance of the detector. Achieving such low doping densities in the absorber layer is only possible via the extrinsic n-type doping of the absorber (because no such low level in vacancy doped or extrinsic p-type material has been reported). Therefore, in this section, we consider a p-on-n photodetector technology with a fixed SRH lifetime of 1 μs and n-type absorber layer of 3 μm which is consistent with previous calculations.

In the case of a p-type absorber, we consider a fixed acceptor doping density of 1 × 1016 cm−3 which is the nominal value for a vacancy doped p-type absorber layer and can be achieved experimentally, as reported in the literature. The detector schematic and carrier densities in the high-injection and low-injection regimes are shown in Fig. 12. It can be seen that for incident power densities higher than 1 W/cm2 , the detector enters the high-injection regime.

Fig. 12
figure 12

Minority carrier density in a photodetector for different values of incident power density (Pin). By increasing the incident power density, the photogenerated minority carrier density becomes comparable to the majority carrier density. Eventually, for very high power densities (greater than ~ 1 W/cm2), photogenerated minority carrier density exceeds the donor doping concentration.

Full size image

In order to assess the influence of high-injection effects on the QE of eSWIR photodetector, the QE has been calculated numerically for the low-injection regime (incident power of Pin = 50 mW/cm2) and the high-injection regime (incident power of Pin = 100 W/cm2). We include all the SRH, Auger and radiative recombination mechanisms as before. In order to provide a set of design rules for high QE photodetector under high power, we considered a broad range of doping density and incident power at temperature of T = 200 K (Table I).

Table I Comparsion of high QE SWIR FPA
Full size table

Figure 13 shows the QE of the p-on-n photodetector as a function of doping density and incident power density for a fixed value of SRH lifetime and absorber thickness. It is evident that a at high-injection regime, the QE degrades significantly due to an increase in the recombination rate of the Auger mechanism. However, decreasing absorber layer doping density levels can improve the QE by increasing the depletion region and suppressing the Auger mechanism. Figure 14 shows QE versus absorber layer thickness for different values of SRH lifetime. In the calculations, the incident power density is fixed at 100 W/cm2 and the doping density is fixed at NA = 1016 cm−3 which is equal to experimentally achievable values by LPE and MBE growth methods. As expected, increasing the SRH lifetime and decreasing the absorber layer thickness can assist with reaching 90% QE in the high-injection regime. The CEA-LETI in France has reported an eSWIR FPA for imaging application with an absorber doping density of 1016 cm−3 in n-on-p technology employing vacancy doped LPE grown material, however, the chosen absorber layer thickness of 7 μm is not suitable for high-power/high-QE sensing applications.24

Fig. 13
figure 13

QE versus absorber layer doping density in p-on-n photodetector technology with different values of incident power density. Increasing the incident power density above ~ 1 W/cm2 will result in a photogenerated minority carrier density comparable to the majority carrier density and, therefore, degradation of the detector QE.

Full size image
Fig. 14
figure 14

QE versus absorber layer thickness in n-on-p photodetector technology with different values of SRH lifetime. The absorber layer doping density equals 1016 cm−3 which is a typical value for a vacancy doped material. It is evident that in the presence of a high incident power density of 100 W/cm2 and moderate SRH of 20 nm, the n-on-p technology can still offer an ultra-high QE due to long diffusion length of minority carriers.

Full size image

Conclusion

We presented the design criteria for an ultra-high quantum efficiency (QE > 99%) SWIR photodetector employing a HgCdTe alloy for sensing applications in both n-on-p and p-on-n technologies. Numerical and analytical models were used to study the SWIR detector performance and it was demonstrated that ultra-high QE > 99% can be achieved in the vacancy doped n-on-p photodetector technology due to long diffusion length of the minority carriers and similarly in low-doped p-on-n technology with ND < 1014 cm−3. Furthermore, for the application with high incident power (power greater than 1 W/cm2), the detector enters the high injection regime and high recombination rates require vacancy doped LPE grown n-on-p with short absorber layer or the detector with p-on-n technology where low n-type doping is technologically achievable.