Impact of Substrates on the Electronic and Mechanical Properties of Al_xIn_1−xP_ySb_1−y Alloys

Abstract

The compositional dependence of electronic and mechanical properties of a Al_xIn_1−xP_ySb_1−y quaternary alloy in zinc-blende structure lattice-matched to GaSb, InAs, and InP substrates is studied. The calculations are done based on the empirical pseudopotential method modified with virtual crystal approximation. Our calculations are obtained for the energy band gaps, elastic constants, elastic moduli, bond stretching, bond bending forces, and internal strain parameter. The material system of interest is found to be a direct semiconductor within a small range of Al concentrations about 0–0.07 and an indirect one outside this region. The Debye temperature and the Fröhlich coupling constant have been determined at different values of composition lattice-matched to different substrates. The phonon frequencies and the sound velocity for different substrates at various compositions have been studied. There is a good agreement between our results and the experimental data for its constituent binary compounds, AlP, AlSb, InP, InSb, and ternary alloys, InPSb, AlPSb, which supports the calculated results of the studied Al_xIn_1−xP_ySb_1−y quaternary alloy. The studied properties for the considered alloy may be helpful for the fabrication of optoelectronic devices.

Introduction

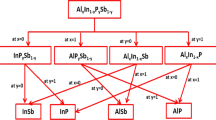
Semiconductors consisting of the third and fifth group elements of the periodic table are the key materials for optoelectronic devices. Al_xIn_1−xP_ySb_1−y quaternary alloys are important materials and have important technological device applications.¹ x and y are the concentrations of Al and P in the considered alloy, respectively. One advantage of the Al_xIn_1−xP_ySb_1−y alloy is that it can be grown lattice-matched to binary substrates, GaSb, InAs, and InP. Special attention has been given to the mechanical properties of semiconductors because they are one of the best tools for guiding the successful design and fabrication of optoelectronic devices.^1,2,3,4,5,6 This work aims to focus on the effect of the used substrates (GaSb, InAs, and InP) on the electronic and mechanical properties in Al_xIn_1−xP_ySb_1−y under the effect of alloy composition. The studied quaternary alloy is bordered by the ternary alloys, Al_xIn_1−xP, Al_xIn_1−xSb, AlP_xSb_1−x, and InP_xSb_1−x , which are bounded also by four binary compounds, AlP, AlSb, InP, and InSb. These binary compounds and ternary alloys were studied by Degheidy et. al. and have been published in Refs. 7,8,9,10 The structural, electronic, mechanical, thermal, and optical properties of ternary and quaternary semiconductor alloys were investigated using different methods such as first-principles plane-wave method within the LDA approximations, EPM, and density functional theory (DFT).^{9,10,11,12,13,14,15,16,17,18,19,20,21}

In the present work, the direct and indirect energy band gaps, the elastic constants (C₁₁, C₁₂, C₄₄), elastic moduli (B_u, C_s, Y₀), and some related properties such as bond stretching (α), bond-bending (β) force constants and internal strain parameter (ξ) of Al_xIn_1−xP_ySb_1−y lattice-matched to different substrates have been studied. Our calculations are based on the empirical pseudopotential method (EPM) modified with virtual crystal approximation (VCA).^22,23 Our results over the compositional range of Al concentration (x=0–1) in the Al_xIn_1−xP_ySb_1−y system are performed and compared with the published data in the literature and showed good agreement especially for binary compounds and ternary alloys which supports the results of the quaternary alloy of interest.

Computational Method

The present calculations were performed by using the empirical pseudopotential method (EPM) combined with the virtual crystal approximation (VCA).^{8,9,22,23,24,25,26,27,28,29,30,31}

The fundamental benefit of employing pseudopotentials is that only valence electrons must be taken into account. The electrons in the core are handled as though they were frozen in an atomic-like state. The valence electrons are assumed to move in a weak one-electron potential as a result of this. Model pseudopotentials are substituted for actual pseudopotentials to further simplify the problem. Even though there are alternative methods for estimating electronic band structures, the pseudopotential method produces surprisingly accurate results for the amount of computer time and effort required. The EPM involves empirical parameters, namely the symmetric and anti-symmetric form factors which are modified to fit the experimental energy band gaps of the parent binary compounds of the studied alloy, namely AlP, AlSb, InP, and InSb.³² The obtained accurate form factors results allow us to calculate the form factors of the quaternary Al_xIn_1-xP_y Sb_1-y alloy of interest, where

$$ W_{{{\text{alloy}}}} (x) = xy \, W_{AlP} + y(1 - x) \, W_{InP} + x(1 - y) \, W_{AlSb} + (1 - x)(1 - y) \, W_{InSb} $$

(1)

The lattice constant of the Al_xIn_1-xP_y Sb_1-y alloy can be also determined in terms of those of lattice constants of the constituent binary compounds $a_{AlP}$, $a_{InP}$, $a_{AlSb}$ and $a_{InSb}$ using Vegard's law³³ as

$$ a_{alloy} = xya_{AlP} + y(1 - x)a_{InP} + x(1 - y)a_{AlSb} + (1 - x)(1 - y)a_{InSb} $$

(2)

The Lyddane–Sachs–Teller relation were used to determine the longitudinal and transverse phonon frequencies (LO and TO).^34,35

$$ \frac{{{\upomega }_{{{\text{TO}}}}^{2} }}{{{\upomega }_{{{\text{LO}}}}^{2} }} = \frac{{{\upvarepsilon }_{\infty } }}{{{\upvarepsilon }_{{\text{o}}} }}{ } $$

(3)

$$ \omega_{LO}^{2} - \omega_{TO}^{2} = \frac{{4\pi e_{T}^{*2} e^{2} }}{{M\Omega_{o} \varepsilon_{\infty } }} $$

(4)

where ε_∞, ε₀, e_T*, e, M, Ω are the high-frequency dielectric constant, static dielectric constant, transverse effective charge, electron charge, twice the reduced mass, and volume occupied one atom, respectively.

The sound velocity was calculated using the crystal density (g) and stiffness constants (c_ij).³⁶

$$ {\text{v}} = \sqrt {\frac{{{\text{c}}_{{{\text{ij}}}} }}{{\text{g}}}} $$

(5)

If the quaternary alloy of interest is lattice-matched to a substrate, namely GaSb, InAs, InP, the lattice matching condition is obtained by using the lattice constant of a substrate instead of the lattice constant of the studied alloy. The substrate lattice matching relations are given by

For GaSb substrate³⁶

$$ {\text{y = }}\frac{{{0}{{.3835 - 0}}{\text{.3439 x}}}}{{{0}{\text{.6104 + 0}}{\text{.0616 x}}}},\;{0} \le {\text{x}} \le 1 $$

(6)

For InP substrate³⁶

$$ {\text{y = }}\frac{{{0}{{.6104 - 0}}{\text{.3439 x}}}}{{{0}{\text{.6104 + 0}}{\text{.0616 x}}}},\;{0} \le {\text{x}} \le 1 $$

(7)

For InAs substrate³⁶

$$ {\text{y = }}\frac{{{0}{{.4211 - 0}}{\text{.3439 x}}}}{{{0}{\text{.6104 + 0}}{\text{.0616 x}}}},\;{0} \le {\text{x}} \le 1 $$

(8)

Or in general,

$$ {\text{x = }}\frac{{d_{1} + d_{2} y}}{{d_{3} + d_{4} y}}{ , 0} \le {\text{x}} \le 1 $$

(9)

where di are expressed in terms of the corresponding lattice constants of the binary compounds, where

$$ {\text{d}}_{{1}} {\text{ = a}}_{{{\text{sub}}}} -{\text{ a}}_{{{\text{InSb}}}} \, $$

(10)

$$ {\text{d}}_{{2}} {\text{ = a}}_{{{\text{InSb}}}} -{\text{ a}}_{{{\text{InP}}}} \, $$

(11)

$$ {\text{d}}_{{3}} {\text{ = a}}_{{{\text{AlSb}}}}- {\text{ a}}_{{{\text{InSb}}}} \, $$

(12)

$$ {\text{d}}_{{4}} {\text{ = a}}_{{{\text{AlP}}}} {\text{ + a}}_{{{\text{InSb}}}} {{ - \text{(a}}}_{{{\text{InP}}}} {\text{ + a}}_{{{\text{AlSb}}}} {)} $$

(13)

Knowing the form factors and the lattice constants of the Al_xIn_1−xP_ySb_1−y system for a certain composition parameter x, the energy eigenvalues are calculated by solving numerically the secular determinant, more details are found in^37,38

$$ \left\| {\frac{1}{2}\left| {\vec{k} + \left. {\vec{G}^{^{\prime}} } \right|} \right.^{2} - } \right.\left. {E(x)_{nk} + \sum\limits_{{\vec{G} \ne \vec{G}^{\prime}}} {V(x,\left| {\Delta \vec{G})} \right.} } \right\| = 0\,\,\,\,\, $$

(14)

The band structure calculation in this method is designed to solve the eigenvalue problem for the energy E, as indicated by Eq. 14. V(G') is the Fourier component of the periodic part of the Bloch function, as seen in Eq. 14. The size of the matrix and the precision of the calculation are both determined by the number of employed reciprocal lattice vectors. A specimen of length 50a is used to select $\vec{k}(\vec{k}_{x} ,\vec{k}_{y} ,\vec{k}_{z} )$ values, where the number of sample points is twice the value of 50, i.e. 100, by taking into account the entire Brillouin zone (BZ) interval [−1, 1]. x is calculated for the energy band gaps for the binary compounds, AlP, AlSb, InP, and InSb, and some of their related alloys lattice-matched to GaSb, InAs, and InP for some Al concentrations and compared with the available published data.

Results and Discussion

In Table I, we give our results for the calculated direct $E_{g}^{\Gamma } (x)$, and indirect $E_{g}^{L} (x)$,$E_{g}^{X} (x)$ energy band gaps of Al_xIn_1−xP_ySb_1−y lattice-matched to GaSb, InAs, and InP substrates for the compositional parameter, x. Some results are compared with the available theoretical or experimental data from the literature^{1,8,9,36,39,40,41} and showed good agreement. It is known that the lattice constant of InP is less than that of InAs and GaSb. Because the energy band gaps and the lattice constant have an inverse relationship in this scenario, the energy band gaps of the quaternary alloy lattice-matched to InP are larger than those lattice-matched to GaSb and InAs substrates over the entire composition region.

Table I Band-gap energies of AlP, AlSb, InP, InSb and their alloys lattice-matched to different substrates for some compositions (x) at room temperature and normal pressure

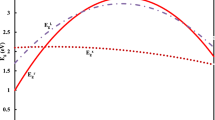
The variation of the direct energy band gaps $E_{g}^{\Gamma }$ of Al_xIn_1−xP_y Sb_1−y alloy versus its Al content for the three different substrates is displayed in Fig. 1. In this figure, we observe that ${\mathrm{E}}_{\mathrm{g}}^{\mathrm{\Gamma}}$ are increased with increasing the composition parameter x in the region 0–0.3 and then slightly decreased whatever substrate was used. The energy band gaps of Al_xIn_1−xP_y Sb_1−y lattice-matched to InP have larger values than those lattice-matched to GaSb and InAs substrates. However, the variation of ${\text{E}}_{{\text{g}}}^{\Gamma }$band gap of Al_xIn_1−xP_ySb_1−y lattice-matched to GaSb and InAs substrates is very close.

Fig. 1

The energy band gap E_g^Γof Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition (x).

Table II shows our results for the polarity and the transverse effective charge of Al_xIn_1−xP_y Sb_1−y lattice-matched to GaSb, InAs, and InP substrates. For comparison, available published data are presented and a good agreement is reported. With increasing Al concentration, x, the polarity of Al_xIn_1−xP_y Sb_1−y is slightly decreased for all used substrates. The transverse effective charge has the same behavior of the polarity and their values are larger when the alloy is lattice-matched to InP compared to GaSb and InAs substrates.

Table II Polarity(${\alpha }_{p}$) and transverse effective charge $\left({e}_{T}^{*}\right)$ of AlP, AlSb, InP, InSb, and their alloys lattice-matched to different substrates for some compositions (x) at room temperature and normal pressure

The calculated elastic constants C₁₁, C_12, and C₄₄ of Al_xIn_1−xP_y Sb_1−y for some different values of Al concentration and all substrates are listed in Table III and displayed in Fig. 2. From the results, it is seen that all the elastic constants are slightly increased when Al content is enhanced whatever the used substrates. The trends of the elastic constant of the alloy when using GaSb, InAs and InP substrates are qualitatively consistent with each other. Further quantitative analysis shows that the largest elastic constant is obtained when alloy is lattice-matched to InP substrate while the smallest elastic constant is obtained when the alloy is lattice-matched to GaSb in the entire composition range. This is because the polarity of InP is higher than that of InAs and GaSb. Also, InP has a smaller nearest-neighbor distance than GaSb and InAs. The elastic constants C₁₁, C₁₂, and C₄₄ are inversely proportional to the nearest-neighbor distance and are directly proportional to polarity. For all substrates, the values of C₁₁ are larger than C₁₂ and C₄₄ values. Our results are compared with the available published data and showed good agreement. In Table III, the values of the elastic factors fulfill the stability conditions C₁₁>0, C44>0, C₁₁–C₁₂>0, C₁₁+2C₁₂>0,⁴⁶ which shows that Al_xIn_1-xP_y Sb_1-y alloys are mechanically stable in their structure.

Table III Elastic constants of AlP, AlSb, InP, InSb and their alloys lattice-matched to different substrates for some compositions (x) at room temperature and normal pressure

Fig. 2

Elastic constants (C₁₁, C₂, C₄₄) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition (x).

In Table IV, we show our results for the bulk $B_{u}$, shear $C_{s}$, and Young $Y_{o}$ moduli in Al_xIn_1−xP_y Sb_1−y lattice-matched to GaSb, InAs, InP substrates fot some compositions (x). The trends of the elastic parameters with enhanced Al content in Al_xIn_1−xP_ySb_1−y are qualitatively similar for all used substrates. The bulk, Young's and shear moduli have the same behavior for the elastic constants. This is because they depend on the elastic constants C₁₁, C₁₂, and C₄₄. Their values are slightly increased with increasing x; however, the real values for InP substrate are larger than those for other substrates. The variation of $B_{u}$ $C_{s}$ and $Y_{o}$ moduli versus x are displayed in Fig. 3. According to Pugh's correlation,⁴⁹ the Al_xIn_1−xP_y Sb_1−y alloys are ductile materials. This is because the calculated bulk/shear values for the alloys under investigation are greater than 1.75.

Table IV Elastic moduli of AlP, AlSb, InP, InSb and their alloys lattice-matched to different substrates for some compositions ( x) at room temperature and normal pressure

Fig. 3

Elastic moduli (Y_o, C_s, B_u) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition (x).

The bond-stretching $(\alpha )\,$, bond-bending $(\beta )\,$ force constants, and internal strain parameters $(\zeta )$ for some compositional alloys and the different substrates are inserted in Table V and displayed in Fig. 4. Our results in this table are compared with the existing data in the literature and a good agreement is observed. From Fig. 4, we show that $(\alpha )\,$ and $(\beta )\,$ are slightly increased with increasing Al concentration; however, $\zeta$ has the smallest values and is not affected by enhancing the compositional parameter whatever the used substrates.

Table V Calculated bond-stretching (α), bond-bending (β) force constants, and internal strain parameter (ζ), of AlP, AlSb, InP, InSb, and their alloys lattice-matched to different substrates for some compositions (x) at room temperature and normal pressure

Fig. 4

bond-stretching (α), bond-bending (β) force constants and internal strain parameter (ζ) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs, and InP substrates as a function of composition (x).

The LO phonon frequency's Debye temperature is a significant parameter in the research of polaron mobility at finite temperatures. This temperature is given by $\theta_{D} = \frac{{\hbar \omega_{Lo} }}{k}$, where $k$ is the Boltzmann’s constant. The Debye temperature (θ_D) for the Al_xIn_1−xP_ySb_1−y alloy for different substrates (GaSb, InAs, and InP) as a function of composition (x) is displayed in Fig. 5. It is seen that the Debye temperature is increased nonlinearly by increasing composition. Also, the Debye temperature for the Al_xIn_1−xP_ySb_1−y alloy lattice-matched to the InP substrate has higher values than the InAs and GaSb substrates.

Fig. 5

Debye temperature (θ_D) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition (x).

The LO and TO phonon frequencies are determined by the Lyddane–Sachs–Teller relation.^34,35 The calculated LO(Γ) and TO(Γ) phonon frequencies and their dependence on composition for Al_xIn_1−xP_ySb_1−y alloy at different substrates are shown in Fig. 6. As observed in our results, the frequencies of these two modes increases non-linearly with increasing composition from 0 to 1. Subsequently, the transverse effective charge is increased with increasing composition, since the transverse effective charge increases with the composition. The stronger the bond level, the higher the vibration frequency, and vice versa. The optical phonon mode, which is dependent on the bond level, has the maximum vibrational frequency at the Г-point. The phonon frequencies (ω_LO, ω_TO) in 10¹³ s⁻¹ of the central optical phonon modes for AlP, AlSb, InP, and InSb compounds were calculated to be (11.25, 9.98), (8.87, 8.53), (6.81, 6.19), and (3.22, 3.03), respectively. It is noted that the calculated values of ω_Lo and ω_To are in reasonable agreement with the experimental and published data,^22,44,53,54 justifying the reliability of our calculated data. The obtained data for the calculated longitudinal and transverse phonon frequencies of Al_xIn_1−xP_ySb_1−y at different values of composition may be taken as a reference for future experimental work. It is observed that the Al_xIn_1−xP_ySb_{1−y alloy has higher values of the phonon frequencies} ω_Lo and ω_To for the InP substrate than the other two substrates (GaSb and InAs).

Fig. 6

Phonon frequencies (ω_LO and ω_TO) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs, and InP substrates as a function of composition (x).

It is well recognized that studying transport and optical properties in polar semiconductors necessitates an understanding of the electron-LO lattice vibration coupling, which cannot be overlooked. The well-known Fröhlich coupling constant is a measure of the interaction between electrons and LO phonons which is given by $\alpha_{F} = 0.5\left( {\frac{1}{{\varepsilon_{\infty } }} - \frac{1}{{\varepsilon_{0} }}} \right)\frac{{e^{2} /\left( {\hbar /2m*\omega_{Lo} } \right)^{0.5} }}{{\hbar \omega_{Lo} }}$, ^55,56 where m* is the electron effective mass. It is highly influenced by the crystal's ionic polarization, which is linked to the dielectric constants. Figure 7 shows Fröhlich coupling constant (α_F) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition, which shows that it increases with increasing composition from 0 to 0.25 and decreases from 0.25 to 1 for two substrates (GaSb and InAs). It is noted that this constant increases by increasing composition from 0 to 0.4 and decreases from 0.4 to 1 for the InP substrate. The constant has higher values for the InP substrate than the other two substrates.

Fig. 7

Fröhlich coupling constant (α_F) of Al_xIn_1−xP_ySb_1−y for GaSb, InAs and InP substrates as a function of composition (x).

The longitudinal and transverse sound velocity propagating along with the three major directions [100], [110], and [111] for the Al_xIn_1−xP_ySb_1−y alloy for different values of composition and different substrates are listed in Table VI and displayed in Fig. 8a, b, and c. The calculated data of the sound velocity (in 10⁵ cm/s) along the three major directions for the considered alloys are in good agreement with the available results (in Table VI). The calculated results of the sound velocity at the rest values of composition may be taken as a reference for future experimental work. It can be observed from Fig. 8 that the longitudinal and transverse sound velocity for the three major directions [100], [110], [111] of Al_xIn_1−xP_ySb_1−y is increased with increasing composition. It is noted that the acoustic velocity for Al_xIn_1−xP_ySb_1−y lattice-matched to InP substrate has higher values than that for InAs and GaSb substrates.

Table VI Sound velocity propagating along with the three major directions [100], [110] and [111] of AlP, AlSb, InP, InSb and their alloys lattice-matched to different substrates for some compositions (x) (in 10⁵cm/s) at room temperature and normal pressure

Fig. 8

The acoustic velocities of Al_xIn_1−xP_ySb_1−y for (a) GaSb substrate, (b) InAs substrate, and (c) InP substrate as a function of composition (x).

Conclusion

Based on EPM within the virtual crystal approximation (VCA), the energy band gaps of Al_xIn_1−xP_ySb_1−y lattice-matched to GaSb, InAs, and InP substrates and its constituents are calculated for different Al concentrations. The polarities and transverse effective charge of the Al_xIn_1−xP_ySb_1−y system are determined from the symmetric and anti-symmetric form factors at G(1,1,1) using Vogl's definition. The elastic constants C₁₁, C₁₂, C_44, and their related elastic moduli ${\mathrm{B}}_{\mathrm{u}}$, ${\mathrm{C}}_{\mathrm{s}}$ and ${\mathrm{Y}}_{0}$ are calculated and their variation with Al concentration has been examined. Also, the bond-stretching $(\alpha )\,$, bond-bending $(\beta )\,$ force constants, and internal strain parameters $(\zeta )$ are calculated for the used substrates. The Debye temperature and the Fröhlich coupling constant have been determined at different values of composition lattice-matched to different substrates. The phonon frequencies and the sound velocity for different substrates at various compositions have been studied. Most of our results are compared with the known data in the literature and showed good agreement. Our data cover a wide range accessed by varying compositions and substrates. The calculated quantities in this work may be of great interest for both theoretical experimental research and devise applications; it opens up the possibility of developing new electronic devices.