Interplay Between Electronic States and Structural Stability in Cation-Deficient VCoSb, NbCoSb, and TaCoSb Half-Heuslers

Abstract

The effects of the vacancy concentration at the cation site of three half-Heuslers, VCoSb, NbCoSb, and TaCoSb, were studied with a combination of two computational methods: density functional theory and Monte Carlo simulations, both linked by a cluster expansion method. Our density functional method allows us to follow a gap opening in the electronic density of states in NbCoSb and TaCoSb as a function of vacancy concentration, starting from a metallic state with the Fermi-level crossing the valence states in the pristine crystal, passing throughout a p-type doped behavior, down to a semiconducting state at 20% of vacancies. In the case of VCoSb, the transition starts from the half-metallic ferromagnetic state, where VCoSb remains half-metallic until it achieves a semiconductor state at V$_{0.8}$CoSb composition, the transition leading to a magnetic–nonmagnetic crossover. Further increase of vacancies leads to non-polarized in-gap states in V$_{0.75}$CoSb, and polarized in-gaps in Nb$_{0.77}$CoSb, while Ta$_{0.75}$CoSb recovers a metallic behavior but with an n-character. Based on our cluster expansion, we can assert that Ta$_{0.8}$CoSb is slightly more stable than Nb$_{0.8}$CoSb, while both are much more stable than V$_{0.8}$CoSb. Temperature effects were studied through Monte Carlo simulations. The simulations show that, upon cooling, the ground states are hard to recover, and instead metastable states are formed. The vacancy arrangements were scrutinized with the help of suitable order parameters for the lattice vacancy occupation.

Introduction

Point defects may appear spontaneously during the manufacturing of a material,¹ and, despite its misleading name, they are sometimes quite desirable in many branches of material science. When targeting specific physical properties, controlled and selectively induced defects can be used for introducing or tuning desired physical properties.² For instance, point defects play a key role in the field of transparent semiconductors and,^3,4,5 recently, it was proposed that vacancies could provide an alternative to obtain the long sought-after p-type transparent semiconductor.⁶ In half-Heusler (HH) thermoelectrics, based on semiconductor materials, the understanding and judicious selection of defects has also been beneficial to the performance of materials.^7,8,9,10

In thermoelectric materials, the presence of vacancy defects can help to tune the power factor or/and the lattice thermal conductivity to deliver a higher figure-of-merit (ZT). Thus, one finds reports of vacancies assisting the desired reduction of the lattice thermal conductivity in CuGaTe$_{2}$,¹¹ while in SnTe-In$_{2}$Te$_{3}$,¹² Ge$_{9}$Sb$_{2}$Te$_{12}$,¹³ and $\beta$-Zn$_{4}$Sb$_{3}$,¹⁰ the presence of vacancies simultaneously improves the electrical properties and reduces the lattice thermal conductivity. In these improved thermoelectric examples, as in most cases in the field of thermoelectricity, the target was materials with good semiconducting behavior. What we will discuss in this paper is a different strategy in the use of vacancies to control electronic properties in materials, particularly within the family of HH. We present a way to turn a metal (semi-metal) into a semiconductor as well as the possibility of inducing intrinsic n- or p-doping via vacancies.

The idea has prevailed that one should first select those HHs which meet 18-valence electron count (VEC) criteria,^{14,15,16,17,18,19,20,21,22} and then improve their electronic and phonon characteristics. This approach has shown to be useful in HH intermetallic compounds, which are among the thermoelectric material classes that have steadily improved their ZT, already achieving values of 1.5.²³ However, this view was challenged following ZT measurements in 19 VEC HH at 973 K with ZT = 0.4 for NbCoSb²⁴ and ZT = 0.5 for the Nb$_{0.44}$V$_{0.44}$Ta$_{0.12}$ CoSb alloy.²⁵ A remarkable discovery²⁶ in cation-defective HH increased ZT to 0.9 at 1123 K in Nb$_{0.83}$CoSb. In these new materials, their hallmark is the structural stability found at near 20% of vacancy concentration and optimal ZT slightly above this concentration^27,28 with the presence of a semiconducting gap. To explain this emergent feature, one should think of NbCoSb as a heavily doped semiconductor, rather than as a metal.²⁹ Based on these observations, a modification of the 18-VEC rule seems more appropriate to predict the formation of stability in a broader range of HH composition, which includes defects.³⁰ The new criterion uses the valence band electronic configuration, which should amount to zero to achieve a semiconductor phase. This novel formulation opens the opportunity to a new route to obtain a semiconductor phase via the manipulation not only of vacancies but also of interstitial and substitutional defects.

On the other hand, cluster expansion (CE) methods have played a very decisive role in computationally corroborating the structural stability at near 20% of vacancy concentration.^26,27,31 The aforementioned work showed that CE can handle very well a considerable amount of defects in HH. More recently,³² and quite remarkably, Monte Carlo methods based on very simplified models of interaction have been able to reproduce some of the distinctive features seen in electron diffraction patterns of defective HH systems.

In the light of these discoveries, we decided to scrutinize three 19-VEC HH within a range of vacancy concentrations (x) which simultaneously stabilize the materials and tune their electronic transport properties. We investigate three isoelectronic HH with formula M$_{1-{\mathrm{x}}}$CoSb (M = V, Co, Sb). For that, we employ a CE which has previously been successfully applied to HHs.^7,33,34 First, we will detail the transition from a metallic state to semiconductor states triggered by the introduction of vacancies at the M site. We show that the vacancy concentration regulates the transition and makes the materials behave effectively as a doped semiconductor, with the possible ability to set an n or p character for concentrations slightly below or above x = 0.2, respectively. In the second part, we show how the vacancies self-organize in a particular fashion to minimize the formation energy of the structures.

Cluster Expansion and DFT Analysis

Methodology

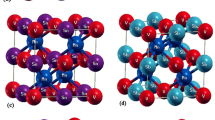
A Heusler material with formula $XY_{2}Z$ consists of four interpenetrating fcc sub-lattices, A, B, C,  and D (see Fig. 1). The sub-lattices include the points (0,0,0), (0.25, 0.25, 0.25), (0.5, 0.5, 0.5), and (0.75, 0.75, 0.75), which are occupied by $Y, X, Y'$ and Z atoms, respectively. In the XYZ HH, or so-called sub-Heuslers, only three of the four sub-lattices are occupied, A, B,  and D—see the cubic unit cell shown in Fig. 1—while the C sub-lattice is left empty. The HH structure has a $F{\bar{4}}3m$ symmetry. We model three HHs, namely VCoSb, NbCoSb, and TaCoSb, and study the introduction of vacancies (Vac) at the B sub-lattice occupied by atoms (M = V, Nb, Ta). The sub-lattice B is filled with a fraction 1–x of M atoms, and the other two sub-lattices, A and D, remain filled with atoms Co and Sb, respectively.

Fig. 1

(Color online) (a) $2\times 2\times 1$ HH cubic cell with formula MCoSb (M = V, Nb, Ta), M atoms are colored in cyen, Co and Sb atoms are in gray and brown, respectively. The black frame highlights one single cubic cell. The sub-lattices A, B and D, together with the empty C sub-lattice (not shown), define the primitive unit cell.

We use the CE technique in which the formation energies are calculated with density functional theory (DFT) for a set of $M_{1-{\mathrm{x}}}$Vac$_{{\mathrm{x}}}$CoSb structures with a different number of vacancies and atomic arrangements. Here we use the notation $M_{1-{\mathrm{x}}}{\mathrm{Vac}}_{\mathrm{x}}$CoSb to explicitly indicate that a vacancy of a M type atom is treated as a pseudo-atom. These formation energies of the structure are then approximated by a function that is expanded in small clusters within active sub-lattices. It means that besides the on-site energy of a single atom occupying a sub-lattice, the subsequent orders expanding the function include clusters of an increasing number of sub-lattice sites: tuples of two sites, sets of three sites, and so on. The largest distance between two sub-lattice points defines the size of the cluster. The treatment of vacancies as pseudo atoms allows us to compute effective interactions among atoms and vacancies. The active sites are the positions defined by the equivalent points of symmetry for the B-sub-lattice where M atoms or vacancies are hosted.³⁵ By calculating DFT energies for new configurations and adapting the CE, the process is iterated and the formula for the formation energy is improved.³⁶ The CE is considered satisfactory when the tested configurations provide a suitably low value for the so-called cross-validation (CV) score (Table I).

Table I Structural parameters, coordination number Co$M_{\mathrm{n}}$, and structural energies calculated by DFT

For the DFT calculations, we used the projector augmented wave method³⁷ as implemented in the Vienna ab initio simulations package.^38,39 The energy cut-off for the expansion of the electronic wave function in plane waves was set to 390 eV, while the type of exchange–correlation functional chosen was the Perdew–Burke–Ernzerhof generalized gradient approximation; an 8 × 8 × 8 Monkhorst pack k-mesh for the Brillouin integration was selected. Magnetic effects were considered throughout the spin-polarized electronic DOS within the local spin density approximation. Structural optimization was taken into account by allowing the relaxation of the unit cell, ion positions, and lattice parameters. Any force larger than 6 meV/Å was relaxed with a maximum of 12 ionic steps. Energies below 0.1 meV were used as a self-consistency criterion to stop the calculations. In this work, we obtained a score of CV = 0.061, 0.047, and 0.060, using 103, 216, and 164 structures for V-, Nb-, and Ta-based systems, respectively.

Results

Figure 2a–c shows the DFT energies calculated for the three HH systems, all of them presenting a minimum energy at 20% of vacancy concentration ($x=$ 0.2). The structure with the lowest energy corresponds to a unit-cell with 19 atoms (5 Co atoms, 5 Sb atoms, and 4 M atoms, see the Supplemental Material for a cif file). Henceforth, we use the notation $M_{0.86}$ and $M_{0.83}$, for systems with vacancy concentrations of 1/7 and 1/6, respectively. In all three MCoSb systems, the lowest energy atomic configuration also corresponds to the same unit cell; however, among them, the V$_{0.8}$CoSb has the highest energy of formation, − 0.48 eV, while Nb$_{0.8}$CoSb and Ta$_{0.8}$CoSb are − 0.73 eV and − 0.82 eV, respectively, indicating that the latter two are more stable. Notice that other unit cells with 20% of vacancies were also created during the CE procedure, but they have higher energies (see Discussion below).

Fig. 2

DFT energies calculated for the structures in the HH systems: (a) V$_{1-{\mathrm{x}}}$CoSb , (b) Nb$_{1-{\mathrm{x}}}$CoSb, and ©) Ta$_{1-{\mathrm{x}}}$CoSb.

From Fig. 2, we can also see that V$_{1-{\mathrm{x}}}$CoSb has a lower affinity to host vacancies, as is deduced from the slope, dE/dx, formed between the two points (E = 0, x = 0) and (E = 0.41 eV, x = 0.2). It has a less negative slope within the x range [0, 0.2] than the slopes formed for Nb$_{1-{\mathrm{x}}}$CoSb and Ta$_{1-{\mathrm{x}}}$CoSb. The lattice parameter for the most stable structures below $x \le$ 0.2 listed in Table II shows that vacancies reduce the volume of the unit cells monotonously. For a given x, V$_{1-{\mathrm{x}}}$CoSb HHs present smaller lattice parameters than Nb $_{1-{\mathrm{x}}}$CoSb and Ta$_{1-{\mathrm{x}}}$CoSb.

Table II Lattice parameters in $\text{\AA}$ for some selected stable structures for the three M$_{{\mathrm{x}}}$CoSb (M = V, Nb, Ta) HHs within the 0.0 $\le$ x $\le$ 0.2 range

We should point out that, at a very high concentration of vacancies, our model may not describe well the procedure of the synthetization of the materials, where, for instance, secondary structures like Nb$_3$Sb are observed. Notice that the complete removal of M atoms, $x=1$ point in Fig. 2, corresponds to the zinc blende structure for the CoSb binary system. Nevertheless, we expect that our model can describe concentrations below the 30% limit, where the HH phases strongly dominate the material.

The higher stability of the structures in M$_{1-{\mathrm{x}}}$CoSb, as more vacancies are introduced is reflected in the electronic DOS, especially in the gaps seen at negative energies for the parental structures, which are shifted towards energies closer to the Fermi level until they form a semiconducting gap at $x=0.2$. We follow this process in Fig. 3. Without vacancies, NbCoSb and TaCoSb behave like metals, while VCoSb is a semi-metal. At near 17% of vacancies, the three systems reduce their DOS to around the Fermi level. In this range of concentrations, the DOS structures are similar to those of n-doped semiconductors. Note that V$_{0.83}$CoSb is still semi-metallic; in addition, its Fermi level is positioned slightly deeper into the conduction band than the corresponding Fermi levels of Nb$_{0.83}$CoSb and Ta$_{0.83}$CoSb. Furthermore, the gap of V$_{0.83}$CoSb is smaller than those of Nb$_{0.83}$CoSb and Ta$_{0.83}$CoSb. A semi-conducting gap is fully formed at 20% of vacancies, with the Fermi level lying exactly at the edge of the valance band for the three systems. The gap widths are 0.72 eV, 1.0 eV, and 1.12 eV for V$_{0.8}$CoSb, Nb$_{0.8}$CoSb, and Ta$_{0.8}$CoSb, respectively. One can see that V$_{0.8}$CoSb has lost all traces of magnetism, as there is no dis-balance among the spin-up and spin-down electrons, nor in the conduction electrons, nor in the valance bands. The fact that, in the metallic states, electrons from the cations which are located in the conduction band participate in the bonding, but weakly,²⁰ via the overlapping with the Co atoms (see red and green lines in the DOS of Fig. 3) facilitates the formation of vacancies when the chemical bonds break.

Fig. 3

(Color online) Spin-resolved density of states, plotted in black, for V$_{1-{\mathrm{x}}}$CoSb (left panels), Nb$_{1-{\mathrm{x}}}$CoSb (center panels), and Ta$_{1-{\mathrm{x}}}$CoSb (right panels). The first, second, third and fourth rows correspond to x = 0, $x \approx$ 0.17, x = 0.20 and x = 0.25, respectively. The red lines are the contributions from the cation atoms, and the green lines from the Co atoms.

A further increase of the vacancies shifts the Fermi level into the valance bands for Ta$_{0.75}$CoSb, giving it a p-semiconducting character. Interestingly, for V$_{0.75}$CoSb and Nb$_{0.77}$CoSb (see Supplementary Material), we observe some electronic states forming in-gap states, separated by 0.12 eV and 0.23 eV, respectively, from the valence states. These in-gap states present different spin-polarizations: while the one in V$_{0.75}$CoSb is not polarized, the in-gap states in Nb$_{0.77}$CoSb are fully polarized. In the former case, the net magnetization is 0, while in the latter, it is 0.12 $\mu _{\mathrm{B}}$. Indeed, at 25% of vacancies, the three compounds present different DOS distributions around the Fermi level. At this vacancy concentration, the in-gap states are seen only in V$_{0.75}$CoSb. For Nb$_{0.75}$CoSb, the magnetization increases to 0.22 $\mu _{\mathrm{B}}$, but the full polarized in-gap of Nb$_{0.77}$CoSb has disappeared (see Figs. S2, S3 and Table S1 of the Supplemental Material); instead, spin-up states appear just below the Fermi energy and the spin-down states just above it. For Ta$_{0.75}$CoSb, the electronic states of both spin channels remain practically identical, with a small dis-balance between both types of spins at around 0.4 eV above the Fermi energy.

To understand the differences between the three $M_{0.75}$CoSb HH, it is crucial to first observe the peaks of DOS below the Fermi-energy (marked as P and $P'$ in Fig. 3) at the $M_{0.8}$CoSb compositions. Our interpretation is that the extra 5% of vacancies deplete the states previously lying in V$_{0.8}$CoSb below the Fermi level and close to the P peaks. The new position of the Fermi level for V$_{0.75}$CoSb falls below the peak P; importantly, the remaining amount of electron states allows the keeping of an equal population of up- and down-spins which lead to the unpolarized in-gap. In Nb$_{0.75}$CoSb, the depletion redistributes the DOS, creating the condition to meet the Stoner criteria at the level of the P energy. An exchange interaction splits the energy of states with different spins, with the states near the Fermi energy being spin-polarized, leading to the ferromagnetic state. In Ta$_{0.75}$CoSb, the DOS around the Fermi energy becomes very flat and, therefore, the Stoner criteria is not fulfilled. We think that the extension of the cation’s d-wave function is a decisive factor in producing such a diverse electronic character. The more localized 3d-wave function of V keeps the DOS narrow but at high enough energies with respect to the Fermi energy to avoid the Stoner condition. Conversely, the broader 5d-wave function of Ta induces a widespread DOS, which also prevents meeting the condition. It is only the right extension provided by the 4d-wave of Nb which allows the proper DOS distribution to meet the Stoner criteria.

In addition to the ground states we have discussed above, the CE created other structures with higher energies. These structures can provide information about the expected crystallographic and physical quality of materials obtained by a manufacturing process that does not match the required condition to grow a crystal with the symmetry of the lowest energy structures. Therefore, it is important to address how much the electronic properties of higher energy states can deviate from those seen in the lowest energy state. As an example, we take a look at Ta$_{0.8}$CoSb. We plot in Fig. 4 the total DOS of three structures, which are 0.045 eV, 0.263 eV, and 0.483 eV higher in energy (energy per $M_{0.8}$CoSb formula) than the ground states. We label these three states S1, S2, and S3, respectively. The two states closer in energy to the ground states still present a semiconducting gap, but with reduced width; thus, for S1 the width is 0.89 eV, and for S2 is 0.37 eV. In contrast, for S3, the semiconducting gap has closed. Therefore, there is a fair possibility to observe semiconducting gaps smaller than 1.1 eV in Ta$_{0.8}$CoSb grown under techniques that do not allow the highest control to obtain materials with the ground state symmetries. Similarly, for V$_{0.8}$CoSb and Nb$_{0.8}$CoSb, a gap remains for structures with energies close to the ground states.

Fig. 4

(Color online) Total DOS for four structures with the same Ta$_{0.8}$CoSb composition but different vacancy distributions. The DOS for the ground state is labeled G, the three other structures with higher energy are labeled S1, S2, and S3. The structures have the following order of formation energy: $E_{{\mathrm{GS}}}$ < $E_{{\mathrm{S1}}}$ < $E_{{\mathrm{S2}}}$ < $E_{{\mathrm{S3}}}$.

The coordination number formed by the Co and M (M = V, Nb) in the compound can help to explain the differences between the highest and lowest energy structures at a given $M_{0.8}$CoSb composition. In principle, the coordination number can take values from zero to four. Henceforth, we denote the number of M atoms bounded to a centered Co as CoM$_{\mathrm{n}}$ (n = 1, 2, 3, 4), where, for instance, CoM$_3$ means the coordination is reduced to three, due to the absence of one M atom. We will use Co$M_{\mathrm{n}}$ as indicators to compare structural stability. First of all, we notice that the DFT calculations for the same compositions predict higher energies of formation for cells with larger volumes than for cells with smaller volumes (see Table I). Moreover, the high energy cells present a clear tendency to have more Co$M_2$ and Co$M_4$ amounts than the low energy cells. We use these observations to prove that vacancy clustering is energetically not helpful for the stability of cation-deficient HHs. To illustrate our argument, we focus on the lowest and the highest energies of Ta$_{0.8}$CoSb cells discussed in Fig. 4. Thus, for S4-Ta$_{0.8}$CoSb (energy formation − 0.65 eV), Co$M_2$ = 1 and Co$M_3$ = 2, $M_4$ = 2, while for S2-Ta$_{0.8}$CoSb (energy formation − 0.73 eV), Co$M_2$ = 1, Co$M_3$ = 3 and Co$M_4$ = 1. In the lowest energy structure, G-Ta$_{0.8}$CoSb (energy formation − 0.88 eV), Co$M_2$ = 0, Co$M_3$ = 4 and Co$M_4$ = 1 (the S2-Ta$_{0.8}$CoSb and G-Ta$_{0.8}$CoSb unit cells and the different Co$M_{\mathrm{n}}$ coordinations are shown in Fig. S1 of the Supplementary Material). One infers from this that the simultaneous appearance of two and four coordinations in the higher energy structures is because there are regions that contain close voids formed by the vacancies, while, in the lowest energy cells, the absence of two coordinations but the increased presence of three coordinations is due to the more homogeneous distributions of the void spaces. Hence, this indicates that the proximity of the vacancies forms large volumes, which in turn creates larger instability. Similar tendencies are seen for structures with the V$_{0.8}$CoSb and Nb$_{0.8}$CoSb compositions.

In some high-energy cells, the vacancies arrangements form such disconnected regions that they look structurally very unlikely to occur in practice. That is, for instance, the case of the only high-energy point at the V$_{0.8}$CoSb composition seen in Fig. 2a, and denoted as S1-Ta$_{0.8}$CoSb in Table I. The vacancies have created single Co-V pairs (Co$M_1$ = 1) and a higher amount of Co-V coordinations (Co$M_4$ = 3), and these result in the disconnected slaps seen in the extended S1-Ta$_{0.8}$CoSb presented in Fig. S1d of the Supplementary Material. In contrast, the most stable $M_{0.8}$CoSb structures look denser, as observed in the extended versions of the G-Ta$_{0.8}$CoSb cell presented in Fig. S1c of the Supplementary Material.

The vacancy arrangement is analyzed in Table III by investigating the superstructures created by the vacancies. At the same time, the data provide information about the self-organization of the vacancies as their concentration increases. We use the I-shell concept of vacancies separated by an fcc lattice vector, $\mathbf {R}_{\mathrm{i}}$, to count the site occupation, defined as $n_{\mathrm{i}}$ (In Table III, the first three columns give pertinent information for the first nine shells). Due to the fewer number of vacancies, it seems that it is energetically possible at x = 1/7 to accommodate six vacancies in the third shell (two less than for x = 1/6 and 1/5 concentrations), while keeping without vacancies the nearest neighbors (NN), next nearest neighbors (NNN), and the fourth shell. For x = 1/6 and x = 1/5, both concentrations can avoid the high-energy cost of having NN vacancies. At x = 1/5, we see the first composition, $M_{0.8}$CoSb, presenting NNN vacancies as a result of the large number of vacancies introduced. In the next section, we will define an order parameter that characterizes these superstructures. Moreover, we will test the stability of the ground states against thermal fluctuations and follow their order–disorder transition. In Fig. 5, we provide an auxiliary cell to enumerate the atoms which are located in the I-shell.

Fig. 5

(Color online) Auxiliary structure displaying only the fcc sub-lattice B of a $2\times 2\times 3$ HH cell. The enumerated sites are located in the I-shell around the B-sub-lattice, which is labeled 0.

Table III Occupation of the I-shell at 200 K for the M$_{0.86}$CoSb, M$_{0.83}$CoSb and M$_{0.80}$CoSb ground states; denoted, respectively, as $n_{\mathrm{i}}(1/7)$, $n_{\mathrm{i}}(1/6)$ and $n_{\mathrm{i}}(1/7)$

Monte Carlo (MC) Simulations

Methodology

MC simulations using the interaction coefficients (ICs) of the CE can access the configurational energy of larger atomic configurations, which in turn allows us to analyze collective behaviors as well as to study temperature effects. This is achieved by utilizing the Metropolis algorithm,⁴¹ which exchanges the positions of atoms and vacancies at a given temperature. To this end, we perform MC simulations in the canonical ensemble to study order–disorder transitions at finite temperatures. At each temperature, we let the code run for a certain MC time and a certain number of MC steps until the energy has achieved a precision of 0.001 eV. We use systems which include active lattice sites, ${N}_{\mathrm{act}}$, originated from the B sub-lattice. Simulations with a fraction x of vacancies are performed with a fixed number $N_{{\mathrm{Vac}}}\simeq xN_{\mathrm{act}}$ of vacancies and number $N_{{\mathrm{M}}}=N_{\mathrm{act}}-N_{{\mathrm{Vac}}}$ of M atoms. In the simulations, one MC cycle consists of $N_{\mathrm{act}}$ single steps, in which one active site for an M atom and one for a vacancy are randomly chosen. The old configuration is changed into a trial configuration by swapping the atom and vacancy of the two sites. Following the Metropolis algorithm,⁴¹ the trial configuration is accepted or rejected. The number of active lattice sites used for the simulations was between 171,500 and 274,625.

We should confirm that, in our canonical procedure, once the numbers of Nb atoms and vacancies are fixed, their energy contribution is simply subtracted. With the semi-grand canonical ensemble, which is can be employed in the ATAT software package, it would be possible to find the ratio of equilibrium between Nb atoms and their vacancies at a given temperature. This is because, during the implementation of CE, the chemical potentials are also calculated.

To quantify the degree of ordering at a given vacancy concentration and temperature (T), we define an order parameter (OP)^42,43,44 for two vacancies separated by an fcc lattice vector $\mathbf {R}_{\mathrm{i}}$ as:

$$\begin{aligned} O(R_{\mathrm{i}}, x;T)=\frac{P(i, x; T)-x}{1-x}, \end{aligned}$$

(1)

where I is the coordinate shell of the lattice vector centered around a vacancy. P(I, x, T) is the probability at temperature T of such a shell to be occupied by vacancies, and we calculate it by means of

$$\begin{aligned} P(R_{\mathrm{i}}, x; T) =\frac{C_{\mathrm{i}}/Z_{\mathrm{i}}}{xN_{\mathrm{act}} }. \end{aligned}$$

(2)

Here $C_{\mathrm{i}}$ is the number of vacancies counted in the I-shell during an MC step, and $Z_{\mathrm{i}}$ is the coordination number of that shell. The form of Eq. 1 measures the deviation of vacancy occupation with respect to a statistical average distribution: if the OP matches this average, it is zero for an average occupation. If $O(R_{\mathrm{i}}, x;T)$ takes negative values, this indicates that vacancies avoid being placed in the I-shell relative to a centered vacancy, while if they are positive, there is a tendency for that shell to be filled by vacancies. If $O(R_{\mathrm{i}}, x;T)$ is positive, the vacancy concentration in the I-shell is larger than average. We can consider the combination of values taken by the I-th order parameter of a composition, $O(R_{\mathrm{i}}, x;T)$, with $I=1, 2, \ldots 9$, as real space fingerprints of the structures we will discuss.

We highlight some relevant features of atomic-vacancy arrangements extracted from the first OPs of the ground states without the effects of the temperature in Table III. For instance, with 17% of vacancies, one has $O(R_{\mathrm{i}}, x;T)$ = − 0.2, indicating a scarcity of vacancies in the NN and NNN shells, while, for I = 4, 5, values close to 0 indicate average vacancy concentration. Here, it is worth mentioning that these two last vacancy occupations coincide with a random homogenous distribution, although they are intrinsically ordered. Increasing the amount of vacancies to 20% leads to an OP for NN without vacancies to a value of − 0.25.

Results

We performed MC simulations using the ICs obtained by the fitting of CE to the number of structures created in the “Cluster Expansion and DFT Analysis” section. For the MC simulations, we restricted ourselves to Nb$_{\mathrm{x}}$CoSb. The other two materials behave very similarly. We followed the change in energy as we decreased the temperature in an initial structure formed by the random distribution of vacancies. The initial structure was created by applying the MC simulations at 4000 K, an artificial state, just chosen for numerical reasons in order to achieve a completely disordered initial state. We investigated systems for $x=0.8$ and close by concentrations. It turned out that, while the CE obtained from the standard ATAT process is well suited to study ground states, it does not perform well at higher temperatures. In fact, the internal energy increased at a distinctly too high energy, indicating that higher energy states are not satisfactorily represented. The reason is that the ATAT procedure had found only a very few higher energy states for $x=0.8$. Therefore, we refined the description of the Nb$_{0.8}$CoSb composition by instructing the CE to consider high-energy disorder structures throughout the inclusion of special quasi-random structures (SQS). We create 14 supercells with the help of the SQS algorithm (see Zunger et al. in⁴⁵), and subsequently, we applied the CE to the 230 extended sets of Nb$_{{\mathrm{x}}}$CoSb structures, which gave CV = 0.043 during the fitting procedure.

Once we have obtained the ICs for each set, we can analyze the energy dependence with the temperature (the results are displayed in Fig. 6a). We notice an important modification to the curve without SQS structures (labeled as No-SQS in Fig. 6a): The new curves present lower phase transition temperatures than the corresponding energy curves for MC with no SQS supercells. We should mention that, in previous CE²⁶ trying to describe the same system, − 0.605 eV of energy was reported in the low-temperature regime, which is higher than the energy we found, indicating that our MC simulation has been able to find a lower energy arrangement of vacancies than the states in Ref. 26.

Fig. 6

(Color online) (a) Temperature energy dependence in Nb$_{0.8}$CoSb when no SQS supercells are included in CE (orange curve, right axis) and when the SQS supercells are taken into account (green curve, left axis), (b) order parameters in Nb$_{0.8}$CoSb when configurational entropy is considered. Numbers label the corresponding atomic shells.

We looked into the order parameters and MC snapshots to collect information about the different effects of temperature on the atomic ordering. The temperature changes of OPs for the MC simulation (Fig. 6b) follow a similar trend, as its corresponding energy curve shows in Fig. 6a; importantly, the regions where they change their slope are within the range where the energies show the transition temperatures. The OPs bring help to reveal information about the preferred arrangement of the vacancies. The − 0.2 value for NN vacancies at low temperature indicates a strong reduction in the likelihood of finding vacancies at these lattice positions. The two next reduced likelihoods correspond to the fourth and sixth shells. On the other hand, the OP shows that vacancies tend to be located at the third shell, while some traces of medium-ranged order are developed in the eighth shell.

The snapshots complement the information reported by the OPs. The ordering created in Nb$_{0.8}$CoSb is shown in the snapshot of Fig. 7. A close look at it reveals three main characteristics: (1) the system is not homogeneous, rather it presents domains with well-defined patterns; some domains being separated by defective or weakly ordered states; (2) the structures differ from those of the ground state; and (3) the vacancies form distinct patterns along the {110} direction, or equivalent orientations. The patterns change from line to line in a non-obvious way. In general, one finds either one single vacancy or a pair of NN vacancies every second or third Nb atom. The black contour depicts a set of such arrangements in Fig. 7. Note also the lines formed by Nb atoms which run parallel to the lines of the vacancy patterns (see, for instance, the region marked in blue in Fig. 7). Previous studies applying the CE expansion have also shown that two vacancies prefer to be located in the third shell.³¹ However, based on the reported snapshots and analysis of the real-space distribution of vacancies, our MC simulations seem to develop higher medium-range ordering. Similarly, with the MC snapshots plotted in Ref. 26, it is difficult to conclude whether or not any type of short- to medium-range ordering is present. Perhaps these observations can be explained because, in our MC simulations, we used much larger systems. And, instead of truncating or selectively removing terms of the CE, we used the full CE, which may lead to lower energy states corresponding to higher ordering, as we commented at the end of the second paragraph of this section for Fig. 6a.

Fig. 7

(Color online) Snapshot showing at 300 K the atom–vacancy arrangements in Nb$_{0.8}$CoSb obtained by MC simulations.

Conclusions

With the help of a cluster expansion method, we studied the structural formation in VCoSb, NbCoSb, and TaCoSb when the concentration of vacancies at the cationic site is increased. The method proved unambiguously that the systems are more stable at 20% of concentration and, according to the DFT calculations in the range 0–20%, there is a metal–semiconductor transition. The transition in VCoSb includes a magnetic–nonmagnetic transition, while the other two systems remain non-magnetic. Further increase of the vacancies may lead to an n-doped semiconductor or to in-gap states. The energy of formation and width of the gaps calculated in the three HH make us conclude that, at 20% of vacancy concentration, Ta$_{0.8}$CoSb is the most stable, closely followed by Nb$_{0.8}$CoSb, while V$_{0.8}$CoSb is the least stable of the three HHs.

This theoretical result predicts a slightly higher vacancy concentration than the experiments, where the stable stoichiometry of one of the compounds is found at 1/6 vacancies.³² We should point out that the CE method deals simultaneously with the depletion of electrons and the distribution of them across the material as the amount of vacancies increases (see the Discussion for how the coordination number affects the chemical bonding of the system in Table I, and also the case of (V, Nb)TaCoSb⁴⁶). It is worth noting that one expects a larger lattice distortion as the amount of vacancies increases. In this regard, although we included atomic relaxation for all the structures displayed in Fig. 2 in our DFT calculation, cooperative lattice distortions in extended systems may favor lower energies for 1/6 than for 1/5 of vacancies.

According to the combined information of our DFT and MC results, the choice of synthetization is crucial to obtain the maximum semi-conducting gap: only under very controlled methods can the most stable structures and corresponding gaps be delivered. However, other metastable structures with less refined synthetization methods should be fairly accessible, albeit with a reduced gap. The lower lattice thermal conductivity of defective HHs, and the close relationship between vacancy concentration and short-range order,^47,48 strongly suggest the continuation of studies to establish optimal atomic arrangements⁴⁹ which can lower the lattice thermal conductivity without compromising too much the electronic transport properties. In this sense, our results also show that heat treatment can be used to manipulate the amount of vacancy-ordered structures.