Introduction

Spectroscopy is utilized in various research fields such as physics, chemistry, agriculture and medical science, and delivers valuable insights and knowledge. Spectroscopic data based on light, x-rays and electrons is often obtained using charge-coupled device (CCD) detectors,1,2,3,4 and the number of pixels in the arrays is sometimes insufficient. In Raman spectroscopy, for example, peak positions are slightly shifted depending on the temperature, carrier concentration and strain in semiconductors and low-dimensional materials.5,6,7,8,9,10,11,12,13,14,15 However, due to the limitations imposed by the number of CCD elements in the array in a Raman apparatus, a narrowed data interval is achieved at the expense of narrowing the range of wavelengths measured. Therefore, it is almost impossible to acquire Raman spectra with a narrow data interval over a wide range. Curve-fitting with a model function such as Lorentzian, Gaussian or Voigt functions is used to interpolate the values between data points and analyse slight shifts in the Raman peak positions. Although the curve-fitting provides the most plausible solution within the constraints of the fitting model and one can obtain valuable information about the peak position with much better precision than the data interval in most cases, actual experimental spectra always more or less deviate from the ideal spectra expressed by the fitting model function. The slight deviation from the fitting model function evokes systematic errors in the estimation of peak positions.6,16,17 Although it is possible to narrow the data interval through the acquisition of spectroscopic data with sub-pixel displacements, the precision of the displacements limits the data interval that can be achieved.18 This is true not only for Raman spectroscopy but also for other spectroscopic methods.19,20

Bayesian image super-resolution is a method to combine a set of low-resolution images of the same view with sub-pixel displacements relative to each other using Bayes’ rule in order to obtain a single image of higher resolution. In this method, the sub-pixel displacements and high-resolution image are deduced from a set of low-resolution images assuming a prior distribution.21,22,23 In the present study, we applied the concept of Bayesian super-resolution to spectroscopic data to increase the number of data points and precisely characterize the spectral shape of Raman scattering peaks. Note that the word “resolution” has different meanings within different fields. In the field of digital image processing, “resolution” means the pixel interval length, which is simply calculated by dividing the width of the image into the number of pixels. This is totally different from the meaning of spectral resolution, which is defined as the minimum wavenumber, wavelength, or frequency difference between two lines in a spectrum that can be distinguished. In this manuscript, the word “super-resolution” is used to mean not that the spectral resolution is increased, but that the data interval is narrowed.

Bayesian Super-Resolution

In this section, the procedure of Bayesian super-resolution of spectroscopic data is described followed by a demonstration of Bayesian image super-resolution.22,23,24 One of the most important differences between images and spectroscopic data is the dimension of the data. While image data is two-dimensional, spectroscopic data is one-dimensional, with one variable corresponding to the horizontal axis (e.g. wavenumber in the case of Raman spectra). Reconstruction-type super-resolution aims to generate a spectrum with a narrow data interval x from a given set of observed spectra with a wide data interval D = {yt | t = 1, 2, . . . , T} with transformation expressed by registration parameters θ. Here, we denote all observed spectra and registration parameters collectively by y = [y1, . . . , yT] and θ = [θ1, . . . , θT]. Bayesian super-resolution starts by defining two fundamental probability distributions: the prior distribution on a spectrum with narrow data interval p(x) and the conditional probability, or likelihood, p(yt | x, θt) of an observation yt given x and the registration parameters θt. From these two distributions, the spectrum with a narrow interval can be deduced based on the posterior distribution p(x | D, θt), which is given by the prior estimate and the likelihood according to Bayes’ rule:

$$ p\left( {{\varvec{x}}{|} D, {\varvec{\theta}}} \right) = \frac{{p\left( {\varvec{x}} \right)p\left( {D{|}{\varvec{x}}, {\varvec{\theta}}} \right)}}{{p\left( {D{|}{\varvec{\theta}}} \right)}} = \frac{{p\left( {\varvec{x}} \right)\mathop \prod \nolimits_{t = 1}^{T} p\left( {{\varvec{y}}_{{\varvec{t}}} {|}{\varvec{x}}, {\varvec{\theta}}_{{\varvec{t}}} } \right)}}{{p\left( {D{|}{\varvec{\theta}}} \right)}}. $$
(1)

Bayesian super-resolution estimates the parameters using the maximum-marginalized-likelihood (MML) rule:

$$ \widehat{\theta } = \arg \mathop {\max }\limits_{\theta } L\left( \theta \right), $$
(2)

where L(θ) is the log marginal likelihood as follows:

$$ L\left( {\varvec{\theta}} \right) = \ln \smallint d\user2{x }p\left( {\varvec{x}} \right)p\left( {D{|}{\varvec{x}}, {\varvec{\theta}}} \right). $$
(3)

After obtaining the estimated registration parameters (\(\hat{\theta }\)), the spectrum with a narrow interval (\(\hat{x}\)) is deduced as the expected value of the posterior distribution:

$$ \widehat{x} = E\left( x \right) = \int dx~xp\left( {x|D,\widehat{\theta }} \right). $$
(4)

Here, we use a prior estimate which represents the smoothness constraints given by the following formula as given in Kanemura et al.23:

$$ p\left( {\varvec{x}} \right) = \frac{1}{Z}exp\left\{ { - \frac{\rho }{2}\mathop \sum \limits_{i\sim j} \left( {x_{i} - x_{j} } \right)^{2} } \right\} = Gauss\left( {{\varvec{x}}{|}0, \rho^{ - 1} A^{ - 1} } \right) $$
(5)

where ρ is a precision parameter that determines the strength of the prior belief and i ~ j represents the adjacent values i and j, and the summation is taken over all pairs of neighbouring values. Here, we express the pair of neighbours of the value i on the spectrum with a narrow interval as N(i). In this case, p(x) becomes a Gaussian distribution because the exponent of Eq. 5 is always negative and is a quadratic function of x. A is a symmetric matrix that is derived as follows:

$$ A_{ij} = \left\{ {\begin{array}{*{20}l} {\left| {N\left( i \right)} \right| \quad\left( {i = j} \right)} \\ { - 1 \quad\left( {i \sim j} \right)} \\ {0\quad \left( {otherwise} \right)} \\ \end{array} } \right.. $$
(6)

The likelihood is defined according to the assumption that the observed spectrum yt is obtained by an operation in which the spectrum with narrow interval x is geometrically transformed and corrupted by Gaussian noise. In the present study, only horizontal translation of spectral data is considered. This operation can be represented by the following equation using registration parameters θt:

$$ {\varvec{y}}_{{\varvec{t}}} { } = { }W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right)x{ } + { }\varepsilon_{t} ,{ }\varepsilon_{t} { }\sim { }Gauss\left( {0,\beta^{ - 1} { }I} \right), $$
(7)

where W(θt) is a non-square matrix representing the geometrical transformation and εt is Gaussian noise with uniform precision (inverse variance) β. We sometimes write Wt = W(θt) for the sake of simplicity. The likelihood is given by

$$ p\left( {{\varvec{y}}_{{\varvec{t}}} {|}{\varvec{x}}, {\varvec{\theta}}_{{\varvec{t}}} } \right) = Gauss\left( {{\varvec{y}}_{{\varvec{t}}} {|}W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right){\varvec{x}},\beta^{ - 1} I} \right). $$
(8)

The expectation–maximization (EM) algorithm is used to search the registration parameters.25 In the E step, the posterior distribution of a spectrum with narrow interval x is calculated:

$$ p\left( {{\varvec{x}}{|}D, {\varvec{\theta}}} \right) = Gauss\left( {{\varvec{x}}{|}{\varvec{\mu}}, {\Sigma }} \right), $$
(9)

where

$$ {{\varvec{\Sigma}}} = \left( {\rho A + \beta \mathop \sum \limits_{t = 1}^{T} W_{t}^{T} W_{t} } \right)^{ - 1} $$
(10)
$$ {\varvec{\mu}} = \beta {\Sigma }\left( {\mathop \sum \limits_{t = 1}^{T} W_{t}^{T} {\varvec{y}}_{{\varvec{t}}} } \right). $$
(11)

In the M step, the following expected squared error derived from the expected likelihood is optimized with respect to θt:

$$ \mathop \sum \limits_{t = 1}^{T} E\left( \Vert{{\varvec{y}}_{{\varvec{t}}} - W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right){\varvec{x}}\Vert^{2} } \right) = \mathop \sum \limits_{t = 1}^{T} E\left\{ \Vert{{\varvec{y}}_{{\varvec{t}}} - W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right){\varvec{\mu}}\Vert^{2} + tr\left( {{\Sigma }W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right)^{T} W\left( {{\varvec{\theta}}_{{\varvec{t}}} } \right)} \right)} \right\} $$
(12)

The procedure of super-resolution for spectroscopic data is summarized in Algorithm 1.

figure a

Spectroscopic data D is composed of observed values of yt (corresponding to the values of “intensity” in Raman spectra for example) at each horizontal position θtp (with values of “wavenumber”), which was determined by the measurement apparatus (for example, the interval of the data points is not constant in CCD Raman data). In addition, the deviation of the horizontal position from the ideal position θtc exists as a hidden parameter. Thus, in the present case, θt is composed of θtp and θtc. In the present study, the expected squared error shown in Eq. 12 was optimized in the parameter of θtc by brute-force search because of its multimodality.

Determination of Hyperparameters

In the algorithm for our Bayesian super-resolution of spectroscopic data, there are two hyperparameters ρ and β. In this section, the determination procedure for these hyperparameters is shown. We set the value of 1/β as the value of the variance for the background noise of the observed spectroscopic data. The value of ρ was determined from the virtual spectroscopic data generated by the following procedure. Firstly, the experimental data was fitted to the Lorentzian and the values of peak height (I0), peak position (x0), vertical offset (F0) and full width at half maximum (FWHM) (w) were estimated. The Lorentz function [(F(x)] is defined as follows:

$$ F\left( x \right) = F_{0} + I_{0} \frac{{w^{2} }}{{4\left( {x - x_{0} } \right)^{2} + w^{2} }}. $$
(13)

Then, the virtual spectroscopic data was generated from the Lorentz function using the estimated values with the noise and geometrical transformation represented by the registration parameters θt. Using the virtual data, the value of ρ was determined so as to minimize the error from the Lorentz function. Using these hyperparameters, the spectrum with a narrow data interval was deduced from the actual data with the promised precision.

Experimental Procedure

The Si substrate for positron defect measurements (NMIJ CRM 5606-a) was obtained from the National Metrology Institute of Japan. Itoh and Shirono reported that the Raman shift of NMIJ CRM 5606-a is 520.45 ± 0.28 cm−1 with reliable estimation from their intensive research.26 Raman spectroscopy measurements were performed at room temperature using a Renishaw In-Via Raman microscope. The wavelength of the incident laser was 532 nm and the width of the grating was 3000 gr/mm. The data interval of the observed spectrum was about 0.8 cm−1 at around 520 cm−1. An objective lens with a magnification of five times was used, and the acquisition time was 1 s. A total of 200 Raman spectra were obtained by changing the horizontal offset values by 0.01 cm−1. Note that the precision of horizontal offset is not important because the offset values were deduced from the algorithm as the registration parameters θt.

Results and Discussion

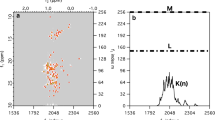
Figure 1a shows one of the Raman spectra taken from the Si substrate. Owing to the edge filter, the background levels showed a steep change at around 100 cm−1. In addition to the Raman shift of Si at around 520 cm−1, leakage of Rayleigh scattering at around 0 cm−1 was observed. All Raman shifts were evaluated by fitting to the Lorentzian functions (Fig. 1b), and the peak intensities and peak positions were confirmed to be randomly distributed as shown in Fig. 1c. The evaluated parameters obtained by fitting and the evaluated value of the standard deviation for background noise are summarized in Table I.

Fig. 1
figure 1

One of the Raman spectra taken from the Si substrate (a) and the result of Lorentzian curve-fitting (b). The values of the peak intensity and wavenumber for all measured Raman shifts evaluated by curve-fitting (c).

Full size image
Table I Evaluated values of the Raman spectra obtained by Lorentzian fitting
Full size table

Two hundred sets of virtual spectroscopic data were generated, and the error of the super-resolution spectra from the true values calculated from the Lorentz function was evaluated for different values of ρ. In the present case, the data interval was set to 0.01 cm−1, which was about 1/80 of that for the observed spectra. From the result shown in Fig. 2, we set the value of ρ as 2.6 × 10−1. The average error of the reconstructed spectrum with a narrow data interval from the Lorentz function was as low as 3.31, which is almost the same as the estimated standard deviation obtained with 200 measurements (σ200 = 3.01), which indicates that the Bayesian super-resolution succeeded in achieving both high resolution by Bayesian super-resolution and the reduction of noise by data accumulation.

Fig. 2
figure 2

Average error of the reconstructed spectra from the true values calculated from the Lorentzian function for different values of ρ.

Full size image

The Raman spectrum with a narrow data interval was reconstructed by the Bayesian super-resolution procedure using the hyperparameters determined by the virtual experiment. Figure 3 shows the reconstruction result of the super-resolution Raman spectrum from the 200 experimental data sets as an average value corresponding to Eq. 11. Although the spectrum shown over the wide range (Fig. 3a) seems almost the same as the experimental spectrum shown in Fig. 1a, the magnified spectra clearly show the results of the super-resolution reconstruction. In the magnified spectra shown in Fig. 3b, c and d, the reconstructed spectrum seems to be a continuous line because the data interval was sufficiently narrow. Owing to the narrow data interval, the characteristic shapes of peaks, which were not noticed in the experimental spectra with a wide data interval, become apparent. The shape of the Rayleigh scattering peak at around 0 cm−1 shown in Fig. 3b was not ideal Gaussian but asymmetric. This would be due to the actual condition of the edge filters. At around 300 cm−1, very weak peaks originating from two-phonon Raman scattering,27,28 which was reported to appear at 302 cm−1, were observed as shown in Fig. 3c. Lorentzian curve-fitting of two-phonon Raman scattering with the measured data (green line in Fig. 3c) does not appear to precisely reconstruct the peak position and shape compared to the result of super-resolution. It may seem that this is hardly surprising considering that the reconstructed spectrum was generated from 200 spectra. However, this is not a matter of course, since 200 spectra were acquired with different offset values as shown in Fig. 1c and cannot simply be accumulated. The improvement of signal to noise ratio with narrowing of the data interval is a benefit of Bayesian super-resolution. At around 520 cm−1, the single-phonon Raman scattering of silicon was observed, which did not have the ideal Lorentz function shape (Fig. 3d). Further magnification of the spectrum shows the asymmetrical shape of the peak top, which may be caused by the deviation of the optical alignment from ideal.

Fig. 3
figure 3

(a) Result of super-resolution reconstruction of the Raman spectrum from 200 measured Raman spectra. (b)–(e) Magnified spectra, and one of the measured spectra is also shown for comparison.

Full size image

The deviation from the ideal Lorentz function for the Raman scattering as well as that from the ideal Gaussian function for the leakage of Rayleigh scattering led to the occurrence of systematic errors in the peak positions derived from fitting. On the other hand, we can determine the peak positions as the local maxima with a wavelength resolution of 0.01 cm−1 and the promised precision, estimated from the variance calculated by Eq. 10. Table II summarizes the peak positions and Raman shift for the Si substrate estimated from the results of the super-resolution spectra. The estimated Raman shift agreed with the reported values for NMIJ CRM 5606-a with good reliability.26

Table II Estimated values of peak positions and Raman shift from the results of super-resolution reconstruction as well as the value reported by Itoh and Shirono26
Full size table

The current results indicate that by applying Bayesian super-resolution to data from multiple measurements of Raman spectra obtained by a commercial CCD Raman apparatus, one can estimate the Raman shift with similar precision to that obtained by high-reliability methods. Furthermore, by the current procedure, in which the hyperparameters are determined by a virtual experiment, we can reconstruct the spectra with a narrow data interval and decreased noise by Bayesian super-resolution with excellent precision. The present methodology can be applied not only to Raman spectroscopy but to all kinds of spectroscopic methods utilizing multichannel detectors, such as electron energy loss spectroscopy (EELS), energy-dispersive x-ray spectroscopy (EDX), Auger electron spectroscopy (AES), x-ray photoelectron spectroscopy (XPS), x-ray fluorescence spectroscopy (XRF), x-ray diffraction (XRD), optical emission and absorption spectroscopy, photoluminescence spectroscopy (PL) and cathodoluminescence spectroscopy (CL).

Although the current methodology cannot improve the spectral resolution, which is mainly limited by the properties of the grating, prism of holographic elements, slit width, aberrations, spectrometer design and spectrometer focal length, precise estimation of features such as spectral peak positions and shapes is possible without changing the high-resolution setup of the spectroscopy apparatus. Especially in the application to Raman spectroscopy analysis, the present method will contribute to increasing the precision of the characterization of residual stress and impurity concentrations in electrical materials.

Conclusion

We established a methodology to narrow the interval of spectroscopic data by applying Bayesian super-resolution. In our present method, hyperparameters are determined by a virtual experiment imitating the experimental data, and the precision of the super-resolution reconstruction is confirmed by the calculation of errors from the ideal values. In order to validate the performance of the super-resolution reconstruction of spectroscopic data, we acquired 200 Raman spectra with a data interval of about 0.8 cm−1 from a reference Si substrate (NMIJ CRM 5606-a). Using the determined hyperparameters, super-resolution reconstruction with a data interval of 0.01 cm−1 was successfully achieved with the promised precision. From the result of the super-resolution reconstruction, the Raman scattering peak of the reference Si substrate was estimated as 520.55 (+0.12, −0.09) cm−1 which is comparable to the precisely determined value. The present methodology can be applied to various kinds of spectroscopic analysis, leading to increased precision in the analysis of spectroscopic data and the ability to detect slight differences in spectral peak positions and shapes. Especially when applied to Raman spectroscopy analysis, the present method will contribute to increasing the precision of the characterization of residual stress and impurity concentrations in electrical materials.