Introduction

GaN high-electron-mobility transistors (HEMTs) have shown great potential for use in high-power and high-frequency applications due to their wide bandgap and high electron mobility.1,2 The defining feature of this device technology is the presence of a high-density two-dimensional electron gas (2DEG) at the AlGaN–GaN interface due to the strong spontaneous and piezoelectric polarization. However, this high 2DEG density leads to GaN HEMTs that are normally-ON (depletion-mode) switches, which is not suitable for power electronic applications because of safety and system cost concerns. Therefore, the carriers in the 2DEG beneath the gate should be depleted to achieve normally-OFF (enhancement (E)-mode) transistors. Moreover, E-mode GaN HEMTs have attracted much attention for use in power switching applications, owing to their high breakdown voltage and low on-resistance.3,4,5,6,7,8,9

Several techniques have been used to design E-mode GaN devices, all of which incorporate technologies that empty the 2DEG channel underneath the gate at zero gate bias. The recessed-gate structure is one of the approaches for designing E-mode GaN HEMTs for use in power electronic applications.10

Understanding the physical mechanisms behind the formation of the 2DEG is crucial to model the 2DEG charge density under the gate and to device design.11 Experimental research has shown that the presence of donor states at the AlGaN surface is the main source of the electrons in the 2DEG.12,13 For non-recessed-gate GaN HEMT structures, Gordon et al.14 showed that the 2DEG density varies with the barrier layer thickness. It was subsequently shown experimentally as well as by numerical simulations that the Al mole fraction in the AlGaN has a significant impact on the 2DEG density due to its effect on the piezoelectric and spontaneous polarization.

In this paper, an analytical model for the 2DEG charge density of GaN HEMTs is presented and verified by a complete match with experimental data. Moreover, an analytical model for the recessed-gate GaN HEMT structure is also provided. In addition to the AlGaN barrier layer thickness (d) and the Al mole fraction (x) affecting the density of the 2DEG, the recess height (h) also influences the density of the 2DEG for recessed-gate GaN HEMTs. To design highly efficient and reliable E-mode HEMT structures, it is essential to understand the dependence of the 2DEG density on these physical characteristics.

Simulation of Non-recessed and Recessed-Gate GaN HEMTs and Comparison with Experimental Data

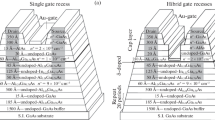
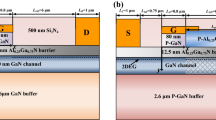
Figure 1 shows a schematic of an experimental GaN HEMT with the recessed-gate structure.10 The epitaxial structure consists of a 15.6-nm-thick AlGaN barrier layer with Al mole fraction x = 0.27 on a 2-μm-thick GaN buffer layer grown on a sapphire substrate. The devices are fabricated with Ti/Al/Ni/Au (20/120/20/70 nm) ohmic metallization at the source and drain. According to the gate, a 3-nm barrier is etched down by neutral-beam technology to recess the gate. After that, Ni/Au is deposited to form the gate electrode. The detailed fabrication process is explained in Ref. 15.

Fig. 1
figure 1

Schematic of a recessed-gate GaN HEMT structure.

Full size image

To achieve precise control over the recess etch rate, neutral-beam etching (NBE) is carried out, and the reduced AlGaN barrier is formed by low-damage recess etching using the Cl2 plasma process. A radiofrequency (RF) power supply can accurately control the etching rate of AlGaN in GaN-based HEMTs.16,17 In this structure with 3-nm recess height, the recess etch rate in the NBE gate recess process is controlled to 5 nm/min, corresponding to RF bias power.15

The electrical characteristics of both devices (with recessed and non-recessed gate) are extracted by solving a two-dimensional (2D) drift–diffusion model. The activated models are the self-heating model to enable heat flow simulation, the ni Fermi model to include the effects of Fermi statistics into the calculation of the intrinsic concentration in expressions for the Shockley–Read–Hall (SRH) recombination, the polarization model for automatic calculation of the interface charge due to spontaneous and piezoelectric polarization, the strain model for automatic calculation of the strain from the lattice mismatch, and the impact ionization model. Furthermore, the charge at the AlGaN–GaN interface is fixed and the donor and acceptor traps at the GaN buffer are activated. Moreover, it is considered that there are no trapped charges at the interfaces between the GaN buffer layer and sapphire substrate. Table I lists the parameter values adopted in the simulations.

Table I Material parameters used in both GaN HEMT devices simulations; data from Refs. 18,19,20,21,22.
Full size table

To validate this work, the simulation results and experimental data10 for the ID–VG transfer and ID–VD characteristics for both structures, viz. the non-recessed and recessed-gate GaN HEMTs, are compared. The match obtained between the simulation results and experimental data confirms the accuracy of the model for use in further research.

Figure 2a and b show the simulated and measured10 transfer characteristics of the GaN HEMT for the non-recessed design and with a 3-nm gate recess, respectively. Figure 3a and b show a perfect match of the simulation of the direct-current (DC) characteristics with experimental results10 for different gate voltages, further verifying the accuracy of the physical models used for the GaN HEMTs. The calculated and measured data for both the non-recessed and recessed-gate GaN HEMT are presented in Table II. The maximum drain current (ID-max) is calculated to be around 444 mA/mm and 372 mA/mm for the non-recessed and recessed-gate structure, respectively, at VG = +2 V, while Vth for the non-recessed gate structure is obtained as −2.3 V versus −1.6 V for the recessed-gate structure. For the 3-nm gate recess, Vth shifts significantly, while there is a minor reduction in ID-max and gm.

Fig. 2
figure 2

Transfer characteristics of (a) non-recessed and (b) 3-nm recessed-gate GaN HEMT with VD of 5 V, AlGaN thickness (d) of 15.6 nm, and Al mole fraction (x) of  0.27. (Experimental data from Ref. 10).

Full size image
Fig. 3
figure 3

ID–VD characteristics of (a) non-recessed and (b) 3-nm recessed-gate GaN HEMT. (Experimental data from Ref. 10).

Full size image
Table II Comparison of experimental data from literature10 and simulation results for GaN HEMT devices with non-recessed and 3-nm recessed-gate structure; ns calculated for equilibrium condition, and ID-max calculated at VG = 2 V.
Full size table

The reduction in the current density for gate-recessed devices has been attributed to the diminution of the polarization sheet charge. Moreover, the 2DEG charge density (ns) is calculated while there is no voltage. The overlapping curves and equal parameters for the non-recessed and recessed-gate GaN HEMT structures confirm that the applied model exactly describes the physical phenomenon for both structures.

Results and Discussion

Model Description for Non-recessed GaN HEMT

A physics-based analytical model for the non-recessed gate GaN HEMT is presented to calculate the 2DEG charge concentration depending on the AlGaN barrier thickness.

Figure 4a depicts the band diagram of the GaN HEMT, and Fig. 4b shows the charge distribution profile, illustrating the formation of the 2DEG with electrons supplied by surface donor states. It is assumed that a high density of surface donor states exists at an energy level of Ed in the forbidden gap, measured relative to the conduction-band minimum of the AlGaN surface.

Fig. 4
figure 4

(a) Energy-band diagram of AlGaN/GaN heterostructure. (b) Charge distribution at different interfaces, and formation of 2DEG with electrons supplied by surface donor states.

Full size image

This model is based on the charge-neutrality condition across the barrier layer, where the unintentional doping of GaN and AlGaN is assumed to be negligible. Polarization in combination with the distributed surface donor states is the mechanism responsible for the 2DEG charge. By considering Fig. 4, the 2DEG charge concentration (qns) can be obtained by maintaining charge neutrality

$$ qn_{{\text{s}}} = \frac{{\varepsilon_{{{\text{AlGaN}}}} }}{d}\left[ {\frac{{\sigma_{{{\text{AlGaN}}}} d}}{{\varepsilon_{{{\text{AlGaN}}}} }} - \varphi_{{\text{b}}} - \frac{{E_{{\text{F}}} }}{q} + \frac{{\Delta E_{{\text{C}}} }}{q}} \right], $$
(1)

where EF is the difference between the Fermi level and the conduction-band minimum (CBM) in the GaN at the heterointerface, d is the AlGaN barrier thickness, and ɛAlGaN is the permittivity of the barrier layer.20

$$ \varepsilon_{{{\text{AlGaN}}}} = 10.4 - 0.3x, $$
(2)

and \(\varphi_{{\text{b}}}\) is the Schottky barrier height, which can be calculated by assuming a constant surface donor state on the AlGaN surface, n0, at a donor energy level Ed:18

$$ q\varphi_{{\text{b}}} = \frac{{n_{{\text{s}}} }}{{n_{{\text{o}}} }} + E_{{\text{d}}}. $$
(3)

Ed and n0 are linearly related to the Al mole fraction (x) in the AlGaN barrier layer.19

$$ n_{0} = (2.9x - 0.0893) \times 10^{13} \;{\text{cm}}^{ - 2} \,{\text{eV}}^{ - 1} $$
(4)
$$ E_{{\text{d}}} = 2x + 0.42\,{\text{eV}} $$
(5)

The energy band offset, ΔEC, can be calculated from the bandgap energy of AlGaN and GaN as shown in the following equation, where the bandgap of AlGaN can be measured by20

$$ \Delta E_{{\text{C}}} = 0.7\left( {E_{{\text{g}}} (x) - E_{{\text{g}}} (0)} \right) $$
(6)
$$ E_{{\text{g}}} (x) = xE_{{\text{g}}} ({\text{AlN}}) + (1 - x)E_{\text{g}} ({\text{GaN}}) - x(1 - x){\text{ eV}} $$
(7)

The polarization charge density (σAlGaN) is modeled by using spontaneous and piezoelectric polarization coefficients, which are functions of the mole fraction, AlGaN thickness, and lattice parameters of the GaN wurtzite crystal structure.

$$ \sigma (x) = \left| {2S_{{\text{r}}} \frac{a(0) - a(x)}{{a(x)}}\left\{ {e_{31} (x) - e_{33} (x)\frac{{C_{13} (x)}}{{C_{33} (x)}}} \right\} + P_{{{\text{sp}}}} (x) - P_{{{\text{sp}}}} (0)} \right|, $$
(8)

where \(a\) is the equilibrium value of the lattice constant, e31 and e33 are piezoelectric coefficients, C13 and C33 are elastic constants, and Psp is the spontaneous polarization-induced sheet charge. All these parameters are listed as functions of the Al mole fraction in the AlxGaN1−x layer in Table III.

Table III Mole fraction-dependent parameters of AlGaN/GaN heterostructure; data from Ref. 21.
Full size table

Sr is a term to account for the residual strain induced in the layer, which is calculated based on the equation23

$$ S_{{\text{r}}} = S_{{{\text{cr}}}} {\text{exp}}\left( {1 - \frac{d}{{d_{{{\text{cr}}}} }}} \right), $$
(9)

where \(d_{{{\text{cr}}}} = \varepsilon_{{{\text{AlGaN}}}} (E_{{\text{d}}} - \Delta E_{{\text{c}}} )/q\sigma_{{{\text{pz}}}}\) is the critical thickness for the onset of significant charge at the interface and Scr is the critical strain extracted from Ref. 23.

Figure 5 calculates the 2DEG charge density for the GaN HEMT with respect to the AlGaN barrier layer thickness and Al mole fraction in the barrier layer. At low barrier thickness, the piezoelectric polarization component is dominant. However, when d is substantially larger than the critical thickness (here 20 nm), only the spontaneous polarization remains. This demonstrates that the total strain-induced polarization is reduced by increasing the barrier layer thickness d. At thicknesses higher than dcr (d≫ dcr), due to the decrease in the residual strain, the piezoelectric polarization becomes zero and the 2DEG reaches an almost constant value. These modeling results match with the report by Bykhovski et al.24

Fig. 5
figure 5

Contour plot of 2DEG charge density for GaN HEMT as a function of barrier layer thickness (d) and Al mole fraction in the barrier layer. Experimental data indicated by black dots.21,25,26,27,28,29,30,31

Full size image

Moreover, AlGaN has a smaller lattice constant than GaN. So, by increasing the Al mole fraction in AlGaN, the mismatch and strain effects on the piezoelectric and spontaneous polarization gradually increase. Hence, the 2DEG charge density at the AlGaN–GaN interface increases. In addition to physical justifications, this model is verified by the quite satisfactory agreement with experimental data in Fig. 5.

Model Description for Recessed-Gate GaN HEMT

In recessed-gate structures, the barrier thickness under the gate decreases. Due to the constant electric field in the barrier layer, Ed moves away from the Fermi level and prevents the surface donor states from donating electrons to form 2DEG charge carriers at the AlGaN–GaN interface.

In recessed-gate GaN HEMT structures, to maintain charge neutrality, the electric field across the barrier layer is given below, where h is the recess height in these structures (Fig. 1):

$$ \frac{{\sigma_{{{\text{AlGaN}}}} - qn_{{\text{s}}} }}{{\varepsilon_{{{\text{AlGaN}}}} }} = \frac{{q\varphi_{{\text{b}}} + E_{{\text{F}}} - \Delta E_{{\text{C}}} }}{q(d - h)}. $$
(10)

The 2DEG electron density for the recessed-gate GaN HEMT structures can be calculated by applying Eqs. 1 and 3 to Eq. 10 and solving for the 2DEG charge density.

$$ qn_{{\text{s}}} = \frac{{\sigma_{{{\text{AlGaN}}}} h + k_{1} }}{{h + k_{2} }}, $$
(11)

where

$$ k_{1} = \frac{{\varepsilon_{{{\text{AlGaN}}}} }}{q}\left[ {E_{{\text{d}}} + E_{{\text{F}}} - \Delta E_{{\text{C}}} } \right] - d\sigma_{{{\text{AlGaN}}}}, $$
(12)
$$ k_{2} = - \left[ {d + \frac{{\varepsilon_{{{\text{AlGaN}}}} }}{{q^{2} n_{o} }}} \right]. $$
(13)

From Eq. 11 it can be seen that, by increasing the recess height, the 2DEG charge density will be decreased and the transistor starts to operate in E-mode. For a sufficient recess height to ensure that the GaN device demonstrates normally-OFF operation (h ≈ d), the critical 2DEG charge density can be calculated from Eqs. 11–13:

$$ n_{{\text{s}}} \approx \, n_{{\text{o}}} (E_{{\text{d}}} + E_{{\text{f}}} - \Delta E_{{\text{c}}} ). $$
(14)

Therefore, according to the proposed model, the ns value for the experimental recessed-gate device with an Al mole fraction of 0.27 in the AlGaN barrier layer is calculated to be 0.48 × 1013 cm−2. Figure 6 shows the 2DEG charge density modeled for the recessed-gate GaN HEMT structure with various AlGaN barrier thicknesses (d).

Fig. 6
figure 6

The 2DEG charge density of the recessed-gate GaN HEMT structures versus the recess height for various barrier thicknesses. The critical recess height is determined by the vertical dashed line.

Full size image

In this figure, the critical recess height is indicated by a vertical dashed line, at which the charge density equals ns = 0.48 × 1013 cm−2. Moreover, the accuracy of the current model is confirmed by the simulation results. Figure 7 shows the transfer characteristics of the AlGaN/GaN HEMT for various recess heights with an AlGaN thickness of d = 15.6 nm and Al mole fraction of x = 0.27.

Fig. 7
figure 7

Simulated DC transfer characteristics of AlGaN/GaN HEMT for various recess heights for AlGaN thickness (d) of 15.6 nm and Al mole fraction (x) of 0.27.

Full size image

This figure indicates that the critical recess height for this experimental device would be hcr ≈ 10 nm, where Vth = 0 V and the device will be normally-OFF. Comparison of Figs. 6 and 7 confirms that the simulation results are in good agreement with the analytical model.

The critical recess height in a GaN structure to convert it to a normally-OFF device depends on the Al mole fraction and the thickness of the barrier layer, as well as the energy level of donor states in the barrier layer. Since the recess height exceeds the critical recess height, the device converts to a normally-OFF AlGaN/GaN device.

Figure 8 graphically illustrates the band energy for various recess heights (h) and the resulting 2DEG charge density. The critical height h = hcr is the recess height at which ns can be approximated to be very small, and the device can be considered as normally-OFF or in E-mode operation. This model shows how the 2DEG charge density can be controlled by varying the barrier thickness and recess height. It could help researchers develop new approaches for E-mode GaN HEMT technology.

Fig. 8
figure 8

Band diagrams of AlGaN/GaN HEMT for various recess heights (hcr > h2 > h1).

Full size image

Conclusions

GaN HEMTs with non-recessed and recessed-gate structures are investigated, achieving excellent agreement between the simulation results and experimental measurements. Moreover, an analytical model is provided for the 2DEG charge density of the GaN HEMTs with both structures. The importance of this model is that the optimized AlGaN layers can be designed regarding the thickness, the Al mole fraction, and the recess height to control the 2DEG charge density. Achieving a high 2DEG density is a critical priority to design reliable low-resistivity high-performance GaN HEMTs.

Moreover, the model can predict the experimental observations for recessed-gate GaN HEMTs in an analytical manner, while considering the effects of the mole fraction and recess height of the AlGaN barrier layer. A relation is developed between the recess height and 2DEG charge density and can be used to extract the critical recess height at which the device converts to normally-OFF operation. The model shows excellent agreement with experimentally measured data.