Experimental and Numerical Study of C Electromigration in Iron During Ferrite-to-Austenite Transformation

Abstract

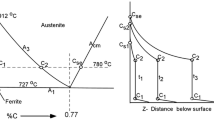
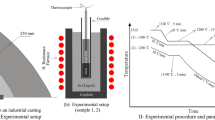
The influence of the electric current on the diffusion of carbon in an ARMCO iron sample is studied. The sample, placed between two graphite punches, is heated in the intercritical domain (between 736 °C and 912 °C) thanks to Joule heating. The diffusion of C in ferrite induces its transformation into austenite. After cooling, the microstructure of the sample gives information on the transformation fronts positions and C concentration profiles. The transformation front velocity is higher in the direction of the electric current and lower in the opposite direction. To understand and predict this phenomenon, a new model accounting both for the allotropic phase change and the electromigration of C in iron is proposed. Some model parameters are fitted comparing the predicted and the measured interface positions. With these parameters, the simulated C concentration profile is in good agreement with the experimental one.

Appendix: Discretization of the Differential Diffusion Equation Accounting for the Phase Change and Electrostatic Effect

The equation to be solved is Eq. [10] which is recalled below, rename A1 here

$$ \frac{{\partial C\left( {x,t} \right)}}{\partial t} = \frac{\partial }{\partial x}\left( {D\left( x \right)\frac{{\partial C\left( {x,t} \right)}}{\partial x}} \right) + \frac{\partial }{\partial x}\left( {\frac{{C\left( {x,t} \right)D\left( x \right)}}{RT}\frac{{\partial \mu^{0} }}{\partial x}} \right) + \frac{\partial }{\partial x}\left( {\frac{{C\left( {x,t} \right)D\left( x \right)F}}{RT}\frac{{\partial \left( {Z^{*} \left( x \right)\Phi \left( {x,t} \right)} \right)}}{\partial x}} \right) $$

(A1)

Equation [A1] is discretized considering the discretization scheme below at each node i:

For the left-hand side of Eq. [A1] a first order time discretization scheme is used:

$$ \left( {\frac{\partial C}{{\partial t}}} \right)_{i} = \frac{{C_{i}^{t + \Delta t} - C_{i}^{t} }}{\Delta t} $$

(A2)

In the first term of the right hand-side of Eq. [A1]:

$$ \left( {\frac{\partial }{\partial x}\left( {D\frac{\partial C}{{\partial x}}} \right)} \right)_{i} = \frac{{\left( {D\frac{\partial C}{{\partial x}}} \right)_{i + 1/2} - \left( {D\frac{\partial C}{{\partial x}}} \right)_{i - 1/2} }}{\Delta x} $$

(A3)

$$ \left( {D\frac{\partial C}{{\partial x}}} \right)_{i + 1/2} = D_{i} \left. {\frac{\partial C}{{\partial x}}} \right|_{{i + \frac{1}{2}}} = D_{i} \frac{{C_{i + 1} - C_{i} }}{\Delta x} $$

(A4)

$$ \left( {D\frac{\partial C}{{\partial x}}} \right)_{i - 1/2} = D_{i} \left. {\frac{\partial C}{{\partial x}}} \right|_{{i - \frac{1}{2}}} = D_{i} \frac{{C_{i} - C_{i - 1} }}{\Delta x} $$

(A5)

In this term, the concentrations are evaluated at time $t + \Delta t$ (implicit scheme) while the diffusion coefficient is calculated explicitly (at time $t$).

The discretization of the second term of the right-hand side in Eq. [A1]:

$$ \left( {\frac{\partial }{\partial x}\left( {\frac{CD}{{RT}}\frac{{\partial \mu^{0} }}{\partial x}} \right)} \right)_{i} = \frac{{\left( {CD\frac{{\partial \mu^{0} }}{\partial x}} \right)_{i + 1/2} - \left( {CD\frac{{\partial \mu^{0} }}{\partial x}} \right)_{i - 1/2} }}{RT\Delta x} $$

(A6)

with

$$ \left. {\frac{{\partial \mu^{0} }}{\partial x}} \right|_{{i + \frac{1}{2}}} = \frac{{\mu_{i + 1}^{0} - \mu_{i}^{0} }}{\Delta x}\quad \left. {\frac{{\partial \mu^{0} }}{\partial x}} \right|_{{i - \frac{1}{2}}} = \frac{{\mu_{i}^{0} - \mu_{i - 1}^{0} }}{\Delta x} $$

(A7)

and

$$ \left. {CD} \right|_{{i + \frac{1}{2}}} = \frac{{C_{i} D_{i} + C_{i + 1} D_{i + 1} }}{2}\quad \left. {CD} \right|_{{i - \frac{1}{2}}} = \frac{{C_{i} D_{i} + C_{i - 1} D_{i - 1} }}{2} $$

(A8)

In Eqs. [A11] and [A12], the concentrations C are evaluated at time $t + \Delta t$ (implicit scheme) and all the other parameters are evaluated at time t.

And for the last term of Eq. [A1]:

$$ \left( {\frac{\partial }{\partial x}\left( {\frac{CDF}{{RT}}\frac{{\partial \left( {Z^{*} {\Phi }} \right)}}{\partial x}} \right)} \right)_{i} = F\frac{{\left( {CD\frac{{\partial \left( {Z^{*} {\Phi }} \right)}}{\partial x}} \right)_{i + 1/2} - \left( {CD\frac{{\partial \left( {Z^{*} {\Phi }} \right)}}{\partial x}} \right)_{i - 1/2} }}{RT\Delta x} $$

(A9)

with

$$ \left. {F\frac{{\partial \left( {Z^{*} \phi } \right)}}{\partial x}} \right|_{{i + \frac{1}{2}}} = F\frac{{Z_{i + 1}^{*} \phi_{i + 1} - Z_{i}^{*} \phi_{i} }}{\Delta x} \left. {F\frac{{\partial \left( {Z^{*} \phi } \right)}}{\partial x}} \right|_{{i - \frac{1}{2}}} = F\frac{{Z_{i}^{*} \phi_{i} - Z_{i - 1}^{*} \phi_{i - 1} }}{\Delta x} $$

(A10)

The products CD are calculated with Eq. [A8].

Equations [A1] through [A10] are discretized equations, which are implicit for the concentration. They lead to a tridiagonal matrix system solved using Thomas’s Algorithm^[25] which is quite efficient from a computational point of view. As for every discretization scheme, the time step and space step are chosen small enough such that the results do not depend on their specific values. The space step is fixed and equal to 1 µm during the whole simulation. The time scale has to be varied during the simulation from small increment (µs) during the initial stages of the simulation to much larger one (100 s) at the end of the simulation. The value of the time step actually depends on the phase change front kinetic.

Two issues have to be discussed for the evaluation of the electrostatic potential at each node i and each time t:

• The first one is related to the time step. The electrostatic potential is link to the instantaneous electric current density. As explained in Section III, the electric current is pulsed at a frequency of 667 Hz. Considering this frequency, the use of the instantaneous value of the electric current density to describe electromigration would lead to huge computational duration. So, we assume that a continuous current density given rise to the same Joule effect (same electron matter interactions) than the pulse current density has the same influence on electromigration. This continuous current is actually the rms value of the instantaneous current. We checked a posteriori that the results are the same (not significantly different, considering numerical resolution) using the instantaneous value of the electric current and it rms value.

Equation [5] is then rewritten as

$$ - \frac{\partial \phi \left( x \right)}{{\partial x}} = \rho \left( x \right)j_{\text{rms}} $$

(A11)

• The calculation of $\phi_{i}$ is done integrating equation [A11] with the following discretization scheme:

  $$ \phi_{i + 1} = \phi_{i} - \frac{{\rho_{i + 1} + \rho_{i} }}{2}\Delta xj_{\text{rms}} $$

  (A12)