Introduction

The blast furnace (BF) is a counter-current chemical reactor producing pig iron from iron ores. Despite being responsible for the majority of the CO2 emissions from the steel industry, the BF process has remained predominant. Around 70 pct of the world’s steel is produced by the blast furnace—basic oxygen furnace route.[1] This prevalence is due to the high productivity and cost-effectiveness of the BF and its ability to yield hot metal for the production of high-grade steel.

However, the looming threat of global warming has made the reduction of greenhouse gas emissions a political and societal priority. The steel industry which contributes by around 7 pct of the global human-induced CO2 emissions,[1,2] is coming under increased pressure to reduce its environmental impact. As the main emitter of this industry, the BF process is of particular interest. Between 1950 and 1990 the coke consumption in the BF was divided by more than two,[3] halving the process CO2 emissions. Unfortunately, traditional BFs are currently running near their thermodynamic optimum. To make further CO2 savings, fundamental changes in the process are therefore needed. To solve this issue, innovative CO2 reducing technologies for BFs reaching net-zero steel have been proposed. For instance, Paul Wurth has developed a concept so-called EASyMelt™ (Electrically Assisted SYngas sMELter). The concept consists of a simulated BF process with injection of hydrogenous gases at shaft and tuyere levels, a plasma torch to superheat the gases and a liquefaction unit for CO2 capture. These elements can achieve net-zero carbon emission in a step-wise approach. Improving tuyere condition with enhanced H2 load can be the first step toward implementation of the full concept.

Enhancing the H2 utilization in the furnace is a promising approach to reduce the CO2 emissions of the BF. Hydrogen can indeed be used to reduce iron oxides, only producing H2O as a by-product. This strategy is currently a trending topic in iron-making research, with multiple review papers recently published on the subject.[4,5] In particular, the injection of hydrogen-rich gas, such as natural gas (NG), coke oven gas (COG), reformed coke oven gas (RCOG) and/or pure H2 is seen as a means to reduce CO2 emissions. NG injection is already widely implemented in Russia, Ukraine and North America.[6] However, due to NG scarcity and high cost, broader adoption is difficult. COG and RCOG injection are promising approaches that take advantage of the surplus of steel plant off-gases and have recently been the subject of a lot of interest. The off-gases are currently mainly utilized for heating and generation of electricity with low efficiency. In the framework of the Japanese COURSE50 project, COG and RCOG injection were tested in an experimental blast furnace.[7] Injection of a moderate amount of COG in the bosh was successfully implemented in two BFs of Dillinger in Germany[8] and a BF of ArcelorMittal in Spain.[9] Pure hydrogen injection also offers a significant CO2 mitigation potential. An obstacle to the implementation of the approach is the availability and price of hydrogen and especially green hydrogen. But if the so-called hydrogen-economy emerges, it would be a promising route for the production of cleaner steel. Tests of pure hydrogen injection in one tuyere of an industrial BF were carried out by ThyssenKrupp Steel in Duisburg, Germany with promising results.[10]

Due to restrictions on the minimum top gas temperature and maximum oxygen content in the blast, the amount of hydrogenous gases that can be injected at the bosh level is limited. Implementing a parallel injection in the shaft could help overcome this limitation and increase the hydrogen use in the BF. Various research projects have therefore included shaft injection as part of their strategies such as ULCOS[11] or COURSE50.[7] A parallel level of injection is also seen as a promising approach to achieve other CO2 saving technologies, such as the so-called oxygen blast furnace (OBF).[12] In this research paper, the focus will remain on bosh injection of hydrogenous-rich gas while simultaneous injection of hydrogenous gas into the bosh and the shaft will be investigated in an upcoming study.

Injection of hydrogen-rich gas in the bosh only requires small modifications of existing plants and could therefore be implemented at a relatively low cost. Yet, the injection of H2-rich gas in tuyeres has still not been widely implemented, partly due to a lack of understanding of its impact on the process and furnace’s internal state. Running tests on experimental and industrial furnaces is a useful approach to acquiring the required knowledge, but the trials are expensive and only a limited number of parameters can be tested. Furthermore, due to the very hostile environment inside the furnace, it is difficult to measure the inner state. Numerical modeling is therefore of particular interest as it can quickly and safely test a wide range of operating conditions at a low cost. It can also give a detailed view of the internal conditions of the BF.

A wide range of numerical models have been developed to study the BF performance and internal state, see References 13 and 14 for comprehensive reviews. The different models can be divided into discrete- or continuum-based approaches, depending on how the solid phase is treated. The discrete-based approach, typically represented by the discrete element method (DEM), treats every particle of the BF granular bed individually and can therefore more accurately describe the true motion of the particle bed. It can provide deep insight into complex phenomena such as softening and melting of the packed bed,[15,16] particle size distribution[17] or burden descent in the furnace.[18] However, due to a high computational cost, this method is not yet applicable to full-scale simulations and process optimization. Instead, by treating the solid phase as a fluid without considering particle interactions, the continuum-based approach can cut down computational cost considerably. Together with sub-models for the coupling between phases, chemical reactions, burden distribution and raceway conditions, this approach has been proven to accurately capture the internal state of the furnace. Continuum-based models developed have generally been for the steady state and using a 2D asymmetric computational domain for computational efficiency. In earlier attempts, the coke and ore were considered as mixed,[19] or the chemical reactions were not considered in their respective layers.[20] More recently a full layered approach has been preferred in order to more accurately describe the gas distribution and thermal state of the furnace.[21,22,23]

The injection of hydrogenous gas into the tuyere of the BF has been the subject of various numerical investigations. Wang et al.[24] studied a BF process with COG injection and top gas recycling. With tuyere COG injection a potential carbon emission reduction of 6.5 pct was predicted. Li et al.[25] studied the optimal top burden distribution for a BF process with COG injection. Liu et al.[26] investigated the impact of combining COG with hot burden charging to improve the process state. The injection of pure H2 was shown to be coupled with a decrease of the top gas temperature and pressure drop over the furnace.[27,28] Through a life cycle assessment, Tang et al.[28] demonstrated the benefit of the approach when considering environmental impact and CO2 emissions. The possibility of an unstable process under high rates of H2 or H2-NG injection was demonstrated by Okosun et al.[29] This instability is due to the quenching effect of H2 on the flame temperature which needs to be addressed. In a comprehensive study of tuyere-level hydrogen injection, Li et al.[30] showed the existence of an optimal hydrogen usage at 33.3 pct of the bosh gas content. The injection of other hydrogen rich gas has also been investigated. Liu et al.[31] studied the impact of oxygen enrichment combined with injection of off-gas from the COREX process, showing the potential of this gas to help realize the OBF. Numerical investigations have also focused on the impact of hydrogenous gas injection on the raceway conditions.[32,33,34] Despite these studies, to the best of the present authors’ knowledge, a comprehensive investigation on the impact of the injection of different hydrogenous gases on the BF process has not been presented.

A new blast furnace model, the BFinner model, has recently been developed. Its main aim is to investigate and support the implementation of a variety of CO2 emission mitigation technologies. So far, only preliminary results of the model were presented by Baniasadi et al.[35] In this paper, BFinner is described and validated using operation data. The model is then applied to evaluate the impact of various types of hydrogenous gas injection on the furnace’s internal state and overall performance. A particular focus has been given to maximizing the reduction of the CO2 emissions while still maintaining a stable process.

Model Description

To simulate the internal state of a blast furnace, a 2D axisymmetric steady-state mathematical model has been developed using the C++ programming language. The model considers the flow, heat transfer and chemical reactions for both gas and solid phases. In order to save computational time, the liquid flow was not directly solved but, its impact on the chemical and thermal state of the furnace was still accounted for. The computational domain goes from the stockline level in the throat down to the liquid surface in the hearth. The gas phase is considered as a mixture of CO, CO2, H2, H2O and N2 while the solid phase is either ore composed of Fe2O3, Fe3O4, FeO, Fe and gangue or coke composed of C and ash.

Governing Equations

The governing equations implemented for the gas and solid phases are presented in Table I. Ergun’s equation is used to describe the gas flow. This equation for packed beds has been proven to yield a similar result as when solving the full Navier–Stokes equations[21,36] and avoids the strong coupling between pressure and velocity, which requires much more computational effort. Similar to Yang et al.,[20] the coefficients \(E_1\) and \(E_2\) of Ergun’s equation where taken as 150 and 1.75, respectively. For the solid descent velocity, a potential flow model is used. Standard heat and mass conservation equations are then solved, considering the exchanges between phases and the effect of the chemical reactions. The gas density is determined using the ideal gas law.

Table I Governing Equations for Solid and Gas Phases
Full size table

Chemical Reactions

The key chemical reactions considered in the model are presented in Table II. A three-interface shrinking core model is used to describe the indirect reduction of iron oxides by CO and H2 (R0–R5). The solution loss (R6), water–gas (R10), water–gas shift (R11), water vaporization (R13) and melting (R7–R9) reactions are also included in the model. Since the liquid phase flow is not considered, an approach similar to that of Tang et al.[37,38] was adopted for the direct reduction of FeO (R12). All melted FeO was taken to transform into Fe by direct reduction in a narrow region below the bottom of the cohesive zone (CZ). The heat of reactions was either described by a constant value or as a function of the solid temperature with the expression and coefficients presented in Reference 39. Reactions involving solid components only occur in the layer where the said components can be found. For example, the melting of Fe occurs exclusively in the ore layers while the water–gas reaction is restricted to the coke layers.

Table II Chemical Reactions Considered in the Model
Full size table

Heat Transfers and Thermal Properties

The heat transfer between gas and solid was calculated based on a convective expression with the heat transfer coefficient given by the Ranz–Marshall correlation[45]

$$\begin{aligned} h = c \text {Nu} \frac{\lambda _g}{d_{\rm p}}, \end{aligned}$$
(1)
$$\begin{aligned} \text {Nu}= & {} 2+0.6\left( \text {Pr}^{\frac{1}{3}}9\text {Re}^{\frac{1}{2}}\right) . \end{aligned}$$
(2)

A corrective factor c was implemented to account for the effect of liquids in the lower part of the furnace that is hampering gas-solid heat exchanges as proposed by Hatano et al.[46] The use of such a term for the heat transfer between gas and solid has been widely implemented in the literature.[22,36] The specific area surface \(A_{\rm g-s}\) is given by

$$\begin{aligned} A_{\rm g-s} = \frac{6(1-\epsilon )}{\Phi d_{\rm p}}. \end{aligned}$$
(3)

The heat exchange with the liquid phase was simplified as a source term appearing in the gas and solid energy balance equations. This approach is based on the assumption that the liquid created in the CZ is at the solid temperature at the bottom of the CZ and will heat up to the hot metal temperature as it reaches the slag surface. This approach is similar to what was proposed by Tang et al.,[37] and the total amount of heat needed to heat up all the liquid is given by

$$\begin{aligned} Q_{\rm l,DZ} & = \sum _i^{\rm CZ} (R_7 M_{\rm Fe} + R_8 M_{\text{FeO}} + R_9 M_{\rm slag})\\ & \quad Cp_l(T_{\rm HM}-T_{\rm s})V_{\rm cell}. \end{aligned}$$
(4)

This amount of heat is taken from the dripping zone, taking into account the solid temperature effect on the heat exchange with the liquid phase. Regions with a higher solid temperature transfer more heat to the liquid than the regions where the solid temperature is lower.

The heat loss through the wall of the BF was given as a constant heat flux depending on the region of the BF considered, with highest losses in the bosh. The values taken were estimated based on the conditions for the reference BF process and correspond to a total loss of 82, 000 MJ/h (288 MJ/tHM). Physico-thermal properties for gas and solid used in the model are presented in Table III.

Table III Physico-thermal Properties Used in the BF Model
Full size table

Cohesive Zone Treatment

The CZ is the region of the BF where the solid iron ore starts softening and then melts to finally become liquid. This is a crucial region since the CZ profile affects the gas distribution and through this the thermal and chemical efficiency of the BF. Since the permeability of the CZ is affected differently by softening and melting, the CZ is generally decomposed into a softening and a melting region. In the softening zone, the porosity of the ore layers was taken to decrease from the value applied in the lumpy zone down to the value of 0.07 assumed in the melting region. The porosity was considered unchanged in the coke layers. For the melting region, a constant porosity of 0.07 was considered in the ore layers to account for the presence of the liquid mixture of Fe, FeO and slag. This value is in range to what what used by other authors such as Yang et al.[20] which used 0.1 for the ore layers in the softening and melting regions. In the coke layers, the porosity from the shaft was slightly reduced to account for liquid dripping through that layer. In order to determine the boundaries of the softening and melting regions, a criterion based on the solid temperature is set. Most earlier models used fixed isotherms of solid temperature as the boundaries of the CZ regardless of material properties.[22,48] This may be an acceptable assumption when considering a conventional BF process. However, with a high hydrogen content in the gas, the reduction degree is expected to increase, which may have a large impact on the temperature intervals at which softening and melting occurs. In the current model, for every point of the BF radius, the temperature boundaries of the two regions are set depending on the maximum reduction degree reached at that given longitudinal position. The data from Pan et al.[49] is used to derive the relation between the reduction degree and the temperature of CZ boundaries.

Grid, Numerical Methods and Convergence

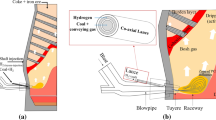
The computational domain was divided into a rectangular uniform structured grid of 10x10 cm cells which was found to give near grid-independent results. The volume calculation is based on a circular rotation of 360 deg divided by the number of tuyeres of the BF. An illustration of the domain considered is presented in Figure 1(a). The stagnant region (deadman) and raceway were preset while the dripping zone and CZ boundaries are updated during the simulation as detailed in Section II–D.

The governing equations were discretized using the finite volume method. The penta-diagonal matrices obtained are solved using the Tri-Diagonal Matrix Algorithm (TDMA)[50] known for its low computational cost. The solution procedure is illustrated in the flowchart of Figure 1(b). An overall heat and mass balance sub-model and a cellular automaton charging sub-model are first run to get the raceway conditions and the burden distribution in the furnace. Both sub-models have been extensively used and verified in an industrial setting as part of the BFxpert® system[51]. It can be noted that to obtain the raceway conditions, it is assumed that the combustion in the raceway is at a stage where only CO, H2 and N2 are coming out from it The fields are then initialized either from guessed values or from the results of the previous simulation. The solid flow is solved first using the top solid velocity calculated from the production rate and the charged material Fe content. Following that, the gas velocity and temperature fields for both phases are calculated. The chemical reactions are then updated and the compositions of the phases are computed. These steps are repeated until a rough convergence is reached. At this point, the CZ location is updated based on the solid temperature and reduction degree. A loop, similar to the one that was just described but with the update of the CZ is then applied until a convergence criterion is reached. To determine convergence, normalized global residuals are computed for the temperature fields[50]. Rough convergence is considered reached once these residuals are below \(5\times 10^{-4}\), ensuring stability when the CZ is updated. Then the final convergence is attained once the gas and solid temperature residuals are below \(10^{-4}\), at which point the simulated state remains virtually unchanged between iterations. In order to reach such a convergence, a relaxation of the energy and mass equations for both phases had to be implemented. To determine the input and output parameters, the model uses velocity boundary conditions for the solid and pressure boundary conditions for the gas. The inlet pressure of the gas is updated during the simulation to match the gas bosh volume found by the overall heat and mass balance sub-model.

Fig. 1
figure 1

BFinner model: (a) computational domain and (b) flowchart

Full size image

Optimization and Computational Cost

Since the model is aimed toward process optimization and industrial applications, the computational cost is of paramount importance. The choices not to solve the liquid flow, to use a Poisson-type equation for gas flow and a 2D domain were all made to lower the computation time. Nevertheless, further time saving by introducing more simplifications concerning the physic of the BF process are difficult to make without a significant loss in accuracy. In order to further cut time, the model was modified to run in parallel and benefit from multi-core processor capabilities. In particular, for solving the partial differential equation using TDMA, the computational domain is distributed evenly between the chosen number of processors and solved in parallel using the capabilities of the message-passing interface (MPI) library.

When running the model on a standard laptop using eight cores, the computation time to reach convergence was found to be about 15 minutes for a grid with 15,900 cells, which must be considered short. For comparison, Abhale et al.[23] reported reaching convergence in 4 hours 30 minutes on four processors for a grid of 12,300 cells.

Results

Model Validation for Conventional Operation

The BF ironmaking process is complex and a validation of the BFinner model is needed to ensure its applicability. Validation is often made difficult by the scarcity of operational data on the internal state of the furnace. In the present study, operational data for a stable period was obtained from the Rogesa blast furnace 5 operated by Dillinger in Dillingen, Germany. The company has already started its path toward decarbonization by implementing a moderate amount of COG injection. The period was considered stable since operating conditions, such as the blast flow rate and production rate stayed nearly constant. Table IV lists the operating conditions of the BF during the period while Table V gives inputs for the calculation, including the raceway conditions and material properties. The raceway conditions were obtained from an overall heat and mass balance model of the process. For the ore properties, even though both sinter and pellet were used, only the mixed properties are considered.

Table IV Operating Conditions for Rogesa BF5 Used for the Simulation
Full size table
Table V Input Parameters for Simulation
Full size table

The first metric used for validation is the top gas composition and temperature. These values are key performance indicators of the BF. Table VI shows that the predicted top gas thermal and chemical behavior are in very good agreement with the operation data.

Table VI Comparison Between Predicted and Operational Conditions for Rogesa BF5
Full size table

For a more thorough validation, in-burden probe measurements taken 5.5 m below the stock line were considered. In Figure 2, the predicted gas composition and temperature along the BF radius are plotted together with the 6 measurements taken at regular intervals during the five days of the stable period. The scattering of the operation data gives an idea of the variations of the BF process in a stable state. Overall a reasonable agreement is seen between the calculated and measured data. However, for Figs. 2(a) through (c), some discrepancies are found for the first two meters of the furnace radius even if the main trends are still well captured. These discrepancies may be due to difficulty in reproducing the burden distribution in the center, where the burden volumes involved are low and where particle segregation is expected to be stronger. Nevertheless, these first two meters represent less than 15 pct of the total furnace volume and good agreement with measurements was found for the rest of the radius. Figure 2(b) shows that the maximum CO content is found at the BF center due to the coke central charging. When moving towards the wall CO decreases but a slight increase can be observed close to the wall, likely due to the charging of nut coke in this region. As expected an opposite trend is found for CO2. For the hydrogen behavior (Figure 2(d)), a larger scattering of the measurements is observed. This may be partly related to problems in analyzing the H2 content accurately. Considering this scattering, the predicted H2 can be deemed well captured by the model.

Fig. 2
figure 2

Comparison of in-burden measurements along the radius of the BF with predicted behavior for: (a) gas temperature, (b) CO, (c) CO2 and (d) H2

Full size image

Figure 3 shows the predicted (line) and measured (squares) pressure at the wall of the BF from the stock-line level to the start of the coke active zone, showing a good agreement Furthermore, based on the predicted pressure drop in the bosh, the increase of the pressure gradient in the CZ due to the softening and melting of ore has also been well described.

Fig. 3
figure 3

Comparison of predicted and measured pressure at the wall of the blast furnace

Full size image

To illustrate the generic features of the BFinner model, a second state of the BF was simulated, corresponding to a day with a lower production due to a lower injection rate at the tuyeres. Such a process state is not desirable but the aim is to give confidence in the model’s ability to capture different BF states. Table VII presents the operating conditions and input parameters that were modified.

Table VII Modified Operating Conditions for Rogesa BF5 Used for the Simulation of State with Lower Production
Full size table

The predicted and measured top gas conditions presented in Table VIII also show good agreement with less than 2 pct difference for nearly all quantities considered. Only the H2 content of the top shows a slightly higher relative error. When considering the scattering of the measurements shown in Figure 2(d) this relative error can be deemed acceptable. Overall these results give confidence that the model is capable of capturing the BF process even under different states.

Table VIII Comparison Between Predicted and Operational Conditions for Rogesa BF5 Process with Low Production
Full size table

The thorough validation carried out in this study shows that the numerical model is capable of accurately capturing a BF process. The impact of COG, NG and hydrogen injection through the tuyere on the internal state of the BF is investigated in Section III–B. This will be done by taking the current process with high production as a basis.

Impact of Hydrogenous Gases Injection in the Tuyere

Operating conditions

The different scenarios of hydrogenous gas injection tested in this study are presented in Table IX. They were obtained from the current process by increasing the injection rate of coke oven gas (I-COG), natural gas (I-NG) or pure hydrogen (I-H2) . As shown in Table VI, these gases are not heated before the injection.

The quenching effect of hydrogenous gas injection on the flame temperature has been widely reported.[29,52,53,54] Indeed, the H2 present in the hydrogenous gas is rapidly combusted, generating vapour. Due to the high temperature conditions, this vapour is favoring the endothermic coke gasification in the raceway. Furthermore, the oxygen consumed by burning H2 reduces the oxygen availability for the strongly exothermic coke combustion. The energy needed for heating of hydrogen is also considerable, since its has a specific heat capacity of about 15 kJ kg-1K-1. For NG and COG injection, the very endothermic cracking reaction of CH4 is also partially responsible for the decrease in flame temperature.

However, PC cannot be well combusted at low flame temperatures. It is still, for now, desirable to keep PCI due to its lower cost when compared to coke. Increasing oxygen enrichment in the case of hydrogenous gas injection can maintain flame temperature and ensure proper PC combustion, but will cause a decrease in top gas temperature as less blast is required. In order to maintain a feasible and safe process, the two main operating constraints are, therefore, flame and top gas temperature.[54] In this study, the hydrogenous gas rates were increased while ensuring that the flame temperature is at least 2420K (2150 °C) and the top gas temperature is at least 363 K (90 °C). Indeed, if the top gas temperature is under the dew point, liquid water would condense at the top of the furnace which would be detrimental for the BF process. In the current process, the dew point at the furnace top is expected to be around 343 K, which is based on saturation vapour pressure described in Baehr.[55] For more safety and to limit the condensation caused by a locally lower gas temperature close to the solid particles, a security margin of 20K was added.

The production and PCI rates were kept constant to allow for a quantitative comparison of the results. Furthermore, it was assumed that the hot metal temperature remains the same for the different scenarios at 1753 K (1500 °C). Table IX shows that the coke savings are largest for NG, intermediate for COG and smallest for H2 injection.

Table IX Operating Conditions for Current and Proposed Scenarios
Full size table

In order to make the predictions more realistic, the charging model was deployed to adjust the burden distributions of the different scenarios with expected lower coke rates. These coke rates are predicted by the overall heat and mass balance model. The differences in burden distributions are illustrated by the volumic coke share in the burden along the BF radius shown in Figure 4. It can be seen that the same charging strategy was applied for all scenarios, with only the volumic coke share decreasing with intensified H2-rich gas injection. The bosh gas volume and composition for the different scenarios are presented in Figure 5. Slight changes of the bosh gas volume can be seen, this is required to ensure a constant production for the different scenarios.

Fig. 4
figure 4

Radial variation of volumic coke share in the burden for current, I-COG, I-NG and I-H2 processes

Full size image
Fig. 5
figure 5

Bosh gas volume and composition for current, I-COG, I-NG and I-H2 processes

Full size image

Effects of hydrogenous gas injection

As a good indicator of the global performance of the furnace, the top gas conditions predicted by BFinner for the different hydrogenous gas injections are presented in Table X. The H2 content in top gas is seen to reflect the composition of the bosh gas. From industrial practice, it is known that the upper limit on top hydrogen content for a current Bell Less Top charging system (BLT®) is around 13 pct when using a secondary equalizing system with N2 injection. This operating restriction is found to be respected for all the scenarios presented. For the H2 and CO utilization, small variations are observed for the different scenarios. They are due to the competition between indirect reduction by CO and H2 that depends on the gas composition and thermal state of the furnace. Furthermore, increasing the H2 content was found to favor the forward water gas shift reaction (WGSR), which has a significant impact on \(\eta _{\text {H}_2}\) and \(\eta _{\rm CO}\). Nevertheless, as was raised by Li et al.,[30] more experimental studies are needed to get an accurate model of WGSR, especially when considering high H2 content. Using the current reaction model presented in Table II, a decrease in \(\eta _{\text {H}_2}\) was found for all cases. This shows that the improvement of indirect reduction by H2 due to the hydrogen-enriched environment is not enough to fully compensate for the greater amount of H2 injected in the furnace and the faster regeneration of H2 caused by the enhanced forward WGSR. When it comes to \(\eta _{\rm CO}\) no clear trend could be observed. For the top gas temperature, a decrease is found for all new scenarios and is one of the main factors limiting higher injection rates. This is due to the higher amount of O2 needed to reach the desired flame temperature which is limiting the blast volume and therefore the heat input.

Table X Comparison of Predicted Top Gas Conditions for Current and New Processes
Full size table

The impact of the different scenarios on how the iron oxides are reduced is another good indicator of the furnace state. Figure 6 presents how the reduction is divided between indirect reduction by CO, by H2 and direct reduction. These results were obtained by multiplying the reaction rates by the volume of the cells for every cell of the computational domain. When increasing the rate of hydrogenous gas injection, the atmosphere is richer in CO and H2 and the reduction degree is expected to be higher at the CZ. This is indeed the case as shown by the lower fraction of direct reduction for all three new processes. The competition between indirect reduction by CO and H2 is well illustrated by Figure 6. The fraction of indirect reaction by H2 is found to steadily increase with the H2 content in bosh gas. However, the portion of indirect reduction by CO is significantly lower for the new processes, despite the CO content in the bosh gas being higher for all of them. Even when considering the slightly lower bosh gas volumes of the new scenarios, the amount of CO entering the BF is higher for all of them. This decreasing trend can therefore only be due to the increased competition between indirect reduction by H2 and CO.

Fig. 6
figure 6

Reduction of iron oxides for current, I-COG, I-NG and I-H2 processes

Full size image

The amount of coke consumed by water gas, solution loss and direct reduction reactions are shown for the different scenarios in Figure 7. To give a meaningful comparison of the intensity of these reactions on the coke particles in the furnace, the coke consumption was normalized by the overall coke rate of the different processes. The consumption proportion of direct reduction reaction was found to decrease with hydrogenous gas injection, which is in agreement with findings from other authors.[25,30] For the coke consumption ratio from the water gas reaction, virtually constant values were found for the different processes. Similarly, only small changes in the percentage of coke consumed by solution loss were found. Solution loss and water gas reactions are of special interest as they happen in the layered burden of the furnace and tend to decrease coke strength. If the deterioration of coke is too severe, coke of better quality is needed to ensure proper bed permeability and process efficiency.[56] This is not desirable as increasing coke quality comes at a considerable cost. For the current cases, only minor changes in the normalized coke consumption by R6 and R10 were found. A requirement of a better quality of coke is, therefore, not expected for all three hydrogen-rich gas tested.

Fig. 7
figure 7

Coke consumption from R6, R10 and R12 for the different processes

Full size image

Although global performance indicators are useful tools for providing an insight into the BF behavior, analysis of the internal state of the furnace is needed to understand the impact of the different injection scenarios. Figure 8 shows the gas temperature for the states studied and gives a good overview of a BF thermal state. The gas is injected at the tuyere level and reaches the maximum temperature in the raceway due to the combustion of auxiliary fuels and coke. In the dripping zone, the gas temperature decreases due to the endothermic direct reduction (R10) and the heat transfer to the liquid and coke. From the bottom of the CZ to the stock-line level, the gas temperature decreases at a changing rate depending on the intensity of the convective heat flow from gas to solid and the thermal impact of the chemical reactions. The gas temperature is found to be low for a significant portion of the wall region of the upper part of the BF which is in agreement with the in-burden measurements (Figure 2). This behavior is caused by the evaporation of burden moisture and the lower amount of energy available in this region, due to the lower gas flow rate caused by the high ore-to-coke ratio. For all the new injection scenarios, the gas temperature trend is similar to the current process, but with slightly lower temperatures in the upper part of the furnace. Indeed, the new processes have lower bosh gas volumes and coke rates but maintain the same production rate. Furthermore, the partial replacement of indirect reduction by CO in favor of indirect reduction by H2 also lowers the furnace internal temperature. Indeed, the reduction of wüstite by H2 is an endothermic reaction while its reduction by CO is exothermic. When it comes to magnetite, hydrogen reduction is more endothermic than carbon monoxide reduction. Finally, hematite reduced by CO releases a significant amount of heat while the reduction by H2 will, depending on temperature, release or consume a small amount of heat. A comprehensive view of the thermal impact of these reactions on the furnace has been presented by Donskoi et al.[39]

Fig. 8
figure 8

Gas temperature contours for current current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

Figure 9 shows the gas flow and CZ profiles for the different scenarios tested. The ascending gases present similar trends: they enter the BF through the tuyeres and flow upwards until they reach the bottom of the CZ. The gases are then forced to go through the coke layers due to the low porosity of the ore layers. Once above the CZ, the permeability of the ore layers is far greater and the gases return to an ascending trajectory. When considering the lower part of the BF, a region with lower gas velocity can be observed, corresponding to the deadman with its low permeability. A “center charging” program was applied so the volumic coke share is higher at the center of the BF yielding a higher permeability and a higher gas velocity. As shown in Figure 4, the volumic coke share is lower along the whole BF radius for the three new processes, reflecting the coke rates getting smaller. This decrease is higher when getting closer to the center of the furnace, leading to a greater reduction in permeability in this area. This results in a lower height of the CZ and gas velocity when compared to the current process.

Fig. 9
figure 9

Gas velocity magnitude and CZ profile for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

Figure 10 shows the distribution of hydrogen in the BF for the different scenarios. In the deadman and most of the dripping zone, the hydrogen content remains constant and equal that of the bosh gas. In these regions, no chemical reactions affecting the H2 content occur. In the upper part of the dripping zone, a slight change in the hydrogen volume fraction is observed and is caused by the production of CO by the direct reduction (R12). The H2 content of the gas then steadily decreases during the ascent, primarily due to the indirect reduction by H2. However, some H2 can be regenerated by the forward WGSR. The greater impact of the WGSR for higher H2 content can be observed when comparing I-H2 to the current process, the regeneration of H2 by WGSR being more intense for I-H2. It is especially obvious in the upper part of the furnace belly, close to the wall. Higher hydrogen content in bosh gas is seen to be linked with higher H2 content in the whole furnace, despite the increased indirect reduction by hydrogen. The distribution of H2 along the radius is found to reflect the distribution of coke in the BF. Indeed the higher H2 content is found at the center where the volumic coke share is maximal as shown in Figure 4. The hydrogen content then steadily decreases along the radius, with a slight reversal of the trend close to the wall since nut coke was charged in that region.

Fig. 10
figure 10

Hydrogen content for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

The contours of the WGSR rate are shown in Figure 11. This reaction can proceed in both directions in the BF depending on the ratio between \(y_{\rm CO}y_{\text {H}_2\text {O}}\) and \(y_{\text {CO}_2}y_{\text {H}_2}\). Nogami et al.[27] reported that the regeneration of H2 and generation of CO2 increase with the injection of hydrogen in the furnace. This behavior is also found here with the forward WGSR being enhanced by a higher hydrogen content, while the backward reaction is decreasing.

Fig. 11
figure 11

Water-gas shift reaction rate for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

For a more in-depth understanding of the behavior of H2 in the furnace, Figure 12 presents the reaction rate contours of indirect reduction by H2. Various factors such as particle size, gas flow rate or H2/CO ratio are affecting the kinetics of H2 reduction reactions. Nevertheless, \(\eta _{\text {H}_2}\) and temperature are widely regarded as the two main parameters, with an equilibrium diagram often plotted from them to give an insight into the reduction behavior.[57] For the current scenarios, in the top meters of the furnace, no indirect reduction takes place as the temperature is too low. Once the solid temperature is high enough, hematite starts to be reduced to magnetite by H2 and, directly after this, magnetite is reduced into wüstite. Yet, the main utilization of H2 is for the reduction of wüstite to Fe, which is agreement with what has been presented in the literature.[25,30] The greater proportion of indirect reduction by H2 when the H2 load increases is clearly seen in Figure 12 and can be observed for all the concerned reactions (R1, R3 and R5).

Fig. 12
figure 12

Indirect reduction rates by H2 for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

The H2 utilization is also given in Figure 13. It can clearly be seen that despite the higher amount of indirect reduction by H2 and forward WGSR, the \(\eta _{\text {H}_2}\) stays lower for the scenarios with increased hydrogen content. As discussed previously, this can be attributed to the greater amount of hydrogen introduced into the system, which counterbalances the aforementioned effects.

Fig. 13
figure 13

Indirect reduction rates by H2 for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

Figure 14 depicts the contours of CO gas utilization in the BF for the different scenarios tested. Similar trends are found but some slight differences in values can be observed. Below the CZ, no CO is consumed but only generated by R12. The CO utilization then steadily increases as the gas ascends in the furnace due to the indirect reduction by CO. The CO utilization at the center is lowest for the case in Figure 14(a) and highest in Figure 14(c), largely reflecting the effect of the coke rate on the burden distribution as discussed above.

Fig. 14
figure 14

CO gas utilization for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

Figure 15 shows the reduction degree of solid iron oxides for the different scenarios, demonstrating the effect of hydrogenous gas injection. The expected behavior can be observed for all cases simulated, with iron oxides getting reduced as they travel down in the furnace and reaching their maximum reduction degree at the CZ bottom. The reduction is then completed in the dripping zone with liquid FeO being reduced to liquid Fe by the direct reduction mechanism (R12). Despite the fact that the H2 bearing gas injection lowers the gas temperature in the upper part of the BF, as shown in Figure 8, the reduction of iron oxides occurs at a higher height in the furnace for the new scenarios. This is due to the higher reducing power of the gas injected in the BF with a higher CO and H2 content. Similarly, this is why the reduction degree reached at the CZ bottom is minimum for the current process and maximum for I-NG.

Fig. 15
figure 15

Reduction degree of solid ferrous oxides for current (a), I-COG (b), I-NG (c) and I-H2 (d) processes

Full size image

To get a view of the environmental impact of the different hydrogenous gas injection cases, a simple estimation of the CO2 emissions for the different scenarios was carried out. This estimation is focused on the BF process and based on the assumption that all the carbon introduced in the BF through the reducing agents will ultimately be transformed into CO2. COG is not considered as it is an internal gas which was produced by coke ovens and is reused in the furnace. Its emissions are therefore attributed to the coking and not the BF process. This holds true if COG can be replaced by green electricity in the reheating furnace and power plant. Table XI presents the estimated CO2 emissions compared to the emissions of a conventional BF process without any hydrogenous gas injection. It appears that due to a high carbon content, NG has the lowest positive impact on CO2 emissions with higher emissions than the current process with moderate COG injection. On the other hand, COG and pure H2 could both allow for a significant decrease in the CO2 emissions of the furnace. NG could, however, be useful for reforming CO2 of blast furnace gas into H2 and CO. This reformed gas could then be injected in the BF shaft, which is a promising technology for further emission savings.

Table XI Predicted CO2 Emissions for the Different BF Processes
Full size table

Conclusions

Maximizing hydrogenous gas injection into the tuyere of the BF is a promising approach to mitigate the environmental impact of the process without revamping the furnace. A deep understanding of the effect of the injection on the overall performance and internal state of the furnace is however needed before the concept can be brought to industrial application. With this objective, a mathematical model of the BF has been presented and validated using operational data of a blast furnace currently operating with a moderate injection of COG. With the accuracy and resilience of the model proven, the injection of different hydrogenous gases (NG, COG and pure H2) has been tested at the maximum rate where a safe and stable process can be maintained. The major findings of the study are:

  • With a higher hydrogenous gas injection, the three indirect reduction reactions by H2 are enhanced, partially replacing the indirect reduction reactions by CO and the direct reduction.

  • Due to a lower blast volume higher oxygen enrichment and the endothermic indirect reduction by H2, intensified hydrogenous gas injection is coupled with a decrease of the top gas temperature. This is a limiting factor for further increasing the injection rate.

  • Decrease in temperature is coupled with a lowering of the CZ height in the BF, slightly modifying the distribution of gas in the furnace.

  • Overall, the impact of COG, NG and pure H2 injection on the internal state of the process is rather similar. From a technical point of view it seems that all three approaches could therefore be implemented and the choice depends on fuel availability and cost of operation.

  • COG and pure H2 injection in the tuyere show a potential to reduce the CO2 emissions by respectively around 8 and 6 pct compared to those of conventional BF process. However, due to its high C content, NG can only marginally reduce the emissions of the process.

COG and/or pure H2 injection at the tuyere level are therefore attractive approaches to mitigate the environmental impact of the BF. Injection of these fuels does not require any significant modification of the steel plant and can be implemented at a moderate cost. Nevertheless, CO2 emissions savings of 8 pct are still not enough to meet environmental targets. More intense injection could yield further savings, but are likely not possible as the top gas temperature must be kept above the dew point and the flame temperature cannot go below a given threshold for good PC combustion. To achieve further savings, innovative technology such as a parallel injection in the shaft of the BF or the use of plasma torches to heat the injected gas are required. The present model will be a useful tool to assess the impact of such approaches on the BF process and facilitate their industrial application.