Investigations on Vibrational Interpretations of Bubbles in Metal-Making Processes

Abstract

Vibration measurements were carried out using highly sensitive accelerometers in an experimental ladle integrated into the LIMMCAST (Liquid Metal Model for Steel Casting) facility at HZDR. The model is operated with liquid Sn–40 wt pctBi alloy at 200 °C, whose physical properties are close to those of molten steel. Three accelerometers were attached to the outer wall of the LIMMCAST vessel to record the vibrations caused by the argon bubble flow in the liquid metal at different process parameters. The results obtained at the liquid metal experiments differ from those reported for water models where the relationship between root mean square (RMS) value of the vibration amplitude and the gas flow rate follows different curve shapes. Furthermore, the results of vibration measurements in the LIMMCAST model are compared with vibration measurements in a steel plant during vacuum degassing. The comparison of the RMS data shows a fairly good agreement. This indicates that the vibrations in both the industrial process and the laboratory model are caused by the same physical mechanisms, and thus, the vibration behavior in an industrial steelmaking ladle can be reproduced quite well by suitable liquid metal models. These studies on bubble flows can help to improve the understanding of industrial stirring processes and thus contribute to a better process control.

Introduction

Gas injection is nowadays a common procedure leading to more intense stirring, enhanced mixing conditions, and higher process efficiency in the ferrous and nonferrous industry.^[1] In melting processes of aluminum scrap, for example, for hydrogen removal, gas stirring is essential for the production of high-quality aluminum castings.^[2] The efficiency of refining processes is increased by injecting gas while achieving a homogeneous dispersion of a large number of bubbles into the liquid bath, where the generated bubbles promote degassing and inclusion removal in molten aluminum.^[3] In copper smelting, oxygen gas is injected into the furnace, leading to smelting and slagging reactions for the production of high-quality matte. Mixing as a result of gas injection also plays an important role with respect to the efficiency of smelting processes.^[4] Furthermore, in the copper industry, reduction of oxygen takes place in reactors where natural gas is added below the surface of the liquid until the desired level of oxygen in the molten copper has been achieved. In secondary steelmaking, gases are broadly used during ladle treatment and degassing as well as during decarburization processes. In ladle metallurgy, inert gas stirring is essential for the homogenization of the steel bath, desulphurization, degassing, and inclusion removal. In contrast to the great importance of gas stirring for metallurgical technologies, the monitoring and control of the respective processes have so far been based mainly on observations of phenomena on the free surface of the liquid bath.^[5,6]

Measuring systems are yet to be developed for accurate control and optimization of gas stirring processes; for example, the control of the gas flow rate into the ladle. In most cases, gases are injected into the ladle through bottom plugs, but can also be injected through top blowing lances or side plugs. The control of the amount of gas fed in by the operators is often limited to the displays of the gas regulators that are part of the central gas supply system. These regulators are placed rather far from the plugs which means that the measurement system is exposed to the risk of pipe leakage. In other cases, flowmeters are installed at the gas pipelines for monitoring the adjusted value of the flow rate but even this approach cannot eliminate false recordings in the pipeline or blockages of the plugs.^[5,7] If the gas losses lead to a lower gas feed in the ladle, a lower stirring intensity will be achieved there. However, any uncontrolled increase of the gas injection into the ladle to counterbalance the gas loss might result in overcompensated stirring and can cause problems such as damage of the vessel lining and slag entrapment.^[8] This can cause significant problems in the processes and can impair the quality of the end product. Therefore, it is necessary to improve the control of the gas flow during the injection process and the current state of the flow in the ladle. In case of high-intensity stirring, observations at the free surface flow with an infrared (IR) camera can potentially give an indication of the stirring intensity by monitoring the size of the formed slag-free open metal surface (open eye).^[9] However, this approach to controlling the stirring process by means of an IR camera is not feasible in the case of soft stirring, as the IR camera is not able to detect the escape of gas bubbles from the surface of the ladle. But even in the case of high gas flow rates, the method is not free of problems. The irregular shape of the open eye is very difficult to determine in the case of strong disturbances of the free surfaces as in the case of the vacuum degassing. In addition, the relationship between the characteristics of the open eye and the flow structures in the volume and the efficiency of the stirring process is not clear. Thus, the use of an IR camera in ladles during both soft and heavy stirring provides only rough information about the dynamics of the stirring and the process flow. However, combining this measurement technique with vibration measurements presented in this study could have the potential to improve the accuracy of the process analysis.^[10,11]

As shown in the past, there is a high potential of using vibration measurements as a diagnostic tool for the gas stirring process in industrial metallurgy. Significant efforts to control ladle treatment and vacuum degassing processes with the help of vibration measurements have been carried out both in laboratory-scale experiments and in industry by using accelerometers. Accelerometers can be implemented in investigations for interaction between gases and liquids and provide us with information regarding stirring conditions.^[12] When inert gas is injected into a liquid through plugs, the gas rises because of the lower density and leads to formation of gas bubbles and bubble plumes. Bubble oscillation, bubble–bubble interaction, such as coalescence, or fluid–structure interaction cause vibrations and sound.^[13,14] During gas injection, dynamic turbulences are generated by the rising bubbles and result in ladle wall vibrations. Capturing such vibrations can give us information regarding the behavior of the bubbles in the liquid. Accelerometers mounted on different vertical and horizontal positions can capture vibrations which may contain information regarding the phenomena occurring at the nearby position.^[15] As mentioned in previous work, when using vibration measurements for metallurgical purposes and investigations, the amount and quality of information are not affected by the location of the sensor.^[5] Thus, vibration measurements in the industry can be vital, since an opportunity is offered to obtain data from the process and its real-time performance. In the harsh industrial environment, however, vibration measurements are a major challenge. Although accelerometers are relatively robust and can withstand relatively harsh conditions, high operating temperature will always be a limiting factor. The temperatures can be significantly high near the target system i.e., at ladle treatment stations. Accelerometers also prove to be advantageous for industrial measurements because they can be mounted on cooler surfaces a few meters away from the measurement object rather than onto the ladle wall and still provide high-quality measurement signals.^[5]

Previous laboratory studies with water models have been employed for interpretation of vibration signals for experimental investigations of fluid flow and related transport phenomena processes.^{[5,6,7,10,16]} Burty et al.^[7] studied vibration measurements both on laboratory models using water as modeling fluid and on industrial setups. Based on the measurements the authors were able to establish a correlation between the gas flow rate and the vibration levels captured by accelerometers. Yenus et al.^[5,6] related the flow rate range to the frequency range in which the sensors were forced to vibrate. Xu et al.^[11] also proved that the analysis of vibration signals enables the monitoring of the ladle treatment. As shown in their investigation of a water model, the vibration signal varies between 1 and 120 Hz and in general, the magnitude of the vibrations increases with the gas flow rate. The root mean square (RMS) of the obtained vibration signal is another parameter that increases with growing gas flow rate.^[14] The importance of the RMS value was examined by Alia et al.^[15] in experiments using water as modeling liquid. The authors obtained useful insights regarding the information content and quality of measuring signals obtained from sensors at different locations around the model. Based on that, the authors proposed guidelines for an optimized vibration-based ladle stirring control. An extensive work related to process control using vibration signals during ladle treatment has been conducted in the framework of a European project.^[10] In this work, vibration measurements were performed in water models in ambient atmosphere and as well as under vacuum conditions. Results showed a direct relationship between the vibration signals and process parameters as a function of gas flow rate, water depth, and number of stirring plugs. The findings demonstrate that the level of vibrations is affected by multiple experimental and design parameters.^[10] The amount of research on this topic shows the need for the introduction of a sound measuring technique to control the gas agitation process control, with Pylvänäinen et al.^[17,18] highlighting the imperative of controlling the intensity of gas stirring to ensure high productivity and quality of the produced material. This work emphasizes the importance of indirect measurements, such as vibration measurements, during vacuum degassing at the SSAB, Raahe, Finland. The study revealed that gas stirring process control by means of vibration sensors can be well achieved and gas leakages can be more easily detected. In conclusion, vibration measurements can contribute to the development of online monitoring systems for gas stirring processes and identify irregularities of the gas flow. Burty et al.^[7] performed industrial measurements and revealed the potential of vibration measurements for stirring control during ladle treatment. A relationship between the vibrations of the ladle and the removal rate of inclusions under the influence of gas stirring was observed.

Investigations for efficient stirring in studies on laboratory scale have been dedicated so far mainly to water models. As the gas is injected into the ladle through the plugs, a two-phase region is created, the so-called plume. The liquid around the plume is accelerated by the rising gas bubbles and follows an upward movement in which the bubbles separate at the free surface of the liquid.^[19] Diverse phenomena take place during gas injection into steelmaking vessels which can produce vibrations to be captured by the accelerometers. However, the characteristics of the bubbles such as shape, size, and velocity are significantly affected by the thermophysical properties of the liquid where the gas is injected.^[20,21,22] Srivastava et al.^[21] showed that thermophysical properties of liquids such as viscosity and surface tension affect the size of the bubbles. An increase in both values results in an increasing Sauter mean diameter of the bubbles formed.^[21,23] In addition, surface tension was found to play a greater role than viscosity in influencing the bubble size.^[21] In addition to the bubble size, the bubble shape is also strongly influenced by viscosity and the surface tension, which affects the bubble dynamics and the interaction between the gas and the liquid phase.^[20,24] Likewise, in the case of liquids with lower surface tension, it has been observed that the generated bubbles have a smaller size than in fluids with higher surface tension.^[24] Liquids with low surface tension show a higher frequency of breakup resulting in an increasing number of bubbles with smaller size.^[21] A mechanism for bubble formation is proposed by Cho et al.^[22] where surface tension plays a major role in the nucleation, expansion, and elongation of the bubbles. Previous work has demonstrated that hydrodynamics and surface tension can affect the phenomena of bubbles coalescence during bubble rise. Studies by Kostetskii et al. reported a linkage between the surface tension of the liquid and the vibrational behavior of the studied experimental ladle in terms of RMS values.^[16] Furthermore, Keplinger et al. showed that the bubble breakup in liquid metals differs significantly from the breakup in water. While the breakup in the liquid metal results in two particular newly formed daughter bubbles, multiple daughters are formed upon breakup of a bubble in water.^[25]

Experiments using liquid low temperature metals like GaInSn,^[24,25] PbSn^[26], or SnBi^[27] for modeling are much less common than corresponding studies in water models, as their operation is often somewhat more complex and places higher demands on the measurement techniques. On the other hand, these liquid metal models are much cheaper, more flexible, and more productive than comparable tests in real industrial plants. In addition, the liquid metal experiments offer the best conditions for testing measurement techniques that are intended for use in real industrial plants. Therefore, such models are important tools for experimental investigations of flows and transport phenomena in steel making processes, since liquid metal models satisfy the similarity conditions much better than comparable water experiments due to the material properties of the liquids.^[24] In addition, these model experiments provide valuable experimental data for the validation of numerical flow simulations.^[28] In this work, vibration measurements are performed in the experimental facility LIMMCAST (Liquid Metal Model for Steel Casting) at HZDR and compared with pre-existing measurements in water models. Another part of this work is dedicated to the comparison between vibration data obtained by the LIMMCAST model and measurements conducted during vacuum degassing in a Swedish steel plant. For this purpose, vibrational data were recorded by a short-time campaign during vacuum degassing in the steel plant. In this work, an attempt was made to further close the gap between investigations of the vibrational behavior due to bubble flows in physical ladle models and in real metal-making processes. This study will further contribute to a better fundamental understanding of the vibrational behavior of bubbles in metal-making processes.

Methodology

In addition to numerical simulations, physical models are an important and legitimate tool for investigating flow and transport processes in industrial processes. However, in order to interpret their results correctly with regard to the real process, similarity considerations must be taken into account.^[14,15] Apart from the geometry, the ratios of various forces that determine the flow phenomena should be reproduced as realistically as possible. In ladles with gas injection, bubbles cause motion in the melt, which is governed by viscous, inertial, and buoyancy forces.^[29] In terms of thermophysical properties, density, viscosity, and surface tension are perceived as dominant factors influencing bubble formation and evolution. The dimensionless Morton number (Mo) is composed of these essential material properties of the fluid and the gas^[30] and determines the shape of the bubbles in the surrounding fluid. The Morton number is expressed in Eq. [1] as the ratio between viscous and surface forces,

$$ {\text{Mo}} = \frac{{g n_{{\text{L}}}^{4} }}{{\rho_{{\text{L}}}^{2} \sigma^{3} }} \Delta \rho $$

(1)

where $g$ is the acceleration of gravity; $n_{{\text{L}}}$ is the dynamic viscosity of the fluid; $\rho_{{\text{L}}}$ the density of the fluid; $\sigma$ is the surface tension of the fluid; and $\Delta \rho$ the density difference between the two phases. Usually, the Morton number in water and liquid metals differ by several orders of magnitude. The behavior of bubble rising in liquid metals at low melting temperatures has been studied in previous publications.^{[24,25,31,32]}

The LIMMCAST facility is operated with the binary alloy Sn–40 wt pctBi at a temperature of 200 °C. Its physical properties are listed in Table I along with those of water and a common industrial steel grade X5CrNi18-10 as utilized in previous studies.^[33,34] Since it is a liquid metal, the physical properties of the SnBi alloy at 200 °C are closer to those of molten steel at 1550 °C than compared to water. Consequently, the Morton number of the SnBi alloy shows that the SnBi alloy can be considered more representative of molten stainless steel than water when determining the shape of the bubbles in the surrounding fluids.

Table I Physical Properties of X5CrNi18-10, Sn–40 wt pctBi Alloy and Water

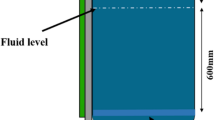
The liquid Sn–40 wt pct Bi alloy is placed in a 1:5.25 model of an 180t industrial ladle as this has been implemented in a previous study.^[27] The diameter of the experimental ladle is 600 mm, similar to the bath height. The ladle is equipped with four different possible purging plug positions on the bottom plate. The experimental setup is illustrated in Figure 1.

Fig. 1

(a) The experimental ladle containing the liquid Sn–40 wt pct Bi and (b) the outer shell of the experimental ladle indicating the positions for mounting of the accelerometers (E, G, H)

As in a previous publication,^[27] the Froude similarity is used for flow rate conversion as given in Eq. [2].

$$ Q_{{\text{M}}} = \sqrt {\frac{{\rho_{{{\text{g}},{\text{O}}}} }}{{\rho_{{{\text{g}},{\text{M}}}} }} \frac{{\rho_{{{\text{L}},{\text{M}}}} }}{{\rho_{{{\text{L}},{\text{O}}}} }} \left( {\frac{{d_{{\text{M}}} }}{{d_{{\text{O}}} }}} \right)^{5} } Q_{{\text{O}}} $$

(2)

where $\rho_{{{\text{g}},{\text{O}}}}$ is the industrial gas density; $\rho_{{{\text{g}},{\text{M}}}}$ is the density of the gas in the experimental setup; $\rho_{{{\text{L}},{\text{M}}}}$ is the density of the SnBi liquid metal at 200 °C; $\rho_{{{\text{L}},{\text{O}}}}$ is the density of the steel melt; $\frac{{d_{{\text{M}}} }}{{d_{{\text{O}}} }}$ is the scale of the model; and $Q_{{\text{O}}}$ is the industrial injection flow rate.

The initial momentum of the injected gas was neglected in the bottom gas stirred model, as justified by the fact that the momentum of the injected gas is dissipated shortly after injection and the plume is governed by the buoyancy of the rising gas as described by K. Krishnapisharody et al.^[35] As a result of the Froude similarity (Eq. [2]), the examined flow rate in the model is varied from 0.2 to 3.6 NL min⁻¹ representing gas flow rates between 12 and 216 NL min⁻¹ in the steel ladle.

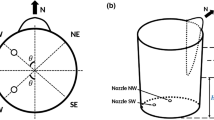
The gas flow rate was accurately controlled by a gas flow controller (MKS, model GE50A), which can supply argon with a maximum flow rate of 6.85 NL min⁻¹ (± 0.2 pct). Argon was injected into the model by two different plug types: slit plug and porous plug (see Figures 2(b) and (c)). Two different plug positions were utilized for the Argon injection into the liquid metal; one at the center and one at a radial position close to the wall of the experimental ladle (Figure 2(a)). In any of the cases investigated here, both plug positions (Figure 2(a)), equipped with the same type of plug, were utilized simultaneously for argon injection. The LIMMCAST facility provides the possibility to perform experiments both in ambient atmosphere and at low pressures to resemble the industrial process of vacuum degassing. In our setup, the ladle is equipped with a lid (Figures 1 and 2) which seals the experimental ladle. Vacuum (final pressure with gas ballast at 0.3 mbar) was produced inside the experimental ladle by employing a PFEIFFER UnoLine vacuum pump with pumping capacity of 583.33 L min⁻¹. During the experiments, the vacuum was controlled by an electronic gauge.

Fig. 2

(a) Top view sketch of the experimental ladle with marked plug positions (b) used slit plug and (c) used porous plug. Only one type of plug was used during experiments in both of the ladle plug positions

For the vibration measurements, three mono-axial accelerometers were utilized with a sensitivity of 1000 mV/g (± 5 pct sensitivity tolerance). The high value of sensitivity contributes to the quality of this work, where in such experimental investigations, high sensitivity is required to capture vibrations induced by the bubble flow during argon injection in the experimental ladle. The three sensors were mounted at three different locations (E, G, H) onto the external surface of the tank wall as shown in Figures 1 and 2. The accelerometers E and G were placed slightly above the free surface of the bath, while H was located below the free surface at 498 mm from the bottom of the ladle as shown in Figure 1. The sensor mounted at the position H (Figure 1) is more prone to vibrations of the ladle wall after bubbles generation and coalescence. The top-mounted sensors above the liquid bath (E, G) are more prone to vibrations of the structure as bubbles burst or leave the upper free surface of the liquid. A more detailed description of the accelerometers utilized in the current work as well as a description of the overall measurement equipment is given in a separate section later in the manuscript. During the operation of the ladle and vibration measurements, argon gas was injected into the ladle at specific flow rates starting from 0.2 NL min⁻¹ to 3.6 NL min⁻¹ with a step of 0.2 NL min⁻¹. After each variation of the flow rate, the system was given at least 5 minutes to settle into the new quasi-steady state before starting the vibration measurements. In particular, the root mean square (RMS) value of the obtained acceleration signal was used to characterize the system state. The RMS value in each investigated case was calculated in MatLab® provided by MathWorks.^[36] The raw signal data of acceleration from all three accelerometers (E, G, H) was stored in a PostgreSQL database after digital conversion as described more in detail in Section III. Then, the data were extracted from the PostgreSQL database and stored in discrete sets in relation to the gas flow rate. MatLab was used to calculate the RMS values as the square root of the arithmetic mean of square of the acceleration amplitude at each flow rate (Eq. [3]). For the curve fitting in the produced graphs, the Curve Fitting Tool 3.5.9 in the application toolbox was used. Although the system was responding quickly to flow rate changes, data only from the three intermediate minutes were assessed to avoid any transitional periods between different flow rate values. This has been applied to any of the investigated cases and therefore the signal for each flow rate has an onset of 60 seconds after the flow rate was adjusted by the gas flowmeters.

$$ {\text{RMS}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{n = 1}^{N} \left| {\chi_{n} } \right|^{2} } $$

(3)

where $N$ is the total number of values and $\chi_{n}$ is the acceleration amplitude.

The coefficient of determination (R²) was calculated in MatLab by means of Eq. [4].

$$ R^{2} = 1 - \frac{{{\text{SSE}}}}{{{\text{SST}}}} $$

(4)

where SSE is the sum of squared error, and SST is the sum of squared total.

The same procedure was followed for the extraction of data from the database where the signals from the industrial measurements were stored. However, in the industrial measurements, the time intervals were not the same for all flow rates, since they were determined by the steel grade and the corresponding chemical reactions. The same formulas [Eqs. 3, 4] were used for the calculation of the RMS and R² values for the vibration measurements during VD treatments in industry.

The sampling frequency of the sensor was set to 25 k Hz. It is of great importance that the data obtained are free from external vibrations, so that only the undisturbed signal can be examined for the interpretation of the flow condition. The amplitude of the signal measured when the LIMMCAST was not in operation was found to be very low. Therefore, vibrations from other sources rather than the bubble flow in the LIMMCAST facility can be considered negligible. Thus, the signal captured by the accelerometers refer to vibrations originating from the bubble flow in the ladle only.

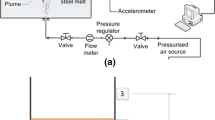
Another series of vibration measurements were performed during the actual industrial vacuum degassing process at a steel plant in Sweden. The vibration measurements during vacuum degassing (VD) presented in this work refer to a ladle with a capacity of 65 t of molten steel. Argon gas was injected into the melt through two slit plugs placed on the bottom plate of the ladle as shown in Figure 3. The argon gas was injected at varying gas flow rates up to 140 L min⁻¹ under a low pressure of 4 mbar. The flow of argon gas was controlled by a Bronkhorst flow controller with a maximum flow rate of 500 L min⁻¹ ± 0.4 pct. The vacuum was controlled with a pressure gauge.

Fig. 3

Top elevation sketch of the industrial ladle with the positions of the plugs utilized for argon gas injection during the vacuum degassing process at the steel plant

In the steel plant, the temperature in close distance and on the ladle wall is significantly high. A high-temperature environment can result in lower accuracy of the vibration measurements. Therefore, the sensors were mounted at safe distance onto steel plates which were welded onto the ladle-supporting system where the ladle is placed during VD. The generated vibrations during VD were transferred from the ladle to the ladle-supporting system and were captured by the accelerometers mounted onto it. For clarification, the placement of the accelerometers on the ladle-supporting system is presented in Figure 4. The temperature at those mounting locations was about 70 °C. The accelerometers ACC2 and ACC3 were placed at such a position to capture vibrations perpendicularly to the VD station. Vibrations to the horizontal axis and perpendicular to the studied system give the highest amplitude. The ACC1 accelerometer was more prone to background vibrations which originated from other ongoing processes and activities in the melt shop. The signal from the accelerometer ACC1 has been studied to identify the background vibration sources while vacuum degassing. Additionally, for a better understanding of the vibrations, related only to the process of interest, notes were taken during the measurements with a timestamp regarding external vibrational sources, in addition to an installed camera for recording background activities. Vibration measurements from four different VD treatments, out of 25 in total, were selected to be further investigated in detail. Only during these four VD treatments, side processes that could disturb the vibration signal such as the Electric Arc Furnace (EAF), the Ladle Furnace (LF) and the casting operation were shut off during the measurement period. In addition, the activity of the cranes causing additional vibrations around the VD station was reduced. Thus, it can be assumed that the captured vibration signals originated mainly from the ladle while vacuum degassing only. This has to be further investigated and shall be addressed and clarified in future studies. For all four measurements, the sensors were mounted at the same positions (ACC1, ACC2, and ACC3). The procedure for vibration measurements was the same for all four VD treatments presented with the use of the same measuring equipment. However, other influencing factors changed during the tests including the total mass of the liquid steel, the mass of the slag, the steel grade, and the thickness of the refractory layers. Further investigations need to be done to get a clearer picture about the impact of these factors on the vibrational signals in the industrial environment.

Fig. 4

(a) Photograph of the industrial ladle and ladle-supporting system indicating the location of the accelerometers, where vibration measurements were performed (with permission by the steel plant), (b) sketch depicting the location of the accelerometers mounted onto the ladle-supporting system during vacuum degassing

For the industrial measurements, the duration of the vacuum degassing process was around 40 minutes. Argon gas was initially injected to the industrial ladle during VD starting at low flow rates around 20 L min⁻¹ and was gradually increased to higher values, of about 250 L min⁻¹.Vacuum was applied throughout the process and the treatment was accompanied by electromagnetic stirring. Electromagnetic stirring (EMS) is considered as soft stirring for improving mixing conditions.^[37] However, the literature does not reveal the contribution of EMS to the generated vibrations during vacuum degassing. From what the authors have seen so far with regard to EMS and its contribution to the vibration signals in industry, the EMS is unlikely to have a major influence on the vibration signal. The influence of EMS on the vibrational signal is still under investigation and will be clarified in later work.

The Measuring Equipment

Vibrations can be captured and quantified by accelerometers. When using an accelerometer, several factors should be taken into consideration to ensure reliable and accurate measurements. The accelerometer should be able to capture vibrations in the frequency range the system operates. Humidity and temperature are factors that can influence the accuracy of the measurements. Another significant requirement for guaranteeing the quality of the measurements is the appropriate mounting of the device.^[38] Among magnetic, adhesive, and stud mounting, the latter is reported with the widest dynamic measurement range and it is preferred in demanding environments.^[38] It is reported that the cable length is a major aspect of the installation of vibration sensors. In general, cables have a certain capacitance, and the load increases with the length. This capacitive loading reduces high-frequency vibration signals. However, the effect of this capacitive loading for normal industrial applications where the signal is limited up to 10 kHz is not a problem for cables less than 70 m in length between the sensor and the power source.^[38]

For vibration measurements in the current study, three Wilcoxon 799 M mono-axial accelerometers were utilized with a sensitivity of 1000 mV/g (± 5 pct sensitivity tolerance), calibrated in the frequency range from 0.2 to 2500 Hz. The sampling frequency is 25 kHz. The measuring setup consisted of the accelerometers, a multiple channel analog input module, and a desktop computer. The analog signal was transmitted from the accelerometers to the analog input module through coaxial cables; one individual cable for each accelerometer. According to the conditions in these experiments, the length of the cables was chosen to be 30 m. The signal was converted to digital and sent to a desktop computer through an NI cQDAQ-9134 Ethernet chassis. On the desktop computer, Lab VIEW 2014 SP1 (64-bit) received the signal which then was stored as raw data on PostgreSQL databases. A block diagram of the measuring system applied in the LIMMCAST experiments is presented in Figure 5.

Fig. 5

Designed measuring system for vibration measurements as implemented in the LIMMCAST setup with three sensors mounted onto the external wall (ACC E, ACC G, ACC H)

Results

Measurements at the Liquid Metal Model LIMMCAST

The vibrations generated by the two-phase flow in the LIMMCAST setup were studied as a function of argon gas flow rate. For the porous plugs and the slit plugs (there were always two of the same type in operation during the measurements), the acceleration amplitude of the vibrations shows an increasing trend with the flow rate. Figure 6 shows the results of measurement conducted for the slit plugs as a function of gas flow rate. The graphs refer to the signals captured by accelerometer H, where accelerometer E and G produced similar curves (not shown here). The increase in the amplitude of the oscillations with growing gas flow rate is evident in Figure 6.

Fig. 6

Vibration signals captured by the accelerometer H for gas injection through the two bottom slit plugs operated each by the same gas flow rate, where the flow rate values given in legend indicate the total flow of both of the bottom plugs

The next step in evaluating the data provided by the accelerometers was to quantify the intensity of the vibration signals. This was done in a simple way by calculating the root mean square (RMS) value of the acceleration measured. Figures 7 and 8 show the calculated RMS values as a function of the gas flow rate, whereby the two injection positions were equipped with either the porous plugs (Figure 7) or the slit plugs (Figure 8). These measurements were carried out under the condition of ambient pressure.

Fig. 7

RMS values of acceleration for accelerometers (E, G, H) at varying gas flow rates for parallel injection through two porous bottom plugs, where the flow rates given on the x-axis indicate the total flow of both of the operated plugs

Fig. 8

RMS values of acceleration for accelerometers (E, G, H) at varying gas flow rates for parallel injection through two slit bottom plugs, where the flow rates given on the x-axis indicate the total flow of both of the operated plugs

It is interesting to note in Figure 7 that in the case of the porous plugs, we see, in the data of all three sensors, a linear dependence of the RMS values on the increasing volume flow with the same slope. This is not the case when the slit plugs are used as shown in Figure 8. At best, a linear relationship can only be deduced for small volume flows up to about 1.6 NL min⁻¹, whereby the measured values of accelerometer E show a higher gradient than those of the other two sensors. In the range between 1.6 and 3 NL min⁻¹, the increase of the RMS values slows down significantly before a stronger increase is observed again at higher gas flow rates.

Figure 9 shows the calculated RMS values vs the gas flow rate also for a gas injection through slot bottom plugs, but this time under vacuum conditions. It is apparent that there is no longer a linear relationship. The fits rather show that these curves obviously take the form of a power law.

Fig. 9

RMS values of acceleration for accelerometers (E, G, H) during Argon gas injection through two slit bottom plugs in the LIMMCAST setup under vacuum conditions as a function of flow rate, where the flow rates given on the x-axis indicate the total flow of both of the operated plugs

Measurements in the Steel Plant

Analogous measurements to those performed out at the LIMMCAST test facility were carried out at a Swedish steel plant. The industrial measurements concern the process of vacuum degassing and are thus most similar to the LIMMCAST experiments under vacuum conditions. The gas flow rate in the industrial process was varied up to about 250 NL min⁻¹. Thus, taking into account the similarity considerations as discussed in Section II (see Eq. [2]), we can state that there is a fairly good agreement between the model experiment and the real industrial plant with respect to the non-linear shapes of the curves. The RMS values of acceleration calculated from the vibration signals recorded by the accelerometers ACC 1, ACC 2, and ACC 3 during vacuum degassing are shown in Figure 10.

Fig. 10

RMS values of acceleration for a series of measurements vs gas flow rate for all installed sensors (E, G, H) in the LIMMCAST setup operated under vacuum and for vibration measurements during VD treatment in the steel plant (ACC1, ACC2, ACC3). For the industrial measurements, four different VD treatments out of 25 have been selected to be representative. For the measurements at LIMMCAST model, the figures are a replot of the data as presented in Fig. 9. The equations of the plots are presented in the legend

For direct comparison, the LIMMCAST results from Figure 9 are plotted again in Figure 10. Here, the parameter range of the gas volume flow rate was adapted according to Eq. [2]. In the industrial data, it is noticeable that the individual curves for the different VD treatments as well as for the sensors sometimes deviate very significantly from each other. We have pointed out in Section III that such deviations are to be expected due to the type of sensor installation and the difficulty of comparing the process conditions for the particular VD treatments. Therefore, we do not want to go into these issues in detail here, but rather point out that the measurement curves both in the model experiment and in the industrial process show a power law fitting.

Discussion

Measurements at the Liquid Metal Model LIMMCAST

In this study, measurements were carried out both in a steel plant and on a laboratory-scale liquid metal model over a wide range of gas flow rates as well as variations in gas injectors and pressure conditions. In general, it can be stated for all measurements carried out that the amplitude of the recorded vibrations increases steadily with increasing gas flow rate. This is to be expected if one considers that the vibration is mainly generated by the flow in the ladle. It is difficult and challenging to establish a clear and unambiguous relationship between the respective flow characteristics and the measured vibrations. The reasons for the occurrence of the vibrations can be manifold: turbulent structures in the fluid generated by the rising gas, collisions of bubbles, coalescence or breakup, the bursting of bubbles at the free surface, the formation of surface waves, etc. A definite assignment to these individual phenomena is hardly possible with the present knowledge, but all these mentioned phenomena are undoubtedly amplified with increasing gas flow rate. All these events could create local pressure fluctuations that spread through the fluid and are transmitted to the container wall where the accelerometers are installed.

The results obtained at the LIMMCAST experimental facility revealed a very interesting finding. In the case of using porous plugs for argon injection, the measured data of all three accelerometers (E, G, H) show a linear slope of the RMS values with increasing gas flow. This behavior changes when slit plugs are used, where a power law increase in the RMS values of the vibrations is observed. In view of the above discussion on the origin of the vibrations, it can be concluded from the less pronounced increment in the signal amplitudes that in the case of slit plugs, the number of bubbles and the degree of turbulence in the bath do not rise as much as in the case of gas injection through porous plugs. This general assumption is confirmed in the experimental study reported by Trummer et al.^[39] who compared the performance of porous and slit gas injectors in a water model. According to their observations, the number of gas bubbles increases only slightly with increasing volume flow in gas injection with slit plugs. In comparison, significantly more gas bubbles were detected in the case of the porous plugs. It is reasonable to assume that bubble–bubble interactions such as collisions and coalescence should occur more frequently the more gas bubbles are in the fluid. This circumstance can, but does not necessarily have to, explain the different slope of the RMS curves in the LIMMCAST experiments.

Two further aspects have to be taken into account in this regard:

• 1. It is known that water and liquid metals show a fundamentally different wetting behavior. While one can be fairly certain that the gas injectors used by Trummer et al.^[39] were completely wetted, the wetting of porous surfaces in the Sn–Bi alloy is very difficult to achieve. The formation and detachment of the individual bubbles on the gas injector is essentially determined by the wetting: X-ray visualization experiments in the ternary GaInSn alloy revealed that the bubble formation at a non-wetted gas injector reduces the number of bubbles significantly.^[25] An increase in the gas volume flow then tends to increase the bubble size. Preliminary measurements in the LIMMCAST setup using local resistivity probes for bubble detection and local void measurements indeed found only minor differences in bubble number between porous and slit plugs.^[27]

• 2. If a growing gas volume flow in case of the slit plugs does not result in a larger number of bubbles, the average bubble size will increase. It is known that large bubbles can also be an effective generator of local turbulence as they experience a greater buoyancy force and thus provide for greater local velocity gradients. At the same time, the size of the bubbles increases the tendency for pronounced oscillations in the shape of the bubbles and for bubbles to break open. Both mechanisms can certainly also be considered as a source of vibrations.

Alia et al.^[15] conducted vibration measurements in water using a vessel with a similar geometry as the LIMMCAST model. This gives us the opportunity to directly compare the results from a water experiment with the results from the LIMMCAST model, where SnBi was used as the modeling fluid. However, we have to keep in mind that the vibration signal can also be influenced by many factors, whereby the respective relationships have probably not yet been fully clarified and understood. It must also be taken into account in this comparison that, despite all similarities in terms of geometry or gas injection, the two experiments differ not only in the use of different fluids. Concerning this, it can be assumed that there are relevant differences in the details of the construction and materials of the fluid containers as well as in the mounting or the sensitivity of the accelerometers. Unfortunately, such detailed information is usually not listed in the respective papers. In the model by Alia et al.,^[15] the gas was injected through bottom purging plugs (not further specified) and the vibration signals were captured by mono-axial accelerometers located at different locations onto the outer shell of the vessel. A comparison between the liquid metal model and the results reported for the water model by Alia et al.^[15] is presented in Figure 11, where the LIMMCAST data from the Figures 7 and 8 are re-plotted here. In order to be able to compare both cases, the values of the gas volume flow rate from the LIMMCAST experiments were also adjusted here using Eq. [2]. It should be noted that the water experiments cover a smaller parameter range of the gas volume flow than LIMMCAST, so that the comparison must be restricted to the range of small gas contents. A clear difference is that the curves from the water model already follow a power law at small values of the flow rate, while the measurements in the liquid metal reveal a linear behavior. In the case of the porous plugs, the linear behavior is found over the entire parameter range studied in LIMMCAST under normal pressure, while for gas injection through the slit plugs, the linear relationship is lost at higher volumetric flow rates. Other studies^[10,16] using water models equipped with porous plugs, but different vessel geometries, show as well a power law dependence of the calculated RMS values within flow rates up to 60 L min⁻¹.

Fig. 11

RMS values of vibration measurements as a function of the gas flow rate: Comparison between results from LIMMCAST and results from water model by Alia et al.^[15] within similar gas flow range

Although Figure 11 shows obvious differences between water and liquid metal, their explanation in the vibration data is far from being straightforward. We can assume that for comparable gas volume fractions, fewer but larger bubbles are found in the liquid metal than in the water. This, of course, should have consequences on the turbulence level in the fluid as well as on frequency and intensity of bubble–bubble interactions. Unfortunately, there are only very few quantitative studies in the literature focusing on bubble–bubble interactions in liquid metals. Bubble collisions, coalescence, and breakup events were investigated by Keplinger et al.^[24] Because X-ray radiography was used in these studies to visualize the gas bubbles in the opaque liquid metal, the experiments were limited to thin geometries, making direct comparisons to water flows in large three-dimensional vessels difficult. However, as part of a special investigation to validate the measurement method, a limited set of experiments in the thin geometry with liquid metal and water was directly compared.^[40] These measurements confirm the expectation of the occurrence of larger gas bubbles in the liquid metal compared to a larger number of dispersed bubbles in water. Moreover, the bubble deformation in water has been found to be larger in water than in the liquid metal. The bubbles in liquid metals tend to have a more spherical-like shape while the bubbles in water can be described as oblate ellipsoids with a wobbling surface. The main reason for these effects is the higher surface tension of liquid metals in comparison with water. The rising velocities of the gas bubbles are found to be rather similar in both fluids. The higher buoyancy in the liquid metal is obviously compensated by the increased drag force owing to the larger bubble size. Investigations of bubble characteristics in water models have shown an overall increase in the bubble size with increasing flow rate.^[41,42,43] In addition, Srivastava et al.^[41] in their work relating the bubble size in water with different operating parameters observed that the level of the flow rate had a role in the initiation of coalescing of the bubbles as examined at different regions in the water volume. Liu et al.^[44] investigated the bubble characteristics in a water model. An increasing number and size of the bubbles were observed for gas flow rates higher than 0.5 L min⁻¹. Furthermore, the authors suggest that higher flow rates are needed, typically between 1.5 and 2.0 L min⁻¹, to initiate the collision and coalescence of bubbles.^[44]

The bubble diameter is a crucial parameter determining the dynamics of two-phase flows. An increasing bubble size raises the drag coefficient of a rising bubble. The interface also becomes increasingly susceptible to instabilities with the result that bubble oscillations set in, further increasing the flow resistance of the bubble. The bubble breaks up as soon as the local shear flow along the bubble reaches a critical value, which depends on the surface tension.^[25] Bubble oscillation and breakup should contribute to vibrations. Gao et al.^[45] reported an increasing bubble rising velocity with growing bubble accompanied by increasingly irregular deformations of the bubble surface. They considered the formation of plumes with gas bubbles of different sizes where small bubbles prefer to remain in a narrow region at the center of the plume with low slip and lift velocities, while larger bubbles tend to spread out with higher slip and lift velocities, resulting in broader plumes. This suggests higher local turbulence levels associated with increased turbulent transport for larger bubbles. In the latter case, the interaction of the plume with the ladle side wall is expected to be more intense, contributing to the increase in the vibration intensity detected by the accelerometers. Consequently, for the compared flow range, in the liquid metal, the linear increase of the RMS values may be a result of the greater oscillations produced during the rise of larger bubbles in the plume. In contrast, in water, the utilized modeling flow rates as described in the cited study^[15] are found below the threshold value required for the initiation of bubble collision and coalescence as suggested by Liu et al.^[44] In addition, below the threshold, only a slight increase is observed in the size of the bubbles with increasing flow rate whereas a gradual increase in the number of the dispersed bubbles is exhibited.^[44] Thus, a large number of small bubbles in the fluid may not be able to maintain the linearity of the increase of the RMS values, turning the trend into a power law with an exponent smaller than one. To this point, it is important to mention again that the observed differences between the compared models are restricted to the range of small gas contents as found available in Reference 15, whereas, at higher flow rates, the relationship between the RMS and the increasing flow rate in liquid metal turns to power law for argon injection through bottom slit plugs (see Figure 8). However, the current observed differences are a base for circumstantial future work to examine in detail the variations in the vibrational behavior of bubbles formed in fluids with varying physical properties.

Another part of the present study is devoted to the investigation of the vibration characteristics under vacuum conditions, as this constellation plays a crucial role in metallurgical technologies such as vacuum degassing. The LIMMCAST facility offers the possibility to perform measurements in a closed system where the air can be effectively evacuated. This provides a good basis for comparison with the situation in the industrial process. The corresponding RMS curve from the LIMMCAST in Figure 9 shows a dominant power law increase for increasing gas flow rates up to 3.6 NL min⁻¹ for all three accelerometers (E, G, H). The RMS values of acceleration reach higher values than the corresponding RMS values calculated for the LIMMCAST operated under ambient conditions. Measurements of the gas distribution by Wondrak et al.^[27] in the LIMMCAST setup in the same parameter range revealed that the number and size of bubbles increase significantly with decreasing pressure beneath the free surface of the bath. More specifically, during bubble rising under vacuum, large bubbles surrounded by an increased number of smaller bubbles are present in the flow domain. The gas from the smaller bubbles diffuses into the larger ones through a thin film prior to formation of larger bubbles.^[46] The capability of larger gas bubbles to enhance the vibration level in the ladle has already been discussed above. Another striking phenomenon is the bursting of the large gas bubbles on the surface of the bath which can be attributed to the fact that the large bubbles approach the free surface with high ascent velocity.^[27] When bubbles reach the free surface of the liquid metal bath, a large thin film dome structure is created. The bursting of the bubbles results in the dispersion of small droplets of liquid metal above the free surface.^[27] These small liquid metal droplets fall back to the liquid metal bulk. This bursting phenomenon generates surface waves that propagate toward the wall of the ladle. As a consequence, the vibration activity is intensified under vacuum conditions. Such a bursting of bubbles is not observed in corresponding experiments at ambient pressure.^[27] The gas escapes smoothly; the free surface is only marginally disturbed and therefore does not enhance the vibrational activity significantly. Bursting of bubbles in the top free surface of the liquid metal has been studied previously at the LIMMCAST model by Wondrak et al.^[27] where extreme differences in the disturbance of the top surface under vacuum were captured in photographs and videos.

The current study at the LIMMCAST model aims to give insights to the vibrational behavior of bubbles in liquid metal with physical properties close to those of molten steel. Analysis of data from measurements with other characterization techniques for bubbles combined with vibration measurements is currently conducted in liquid metal as well as in water inside exactly the same setup. The study will be presented in a later publication to reveal further information regarding the generation of the signal with respect to bubble evolution events and characteristics of bubbles such as size and velocity as well as other associated phenomena such as mass transfer.

Measurements in the Steel Plant

In the industrial trials, the accelerometers used in this study proved to be effective for measuring vibrations under such challenging conditions due to their high sensitivity. As can be seen in Figure 10, the vibration measurements in both the LIMMCAST model under vacuum and in the industrial ladle result in a power law increase of the RMS values as a function of gas flow rate.

Four VD treatments at the industrial ladle were selected to be presented in this work as explained in Section II. Figure 10 clearly shows that the RMS curves for the industrial ladle follows a power law increase for all three accelerometers used (ACC1, ACC2, ACC3) in these four VD treatments over the entire gas flow range investigated. It is worth to note that the measurements from sensor ACC1 in the industrial ladle for VD 3 and VD 4 reveal an almost constant level of the RMS values, f(Q_gas) = k with exponents in the power law being much smaller than 1. ACC1 was a background accelerometer which bears the risk that its activity can be disturbed by another background source activity (for example, passing cranes and trucks, movement of casting ingots, and other equipment) although this was not noticed during these two particular VD treatments. On the other hand, it could be that this chosen measuring position is unfavorably located for the detection of flow-induced vibrations, i.e., that it is difficult to detect the corresponding signals there owing to weak amplitudes. ACC1 was mounted on a column made of concrete, at a higher position as the other two sensors.

A growth of the RMS values of the acceleration with increasing flow rate according to a power law is also observed during the LIMMCAST measurements for all three utilized accelerometers (E, G, H) (see Figure 10). Here, the fitting of the data result in quite similar exponents of the power law. Especially for the top-mounted accelerometers (E, G), which capture vibrations mainly caused by bubble bursting at the free surface, the exponent is almost identical. For accelerometer H which was mounted below the free surface, the exponent achieves a slightly higher value. The reason for this behavior is not fully clear. It could be that the intensity of the bubble–bubble interaction in the volume increases more with increasing gas volume flow than the amplitude of the phenomena at the bath surface. In the industrial trials, on the other hand, the variance of the values of the exponent between the different sensors and VD treatments is much more pronounced, whereby the measured values of ACC2 and ACC3 are closer together. The deviation of ACC1 has already been pointed out.

ACC2 and ACC3 were mounted at the same height around the industrial ladle. Obviously, this measuring position is much more suitable for recording flow-induced vibration signals which could be used for a characterization of the stirring process.

As already mentioned in Section II, many factors such as the total mass of the liquid steel, the mass of the slag, the steel grade, and the thickness of the refractory layers are variable between the respective VD treatments, causing further uncertainties. The significantly lower deviations of the individual measurements in the LIMMCAST model are certainly due to the fact that the experimental conditions are defined there and are much easier to control. Therefore, the discrepancies between the LIMMCAST data and the measurements in the steel plant are not very surprising, as they differ in the accelerometer placement, vessel geometry, material properties, and process characteristics. However, a quantification of the various influencing variables was not carried out in this study and must be a key subject of future work.

All measurements in this study have shown very clearly that there is a direct dependence of the intensity of the vibrations on the gas flow rate. This makes vibration measurements a promising candidate for characterizing and monitoring the process of gas stirring in steel ladles. So far, the operator of the industrial process who wants to know about the status of the gas stirring is mostly limited to observations of the free surface. In particular, the injection of inert gas into liquid steel from the bottom of the ladle generates the so-called open eye forming a passage of the ascending gas through the slag, whose size, and dynamics could indicate something about the stirring intensity. However, the emergence of the open eye requires a certain minimum gas volume flow. Argon injection at low flow rates has been suggested as a stirring practice under vacuum for an interval of ~ 30 minutes to avoid events such as re-oxidation and circular flows which can reduce the efficiency of inclusions removal.^[46] However, gas injection at relatively low flow rates (10–20 L min⁻¹) does not lead to the formation of the open eye.^[46] As our work shows, accelerometers are capable of recording vibrations that can be associated with motion even at low flow rates, making vibration measurements during vacuum degassing throughout the stirring process a supportive monitoring tool even at low flow rates and soft stirring. In addition, this approach offers more comprehensive insight into the process since even in the case of an open eye, usable information about the structure and behavior of the two-phase flow inside the liquid metal, which is needed to evaluate the intensity and efficiency of the stirring process, can scarcely be obtained.

The similarities in the results obtained by the LIMMCAST model and the VD treatments in the steel plant are encouraging for continuing the investigations. However, the observed discrepancies raise a number of open questions regarding the relationship between the vibration signals and the underlying physical mechanisms. The development of a robust model for control of gas agitation based on the combination of vibration measurements in physical liquid metal models and industrial measurements is quite complicated and requires advanced signal processing and statistical techniques. In this context, the comparison of the data from the industrial process with those from the physical model is particularly important, as in the latter the boundary conditions and process parameters can be set accurately and reproducibly, thus providing a fundamental understanding of the vibration data. This is a work in progress. Further investigations of the vibration measurements are currently being carried out both in industry and at LIMMCAST. The results will be reported in later publications.

Conclusions

Concepts for the control of industrial stirring processes in steel making are created on the basis of fundamental knowledge and data obtained through physical modeling and industrial observations. In this study, to the authors' knowledge, vibration measurements were carried out for the first time on an experimental ladle operated with a liquid metal model fluid (SnBi at 200 °C).

The following conclusions result from this study:

• 1. The vibration amplitude increases with increasing gas flow rate which is obviously a consequence of the intensified turbulent motion in the liquid metal. The information obtained from the vibration measurements can be used for process monitoring, for instance, the identification of abnormal stirring conditions, e.g., in the case of a blocked stirring plug and for control of soft stirring processes with no visual observation possibilities on the top free surface of the metal bath.

• 2. Operational parameters such as type of plugs and applied pressure on the free top surface of the liquid metal bath show a significant effect on the RMS (root mean square) values of acceleration. Modification of these conditions results in variations in bubble flow characteristics, such as the number and size of the bubbles, bubble collision, coalescence, and bubble breakup events. Therefore, the influence of these parameters should be carefully investigated for developing dedicated models for process control.

• 3. The dependence of the RMS values on the gas flow rate for the measurements in LIMMCAST setup under vacuum conditions shows similarities with the corresponding curves during vacuum degassing in industry. The observed similarities strengthen the validity of the LIMMCAST measurements with respect to vibration measurements in metal-making vessels. These investigations are ongoing and will continue. Further measurements are planned and comparisons of industrial measurement data with liquid metal experiments will further improve the accuracy of models and concepts for stirring control in metal production vessels in future.

• 4. The analysis of the vibrational signals reveals the differences between vibration measurements in the LIMMCAST model and physical models where water was used as a modeling fluid. It is reasonable to assume that these deviations can be explained, at least in part, by the differences in the material properties of the fluids. However, it is difficult to establish an exact correlation, because despite the similarities of both models in terms of geometry and gas injection, there are nevertheless differences in the details of the construction and the materials of the fluid containers. The observed differences in the oscillatory behavior of the bubble flow between water and SnBi at 200 °C may have implications for deriving appropriate methods for controlling gas agitation processes in industrial vessels. It is imperative to investigate such differences in the vibration behavior of liquid metal and water in detail in order to establish sound measurement methods for controlling stirring processes in industry based on vibration measurements.

Vibration measurements in physical liquid metal models such as LIMMCAST provide an attractive tool for a comprehensive characterization of two-phase flows and bubble behavior in liquid metals and for an improved understanding of the origin and dynamics of vibrations measured at the ladle wall. The outcome of this study is encouraging for further investigations in physical liquid metal models for the establishment of a solid technique for stirring process control using accelerometers in metal-making ladles which is based both on experimental and industrial data.