Introduction

The kinetics of phase transformations plays a key role in materials science and metallurgy. In this sense, the results of sophisticated experiments to be explained by physically based models can contribute to a deeper understanding of solid/liquid phase transformations and their industrial application. For instance, the microstructural evolution of ceramics during processing determines the final phase fractions, microstructural features and is crucial for the properties of the material during operation (see, e.g., Reference 1). Furthermore, the kinetics of solid/liquid phase transformations determines the behaviour of ceramic refractories, oxide inclusions and fluxing agents in contact with metallurgical slags. Hence, understanding the kinetics is key for predicting the longevity of the refractory and improving the quality of ceramic and metallic materials.[2,3,4,5] The corrosion resistance of refractories is decisively determined by incongruent and congruent phase transformations and their different kinetics must be respected in process design.[6] A specific metallurgical application of solid/liquid phase transformations is the design of freeze linings,[7] where the microstructure of these linings is determined by the solidification rate of nonferrous slags.[8] In this context, Heulens et al.[9,10] investigated the morphology and kinetics of the isothermal crystallization of wollastonite by means of in-situ HT-CSLM. In addition, solidification modelling is a key task to enable and optimize the valorization of metallurgical slags.[11,12,13] Hence, precise knowledge of the kinetics of crystal growth and melting is required for an optimized processing of oxide systems.

Recent developments in experimental techniques in combination with mathematical modelling and numerical simulation offer new possibilities for investigating and identifying the rate determining processes of phase transformations. In this context, cyclic partial phase transformations allow to reveal the growth of a phase on the expense of another phase while nucleation processes are not expected to interfere with the growth kinetics. In addition, impingement effects present at high volume fractions are avoided, and thus, also cannot compromise the growth kinetics. In earlier works[14,15,16,17,18,19] the transformation kinetics of the austenite-to-ferrite and ferrite-to-austenite phase transformation in low alloyed steels has been investigated by means of cyclic partial phase transformations. A sketch of a typical phase transformation process is presented in Figure 1, where the fraction \(\xi ^{\alpha }\) of the new phase \(\alpha\) is plotted vs time t. During nucleation, characterized by the time interval \(t_{\text {nucl}}\), some critical nuclei of the newly formed phase become stable. In the subsequent growth stage, occurring in the time interval \(t_{\text {growth}}\), the stable nuclei grow at the expense of the old phase. It is likely that nucleation is negligible for cyclic partial phase transformations, which take place in the two-phase region only, as indicated by the green arrow in Figure 1. A proper heat treatment is required to keep both phases (e.g. austenite and ferrite) present during the experimental procedure.

In Figure 2 a typical heat treatment for cyclic partial phase transformations is presented, where both, the lower temperature \(T_1\) and the upper temperature \(T_2\) of the heat treatment cycle, remain in the two phase region. By this procedure both phases remain present during heat treatment. It is possible to exceed this temperature range between \(T_1\) and \(T_2\) by overheating or undercooling. However, in that case it must be ensured that both, the solid and the liquid phase, remain present throughout the heat treatment.

In this work, partial cyclic phase transformations are applied to study solidification and melting of oxide crystals, namely wollastonite, in liquid \(\text {CaO}\)-\(\text {SiO}_2\)-based slags. First, the temperature is raised above the liquidus temperature. Then, the samples are cooled down in the two-phase region between the solidus and the liquidus temperature. Subsequently, the temperature is cycled with both phases remaining present. Eventually, the sample is cooled down to room temperature.

Normally, nucleation and growth kinetics cannot be separated. This problem is circumvented by the method of cyclic partial phase transformations. Let us assume that a migrating interface exists in the two phase region. Then, the transformation kinetics is solely controlled by the migration of the already existing interface and is not obscured by nucleation events.

Fig. 1
figure 1

The phase fraction \(\xi ^{\alpha }\) is plotted vs time in this schematic sketch. A phase transformation typically consists of a nucleation stage with time duration \(t_{\text {nucl.}}\) and growth occurring in the time span \(t_{\text {growth}}\). The green double arrow indicates the region for the partial cyclic phase transformations (Color figure online)

Full size image

Generally, two extreme cases of phase transformation kinetics can be distinguished. In the first case, the kinetics of a phase transformation can be controlled by the diffusion of the components in the bulk material of the phases. In the second extreme case, the transformation reaction at the interface between two reacting phases is the rate limiting step of the phase transformation (see, e.g., Hillert[20]). For an arbitrary composition the melting kinetics of binary or multi-component phases is usually influenced or even controlled by diffusion of the components in the liquid. In the second case, i.e. congruent melting and solidification, chemical diffusion processes are not required; thus, the kinetics is expected to be controlled by the interfacial reaction only.

In this work, we investigate whether the simple theoretical concepts described above can be verified by experimental studies. If this is the case, then the derived models are valuable tools for predicting the kinetics of solid-liquid phase transformations with the consequence that these simple models can be used for many problems in industrial practice.

The transformation kinetics is investigated for these two different cases, namely diffusion controlled, incongruent phase transformations and interface reaction controlled, congruent phase transformations. To this aim, two different slag compositions are selected:

  • First, a bulk slag composition is chosen that differs from the wollastonite composition, where incongruent melting and solidification of wollastonite is expected to occur during cyclic heat treatment. In this case, diffusion processes are expected to take place to account for the composition differences.

  • The second composition of the slag lies in the region for a congruent phase transformation, where bulk diffusion processes are not required, so that the kinetics are expected to be interface reaction controlled.

The relevant part of the \(\text {CaO}\)-\(\text {SiO}_2\) phase diagram is shown in Figure 3. The phase diagram is calculated by means of FactSage 7.3[21] using the FToxid database. The two selected compositions of the system for the experimental observations are marked by a green line for the incongruent case and a yellow line for the congruent case, respectively.

Fig. 2
figure 2

A typical heat treatment for partial cyclic phase transformations were the temperature is cycled in the two-phase region

Full size image
Fig. 3
figure 3

Extract from the \(\text {CaO}\)–\(\text {SiO}_2\) phase diagram showing the equilibrium phases in the relevant temperature and mole fraction ranges for this work. Green line: Composition for incongruent phase transformations; yellow line: composition for congruent phase transformations (Color figure online)

Full size image

Experimental

The cyclic growth and shrinkage of wollastonite particles in \(\text {CaO}\)–\(\text {SiO}_2\) slags is observed by means of High Temperature - Confocal Scanning Laser Microscopy (HT-CSLM). The experimental setup consists of a VL2000DX CSLM from Lasertec and a high temperature furnace of the type SVF17-SP from Yonekura, also referred to as mirror furnace in the following. The gold coated furnace chamber has an ellipsoidal geometry with the sample located at one of the focal points and a heat source in the form of a halogen lamp located at the opposite focal point. A platinum crucible located on top of the sample holder contains the pre-melted sample material during the experiment. A laser beam with a wavelength of 405 nm acts as a light source. This ensures high contrast as the wavelength of the laser is well below the spectrum of the heat radiation of the sample. A sketch of the experimental set-up is shown in Figure 4.

Fig. 4
figure 4

Scheme of the HT-CSLM set-up, Chair of Ferrous Metallurgy, Montanuniversität Leoben

Full size image

One requirement for the measurement configuration is that the slags crystallise in a defined area. In addition, the slag layer has to be thin and should hardly contain any bubbles. An easily manageable sample temperature control is necessary to maintain the required cooling and heating rates for cyclic partial phase transformations. For this purpose, thermocouple wires are inserted from the side into the heating chamber of the mirror furnace via the holes of a corundum rod, see Figure 5. Beforehand, a type S thermocouple is welded together, bent over a rod and twisted behind it. The approximately circular thermocouple loop is then flattened to reduce the height. Before the test, the loop is placed flat on the bottom of the platinum crucible and the pressed slag sample is positioned on top of it. During heating, the slag melts, fills the loop and the excess slag runs off to the outside of the crucible. Due to this experimental setup, it is possible to perform the furnace control directly via the sample thermocouple and to use another thermocouple on the underside of the sample carrier as safety feedback.[22] However, the temperature distribution in the sample itself during the heat treatment may deviate from being homogeneous due to heat flows in the experimental set up. A deeper discussion on temperatures of HT-CSLM samples during heat treatment with a focus on metallic samples is given by Britt and Pistorius.[23]

Fig. 5
figure 5

Representation of the sample thermocouple in the mirror furnace without sample, see [22]

Full size image

At the beginning of the experiment the sample is heated up above the liquidus temperature to ensure that the material in the platinum crucible is in liquid state. After a cooling phase below the liquidus temperature wollastonite crystals form at the platinum wire loop where they stay present throughout the partial cyclic phase transformation. The rotation of the solid wollastonite crystals is prevented since the are connected to the immobile platinum wire.

A partial phase transformation is provoked by reheating the now already existing crystals to just above the liquidus temperature and then cooling several times in a cyclic manner. The movement of the solid/liquid front is video-recorded and evaluated using digital image analysis. In Figure 6 the moving solid (liquid) front is shown during a partial cyclic phase transformation at the incongruent slag composition. The kinetics of the phase transformation is investigated by tracking the solid/liquid interface and measuring the observable area of the solid phase during the cyclic partial phase transformations.

Fig. 6
figure 6

The solid/liquid front during a transformation cycle at 1515\(^\circ \text {C}\). In case of solidification, the solid wollastonite (bright gray) situated at the left side grows, meaning that the solid/liquid front migrates to the right. During melting the wollastonite shrinks, which is visible by a front migration to the left. The platinum wire used as the original nucleation site is also shown in this figure

Full size image

Representative results of the image analysis are shown in Figure 7(a) for a typical transformation cycle. The red zone is the frame for the observation window which consists of the white area (liquid phase) and the blue colored area (solid phase). The extension of the observation window is tantamount to the maximum solid fraction observed in this individual transformation cycle. The phase fractions of the solid and the liquid phase are presented at different times t in Figure 7(a). The snapshots from the image analysis are shown at 4 different times, i.e. \(t_1 = 71\,\text {s}\), \(t_2 = 172\,\text {s}\) (maximum crystal size), \(t_3 = 262\,\text {s}\) and \(t_4 = 302\,\text {s}\). The non-faceted shape of the solid-liquid front can be explained by the non-dimensional Jackson factor,[24] a measure of the roughness of the interface

$$\begin{aligned} \alpha = \xi \frac{\Delta S_f}{R} \approx 1.88\;, \end{aligned}$$
(1)

where \(\xi\) depends on the crystallography and is taken to be 1, \(\Delta S_f\) is the entropy of fusion for pure wollastonite and R is the ideal gas constant. The entropy of fusion is taken from Reference 9 and is determined to be \(\Delta S_f = 15.63\, \text {J}\,\text {mol}^{-1} \text {K}^{-1}\) for pure wollastonite. A Jackson factor \(\alpha < 2\) indicates non-facted growth. A transition of faceted to non-faceted growth of wollastonite is reported by Heulens et al.[9] depending on the iso-thermal undercooling during crystallisation. A switch from faceted to non-faceted growth is not observed during the cyclic partial phase transformations in this work.

The maximum extension of the solid phase during one cycle is characterized by the area \(A_0\). The corresponding evolution of the normalized apparent area \(A/A_0\) with the according temperature profile is shown in Figure 7(b). The solid fraction starts to grow at a normalized area \(A/A_0\), which is 0 at time \(t = 0\), and reaches approximately \(0.33 A_0\) at \(t_1=71\,\text {s}\). The maximum extension of the solid fraction is reached at approximately \(172\,\text {s}\). After that, the solid phase starts to shrink down again with rising temperature reaching \(0.64 A_0\) at \(t_3=262\,\text {s}\) and 0.1\(A_0\) at \(t_4=302\,\text {s}\), respectively. The times corresponding to the snapshots shown in Figure 7(a) are also indicated in Figure 7(b) via the dashed blue lines.

Fig. 7
figure 7

Representative results from the image analysis for the incongruent case at times \(t_1\) = \(71\,\text {s}\), \(t_2\) = \(172\,\text {s}\), \(t_3\) = \(262\,\text {s}\) and \(t_4\) = \(302\,\text {s}\) (a). The observation frame is colored red, the solid and liquid phase regions within the observation window are indicated in blue and white, respectively. The corresponding normalized apparent area of the solid phase in the observation window vs time for one transformation cycle (b). The temperature during the transformation cycle is given via the orange line (Color figure online)

Full size image

Modelling of Cyclic Partial Phase Transformations

The kinetics of cyclic partial phase transformations are simulated in order to complement the experimental observations and interpret them. The growing and shrinking of the solid phase is simulated by means of a sharp (i.e. infinitely thin) interface model. The numerical model takes the diffusion of the components \(\text {CaO}\) and \(\text {SiO}_2\) in the liquid phase and the interface reaction at the solid/liquid interface into account. First, the thermodynamic conditions at the sharp interface are discussed. The simplest approach to the thermodynamics at the solid/liquid interface for diffusional phase transformations is the local equilibrium condition, where the chemical potentials \(\mu _{i}\) of the components i of an N-component system at the liquid and solid side of the interface are equal

$$\begin{aligned} \mu ^{\text {liquid}}_{i} = \mu ^{\text {solid}}_{i} \;,\;\;\;\;\; i = 1,...,N . \end{aligned}$$
(2)

A graphical representation of the local equilibrium at the interface is given via the well known common tangent construction in the binary molar Gibbs energy diagram (\(G_{\text {m}}\) is plotted vs the mole fraction x here \(x_{\text {CaO}}\)), see Figure 8(a). The molar Gibbs energy functions of the liquid and solid phases are represented in red and green, respectively. The solid phase (wollastonite) is modelled as a pure compound with a defined composition.

No chemical driving force is acting on the interface due to the local equilibrium assumed at the sharp interface. Zero driving force implies for a migrating sharp interface that the interfacial reaction is negligible and not rate-controlling. Local equilibrium at the interface is certainly a sufficient approximation for diffusive phase transformations at high (homologous) temperatures in many cases. The local equilibrium approach is frequently used for simulating phase transformations in metallurgy and materials science. In this context, the commercial tool DICTRA should be also mentioned. It is a software for calculating the kinetics of purely diffusion controlled phase transformations,[25,26]

However, diffusion processes in the liquid bulk do not play any role in case of congruent melting. In case of a positive driving force for phase transformation the sharp interface should migrate with infinite speed when there are no dissipative processes at the interface and in the bulk material. It is, however, evident from experience and from experiments shown later that the interface migrates with a certain finite velocity also in case of congruent phase transformations due to interfacial reactions. These interfacial reactions are considered in the model by a deviation from local equilibrium conditions at the sharp interface. Dissipation due to the interfacial reactions is considered by a finite mobility of the sharp interface.

The chemical driving force \(\Delta f^{\text {chem}}\) at the interface is expressed by the jump of the chemical potentials \(\mu _{\text {i}}\) at the interface and the mole fractions of the components at the parent side of the interface \(x^0_{\text {i}}\). For the binary case the chemical driving force is

$$\begin{aligned} \Delta f^{\text {chem}} = x^0 (\mu _1^{\text {liquid}} - \mu _1^{\text {solid}} ) + (1-x^0) (\mu _2^{\text {liquid}} - \mu _2^{\text {solid}} ) \;. \end{aligned}$$
(3)

Other contributions to the total driving force stemming e.g. from contributions of the surface energy in case of small particles or from mechanical stresses are neglected.

The contact conditions at a migrating sharp interface with a finite mobility can be derived by applying the thermodynamic extremal principle, see e.g. [27,28,29]. It follows from the thermodynamic extremal principle that the jumps \([[\mu _{\text {i}}]]\) of the chemical potentials of the (substitutional) components i at the interface must be equal (equal jump condition). Hence, for an N-component system the equal jump conditions at the interface yield:

$$\begin{aligned}{}[[\mu _1]] = [[\mu _2]] = ... = [[\mu _N]] \;. \end{aligned}$$
(4)

It follows from these equal jump conditions that \(\Delta f^{\text {chem}}\) simplifies to the equal jump in the chemical potential of component i, i.e. \(\Delta f^{\text {chem}}=[[\mu _i]]\). Thus, graphically, the equal jump conditions are represented by parallel tangents in case of a binary system. The vertical distance between the parallel tangents equals the chemical driving force \(\Delta f^{\text {chem}}\) acting on the interface as depicted in Figure 8(b).

Fig. 8
figure 8

Sketch of molar Gibbs energy vs mole fraction diagrams for two different thermodynamic scenarios at the solid/liquid interface in binary \(\text {CaO}\)–\(\text {SiO}_2\); (a) represents the local equilibrium condition (common tangent construction) and (b) the equal jump condition (parallel tangent construction) during melting. The solid phase (i.e. wollastonite) is modelled as a line compound with a defined composition

Full size image

From linear non-equilibrium thermodynamics the phenomenological equations for the diffusive fluxes \(j_i\) of the components i in z-direction follow

$$\begin{aligned} j_i = -\sum ^{N-1}_{k=1} L_{ik} \frac{\partial \mu _k}{\partial z} \; , \end{aligned}$$
(5)

where \(L_{ik}\) are the coefficients of the symmetric, positive definite Onsager matrix, and the index k denotes component k. Details can e.g. be found in References 30 and 31. The diffusive flux \(j_1\) of component 1 in a 1-2-binary system in z-direction is

$$\begin{aligned} j_1 = -L_{1 1}\frac{\partial \mu _1}{\partial z}-L_{1 2}\frac{\partial \mu _2}{\partial z} \; . \end{aligned}$$
(6)

Here, component 1 and component 2 represent \(\text {CaO}\) and \(\text {SiO}_2\), respectively. For a binary system there is only one independent composition variable x and only one driving force for diffusion. Thus, following Hillert[20], Eq. [6] can be reformulated as

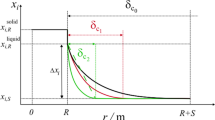
$$\begin{aligned} j_1 = -\left( L_{11} - L_{12} \frac{x}{1-x} \right) \frac{\partial \mu _1}{\partial x} \frac{\partial x}{\partial z} = -\frac{D_1}{V_{\text {M}}}\frac{\partial x}{\partial z}\;, \end{aligned}$$
(7)

where \(D_1\) denotes the intrinsic diffusion coefficient of component 1 and \(V_{\text {M}}\) denotes the molar volume. The intrinsic diffusion coefficient \(D_1\) and the molar volume \(V_{\text {M}}\) are assumed to be spatially constant in the model. The partial differential equations for solving the diffusion problems are integrated numerically by means of finite differences and are solved together with the mass balances at the interface. A geometric scheme of the sharp interface model is shown in Figure 9. The temperature dependence of the finite interface mobility M is assumed to follow the Arrhenius relation:

$$\begin{aligned} M = M_0 \exp \left( \frac{-Q_{\text {M}}}{RT}\right) \; , \end{aligned}$$
(8)

where \(M_0\) is a temperature-independent pre-exponential factor and \(Q_{\text {M}}\) denotes the activation energy for the movement of the interface. The gas constant is denoted by R and T is the absolute temperature.

In the sense of linear non-equilibrium thermodynamics the thermodynamic force, here the chemical driving force \(\Delta f^{\text {chem}}\), and the thermodynamic flow, the interface velocity v, are linearly related:

$$\begin{aligned} v = \frac{M}{V_{\text {M}}} \Delta f^{\text {chem}} \;. \end{aligned}$$
(9)

The Gibbs energy of the liquid phase and the chemical potentials of its constituents are calculated by means of the modified quasi-chemical model[32,33,34]. The thermodynamic parameters needed for calculating the Gibbs energies and chemical potentials of the relevant phases in the binary \(\text {CaO}\) - \(\text {SiO}_2\) system are taken from the assessment of Eriksson and Pelton[35]. The calculations are executed by means of a recently developed thermodynamic software package[36].

Fig. 9
figure 9

Geometric representation of the sharp interface model. The solid and liquid phase are separated by a sharp interface moving with a finite velocity v. Diffusion is only considered in the liquid phase. The space of the liquid phase is discretized by means of a finite difference scheme. The grid point distances are given by \(\Delta z_l\) with \(l=0\,...\,n-1\). The solid phase is assumed to have a fixed composition of \(x^{\text {solid}}_{\text {CaO}}\). The composition in the liquid adjacent to the interface is denoted \(x^{\text {liq,I}}_{\text {CaO}}\) and is calculated by means of the local equilibrium condition Eq. [2] or the equal jump condition Eq. [4] at the interface, respectively. The bulk composition of the liquid phase is \(x^{\text {liq,bulk}}_{\text {CaO}}\). A shrinking particle is depicted in this figure, however, the same model also allows for particle growth with the interface velocity in the opposite direction

Full size image

Results and Discussion

Figure 10 shows the evolution of the normalized apparent area \(A/A_0\) of the solid phase during a representative transformation cycle for a congruent and an incongruent phase transformation, respectively. Experimental results in the \(\text {CaO}\)-\(\text {SiO}_2\) system indicate that the features of congruent and incongruent phase transformations are diverging. A representative transformation cycle for the congruent phase transformation is shown in Figure 10 (The congruent case is indicated by a double line and a triangle symbol). First, the normalized area \(A/A_0\) of the solid grows during the cooling phase of the transformation cycle. This growing stage is indicated in blue in Figure 10. After reaching the minimum temperature, the sample is heated up immediately. Consequently, the temperature rises again while the area of the solid phase is still subject to growth. Following[15], this stage is called the inverse stage and is highlighted in red. Finally, the solid phase shrinks again with rising temperature (black line). Contrary to the congruent case, the incongruent phase transformation (The incongruent case is indicated by a single line and a circle symbol, Figure 10) is characterized by an additional pronounced stage where the slope of \(A/A_0(T)\) approaches almost zero. This stage is highlighted in green in Figure 10 and is referred to as stagnant stage, see also Chen et al.[15]. The effect of thermal expansion or contraction is too marginal to be clearly detected by means of the experimental technique applied in this work. Growth of the solid on behalf of the liquid phase or vice versa does not occur during the stagnant stage. The differences in the transformation kinetics become even clearer by focusing on the reversal stages of these phase transformations. Apparently, the normalized area profile for the congruent case is significantly sharper compared to the incongruent case. It is evident that the velocity of the interface in the congruent case changes rapidly after reaching its maximum extension. In contrast to congruent phase transformations, the normalized area during cycling of incongruent phase transformations remains almost constant during a certain period of time, i.e. stagnant stage occurs. This phenomenon will be investigated numerically in the following.

Fig. 10
figure 10

Evolution of normalized area of wollastonite during a representative transformation cycle subject to the congruent (double line and open triangle symbols) and incongruent (solid line and open circle symbols) regime. The circular arrow indicates time direction and \(\vartheta _{\text {ic}}\) and \(\vartheta _{\text {c}}\) the temperatures for the incongruent (ic) and congruent (c) case, respectively

Full size image

The calculated interface position of the solid phase is plotted vs time during a partial cyclic phase transformation in Figure 11(a). The dotted, color-coded vertical lines indicate four different times. The mole fraction profiles of CaO near the solid/liquid interface are displayed for these transformation times in Figure 11(b). It can be seen that in the time interval between \(t_2 = 140\,\text {s}\) and \(t_3 = 174\,\text {s}\) the interface behaves almost stagnant according to the numerical model. Accordingly, the mole fraction jump at the interface remains (almost) at the same position (see Figure 11(b)).This time interval is highlighted in green and corresponds to the stagnant stage also found experimentally (shown in Figure 10(b)). Due to the diffusion-controlled manner of the incongruent phase transformation the interface velocity can not change its direction immediately after reaching the peak position as long as the concentration field around the interface does not support the net material transport in the new direction. The numerical results are compared to HT-CSLM observations in Figure 12. The features of the area profile are captured by means of the sharp interface model. It is worth noting that the complex heat flow through the experimental set-up is not considered in the calculations in this work. Hence, the temperature is considered evenly-distributed over the sample in the numerical model and the temperature values for the calculations are taken directly from the measured time/temperature data pairs. Although the crystal growth takes place in three-dimensional space, the motion of the interface and the area of the wollastonite during partial cyclic phase transformations can be observed by HT-CSLM in two dimensions only. We assume that the experimentally observed mean value of the interface migration over the interface length can be approximated by the mean movement of a planar front, i.e. the originally 3D interface migration is reduced to 1D modelling problem.

Bulk diffusion is not required during congruent phase transformations. The interface velocity in the congruent case is solely determined by the temperature dependent mobility M(T) of the interface and the (also temperature dependent) driving force \(\Delta f^{\text {chem}}\) acting on the interface. The calculated area evolution \(A/A_0\) during one transformation cycle under the congruent regime is shown in Figure 13 and is compared to the experimental results stemming from HT-CSLM data. Compared to the incongruent case no pronounced stagnant stage can be identified. The velocity of the interface follows the direction dictated by the driving force acting on it. The model qualitatively agrees with the experimental observations. The peak of the normalized area profile of the simulated transformation cycle is located at a higher value in time compared to the experimental results. This might be due to a deviation of the temperature at the solid/liquid interface from the temperature measurement. The effective mobility of the solid/liquid interface is estimated by comparing the interface velocity evaluated from the data stemming from HT-CSLM experiments under the congruent regime with the numerical results. Using Eq. [9] the simulated velocities are fitted to the experimental values to obtain the effective mobility of the interface. The activation energy \(Q_{\text {M}}\) for the movement of the interface is estimated in a first attempt from the activation energy of self-diffusion of \(\text {Ca}^{45}\) in molten \(\text {CaO}\)–\(\text {SiO}_2\) slag with a composition of \(x_{\text {CaO}}=0.512\), as determined by Keller et al.[37]. Hence, \(Q_{\text {M}}\) is set to \(142\cdot 10^{3}\) \(\text {Jmol}^{-1}\). This value can also be found in the well-known Slag Atlas[38]. The molar volume \(V_{\text {M}}\) is assumed to be equal in both phases and is set to the value \(4\cdot 10^{-5}\) \(\text {m}^3\,\text {mol}^{-1}\). Hence, \(M_0\) remains as the primary fitting parameter and a value of \(5.5\cdot 10^{-9}\) \(\text {m}^2\,\text {s}\,\text {kg}^{-1}\) is obtained from the optimal fit.

Fig. 11
figure 11

Simulated evolution of the interface position during a transformation cycle (a) subject to the incongruent scheme; the orange line represents the temperature evolution during the transformation cycle. The green line highlights the predicted stagnant stage. The mole fraction profiles of CaO at four different times during the cycle are shown in (b) (Color figure online)

Full size image
Fig. 12
figure 12

Growth and shrinkage of the normalized area of wollastonite during a transformation cycle subject to the incongruent regime. The experimental data (black) is shown in comparsion with simulated results (blue). The orange line represents the evolution of the temperature during the transformation cycle (Color figure online)

Full size image
Fig. 13
figure 13

Evolution of normalized area of wollastonite during a transformation cycle subject to the congruent regime. The experimental data (black) is shown in comparsion with simulated results (blue). The orange line represents the evolution of the temperature during this cycle (Color figure online)

Full size image

Conclusions and Outlook

The kinetics of cyclic partial phase transformations of wollastonite is investigated by means of HT-CSLM experiments. Two carefully selected slag compositions are used to provoke two different cases of phase transformations, namely, incongruent and congruent melting/solidification. It is assumed that the rate controlling dissipative processes are diffusion in the liquid phase and the interfacial reaction. Based on these assumptions the kinetics of the cyclic partial phase transformation of wollastonite in liquid \(\text {CaO}\)–\(\text {SiO}_2\) is modelled by a sharp interface model. The experimental observations are interpreted by means of the numerical results. Thereby, the following conclusions can be drawn:

  • Similarly to investigations of austenite/ferrite cyclic partial phase transformations in previous works (see References 14,15,16), stagnant stages (i.e. periods with no or almost no interface migration) are observed during cyclic partial melting and solidification in the case of incongruent transformations.

  • In contrast to stagnant stages observed during incongruent phase transformations, sudden changes of the direction of the interface migration occur during congruent cyclic partial melting and solidification.

  • The rather simple model conceptions used in this work − namely bulk diffusion controlled phase transformation in the incongruent case and interface reaction controlled phase transformation in the congruent case − suffice to describe the experimentally observed features of these cyclic phase transformations.

  • A combination of in-situ HT-CSLM experiments and physically based modelling provides insight into microstructural changes during heat treatment.

  • Physically based modelling contributes to understand details in the dissipative processes occurring during congruent and incongruent melting and solidification. This knowledge may be applied to simulate the dissolution of oxide particles in slags or may support the design of new refractory or other ceramic-based materials.