Introduction

Magnetite ore is one of the important resources for ironmaking plants. The global magnetite ore production is approximately 583 million tons per year accounting for 28 pct of the total iron ore production.[1] In some countries, such as South Australia, the major iron ore deposit is magnetite.[2] The current commercial practice of magnetite ore fines usually requires pelletization to produce iron ore pellets with appropriate size and strength.[3] However, the pelletizing process requires additional energy and cost and generates CO2 emissions. One possible concept for future crude steel production is using a hydrogen-based fluidized bed to produce hydrogen direct reduced iron (HDRI), followed by an electric arc furnace (EAF) process.[4,5] Therefore, the production of HDRI using magnetite ore fines in a hydrogen-induced fluidized bed becomes of great interest. The hydrogen-based fine-ore reduction (HYFOR) process developed by Primetals Technologies is one of the successful examples. The HYFOR process allows for the operation of any type of iron ore fines with particle sizes of 100 pct < 150 μm.[6] In the case of using magnetite ore fines, prior oxidation occurs in the preheating stage. A series of laboratory-scale experiments showed that the prior oxidation of magnetite was helpful to improve its fluidization and reduction behavior.[7,8,9] Thus, it is of great importance to understand the oxidation mechanisms of magnetite ore fines for optimizing the process route.

The exothermic effect, structural evolution, and kinetic analysis regarding the oxidation of magnetite were summarized in our previous work.[10,11] In general, the oxidation of magnetite experienced two stages, where the magnetite was oxidized into an intermediate phase and further oxidized to α-Fe2O3. During the oxidation, whisker or rough pleated structures of hematite were formed on the surface of magnetite particles. The rate-limiting step for oxidation of magnetite in particle scale was generally solid-state diffusion which can be well described by parabolic law. The diffusion of oxygen into/within the magnetite particles was not the rate-limiting step. There are many kinetic studies on the oxidation of magnetite at the particle scale using thermogravimetric analysis (TGA).[12,13,14,15,16] In addition, some post-mortem X-ray diffraction (XRD) measurements were conducted to study crystal transformation after the oxidation of magnetite. It was found that magnetite from different mines showed different lattice constants due to various types of gangue elements.[17] .The lattice constant of oxidized magnetite also differed after oxidation at different temperatures.[18] The strain/stress occurring in the lattice should promote the nucleation of α-Fe2O3 and the crystallite size of magnetite governed the formation of γ-Fe2O3 and the oxidation kinetics.[19] The crystallite size of the oxidized magnetite calculated based on the Scherrer equation was comparable to that measured by transmission electron microscopy (TEM), which proved the accuracy of the XRD method for obtaining the crystallite size.[20] However, little information is available in the literature on the phase transition at the crystal scale during oxidizing magnetite, which limits the understanding of the oxidation mechanisms of magnetite. The objective of the present study is to investigate the thermal transformation of magnetite ore fines at the crystal scale via in situ high-temperature XRD (HT-XRD) during oxidation. The findings provide deeper insights into the phase transformation from magnetite to hematite under an oxidation condition.

Experimental Procedures

Materials

Two commercial magnetite ore brands were investigated in this study and their chemical compositions are listed in Table I. The particle size distributions and apparent densities of the ores were characterized by CILAS 1064 particle size analyzer and Ultrapycnometer 1000 density analyzer, respectively. The results are listed in Table II. The raw ores were dried at 110 °C for 6 h before all the following tests.

Table I Chemical Analysis of the Raw Magnetite Samples, (Wt Pct)[11]
Full size table
Table II Particle Size Distributions and Density of the Raw Magnetite Samples[11]
Full size table

In Situ High-Temperature X-Ray Diffraction (HT-XRD)

The HT-XRD analyses were performed on a Rigaku Ultima IV XRD diffractometer with a Cu target. The Kα radiation was filtered as the X-ray source. The measurement step size was 0.02 deg and the sampling time was 0.15 s/step. In each measurement, 300 mg of material was placed on a platinum heating strip and heated in the HTK-16 high-temperature chamber (Anton Paar) to 1000 °C at a heating rate of 100 °C/min. The material was placed in a very thin layer to avoid thermal gradients along the height. It is difficult to determine the thickness of the layer. The layer was composed of a stack of approximately 3 magnetite particles and supposed to be thinner than 150 μm. The in situ HT-XRD measurements were conducted at temperatures of 400 °C, 600 °C, 800 °C, and 1000 °C, as shown in Figure 1. The air could be exchanged between the facility chamber and the outside. Due to the small amount of magnetite, the change of oxygen partial pressure was negligible. The oxygen partial pressure was assumed to be the same as the ambient atmosphere. Before and after the oxidation experiments, the XRD measurements were conducted at room temperature with a scanning angle between 25 and 65 deg. It should be noted that the temperature ramping was halted and the material was kept at a fixed temperature during the in situ HT-XRD measurements. The oxidation reaction continued during the HT-XRD scans. To minimize the duration of the HT-XRD measurements and increase the time resolution, the scanning angle was set in a narrow range between 32 and 41 deg, where three hematite peaks and two magnetite peaks could be observed. In this case, each HT-XRD measurement took around 67.5 s.

Fig. 1
figure 1

Temperature profile for HT-XRD measurements

Full size image

HT-XRD Data Treatment

The Rietveld refinement method was widely used for phase quantification in ironmaking area.[21,22,23,24] At current study, the Jade 6.0 software provided by Materials data Inc. was employed to identify and fit the diffraction peaks in this study. The overlapped peaks of magnetite and hematite at around 35 deg were successfully separated by refinement in Jade 6.0 software, and the location and profile of individual peaks were obtained, as shown in Figure 2. Besides, the quantitative information of crystal information, such as lattice constants,[25] crystallite size,[26] and phase fraction,[27] can be obtained.

Fig. 2
figure 2

Rietveld refinement peak profile of Ore A at different temperatures: (a) 600 °C and (b) 800 °C

Full size image

Determination of Lattice Constants

Based on our previous TGA tests, the oxidation started at around 200 °C then reached the first peak at around 330 °C and the second peak started at around 400 °C.[11] The oxidation product was supposed to be γ-Fe2O3 between 200 °C and 400 °C. Above 400 °C, γ-Fe2O3 transformed into α-Fe2O3. In the present study, the oxidation temperature was higher than 400 °C, and thus only α-Fe2O3 was expected to be the oxidation product (hereafter, α-Fe2O3 is referred to as Fe2O3). Therefore, two crystal structures were considered: Fe3O4 (cubic close-packed crystal) and Fe2O3 (hexagonal close-packed crystal). The relationship between interplanar spacings (d), lattice constants (a), and crystal planes {hkl} are expressed in Eqs. [1] and [2].[28] When a specific plane and corresponding interplanar spacing are known, the lattice constants can be calculated. The interplanar spacing can be obtained by Bragg's law as shown in Eq. [3].

$$ {\text{Cubic}}\;{\text{close-packed}}\;{\text{crystal}}: \frac{1}{{d^{2} }} = \frac{{h^{2} + k^{2} + l^{2} }}{{a^{2} }} $$
(1)
$$ {\text{Hexagonal}}\;{\text{close-packed}}\;{\text{crystal}}: \;\frac{1}{{d^{2} }} = \frac{4}{3}\frac{{\left( {h^{2} + k^{2} + hk} \right)}}{{a^{2} }} + \frac{{l^{2} }}{{c^{2} }} $$
(2)
$$ {\text{Bragg}}^{\prime}s\;{\text{law}}:d\; = \;\frac{n\lambda }{{2{\text{Sin}} \theta }}, $$
(3)

where \(d\) is the interplanar spacing; \(a\) and \(c\) are the lattice constants, {\(hkl\)} is the crystal plane; n is the diffraction order, and here the value is 1.

Determination of Crystallite Size

Crystallite size (\(D\)) can be calculated using the Scherrer equation, as given in Eq. [4]. It should be noted that the crystallite size refers to the average thickness perpendicular to the (hkl) planes. The (110) and (104) planes of Fe2O3 crystal were chosen for quantifying the crystallite size. Because these two peaks exhibit relatively high intensities and have similar instrumental broadening conditions (similar peak position).[29] As shown in Figure 3, the (110) plane is parallel to the c axis and (104) plane is at a small angle to the a/b axis.[29] Therefore, the crystallite size along the c axis and a/b axis can be calculated according to Eqs. [5], [6].

$$ D = \frac{K\lambda }{{\beta cos\theta }} $$
(4)
$$ D_{a/b} = D_{110} \times {\text{cos}}\alpha_{110} $$
(5)
$$ D_{c} = D_{104} \times {\text{cos}}\alpha_{104}, $$
(6)

where D is crystallite size, nm; K is 0.94 (Scherrer constant); λ is 0.15406 nm (the wavelength of Kα Cu X-ray source); β is full width at half maximum (FWHM), radians; θ is peak position, radians; \(D_{a/b}\) and \(D_{c}\) represent the crystallite size calculated based on (110) and (104) peaks; \(\alpha_{110}\) is the angle between [110] direction and x–y plane; \(\alpha_{104}\) is the angle between the [104] direction and the y–z plane. Here, \({\text{cos}}\alpha_{110}\) = 1 and \({\text{cos}}\alpha_{104}\) = 0.6192.[29]

Fig. 3
figure 3

Schematic of Fe2O3 crystal: (a) (110) plane and (b) (104) plane

Full size image

Determination of Oxidation Degree

The matrix-flushing method[30,31] was used to obtain the content of Fe3O4 and Fe2O3. The relative mass content of each phase is proportional to the ratio between its peak intensity and relative intensity ratio (RIR). The RIR value of each phase can be found in the PDF card database. The RIRs of the Fe3O4 and Fe2O3 phases are 4.9 and 3.2, respectively. The impurities were not considered in the calculation. The content of Fe2O3 and Fe3O4 can be calculated based on Eqs. [7], [8].[11]

$$ x_{H} /x_{M} = \frac{{I_{H} }}{{k_{H} }}/\frac{{I_{M} }}{{k_{M} }} $$
(7)
$$ x_{H} + x_{M} = 1, $$
(8)

where \(x_{H}\) and \(x_{M}\) are the relative mass content of Fe2O3 and Fe3O4. \(I_{H}\), \(I_{M}\), \(k_{H}\) , and \(k_{M}\) are the intensities and RIR values of Fe2O3 and Fe3O4, respectively.

Kapelyushin et al.[32] calculated the reduction degree of Fe3O4 in the CO-CO2 atmosphere based on HT-XRD analysis. The oxidation degree of Fe3O4 can be obtained by a similar method. The initial mass content of Fe3O4 was calculated via the mass balance of iron. Hence, the theoretical weight gain can be obtained as given in Eqs. [9], [10]. The actual weight gain was calculated based on the Fe2O3 mass content via Eq. [11]. Thereafter, the oxidation degree (w) can be obtained by Eq. [12].[33,34]

$$ m_{M} = x_{M} + \frac{{x_{H} }}{{W_{H} }} \times \frac{2}{3} \times W_{M} $$
(9)
$$ \Delta m_{{ {\text{theory}}}} \; = \;\frac{{m_{M} }}{{W_{M} }} \times \frac{{W_{O} }}{4} $$
(10)
$$ \Delta m = \frac{{x_{H} }}{{W_{H} }} \times \frac{2}{3} \times \frac{{W_{O} }}{4} $$
(11)
$$ w = \frac{\Delta m}{{\Delta m_{ theory} }}\; \times \;100\;{\text{pct}}, $$
(12)

where \(W_{H} ,\) \(W_{M}\), and \(W_{O}\) are mole masses of Fe2O3, Fe3O4, and O2, respectively. \(m_{M}\), \(\Delta m_{ theory}\), \(\Delta m\), and w are the initial mass content of Fe3O4, theoretical weight gain, actual weight gain, and oxidation degree.

Results and Discussion

Oxidation of Magnetite

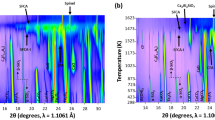
Figure 4 shows the oxidation behavior of two ores at different temperatures probed by HT-XRD. Two ores revealed similar oxidation behavior, as suggested by the diffraction patterns. All the peaks shifted to a lower diffraction angle with an increase in temperature due to thermal expansion.[35,36,37] The (104) peak of Fe2O3 firstly appeared at 400 °C, as shown in Figures 4(a) and (c). With an increase in temperature, the intensity of the (104) peak increased, indicating a higher fraction of Fe2O3. The (311) peak of Fe3O4 vanished at 1000 °C, representing deep oxidation of Fe3O4. The width of (104) peak became narrower with increasing temperature, which suggested the growth of Fe2O3 crystallite.

Fig. 4
figure 4

in situ HT-XRD patterns at different temperatures: (a), (b) Ore A; (c), (d) Ore B

Full size image

Oxidation Degree

The oxidation degrees of both ores at different temperatures are shown in Figure 5. Ore A was easier to be oxidized than Ore B, as indicated by its faster kinetics. The oxidation degree was lower than 10 pct at 400 °C in both cases. When the temperature increased to 600 °C, the oxidation degree increased significantly. Above 800 °C, the oxidation rate slowed down. The sigmoid-shaped oxidation degree curve indicated that the kinetics followed the parabolic law, where the solid diffusion of ions was the rate-limiting step. The oxidation mechanism was explained in our previous study.[11] Each magnetite crystal unit contains eight Fe3O4 molecules, i.e., 32 oxygen anions and 24 iron cations (16 Fe3+ and 8 Fe2+). The oxygen anions present a cubic close-packed structure, where 96 interstices exist. Only 8 out of 64 tetrahedral interstices are occupied by Fe3+ cations. 16 out of 32 octahedral interstices are occupied by 8 Fe3+ cations and 8 Fe2+ cations.[11] Due to so many interstices, the iron cations can move easily within the crystal lattice. The O2− anion can hardly move due to its bigger size. From the crystal scale, when an oxygen atom is trapped by Fe3O4 for phase transformation, two electrons are taken from the crystal by the oxygen atom. In the meanwhile, two positively charged holes 2 h + are generated in the place of the previous electrons for a neutral local charge in the crystal. Then Fe2+ cation may capture the charged hole h+ and becomes Fe3+ cation. In later oxidation stage, due to the high amount of Fe3+ cations, the charged hole h+ has less opportunity to meet Fe2+ cations. In the contrast, the charged hole h+ decreases the mobility of the iron cations and expand the crystal unit.

Fig. 5
figure 5

The oxidation degrees of Ore A and B at different temperatures: (a) Ore A; (b) Ore B

Full size image

Evolution of Lattice Constants

Table III summarizes the lattice constants of Fe3O4 in the ores at different temperatures. The results are comparable to those in the literature. The change in lattice constant with increasing temperature is supposed to be caused by thermal expansion and lattice modification during oxidation.[18] As shown in Table III, the lattice constant at a specific temperature measured in this study was slightly larger than that in the literature. Such a difference might be due to a much higher oxygen partial pressure in the present study, as the magnetite was oxidized under an air atmosphere. This condition could result in a larger lattice constant of magnetite due to partial oxidation[38] (i.e., a higher oxygen occupancy in the lattice). The temperature dependence of the lattice constant can be represented by polynomials up to the fifth order.[39] Here, the relation between lattice constant and temperature was successfully fitted with the second-order polynomials (Figure 6), within a temperature range of 25 °C to 800 °C. The temperature-dependent lattice constant of Fe3O4 can be described as follows: \(a = 2.53 \times 10^{ - 8} \times {\text{T}}^{2} + 8.64 \times 10^{ - 5} \times {\text{T}} + 8.4132\). At the higher temperature (e.g., 1000 °C), the (222) peak of Fe3O4 disappeared, which reduced the accuracy in the assessment of the lattice constant. Thus, the lattice constant at 1000 °C was not considered.

Table III The Lattice Constant and Volume of the Fe3O4 Cell Measured by High-Temperature X-Ray Diffraction During the Oxidation of Fe3O4 in Air
Full size table
Fig. 6
figure 6

The lattice constant of Fe3O4 as a function of temperature measured by high-temperature X-ray diffraction during oxidation of Fe3O4 in air

Full size image

Table IV lists the lattice constants of Fe2O3 at different temperatures. Based on Eq. [2], at least two peaks of Fe2O3 are required to obtain the lattice constant a and c for a trigonal crystal structure. Therefore, only one set of a and c can be calculated at each temperature in the current study. The lattice parameters of Fe2O3 measured in this study were slightly larger than those in the literature, where a was 5.01 to 5.04 Å and c was 13.68 to 13.73 Å in the temperature range of 300 °C to 800 °C.[41] Stefano et al.[37] studied the phase transformation from goethite (α-FeOOH) to hematite (α-Fe2O3) in the temperature range of 200 °C to 1000 °C by synchrotron powder diffraction. Hematite was formed by the release of the OH− groups of goethite phase. The hexagonally close-packed arrays of oxygen anions present in the parent goethite still remained in the newly formed hematite. Tatsuo et al.[42] studied the thermal expansion of hematite at high temperatures, where no chemical reaction occurred. In current study, the hematite was formed by the oxidation of magnetite. The oxygen anions are transferred from cubic close-packed arrays to the hexagonally close-packed arrays. The aforementioned three hematite phases were generated through distinct pathways. Figure 7 shows the relative increase in a and c of the three hematite phases. The correlation between lattice constants and temperature can be also fitted with second-order polynomials (Figure 8). The temperature-dependent lattice constant of Fe2O3 can be described as follows: \(a = - 2.81 \times 10^{ - 8} \times {\text{T}}^{2} + 8.76 \times 10^{ - 5} \times {\text{T}} + 5.0368; c = 3.01 \times 10^{ - 8} \times {\text{T}}^{2} + 1.09 \times 10^{ - 4} \times {\text{T}} + 13.7621\).

Table IV The Lattice Constant and Volume of the Fe2O3 Cell
Full size table
Fig. 7
figure 7

The relative increase in lattice parameters a and c of Fe2O3 at different temperatures[37,42]

Full size image
Fig. 8
figure 8

The lattice constants of Fe2O3 as a function of temperature: (a) lattice constant a; (b) lattice constant c

Full size image

The SiO2 was the dominant impurity in both ores. At current study, the maximum temperature was 1000 °C, the SiO2 was considered as inert phase. The size of Mg2+ (72 pm) is similar to Fe2+ (74 pm). Therefore, the influence of SiO2 and MgO on the lattice constant was ignored. The ore B contains more gangue minerals than the ore A. The impurities such as Al2O3 and CaO should have influence on the crystal cell of Fe3O4 and Fe2O3. Due to the smaller size of Al3+ (54 pm) than Fe3+ (65 pm), the substitution of Fe3+ by Al3+ in Fe3O4 or Fe2O3 crystal cell would result in a contraction of the cell volume. The Ca2+ cations either displace Fe2+ or occupy vacancies in Fe3O4 cell, both of which may result in an expansion of the crystal cell duo to the larger size of Ca2+ (100 pm). In other words, the Al3+ and Ca2+ show the opposite effect on the crystal size of Fe3O4 cell. Figure 9(a) illustrates the expansion of Fe3O4 crystal cell at different temperatures. The difference between the Ore A and Ore B was not significant. The Fe3O4 crystal cell expansion rate of Ore B was slightly smaller than that of Ore A, which can be explained by the substitution of Fe3+ by Al3+. However, the expansion rate at 800 °C was an exception. The Al3+ cations had better mobility within the Fe3O4 crystal cell than that of Ca2+ cations. Only at high temperature, i.e., 800 °C, the effect of Ca2+ cations became more dominant than Al3+ cations and promoted the expansion of the Fe3O4 crystal cell. Figure 9(b) shows the expansion of Fe2O3 crystal cell at different temperatures. The Fe2O3 crystal cell expansion rate of Ore B was slightly larger than that of Ore A at 600 °C and became more obvious at 800 °C. While at 1000 °C, the expansion rate of Ore B was smaller than that of Ore A. This phenomenon could be also explained by the combined effect of Al3+ and Ca2+ cations in the Ore B. Based on the stability diagram of Fe3O4-FeAl2O4 and Fe2O3-FeAlO3, Al3+ cations prefer to combine with Fe3O4 to form magnetite-based solid solution.[43] At 1000 °C, the oxidation degree of Ore B was 88.8 pct. With the decrease of magnetite phase, the Al3+ cations diffused from magnetite to hematite phase, resulting in the lower expansion rate of Ore B.

Fig. 9
figure 9

The expansion of crystal cell volume as a function of temperature: (a) Fe3O4; (b) Fe2O3

Full size image

Evolution of Crystallite Size of Fe2O3

Figure 10 shows the Fe2O3 crystallite sizes of Ore A and B along the c axis and the a/b axis. With an increase in temperature, more and more Fe3O4 was oxidized into Fe2O3, and thus the Fe2O3 crystallite in both ores grew, as shown in Figure 10. It was also observed in both ores that Fe2O3 grew faster along a/b axis (\(D_{a/b}\) in Figure 10) than c axis (\(D_{c} \) in Figure 10) in the crystal unit, especially in the beginning of oxidation. Also, the crystallite size along the a/b axis revealed a larger size than that along the c axis. Such findings suggested a growth habit of Fe2O3 during oxidation. It is worth noting that \(D_{a/b}\) and \(D_{c}\) were calculated based on the (110) and (104) peaks, respectively. In our previous study,[11] it was found that the surface energy of the (110) crystal surface was larger than that of the (104) crystal surface. The growth rates of the crystal faces are proportional to their surface energies, indicating a larger crystallite size along the a/b axis, which concurs well with the current study. The growth habit of Fe2O3 was also observed in TEM micrographs of Fe2O3 during the decomposition of goethite, where the Fe2O3 phase showed acicular morphology.[44] In general, it is believed that the Fe2O3 phase presents acicular microcrystals due to its crystallographic-dependent properties. Besides, the crystallite sizes of Ore A were slightly larger than that of Ore B at specific temperatures. It cannot be explained with present experimental data. It may be because of the higher contents of Al2O3 and MgO in Ore B, which inhibit the diffusion of Fe cations.[45,46] On the other hand, the crystallite sizes, calculated based on the peak (311), of the parent Fe3O4 phase of the Ore A and Ore B are 1027.7 Å and 812.6 Å, respectively. The larger crystallite size of Fe2O3 might inherit from the larger parent Fe3O4 phase.

Fig. 10
figure 10

The crystallite sizes of Ore A and B along the a/b axis and the c axis of a crystal cell at different temperatures: (a) Ore A; (b) Ore B

Full size image

Conclusions

In this study, the thermal transformation of two magnetite ore fines was investigated using in situ high-temperature X-ray diffraction (HT-XRD) during oxidation. The following conclusions can be obtained:

  1. (1)

    The crystal information, such as lattice constant and crystallite size, can be successfully characterized by HT-XRD. The peaks in HT-XRD patterns shifted to a lower diffraction angle with an increase in temperature due to thermal expansion. The intensity of the (104) peak of Fe2O3 increased with the increasing temperature, indicating an increase in the fraction of Fe2O3. The width of the (104) peak became narrower with the increasing temperature, suggesting a growing crystallite size of Fe2O3 during oxidation.

  2. (2)

    The lattice constants of Fe3O4 and Fe2O3 both increased with the temperature and followed second-order polynomials. The correlation of lattice constant and temperature can be expressed as follows:

    $$ {\text{Fe}}_{{3}} {\text{O}}_{{4}} :a = 2.53 \times 10^{ - 8} \times {\text{T}}^{2} + 8.64 \times 10^{ - 5} \times {\text{T}} + 8.4132; $$
    $$ {\text{Fe}}_{{2}} {\text{O}}_{{3}} :a = - 2.81 \times 10^{ - 8} \times {\text{T}}^{2} + 8.76 \times 10^{ - 5} \times {\text{T}} + 5.0368; c = 3.01 \times 10^{ - 8} \times {\text{T}}^{2} + 1.09 \times 10^{ - 4} \times {\text{T}} + 13.7621. $$
  3. (3)

    During oxidation, Fe3O4 transformed into Fe2O3. The growth of Fe2O3 revealed a certain growth habit. The growth rates of Fe2O3 crystallite along the a/b axis was faster than that in the c axis, thus showing acicular microcrystals. Such a morphology may affect the subsequent reduction, which requires further investigations.