Experimental Evaluation of MHD Modeling of EMS During Continuous Casting

Abstract

Electromagnetic stirring (EMS) has been recognized as a mature technique in steel industry to control the as-cast structure of steel continuous casting (CC), and computational magnetohydrodynamic (MHD) methods have been applied to study the EMS efficiency. Most MHD methods de-coupled the calculations of electromagnetic and flow fields or simplifications were made for the flow–electromagnetic interactions. However, the experimental validations of the MHD modeling have been rarely reported or very limited. In this study, we present a benchmark, i.e., a series of laboratory experiments, to evaluate the MHD methods, which have been typically applied for steel CC process. Specifically, a rotating magnetic field (RMF) with variable intensity and frequency is considered. First experiment is performed to measure the distribution of magnetic field without any loaded sample (casting); the second experiment is conducted to measure the RMF-induced torque on a cylindrical sample (different metals/alloys in solid state); the third experiment is (based on a special device) to measure the RMF-induced rotational velocity of the liquid metal (Ga75In25), which is enclosed in a cylindrical crucible. The MHD calculation is performed by coupling ANSYS Maxwell and ANSYS Fluent. The Lorentz force, as calculated by analytical equations, ANSYS Fluent addon MHD module, and external electromagnetic solver, is added as the source term in Navier–Stokes equation. By comparing the simulation results with the benchmark experiments, the calculation accuracy with different coupling methods and modification strategies is evaluated. Based on this, a necessary simplification strategy of the MHD method for CC is established, and application of the simplified MHD method to a CC process is demonstrated.

Introduction

Electromagnetic stirring (EMS) has been recognized as a mature technique and mandatorily implemented in the steel continuous casting (CC) process to control the melt flow and casting quality.^[1,2,3] It can extend the center equiaxed zone,^[4,5] refine the grain size,^[6] minimize the shrinkage porosity and macrosegregation,^[1,7,8] and even improve the surface quality and lower the risk of entrapment of non-metallic inclusions in the CC product.^[1,3] Both the rotating magnetic field (RMF) and traveling magnetic field (TMF) can be implemented. Based on the installed position in the CC, the EMS can be classified as mold electromagnetic stirring (M-EMS), secondary electromagnetic stirring (S-EMS), and final electromagnetic stirring (F-EMS).

To understand the principle of the EMS, in addition to the plant trials on real steel CC,^[9,10] laboratory experiments were performed based on model alloys of low melting point.^{[11,12,13,14,15]} When an RMF is applied on the melt sample, which is enclosed in a cylindrical crucible, the induced angular flow can drive a secondary poloidal flow.^[14] Although the secondary poloidal flow is approximately an order of magnitude slower than the angular flow, it transports the angular momentum out of the stirred region. It is known that it is not possible to obtain the flow information inside the casting via plant trials. The laboratory experiments are also limited to the model alloys of low melting point. Hence, the multiphase nature of solidification process has to be neglected. Therefore, computational magnetohydrodynamic (MHD) methods were popularly applied to examine the EMS efficiency.^[16,17] Many simulation studies have been conducted to calculate the EMS-driven flow and study its interaction with the solidification.^{[18,19,20,21]}

It is challenging to numerically couple the flow and electromagnetic (EM) fields in the industry process of CC. When the melt flow is subjected to a static magnetic field, similar to the electromagnetic brakes (EMBr),^[22,23] it is possible to couple the electromagnetic–flow interaction by programming it in the CFD solver. However, this coupling technique can hardly be applied for EMS where the implemented EM field is moving/changing. The ANSYS Fluent addon MHD module provides one coupled method for MHD calculations, but the external magnetic field (${\mathop{B}\limits^{\rightharpoonup}}_{0}$) should be known in advance. Specifically, the ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ field is imported into ANSYS Fluent, where the induced magnetic field ($\mathop{b}\limits^{\rightharpoonup}$), eddy current ($\mathop{J}\limits^{\rightharpoonup}$), and Lorentz forces (${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$) are calculated by solving User-Defined Scalar equations.^[24,25] The drawbacks of this method are as follows: (1) the addon MHD module is incompatible with the Eulerian–Eulerian multiphase approach on which most advanced solidification models were developed; (2) the calculation time-step ($\Delta t$) should be set extremely low to resolve the rotation of the imported ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ field. Therefore, the most widely used method is still based on the de-coupled method. Generally, there are two de-coupled methods to calculate the EM field. The first method is to use an analytical solution of the time-averaged ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$, which is derived based on an infinite solid conductive cylinder by assuming that the skin depth is significantly higher than the sample radius.^{[19,26,27,28]} Then, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is used to calculate the flow. This simplification is not in line with the case of high frequency, i.e., high magnetic Reynolds number (R_m), because the skin effect cannot be ignored.^[29,30] The second method is to calculate the EM field with a commercial EM solver, and then transfer ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ as a field function into the computational fluid dynamic (CFD) calculation.^[31] In this case, the EM field was solved mostly based on an assumption that the liquid melt is stationary.^[32,33,34] In addition to the de-coupled MHD calculations, further simplifications were often performed for CC. The ignorance of the existence of solid shell,^[33,35,36] where the maximal ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ applies, can overestimate the melt flow. Furthermore, Sun and Zhang^[32] used this de-coupled method to study the solidification of a bloom CC. However, the effect of the solidified shell on ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was ignored by using the same electrical conductivity for the liquid and solid steel. The main drawback of the de-coupled MHD method is that the influence of the melt flow on the EM field is ignored. Most recent studies appeared to ignore this effect.^{[18,32,33,34,37]} It is known that ignoring the flow effect on the EM field is only valid when the rotating angular speed ($\omega_{\ell }$) of the flow is not comparable to the applied EM angular speed ($\omega_{{\text{B}}}$). As reported in the previous studies,^[27,28,29] the effective ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ decreases with the induced $\omega_{\ell }$. Hence, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ should be modified by multiplying $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$. Nevertheless, most recent studies appear to ignore this effect.^{[18,32,33,34,37]} Therefore, the aforementioned de-coupled methods along with other assumptions should be carefully validated.

The aim of this study is to present a benchmark, i.e., a series of laboratory experiments, to validate the MHD methods that are typically employed for the steel CC process. An RMF field with variable intensity and frequency is considered. The MHD calculation is performed by coupling ANSYS Maxwell and ANSYS Fluent. An iteration scheme is proposed to consider the flow–electromagnetic interactions. Furthermore, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$, which is calculated with different methods and modification strategies, is termed as a source field in CFD calculations using coupled or de-coupled scheme. The calculation accuracy of different methods and modification strategies are compared. Based on this, the suitability of the MHD method with a necessary simplification strategy for CC is evaluated and discussed. Finally, application of the proposed MHD method to an industry process of CC is demonstrated.

Benchmark Experiments

The experiments were conducted on an upward Bridgman furnace equipped with an RMF. The RMF was generated by a two-pole inductor charged by a three-phase alternating current (AC). As shown in Figure 1(a), the diameter of the iron core of the inductor is 230 mm, and its height is equal to 300 mm. In the center of the inductor, the Bridgman-type furnace was assembled concentrically with the inductor, and the length of the measurement sample was 150 mm. Detailed information on the furnace is available in Reference 38. The application ranges of the facility are as follows: frequency f (30 to 400 Hz), magnetic induction $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ (0 to 150 mT), a withdrawal speed of sample in the Bridgman furnace v (0 to 0.8 mm/s), and temperature gradient G (0 to 10 K/mm).

Fig. 1

Schematic of experiment design. (a) Layout of the inductor and sample position; (b) sketch of torque measurement; (c) sketch of liquid velocity measurement

Experiment 1: Magnetic Field ($\mathop{B}\limits^{\rightharpoonup}$) Measurement

Without loading any sample, the $\mathop{B}\limits^{\rightharpoonup}$ field along the axis and in the azimuthal directions was measured with GM08 Gaussmeter (Hirts Magnetics).

Experiment 2: Torque ($\tau$) Measurement

As schematically shown in Figure 1(b), the sample is suspended in the inductor and fixed by an insulated organic sample holder (PA6 poliamid). The sample holder is connected to a cylindrical steel bar through a bearing housing. With the RMF load, the induced Lorentz force on the sample is transported to a digital dynamometer via the sample holder. All these components are placed coaxially in the height direction. To eliminate the error due to friction of the facility, the measured force that can initiate the movement of the sample was 0.34 N, i.e., Friction = 0.34 N. The Force exerted on the sample under different values of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ were measured. Hence, the Pull is calculated as Pull = Friction + Force. The torque $\tau = Pull*R$, where R denotes the radius of the sample. During the experiment, the sample is cooled by circulating water to maintain the sample at room temperature (20 °C). As listed in Table I, three metal samples with H = 150 mm and R = 10 mm were measured.

Table I Different Cylindrical Solid Samples Used for Torque Measurement

Experiment 3: Flow Velocity Measurement

A so-called pressure compensation method is applied to measure the RMF-induced rotating angular speed.^[39] This experiment was performed at room temperature with cold alloy Ga75In25. As shown in Figure 1(c), the closed cylindrical tank (Teflon) with two opening vessels (inner diameter = 1.0 mm) is filled with Ga75In25 alloy. The inner diameter of the tank was changeable (Table II), and its height was 100 mm. One vessel was at the center of the top surface, and another vessel was placed 0.2 mm to the inner surface of the tank. The maximal pressure was measured at position r = R-0.2 mm, so one vessel was set here to minimize the relative error of the measurements. The zero level before RMF load is denoted by the blue dash line in Figure 1(c). With the RMF load, a level difference (ΔH) develops between two vessels, as schematically indicated by the red dash lines in Figure 1(c). A compensatory pressure of air (P_comp) was applied on the peripheral vessel to set the melt back to zero level. In this manner, the pressure difference can be measured and used to calculate the liquid velocity. In this experiment, the penetration distance $\delta$ (Table II) is significantly higher than the sample radius, and the aspect ratio H/R ≥ 8. Therefore, the skin effect and end effect should be neglectable. As listed in Table II, the rotating velocities for eight cases with varying $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ are measured.

Table II Cases Performed for Flow Measurement Based on Ga75In25 Alloy

MHD Modeling and Simplification

Calculation Method 1: Analytical Solution

Instead of directly solving Maxwell’s equations, the analytical equations,^[27,29,40] as shown in Figure 2(a), are employed to calculated ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ (composed of ${\mathop{F}\limits^{\rightharpoonup}}_{{\theta }}$ and ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{r}}}$). Specifically, ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ should be known in advance. Typically, it is measured, and its distribution f(z) can be obtained by fitting the measurements. In this benchmark study, the inductor is significantly longer than the sample (Figure 1(a)). Hence, f(z) is assumed to be equal to 1. According to References 29 and 40, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{r}}}$ has a minor effect on the fluid flow when compared to ${\mathop{F}\limits^{\rightharpoonup}}_{{\theta }}$. Thus, we neglect it in this MHD simulation. As presented in Figure 2(a), the relative motion between the liquid and $\mathop{B}\limits^{\rightharpoonup}$ has been considered by a factor of $(1 - \omega_{\ell } /\omega_{{\text{B}}} )$.

Fig. 2

Sketch of different MHD calculation methods and coupling schemes: (a) Analytical solution; (b) Coupled simulation via ANSYS Fluent addon MHD module; and (c) Iteration scheme between EM and CFD solvers

Calculation Method 2: Coupled Simulation via ANSYS Fluent Addon MHD Module

${\mathop{B}\limits^{\rightharpoonup}}_{0}$ was first calculated via ANSYS Maxwell, and then it was imported into ANSYS Fluent. It should be noted that ANSYS Maxwell is another software package, which is de-coupled from ANSYS Fluent. In a time-dependent transient simulation, the rotation of ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ can be resolved with the given frequency f. As shown in Figure 2(b), given that ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ is known, only $\mathop{b}\limits^{\rightharpoonup}$ should be solved. Specifically, $\mathop{B}\limits^{\rightharpoonup}$ is a sum of ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ and $\mathop{b}\limits^{\rightharpoonup}$, i.e., $\mathop{B}\limits^{\rightharpoonup} = {\mathop{B}\limits^{\rightharpoonup}}_{0} + \mathop{b}\limits^{\rightharpoonup}$. The generated ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ due to the interaction between $\mathop{B}\limits^{\rightharpoonup}$ and $\mathop{J}\limits^{\rightharpoonup}$ can drive the liquid to flow. In turn, $\mathop{b}\limits^{\rightharpoonup}$ can be updated by the forced flow ($\mathop{u}\limits^{\rightharpoonup}$) to further modify $\mathop{B}\limits^{\rightharpoonup}$, $\mathop{J}\limits^{\rightharpoonup}$, and ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$. When the conductive liquid is heated due to the generated $Q_{{\text{J}}}$, the electrical conductivity can be updated according to local temperature, which in turn affects $\mathop{b}\limits^{\rightharpoonup}$ and $\mathop{u}\limits^{\rightharpoonup}$. The coupling between $\mathop{B}\limits^{\rightharpoonup}$, $\mathop{u}\limits^{\rightharpoonup}$, and T is automatically solved in ANSYS Fluent.

Calculation Method 3: Iteration Scheme Between EM and CFD Solvers

The MHD calculation is performed by combining ANSYS Maxwell and ANSYS Fluent. An iteration scheme, as shown in Figure 2(c), is proposed to consider the flow–electromagnetic interaction. Specifically, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was calculated via the EM solver, which was used to solve Maxwell equations. The extracted ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was transported to the CFD solver. According to Roplekar and Dantzig,^[28] ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was modified by multiplying $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$ before applying it as a source term for the Navier–Stokes equation. Then, the calculated averaged liquid rotating angular velocity, $\overline{\omega }_{\ell } = \left( {\int\limits_{0}^{R} {\left| {{\mathop{u}\limits^{\rightharpoonup}}_{{\theta }} } \right|dr} } \right)/R^{2}$, was used to modify the effective frequency of the magnetic field, $f_{{{\text{eff}}}}$$= {{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} {2\pi }}} \right. \kern-\nulldelimiterspace} {2\pi }}$. The effect of the liquid flow on the generated $Q_{{\text{J}}}$ can also be considered with this method.

A two-way coupling between EM and CFD solvers (Calculation method 3) is possible, but the iteration scheme should be established manually. Before the activation of RMF, the liquid is assumed stationary, i.e., $\overline{\omega }_{\ell ,0} = 0$, f_eff = f, and $\omega_{{\text{B}}} = 2\pi f_{{}}$. These are the initial conditions for the first EM calculation between the EM–CFD iteration. Then, the calculated ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$, with the $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$ modification, is used for the first CFD calculation. Typically, the calculated angular velocity of the liquid ($\omega_{\ell }$ = $\left| {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}}_{\theta } } \right|$/r) is not uniform because $u_{{\theta }}$ is not linearly distributed along the radius. Hence, the averaged angular velocity $\overline{\omega }_{\ell }$ was used to characterize the angular flow. Based on this, the effective rotation frequency of $\mathop{B}\limits^{\rightharpoonup}$ field is obtained, $f_{{{\text{eff}}}} = \frac{{\omega_{{\text{B}}} - \overline{\omega }_{\ell } }}{2\pi }$. Hence, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ can be updated in the next EM–CFD iteration based on the obtained $f_{{{\text{eff}}}}$. As shown in Figure 2(c), further iterations are made until $\left| {\Delta \overline{\omega }_{\ell } /\overline{\omega }_{\ell } } \right|$< 5 pct, and then the iteration is terminated, where $\left| {\Delta \overline{\omega }_{\ell } } \right|$ denotes the difference of the averaged angular velocity $\overline{\omega }_{\ell }$ between two sequent iterations. It should be noted that the criterion of 5 pct is arbitrarily set, but it can be modified for other simulations when higher accuracy is demanded.

As shown in Figure 1(a), a full-scale inductor was developed to perform EM calculation. The sample is placed at the middle height of the inductor. Eddy current ($\mathop{J}\limits^{\rightharpoonup}$) was considered only in the conductive sample. When a three-phase AC is excited on the three windings, a primary rotating magnetic field can be induced. Given that the current inductor has one pair of poles, the frequency of the magnetic field is the same as the frequency of the applied current. Based on Faraday's law, the $\mathop{J}\limits^{\rightharpoonup}$-induced magnetic field opposes the change in the primary rotating magnetic field. The interaction between the total $\mathop{B}\limits^{\rightharpoonup}$ and $\mathop{J}\limits^{\rightharpoonup}$ produces the Lorentz force (${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$). The strength of electric field ($\mathop{E}\limits^{\rightharpoonup}$) can be calculated as follows:

$$ \nabla \times \mathop{E}\limits^{\rightharpoonup} = - \frac{{\partial \mathop{B}\limits^{\rightharpoonup} }}{\partial t}. $$

(1)

The strength of the induced $\mathop{J}\limits^{\rightharpoonup}$ can be calculated as follows:

$$ \mathop{J}\limits^{\rightharpoonup} = \sigma (\mathop{E}\limits^{\rightharpoonup} + \mathop{u}\limits^{\rightharpoonup} \times \mathop{B}\limits^{\rightharpoonup} ), $$

(2)

where $\mathop{u}\limits^{\rightharpoonup}$ denotes the liquid velocity of the sample. Specifically, $\mathop{u}\limits^{\rightharpoonup}$ is set as zero for the case of solid sample (torque measurement) or it is calculated according to the averaged $\overline{\omega }_{\ell }$ for the case of liquid sample. The Lorentz force exerted on the sample can be calculated as follows:

$$ {\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}} = \frac{1}{2}R_{e} (\mathop{J}\limits^{\rightharpoonup} \times \mathop{B}\limits^{\rightharpoonup} ), $$

(3)

where R_e denotes the real part of a complex number. The torque on the solid sample is given by

$$ \mathop{\tau }\limits^{\rightharpoonup} = \frac{1}{2\pi }\int_{0}^{2\pi } {\left\{ {\int\limits_{Vol} {\mathop{r}\limits^{\rightharpoonup} \times \left( {\mathop{J}\limits^{\rightharpoonup} \times \mathop{B}\limits^{\rightharpoonup} } \right)dV} } \right\}} d\theta . $$

(4)

In the current study, the transient 3D flow was calculated. Further assumptions were made as follows:

• (1) The Joule heat is neglected during the CFD calculation.

• (2) The secondary (and higher order of) eddy current in the EM calculation is not considered.

• (3) The liquid alloy is incompressible and isothermal with constant density and viscosity.

• (4) In the CFD calculation, a so-called course-grid direct numerical simulation is conducted, i.e., no turbulence model is used.

• (5) All walls of the crucible are assumed to be no-slip.

Among all eight experiment cases in Table II, only Case (3) (f = 50 Hz, R = 12.5 mm) is analyzed numerically in detail. The alloy (Ga75In25) is confined in a cylindrical crucible with H = 100.0 and R = 12.5 mm. The sample is enmeshed into 8.5 × 10⁵ hexahedral elements with maximum mesh size of 400 µm. $\Delta t$ for the first and third calculation method is 1 × 10⁻³ s, and a smaller $\Delta t$ of 5 × 10⁻⁵ s is used for the second calculation method due to the spatial and temporal interpolation of the rotating ${\mathop{B}\limits^{\rightharpoonup}}_{0}$. As listed in Table III, four simulations are conducted with different RMF intensities. The material properties and other parameters are summarized in Table IV.

Table III Simulations Performed for the Model Alloy (Ga75In25)

Table IV Summary of Material Properties and Other Parameters*

Experimental Results and Model Evaluations

Magnetic Induction

The magnetic induction is calculated via the EM solver ANSYS Maxwell, Figure 2(c). With the three-phase AC (I = 5700 A, f = 50 Hz), a rotating $\mathop{B}\limits^{\rightharpoonup}$ is induced. The calculated $\mathop{B}\limits^{\rightharpoonup}$ on the plane of middle height of the inductor at a phase of 300° is shown in Figure 3(a). The maximal $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ (1650 mT) is realized in the iron core, while $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ at the inductor center is an order of magnitude smaller. The calculated $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the axis of the inductor (the red vertical line in Figure 3(a)) for the case without sample loading matches the experimental measurements quite well, Figure 3(b). In this paper, the calculated $\mathop{B}\limits^{\rightharpoonup}$ field without sample loading is served as the input ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ field in calculation method 2, Figure 2(b). When a copper sample (H =150 mm, R = 10 mm) is loaded, the $\mathop{B}\limits^{\rightharpoonup}$ field in the sample is subject to the skin effect. As displayed by the black dash line in Figure 3(b), the calculated $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the axis of the sample should be reduced by approximately 13 mT. However, there is no measurement data for this case. Furthermore, $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the blue circle (R = 10 mm) for the case without sample loading, as denoted in Figure 3(a), is measured and compared with the calculation results in Figure 3(c). The experiment and calculation results are in excellent agreement, and a constant/uniform $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ (160 mT) is obtained.

Fig. 3

Experiment–simulation comparison of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ for the case with f = 50 Hz, I = 5700 A. (a) Calculated $\mathop{B}\limits^{\rightharpoonup}$ on the plane of middle height of the inductor at a phase of 300°. (b) $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the axis of the inductor. (c) $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the blue circle as marked in (a)

Torque

The magnetic torque ($\tau$) is also calculated via the EM solver ANSYS Maxwell, Figure 2(c). The calculated $\tau$ for solid samples of three metal/alloys (Table I) as a function of $\mathop{B}\limits^{\rightharpoonup}$ is compared with those obtained via experiments as shown in Figure 4. For all samples, $\tau$ increases exponentially with $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$. The simulation results are in excellent agreement with the measurements. Given the difference in electronic conductivities, as listed in Table IV, the torque of Cu is the highest, followed by Al and AlSi7.

Fig. 4

Comparison of $\tau$ on different samples

RMF-Driven Liquid Flow

Different simulation cases (Table III) exhibit similar flow pattern when they are calculated with different calculation methods (Figure 2). Only the results of Simulation C, which are calculated using calculation method 3 (Figure 2(c)) after 3 EM–CFD iterations, are presented in Figure 5. According to Figure 6, the calculation gets converged after 3 EM–CFD iterations. The liquid flow is dominated by the rotating toroidal flow (${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$), which exhibits the same magnitude with ${\mathop{u}\limits^{\rightharpoonup}}_{\ell }$ ($\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{\ell } } \right| = \sqrt {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}}_{\theta }^{2} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}_{\psi }^{2} }$). As shown in Figures 5(a) and (b), a strong rotating flow up to the magnitude of 1.2 m/s was induced in the sample, while the induced secondary poloidal flow (${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$) is approximately one magnitude lower. Furthermore, as shown in Figure 5(c), ${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$ is characterized by those intermittent tubes, but ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ is chaotic and is characterized by the prevailing of multiple Taylor–Görtler (T–G) vortices.^[11,41] Most of the T–G vortices are observed near the sample surface. They originate randomly around those tubes, and then increase in size, coalesce with neighboring ones, or even split into sub-vortex. Simultaneously, they move up and downward. Finally, they dissipate near the top and bottom wall (the so-called Bödewadt/Ekman layer^[2,41]). The vertical motion of these T–G vortices transports the angular momentum. According to Figure 5(c), a few of the vortices can also be observed in the central area. Although they exhibit similar features to the vortex near the sample surface, their nucleation frequency and survival number density are much lower. These vortices are responsible for the slow velocity oscillation along the axis, Figure 5(a). The total pressure P_Total, excluding the hydrostatic pressure ($P^{\prime} = \rho gh$), is demonstrated in Figure 5(d). The maximum of P_Total is located in the range of 0.5 to 1.0 mm to the surface. This result is consistent with our previous experimental observation.^[39]

Fig. 5

Calculated results of Simulation C of Table III at t = 20 s. (a) $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{{\theta }} } \right|$ on a symmetry plane; (b) $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{{\psi }} } \right|$ on a symmetry plane, (c) vectors of ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ on a symmetry plane together with one 3D iso-surface of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{{\theta }} } \right| = 1.2{\text{ m/s}}$, and the thick red vector (zoomed section) indicates the flow direction of azimuthal flow; (d) Counter of total pressure P_Total excluding the hydrostatic pressure (Color figure online)

Fig. 6

Convergence analysis of EM–CFD coupling scheme. (a) Evolution of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$ at a reference point (as denoted in Fig. 5(a)) for Simulation C ($\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ = 28 mT, R = 12.5 mm), and the curves with different colors (black, red, and blue) indicate the calculated velocities corresponding to three sequent iterations; (b) Calculated $\overline{\omega }_{\ell }$ of different simulation cases during the iteration scheme; (c) Necessary EM–CFD iteration numbers, required to satisfy the criterion $\left| {\Delta \overline{\omega }_{\ell } /\overline{\omega }_{\ell } } \right|$< 5 pct, as a function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ (Color figure online)

To analyze the convergence behavior of EM–CFD coupling scheme, the evolution of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$ at a reference point (mid-height of the sample and 2.5 mm to the sample surface as denoted by the black spot in Figure 5(a)) during different EM–CFD iterations is plotted in Figure 6(a). According to the EM–CFD coupling scheme in Figure 2(c), the first EM simulation is conducted by assuming that the liquid melt in the sample is stationary ($\overline{\omega }_{\ell }$= 0, i.e., $f_{{{\text{eff}}}}$= 50 Hz) such that maximum ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is generated. As a consequence, the maximum of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$ (or the maximum $\overline{\omega }_{\ell }$), i.e., the black line in Figure 6(a), is obtained. It should be noted that the high-frequency oscillation of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$ is not due to numerical iterations, but due to the prevailing T–G vortices, which are observed in Figure 5(c). For the second iteration of the EM simulation, $f_{{{\text{eff}}}}$ is updated as (${{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} {2\pi }}} \right. \kern-\nulldelimiterspace} {2\pi }}$). Hence, a reduced ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is obtained, and in turn a reduced $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$, i.e., the red line in Figure 6(a), is obtained. Following the further EM–CFD coupling scheme, $f_{{{\text{eff}}}}$ is updated again, and a new $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$ is obtained with further EM–CFD iterations. The iteration is terminated when the convergence criterion $\left| {\Delta \overline{\omega }_{\ell } /\overline{\omega }_{\ell } } \right|$< 5 pct is satisfied. The calculated $\overline{\omega }_{\ell }$ of different simulation cases (Table III) following the iteration scheme is displayed in Figure 6(b). As mentioned previously, only Case 3 (R = 12.5 mm, f = 50 Hz) of Table II is analyzed in detail. The simulations are in good agreement with the experimental results, but more iterations between the EM and CFD calculations are required with an increase in $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$. Figure 6(c) shows the necessary EM–CFD iteration numbers as a function of the RMF intensity ($\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$). When $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ is low, e.g., Simulation A and B, no iteration is required to obtain results close to the experiment, while 2 and 4 iterations are required for simulations C and D to converge to the experimental results, respectively. For the current experiment configuration, when $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ < 28 mT, the accuracy of the simulation results can be accepted without any iteration, while iterations are required when $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ ≥ 28 mT. Therefore, we divide Figure 6(c) into two regions (green vs. red) with critical $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ = 28 mT.

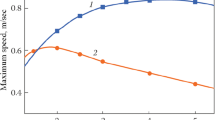
The experimentally measured RMF-driven rotating angular velocity $\overline{\omega }_{\ell }$ in the liquid sample as a function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ is shown in Figure 7(a). Within the measured range of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$, $\overline{\omega }_{\ell }$ of all experimental cases show almost a linear function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$. It should be noted that with an increase in $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$, $\overline{\omega }_{\ell }$ approaches closer and closer to $\omega_{{\text{B}}}$, but it can never reach $\omega_{{\text{B}}}$. The calculated $\overline{\omega }_{\ell }$ as a function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ with different methods and modification strategies is shown in Figure 7(b). Specifically, $\overline{\omega }_{\ell }$ is calculated via $\overline{\omega }_{\ell } = \left( {\int\limits_{0}^{R} {u_{{\theta }} dr} } \right)/R$. With the first calculation method (Figure 2(a)), as shown by the green line in Figure 7(b), $\overline{\omega }_{\ell }$ is considerably overestimated. By referring to simulation C ($\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ = 28.0 mT), the calculated $\overline{\omega }_{\ell }$ is overestimated by ca. 34.4 pct. With the second calculation method (Figure 2(b)), as demonstrated by the black line and squares in Figure 7(b), $\overline{\omega }_{\ell }$ shows good agreement with the experimental measurements. With the third calculation method (Figure 2(c)), different modification strategies were performed to check their effect on the calculation accuracy. In Figure 7(b), the blue line indicates the calculated $\overline{\omega }_{\ell }$ using the EM–CFD iteration scheme without any modification and iteration, red line indicates the calculated $\overline{\omega }_{\ell }$ by solely using the EM–CFD iteration scheme with the modification $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$ but without any iteration, and pink line indicates the calculated $\overline{\omega }_{\ell }$ using the EM–CFD iteration scheme with the modification by $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$ and iteration. Evidently, $\overline{\omega }_{\ell }$ differs significantly if modification strategies of ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ are varied. The calculated $\overline{\omega }_{\ell }$ is overestimated by ca. 66.2 pct without any modification and iteration. If ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is solely modified by a factor of $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$, $\overline{\omega }_{\ell }$ is overestimated by ca. 29.6 pct. Hence, only when the modification and iteration are conducted, $\overline{\omega }_{\ell }$ can reproduce the experimental results.

Fig. 7

(a) Measured angular velocities as a function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ for all eight experiment cases as defined in Table II; (b) Comparison between simulations and experiments for Case 3 (R = 12.5 mm, f = 50 Hz). The experimental results are reprinted from Ref. [39], under the terms of the Creative Commons CC BY license

Application in Continuous Casting Process

The methodology, as introduced in this study, was used to study the effect of M-EMS on the superheat dissipation and the formation of as-cast structure in a billet CC casting (195 × 195 mm²) via a three-phase mixed columnar-equiaxed solidification model.^[42,43] The three phases correspond to the steel melt, columnar dendrites from which the steel shell is fabricated, and equiaxed crystals, which are treated as an additional disperse continuum solid phase as schematically shown in Figure 8(a). Their volume fractions correspond to $f_{\ell } , \, f_{{\text{c}}} , \, f_{{\text{e}}}$. The growth kinetics for the columnar dendrites and movable equiaxed crystals are considered. The origins of the equiaxed crystals by the mechanisms of crystal fragmentation and heterogeneous nucleation are included. Furthermore, remelting and destruction of the equiaxed crystals in the superheated and/or oversaturated liquid are also considered. The details of the model and implementation of model can be referred to in References 42 and 43. Only the simulation results related to M-EMS near the mold region are analyzed in this study.

Fig. 8

A mixed columnar–equiaxed solidification model is used to simulate the as-cast structure formation in a CC billet casting under the effect of M-EMS. (a) Schematic of mixed columnar–equiaxed solidification model; (b) Layout of the M-EMS stirrer (inductor); (c) Contour of $\left| {{\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}} } \right|$ on the vertical section of the strand; (d) Vector of ${\mathop{u}\limits^{\rightharpoonup}}_{\ell }$ on an 3D iso-surface of $\left| {{\mathop{u}\limits^{\rightharpoonup}}_{\ell } } \right|$= 0.08 m/s; (e) Contour of volume fraction of columnar phase (f_c) overlaid by the vectors of ${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$ (vertical section) and ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ (cross section) of the liquid; (f) Contour of volume fraction of equiaxed phase (f_e) overlaid by the vectors of ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ of the equiaxed crystals on the vertical section; (g) Contour of $\omega_{\ell } /\omega_{{\text{B}}}$ on the vertical section

The M-EMS is created by a two-pole inductor with a three-phase AC, Figure 8(b). $\left| {{\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}} } \right|$ is shown on a symmetry section of the strand, Figure 8(c). The maximum $\left| {{\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}} } \right|$ of 6000 N/m⁻³ appears at the strand surface. It should be stressed that during the solidification and flow simulation, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is modified by multiplying ($1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }}$) to consider the relative motion between the melt and $\mathop{B}\limits^{\rightharpoonup}$, i.e.,$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F} ^{\prime}_{{\text{L}}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F} _{{\text{L}}}^{{}} (1 - {{\omega _{\ell } } \mathord{\left/ {\vphantom {{\omega _{\ell } } {\omega _{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega _{{\text{B}}} }})$. Additionally, due to the multiphase nature of the solidification, the total effective $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}^{\prime}_{{\text{L}}}$ must be partitioned among three phases according to their volume fractions, i.e.,$f_{\ell } {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$, $f_{{\text{e}}} {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$, and $f_{{\text{c}}} {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$. They are the corresponding source terms for the momentum equations. A relatively strong rotating liquid flow is induced in the mold region by M-EMS, as depicted in Figure 8(d). The strongest liquid flow is obtained at the position several centimeters above the middle height of the stirrer (inductor). This is attributed to the thickening of the shell along the casting direction. This liquid flow ${\mathop{u}\limits^{\rightharpoonup}}_{\ell }$ is composed of the azimuthal flow ${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$ and secondary (radial and axial) flow ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$, which can be observed on the cross section and vertical section of the strand, respectively, in Figure 8(e). According to References 14 and 29, ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ is due to the imbalance in the radial pressure gradient owing to the centrifugal force. This differs from the laboratory case, Figure 5, wherein ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ is characterized by the two pairs of recirculation loops above and below the stirrer center. The upper recirculation loop inhibits the downward flow of the melt coming from the side ports of the submerged entry nozzle (SEN), and a small part of the melt is blocked near the SEN, Figure 8(e). The interaction between ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$ with the jet flow coming from the downward port of the SEN strengthens the upper pair of recirculation loop. However, this downward flow is still weaker than ${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$. Despite its low intensity, a consensus is that the transport of heat and mass in the casting is dominated by ${\mathop{u}\limits^{\rightharpoonup}}_{{\psi }}$.^{[14,19,29,44]} Figure 8(f) shows that the motion of equiaxed crystals exhibits the same pattern as the melt flow. If the crystals are transported to the superheated region, then they can be remelted and even destroyed. The ratio between the rotating angular velocity of the liquid to $\mathop{B}\limits^{\rightharpoonup}$ ($\omega_{\ell } /\omega_{{\text{B}}}$) is shown in Figure 8(g). Given that $\omega_{\ell }$ is not uniform along the axis direction of the strand, the suggested EM–CFD iteration scheme cannot be directly applied to this CC case. This implies that the flow in the center mold region can be slightly overestimated.

To demonstrate the feasibility of the proposed method for M-EMS in CC billet, the calculated temperature distribution on the surface of the strand, the calculated phase distribution on a cross section of as-solidified strand, and a macrograph of the as-cast structure (field experiment) are shown in Figure 9. It is verified that the numerical model can reproduce the experimental results successfully. Based on our previous study,^[42] the main functionalities of the M-EMS are (1) to promote the formation of crystal fragments via the mechanism of fragmentation; (2) to disperse the superheat in the mold region, leaving the lower region beneath the mold undercooled; and (3) to allow the crystal fragments to survive and continue to grow in the undercooled region, and thereby, to form the equiaxed structure in the core region of the strand.

Fig. 9

(a) Calculated temperature distribution on the surface of the strand; (b) Calculated distribution of f_e overlaid by two isolines to indicate different macrostructures. (c) Macrograph of the as-cast structure of the strand (field experiment). (b) and (c) are reprinted from Ref. 42, under the terms of the Creative Commons CC BY license (https://creativecommons.org/licenses/by/4.0/)

Discussion

Evaluation of Different Iteration/Simplification Schemes

During the MHD calculation, there are two main points that should be carefully treated, i.e., the eddy current effect and relative motion between the liquid and $\mathop{B}\limits^{\rightharpoonup}$. As shown in Figure 3(b), once a conductive sample is loaded, $\mathop{B}\limits^{\rightharpoonup}$ is updated by the eddy current. The slip motion between the liquid and $\mathop{B}\limits^{\rightharpoonup}$ field modifies the effective frequency $f_{{{\text{eff}}}}$. As mentioned in § 3, $f_{{{\text{eff}}}}$ decreases with $\overline{\omega }_{\ell }$ following $f_{{{\text{eff}}}} = {{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{{\text{B}}} - \overline{\omega }_{\ell } } \right)} {2\pi }}} \right. \kern-\nulldelimiterspace} {2\pi }}$. The analytical solution, Figure 2(a), cannot account for the eddy effect and end effect. The effect of liquid rotating on $f_{{{\text{eff}}}}$ can only be considered one-way by a factor of $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$. Given these simplifications, as demonstrated in Figure 7(b), the calculated $\overline{\omega }_{\ell }$ is considerably overestimated. The eddy effect and slip motion can be iteratively solved by using the coupled simulation via ANSYS Fluent addon MHD module, Figure 2(b), which ensures high calculation accuracy at the expense of excessive computation time. Given the demanded small $\Delta t$, this method is limited to simple cases as opposed to the multiphase solidification simulations of CC process. If the MHD calculation is performed with the third calculation method, Figure 2(c), then the calculation accuracy is highly dependent on the modification strategies. From Figure 7(b), it can be observed that if the coupling between $\overline{\omega }_{\ell }$ and ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is neglected, i.e., the blue line, then it leads to unacceptable simulation results. Nevertheless, this de-coupled method was adopted in many simulations.^{[9,18,21,31,32,33,34,37,45]}

Different solutions exhibit different computational costs. For the case with B = 28 mT and f = 50 Hz, which were run on a high-performance cluster (2.6 GHz, 12 cores), to reach a quasi-steady state, the analytical solution (Figure 2(a)) took four days ($\Delta t$ = 1 × 10⁻³ s); the second method, Figure 2(b), took about ten days ($\Delta t$ = 5 × 10⁻⁵ s); depending on the modification strategies of the third method, Figure 2(c), one to two weeks was needed ($\Delta t$ = 1×10⁻³ s). For the third solution, if ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was only modified by multiplying ($1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }}$) but without any iteration, i.e., the red line in Figure 7(b), it took about one week.

Although the simulations are in good agreement with the experimental measurements after several EM–CFD iterations (pink line in Figure 7(b)), it should be noted that $\overline{\omega }_{\ell }$ was used to approximate $\omega_{\ell }$ during each EM–CFD iteration. With the increase in ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$, the flow becomes more chaotic, and ${\mathop{u}\limits^{\rightharpoonup}}_{{\theta }}$ becomes more non-linear along the radius of the sample. In this case, $\overline{\omega }_{\ell }$ can potentially not characterize the overall flow correctly. This decreases the accuracy of this approach. Given that $\omega_{\ell }$ is not uniform along the axis direction of the strand during the CC process, Figure 8(g), the suggested EM–CFD iteration scheme cannot be fully applied. However, the following was realized. (1) ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ was modified by multiplying ($1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }}$) to consider the relative motion between the melt and $\mathop{B}\limits^{\rightharpoonup}$, and (2) ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}{^{\prime}}$ was partitioned among three phases according to their volume fractions. Based on Figure 8(g), the overestimated melt flow is enclosed in a short and narrow core of the casting. This implies that this slight overestimation should not significantly impact the as-cast structure.

Analytical Solution for EMS

The analytical formulae were derived based on an infinite cylinder to approximate the time-averaged ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$.^[27,29,40] In a cylindrical coordinate system, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is composed of ${\mathop{F}\limits^{\rightharpoonup}}_{{\theta }}$, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{r}}}$, and ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{Z}}}$. In the case of a uniform magnetic field rotating about a long cylinder, ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{Z}}}$ is shown to be zero.^[29,40] The expressions for ${\mathop{F}\limits^{\rightharpoonup}}_{{\theta }}$ and ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{r}}}$ can be observed in Figure 2(a) wherein $\mu_{0}$ (=$4\pi \times 10^{ - 7} {\text{H/m}}$) denotes the electrical permeability of free space, and $f(z)$ denotes a distribution function of $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ along the axial direction of the inductor. If the inductor height is infinite relative to the casting, $\mathop{B}\limits^{\rightharpoonup}$ can be presumed as uniformly distributed along the height direction, i.e., $f(z)$=1.^[19,26,46] Regarding the CC process, the stirrer is significantly shorter than the casting. Generally, $f(z)$ is obtained by fitting the measured $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$.^[27,30,40] An example for $f(z)$ is also shown in Figure 2(a) wherein $z_{{{\text{mid}}}}$ denotes the middle position of the stirrer, and $z_{{{\text{width}}}}$ denotes the effective width of the $\mathop{B}\limits^{\rightharpoonup}$ field. This analytical solution can also be applied to the CC process of billet and bloom by reverting the length (a) and width (b) of the casting cross section to an equivalent radius via $R_{{\text{e}}} { = 2}\sqrt {\frac{ab}{\pi }}$.^[27] As discussed in § 6.1, the liquid flow can be overestimated with this method. The Joule heat ($Q_{{\text{J}}}$) can also be analytically approximated, and the formula for $Q_{{\text{J}}}$ is obtained from a previous study.^[27]

Other Issues for EMS and Outlook

One of the main objectives of this study was to quantify the accuracy of different modification strategies and emphasize certain necessary modifications on ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$, which are summarized as below:

• (1) The analytical solution (Figure 2(a)), relying on its calculation efficiency and easy implementation, is an alternative option to obtain acceptable simulation results. An extra EM solver is not required, but $\mathop{B}\limits^{\rightharpoonup}$ field should be known in advance via other measurement or calculation method. With this one-way coupling method, the main drawback involves neglecting the eddy effect. As pronounced by Spitzer et al.,^[29] this analytical solution is accurate for $R_{{\text{m}}} \le {3}$ ($R_{{\text{m}}} = \omega_{{\text{B}}} \sigma \mu_{0} R^{2}$). Furthermore, the influence of the solidified shell,^[42] mold temperature,^[42] liquid flow, and the formation of air gap between the casting the mold^[47] on $\mathop{B}\limits^{\rightharpoonup}$ field cannot be considered. When this method is applied to continuous castings (billet, bloom, or slab), the converted equivalent radius via $R_{{\text{e}}} { = 2}\sqrt {\frac{ab}{\pi }}$ can also lead to significant discrepancy.

• (2) The ANSYS Fluent addon MHD module (Figure 2(b)) provides a coupled calculation scheme, but ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ must be provided either by EM calculation or physical measurement. Because of the explicit temporal resolution of ${\mathop{B}\limits^{\rightharpoonup}}_{0}$, $\Delta t$ should be very small.^[24] Based on the frequency of ${\mathop{B}\limits^{\rightharpoonup}}_{0}$ (3–50 Hz), $\Delta t$ can be varied in the range of 10^-4 to 10⁻⁵ s. The additional solving of $\mathop{b}\limits^{\rightharpoonup}$ equations and their interaction with the momentum equations and energy equations significantly decrease the speed of the calculation, and this in turn poses challenges for the simulation to converge. According to the simulation results, $\left| {\mathop{b}\limits^{\rightharpoonup} } \right|$ is about 10 pct of $\left| {{\mathop{B}\limits^{\rightharpoonup}}_{0} } \right|$ for the currently studied laboratory scale casting, e.g., $\left| {\mathop{b}\limits^{\rightharpoonup} } \right|$ =0.53 mT for $\left| {{\mathop{B}\limits^{\rightharpoonup}}_{0} } \right|$ =5.6 mT, and $\left| {\mathop{b}\limits^{\rightharpoonup} } \right|$ =2.1 mT for $\left| {{\mathop{B}\limits^{\rightharpoonup}}_{0} } \right|$ =28 mT. It should be noted that this additional MHD module is not compatible with the Eulerian–Eulerian multiphase approach in ANSYS Fluent on which most advanced solidification models have been developed.

• (3) If ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ is calculated by an external EM solver, then it is possible to consider all the aforementioned effects, including the eddy effect, formation of air gap between casting and mold,^[47] insulating/conducting wall boundary conditions,^[42] temperature-dependent electrical conductivities,^[42] and different mold temperatures.^[32] There are even more possibilities to perform parameter study on $\mathop{B}\limits^{\rightharpoonup}$. As demonstrated in Figure 7(b), terming the calculated ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ directly as the source force without any modifications leads to the unacceptable calculated flow field.^[24] We do not recommend using the currently proposed EM–CFD iterative scheme in the simulations of CC process, but the modification of ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ by a factor of $(1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$ is necessary and can improve the calculation accuracy considerably. It should be stated that the currently proposed EM–CFD iteration scheme provides one option for Eulerian–Eulerian multiphase simulation to improve the calculation accuracy.

It is known that the casting size/geometry can also affect the EMS-driven flow. However, performing velocity measurements on the engineering continuous casting is not possible. In addition to the current benchmark, there is a middle-scale facility which was built in Dresden.^[15] The sample size is 800 mm in length and 80 mm in diameter. The cold liquid metal (Ga₆₈In₂₀Sn₁₂) in the casting mold was stirred by a rotary electromagnetic field. The melt, as injected from the SEN into the mold, interacts with the RMF-driven flow. The fluid rotating velocities under different $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ (4.1 to 18.3 mT) were measured via ultrasound doppler velocimetry technique. As an additional step, the scaling effect should be investigated based on the current laboratory benchmark and middle-scale physical model.

Summary

An experiment benchmark was presented to verify the MHD methods that were typically used for investigation of the flow and solidification during continuous casting (CC) process. A two-pole inductor charged by a three-phase AC was developed to generate a rotating magnetic field (RMF) with variable $\left| {\mathop{B}\limits^{\rightharpoonup} } \right|$ and f. Systematic data, including the magnetic field, torque, and RMF-driven liquid flow, were provided.

Three typically used MHD methods for CC process were evaluated via comparison with the experiment data set. The analytical solution for the ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ corresponded to easy-to-implement method with highest computation efficiency, but it was limited to the low-frequency cases, and the liquid velocity can be considerably overestimated because the eddy effect was ignored. The ANSYS Fluent addon MHD module provided the highest calculation accuracy, but there were drawbacks of excessively high computation cost, incompatibility for multiphase solidification problem, and the external magnetic field should be measured or calculated elsewhere. The third method involves combining the EM and CFD calculations between ANSYS Maxwell and ANSYS Fluent. To ensure the calculation accuracy by considering the eddy current and flow effect on the EM field, an iteration scheme was proposed. As the iteration was conducted manually, it was not feasible for industry CC.

Although the EM–CFD iteration is not recommended for the CC process, necessary calculation accuracy can still be realized by this scheme without iteration. However, additional modifications to ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}$ must be carefully considered in the CFD and solidification calculation. The relative motion between the melt and $\mathop{B}\limits^{\rightharpoonup}$ field should be considered by ${\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}}{^{\prime}} = {\mathop{F}\limits^{\rightharpoonup}}_{{\text{L}}} (1 - {{\omega_{\ell } } \mathord{\left/ {\vphantom {{\omega_{\ell } } {\omega_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {\omega_{{\text{B}}} }})$. Finally, due to the multiphase nature of solidification during CC, the ${\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$ must be further partitioned among different phases (liquid, equiaxed, and columnar) according to their volume fractions, i.e., $f_{\ell } {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$, $f_{{\text{e}}} {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$, and $f_{{\text{c}}} {\mathop{F}\limits^{\rightharpoonup}}^{\prime}_{{\text{L}}}$.