Mathematical Modeling of Furnace Drainage While Tapping Slag and Metal Through a Single Tap-Hole

Abstract

Furnace tapping is a critical operation on pyrometallurgical furnaces known for unpredictable performance in many cases. A reduced order mathematical model capable of predicting tapping rates of both slag and metal is presented. The model accounts for separate liquid phases and particle bed resistance to flow. The model is compared for consistency against results from both a water-model experiment and computational fluid dynamics simulations. The model is applied to study drainage from a typical ferro-manganese furnace. The model results show that particle bed conditions in the immediate vicinity of the tap-hole strongly influence tapping rates and that the slag/metal interface deformation due to suction pressure near to the tap-hole is significant and must be accounted for in such models.

Introduction

Tapping is the process of transferring molten materials from a pyrometallurgical furnace into a ladle, as illustrated in Figure 1. Tapping is governed by the physics of fluid drainage, and its performance is sensitive to a number of furnace operating conditions and material properties. An understanding of the governing mechanisms behind furnace tapping is vital for estimating material flow all the way to the final product. In order to extract molten products from a furnace with minimum disruption to the metallurgical process, the tapping rates should always match the production rates of the furnace as closely as possible. However, this is not always the case on operating furnace plants, and the reasons for this can be unveiled by mathematical models. Although the governing equations for drainage from tap-holes are similar between furnaces, there are any number of possible variations in tapping configurations including single or multiple tap-holes, single phase or multiple phases, continuous or discontinuous tapping, and other differences.[1] Here we focus on a mathematical model for simultaneous tapping of slag and metal through a single tap-hole as exemplified by the tapping of submerged-arc furnaces used in the production of manganese ferro-alloys.

Fig. 1

Illustration of tapping process

Ferro-alloy furnaces are geometrically and phenomenologically complex unit operations. Common features across different commodities include the presence of a molten bath consisting of at least two liquid phases, typically a lighter oxide-rich slag and a denser metallic alloy. A granular burden layer is located above the molten bath and contains a mixture of solid ore, flux, and carbonaceous reductant particles. This porous burden layer may also penetrate one or both of the molten phases, in which case it is generally enriched in reductants and is referred to as a “wet coke bed.” The furnace interior may exhibit very different structure depending on the process—in silico-manganese and ferro-silicon furnaces an open cavity with an electric arc is normally present beneath each of the three electrodes, while in ferro-manganese and ferro-chromium processes either a dry or wet coke bed in contact with the electrodes supplements conduction of electricity through the process material.[2] Away from the electrodes in the vicinity of the furnace tap-hole however, a wet coke bed is generally present in all ferro-alloy processes.[3,4,5,6,7]

Furnace tapping is conceptually similar to drainage of tanks, a simple engineering problem which is often used as a modeling example in introductory classes in fluid mechanics and mathematics to illustrate the basic principles of pressure-driven flow and as an example of first-order differential equations (e.g., Reference 8). Compared to the canonical tank drainage problem, furnace tapping is complicated by the presence of more than one liquid phase and a packed bed of granular material formed by the burden layer. The packed bed provides resistance to drainage and this needs to be accounted for in mathematical models for furnace tapping.

Drainage models for single liquid systems without a packed bed apply Bernoulli’s principle of conservation of mechanical energy. This gives an analytical solution for the drainage rate as a function of liquid level, which produces the hydrostatic pressure that is the driving force of the drainage. This concept is also applicable to furnace tapping, and has been explored for blast furnaces. Nouchi et al.[9] derived a model based on Bernoulli’s principle and demonstrated the importance of a coke free (i.e., particle free) zone close to the tap-hole. In their model, the presence of two liquid phases in the tapping stream was accounted for by a mixture model, in which averaged material properties are calculated based on the quantities of slag and metal present. This allows a total tapping flowrate for the mixture to be estimated using the standard equations for single phase flow. The same model was applied by Iida et al.[10] to study a low permeability zone in the furnace hearth. Shao and Saxén[11] derived a two-fluid drainage model for blast furnaces where the slag and metal were treated as separate immiscible phases. Their model allowed for the independent computation of tapping rates for each phase. The model concept for blast furnaces has also been adapted to submerged-arc furnaces for production of manganese alloys; an example of this is shown in Muller et al.[12] Their work was based on the mixture model concept of Iida et al.[10]In all of the mentioned work on drainage models, the Kozeny–Carman equation,[13,14] which is applicable to laminar flow only, is applied to model the pressure loss due to the particle bed.

Here we apply the two-fluid approach with separated phases[11] to submerged-arc furnaces and tapping of ferro-manganese. The model is enhanced by introducing a correlation for the pressure drop in the particle bed accounting for turbulence, and including the effect of deformation of the slag/metal and slag/gas interphases toward the tap-hole. Note that such modeling capabilities (and the ability to study more complex furnace conditions) are already available through computational fluid dynamics (CFD). Although such detailed models can offer great insight into tapping behavior, they are computationally expensive and often prohibitively time-consuming to run. With a simplified reduced order model of the furnace and tap-hole based on Bernoulli’s principle, large numbers of tapping calculations can be performed rapidly for use in broader process parameterization and sensitivity studies. The reduced order model then becomes a pragmatic alternative to computational methods for cases in which computational speed is more important than high levels of detail or accuracy.

Model Development

Furnace tapping of slag and metal is described geometrically by the height of the slag–metal interface h_m, slag–gas interface h_s and the tap-hole centerline h_t, relative to the bottom of the furnace. The diameter of the tap-hole is given by d_t. Due to the creation of a low-pressure suction region at the tapping channel entrance, the fluid interfaces may deform toward the tap-hole (this effect is also observed when draining a kitchen sink, for example). In a furnace with multiple liquid phases present, the deformation of the interfaces is an important effect required to account for the fact that tapping of the upper liquid can start even though the average level of the interface is still above the tap-hole. Thus, the interface level at the tap-hole entrance differs from that at the furnace center. The deformed interface level is given by h_out. Figure 2 illustrates different stages of tapping with different interface deformations.

Fig. 2

Two-phase tapping of furnace with high liquid levels (a), medium levels (b), and low levels (c)

In the metal phase, Bernoulli’s principle for a streamline from the metal surface (i.e., slag/metal interface) to the tap-hole outlet yields

$$ P_{\text{m}} - \Delta P_{\text{pb,m}} - \Delta P_{t} + \rho_{\text{m}} gh_{\text{m}} + \frac{1}{2}\rho_{\text{m}} v_{\text{m}}^{2} = P_{\text{out}} + \rho_{\text{m}} gh_{\text{t}} + \frac{1}{2}\left( {1 + K_{\text{L}} } \right) \rho_{\text{m}} v_{\text{out,m}}^{2}, $$

(1)

where P_m is the pressure on the metal surface,$\Delta P_{\text{pb,m}}$ is the pressure drop due to particle bed friction, $\Delta P_{\text{t}}$ is the pressure drop due to frictional losses in the tap-hole, P_out is the pressure at the outlet of the tap-hole (P_out = 0), $v_{m}$ is the velocity at the metal surface $\left( {v_{\text{m}} \approx 0} \right)$, $v_{\text{out,m}}$ is the tap-hole outlet velocity of metal, and $\rho_{\text{m}}$ is the metal density. We have also introduced a head loss factor K_L to account for friction losses in the flow converging into the tap-hole (typical value of 0.5 for a sharp transition[15]). Thus, we have

$$ P_{\text{m}} - \Delta P_{\text{pb,m}} - \Delta P_{t} + \rho_{\text{m}} g\left( {h_{\text{m}} - h_{t} } \right) = \frac{1}{2}\left( {1 + K_{\text{L}} } \right) \rho_{\text{m}} v_{\text{out,m}}^{2}. $$

(2)

This expression must be solved to obtain the outlet velocity $v_{\text{out,m}}$ as a function of the other parameters. However, since the pressure drop due to the particle bed and the tap-hole friction are both functions of the outlet velocity, this is not straightforward. The pressure drop through the tap-hole is given by the Darcy–Weisbach expression[15]

$$ \Delta P_{\text{t}} = f\frac{{L_{\text{t}} }}{{2{\text{d}}r_{\text{t}} }}\frac{{L_{\text{t}} }}{{d_{\text{t}} }}\frac{{\rho v_{\text{out}}^{2} }}{2}. $$

(3)

Here, L_t is the length of the tap-hole, r_t is the radius of the tap-hole, and ρ and v_out are the mixture density and velocity in the tap-hole as defined in the mixture-principle applied by Muller et al.[12] The friction factor, f, depends on the Reynolds number of the flow in the tap-hole.[16,17]

The pressure drop due to the particle bed is a function of the local flow velocity through the bed, bed porosity, particle size, and fluid properties. This is often expressed by the Kozeny–Carman equation[13,14] which is valid for laminar flow only or the Ergun equation[18] which covers both laminar and turbulent regimes. These equations need to be integrated over an expected flow path with an expected velocity field. The geometry of the particle bed will affect this integration; for example, particle assemblies under pressure from fluid drag tend to stabilize themselves in certain configurations where effects such as bridging are common.[19] This may result in the formation of an approximately hemispherical cavity adjacent to the tap-hole entrance. It is important to note that bridging may also be complicated by solidified slag and other deposits in the vicinity of the tap-hole causing other stabilizing mechanisms, but these will not be considered here. To check the significance of this effect, two configurations are analyzed as illustrated in Figure 2. Expressions for the pressure drop in each case are shown in Eq. [4] (a full derivation is given in Appendix A).

Fig. 3

Flow field and particle bed configuration close to tap-hole—full bed at right (a), bed with bridging cavity at left (b)

$$ \begin{aligned} &{\text{Ergun from }}r = 0\quad \frac{{150 \mu_{\text{m}} }}{{\varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{t} + \frac{{1.75 \rho_{m} }}{{3 \varPhi d_{p} }}\frac{{\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} }}v_{\text{out,m}}^{2} r_{t} \hfill \\& {\text{Ergun from }}r = r_{\text{t}} \quad \frac{{150 \mu_{\text{m}} }}{{2 \varPhi^{2} d_{p}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{\text{t}} + \frac{{1.75 \rho_{m} }}{{12 \varPhi d_{p} }}\frac{{\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} }}v_{\text{out,m}}^{2} r_{t} \hfill \\ & K - C{\text{ from }}r = 0\quad \frac{{180 \mu_{\text{m}} }}{{\varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{\text{t}} \hfill \\ & K - C{\text{ from }}r = r_{\text{t}} \quad \frac{{180 \mu_{\text{m}} }}{{2 \varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{\text{t}} \hfill \\ \end{aligned}. $$

(4)

Here, μ_m is the fluid viscosity, ε is the particle bed porosity, $d_{\text{p}}$ is the particle diameter, Φ is the particle sphericity, and as before $r_{\text{t}}$ is tap-hole radius. Note that all properties are assumed to be constant along the integration path. This is a simplification which could be explored in future work. We see that a particle bed configuration originating at a sphere one tap-hole radius inside the furnace has less than half of the pressure drop compared to a particle bed extending all the way to the tap-hole.

These expressions can be generalized to

$$ \Delta P_{\text{pb,m}} = A_{{\Delta {\text{P}}}} v_{\text{out,m}} + B_{\Delta P} v_{\text{out,m}}^{2} $$

(5)

which can be inserted in Eq. [2] and rearranged to give

$$ P_{\text{m}} - \Delta P_{\text{t}} - A_{{\Delta {\text{P}}}} v_{\text{out,m}} - B_{\Delta P} v_{\text{out,m}}^{2} + \rho_{\text{m}} g \Delta h_{\text{m}} = \frac{1}{2}\left( {1 + K_{L} } \right)\rho_{\text{m}} v_{\text{out,m}}^{2}. $$

(6)

When solving for the outlet velocity of metal, we get a quadratic equation with the following solution:

$$ v_{\text{out,m}} = \frac{{\sqrt {A_{\Delta P}^{2} + 2\left( {\left( {1 + K_{\text{L}} } \right) \rho_{\text{m}} + 2B_{{\Delta {\text{P}}}} } \right)\left( {P_{\text{m}} - \Delta P_{\text{t}} + \rho_{\text{m}} g \Delta h_{\text{m}} } \right)} - A_{\Delta P} }}{{\left( {1 + K_{\text{L}} } \right) \rho_{\text{m}} + 2B_{\Delta P} }}, $$

(7)

where

$$ \Delta h_{\text{m}} = h_{\text{m}} - h_{\text{t}}. $$

(8)

If the pressure on the metal surface is sufficiently large, it is possible for metal to be tapped even if the metal level is lower than the lowest level of the tap-hole. The pressure on the metal surface is given by the weight of the slag layer, a furnace pressure (e.g., from gas production), and potentially the weight of the particle bed if this floats on the metal surface

$$ P_{\text{m}} = P_{\text{fur}} + P_{\text{pb}} + \rho_{\text{s}} g\left( {h_{\text{s}} - h_{\text{m}} } \right), $$

(9)

where $P_{\text{fur}}$ is the furnace pressure and $P_{\text{pb}}$ is the pressure from the weight of the particle bed. The tapping rate is then given by

$$ \dot{m}_{\text{out,m}} = \rho_{\text{m}} v_{\text{out,m}} A_{\text{out,m}}, $$

(10)

where $A_{\text{out,m}}$ is the cross-sectional area of the tap-hole covered by metal. Note that as metal is drained the volume loss of metal in the furnace and consequently reduction in metal level needs to correct for the presence of the particle bed

$$ \dot{h}_{\text{m}} = \frac{{\dot{m}_{\text{out,m}} }}{{\rho_{\text{m}} \varepsilon A_{\text{f}} }}. $$

(11)

Here, $\varepsilon$ is the particle bed porosity and $A_{\text{f}}$ is the base area of the furnace.

A similar set of equations applies to the slag phase. Note that the driving force at the slag surface does not have any contribution from a liquid phase on top of itself

$$ P_{s} = P_{\text{fur}}. $$

(12)

In order for tapping to occur, $v_{\text{out,m}} > 0$ and/or $v_{\text{out,s}} > 0$. In addition, the slag–metal interface needs to be positioned such that the phases actually cover parts or all of the tap-hole. The position of the interface at the tap-hole is given by a suction deformation,${{\Delta }}z_{\text{st}}$, on the interface

$$ h_{\text{m}} - h_{\text{out}} = {{\Delta }}z_{\text{st}}. $$

(13)

The derivation of an expression for the suction deformation is given in Appendix B where it is also shown that accounting for this effect is significant. By not including this effect, calculations can give erroneous predictions of the time at which metal and slag starts or stops tapping.

Equations [1] through [13] define a reduced order model for furnace drainage during tapping. Bernoulli’s principle describes the flow along a streamline which in principle is a 0D description, as opposed to CFD models of tapping which are typically implemented in two or three spatial dimensions.

Model Validation

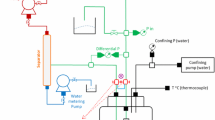
Validation demonstrates how consistent a mathematical or numerical model is when compared to reality in the form of experimental or industrial data. Drainage experiments with multiphase liquids or particle beds are somewhat uncommon; an example is available in Vångö et al.,[20] who performed tests using water and wood chip particles. The experiment was performed in a 400-mm-tall vessel with a footprint of 330 × 150 mm and a water level of 300 mm. Spherical wood chips were used as the granular material for the packed bed. After the wood chips were saturated with water, they achieved an equivalent radius of 6.5 mm and density of 850 kg/m³. The authors do not specify the height to which the vessel was filled with particles, but this was estimated using the total mass of water used (9 kg) and assuming a particle bed porosity between 0.35 and 0.45 which should cover possible packing range for uniformly sized particles.

Comparison between model and experiments were performed with various porosity and correlations for the particle bed pressure drop. Model parameters are equivalent to those in the experiments as given by Vångö et al.[20] No cavity was accounted for in the particle bed close to the tap-hole as this experiment was rigged without a cavity. The comparison is seen in Figure 4—the left figure shows results with the Ergun equation and a range of particle bed porosities typical for random spherical packing.[21] There is reasonable consistency between model results and experimental data in this case. The right-hand figure shows model results for a porosity of 0.35 and particle resistance given by both the Ergun equation and the Kozeny–Carman equation. The comparison with the experimental data clearly shows that the Ergun equation is a much more accurate representation of particle bed flow resistance. This can be explained by a brief analysis of the flow regime in the particle bed. If we calculate a Reynolds number based on the particle size and the outlet velocity, we obtain a value which represents the flow regime in the region very close to the tap-hole entrance. This Reynolds number is higher than that representing the flow in the interior of the vessel further away from the tap-hole. Since most of the pressure drop is created in the converging flow close to the tap-hole, the Reynolds number in this region is the appropriate parameter to use in assessing the nature of the flow. This number exceeds 3000 at the beginning of the tap, indicating that the flow is not laminar, and the Kozeny–Carman equation is not valid.

Fig. 4

Tapped water as function of time from experimental observations and model predictions with different particle porosity (a) and pressure drop correlations (b)

Model Results and Discussion

The reduced order model was used to study the effect of several parameters on the tapping behavior in an example furnace case, as described in Table I.

Table I Parameters for Basic Case

Model Sensitivity to Particle Bed Pressure Drop Expression

The choice of particle bed representation providing a pressure drop through the particle bed during furnace tapping is an important model input. The current model includes four choices for estimating the pressure drop over the particle bed (Eq. [4]). The effect of the different choices is shown in Figure 5, based on the tapping scenario defined by Table I. We see that the choice of representation of the particle bed flow resistance significantly affects the results. The Kozeny–Carman equation gives a lower particle bed resistance and hence higher tapping rates. The quadratic term in the Ergun equation becomes significant in this case since the flow accelerates to appreciable velocities as the liquids are squeezed through the tap-hole. With the above definition of the Reynolds number, we have Reynolds numbers for the metal flow in the range of 20,000 to 40,000 and for slag 200 to 700. This indicates that the flow regime is likely to be turbulent, as metal tapping rates are higher than slag tapping rates. These effects are difficult to capture with the mixture models used by previous authors in which the effective liquid viscosity always contains a contribution from the slag, which is far more viscous than the metal. The mixture model therefore tends to overpredict fluid viscosity, and in turn underpredicts turbulence. For models treating slag and metal as separate phases, turbulence in the flow through the porous bed near to the tap-hole entrance is a significant effect, and the Ergun equation should be applied.

Fig. 5

Evolution of tapping rate (a) and liquid levels (b) during tapping with four models for particle bed pressure drop. Gray horizontal lines indicate top and bottom of tap-hole

There are also significant differences in the results depending on how the particles are arranged close to the tap-hole. This sensitivity is due to the converging and accelerating flow in this region, with the result that much of the bed pressure drop happens here. Although it is not straightforward to assess which configuration is most representative of reality, the main lesson is that tapping rates are sensitive to particle bed configurations in the region where the flow is converging into the tap-hole; more experimental and theoretical study is strongly recommended.

In all following sections, the Ergun equation with no bridging cavity has been selected as the flow physics model.

Model Sensitivity to Bed Particle Size

Another important aspect of the particle bed is the size of the particles, which has a strong effect in the bed pressure drop expression. The sensitivity of the model to this parameter is seen in Figure 6, where particle diameters of 1, 2, and 3 cm are compared against a case with infinite particle size (equivalent to no particle bed being present). Bed particle size is seen to have a significant impact on the tapping flowrates predicted by the model, with larger particles producing a lower bed pressure drop and therefore higher flowrates. This is also seen in earlier work on blast furnaces.[11]

Fig. 6

Evolution of tapping rate (a) and liquid levels (b) during tapping with different particle sizes compared against scenario without particles. Gray horizontal lines indicate top and bottom of tap-hole

Driving Force for Tapping

The weight of the slag and metal above the tap-hole gives rise to a hydrostatic pressure which is the primary driving force in the drainage process. Other phenomena can make additional contributions. For example, gas production from the smelting reactions occurring inside the furnace may create an over-pressure at the upper surface of the slag layer. This can be significant in cases where the rate of gas production is high and the burden has a low permeability. In addition, excavations of manganese ferro-alloy furnaces have shown that no solid particulate matter is found in the metal layer at the bottom of the furnace.[3,5,6] This is often interpreted to mean that the particle bed floats on top of the metal during normal operation of the furnace—in such cases, the bed would be expected to exert an additional pressure on the metal due its own weight. This is somewhat unexpected, since a simple force balance calculation will show that the particle bed should push through the metal layer to the bottom of the furnace as soon as an appreciable burden layer is present. The inconsistency between the dig-out observations and the force balance remains an open research question on submerged-arc furnaces, but the implications of both results can be studied using the reduced order model.

Three simulations with different driving forces were carried out with the base model parameters in Table I. The first simulation used hydrostatic pressure from the liquid levels only, the second liquid levels combined with gas pressure, and the third liquid levels combined with particle bed pressure on metal layer. The gas pressure was set to 0.1 bar and the particle bed pressure exerted by a bed of height 2 m, particle density of 2000 kg/m³, and porosity of 0.4. The results are given in Figure 7, and show that although the additional driving force from gas pressure or particle bed weight increases the tapping rates as expected, the main driving force in this scenario remains the hydrostatic pressure from the liquid levels. The additional tapping forces are significant, but do not dominate the solution.

Fig. 7

Evolution of tapping rate (a) and liquid levels (b) during tapping with different governing mechanisms for the applied pressure during tapping. Gray horizontal lines indicate top and bottom of tap-hole

Conclusion

A reduced order model was derived for simultaneous drainage of two immiscible liquids from a vessel through a single outlet channel in the presence of a porous bed. Such models are applicable to the tapping of slag and metal from smelting furnaces such as those used for ferro-manganese and ferro-silicon production. The model is similar to previously published models in the blast furnace community, but adds functionality to account for the deformation of the slag/metal and slag/gas interface toward the tap-hole and emphasizes on an alternative correlation for the pressure drop in the particle bed. The model was seen to be consistent with both experimental observations of drainage of water from a vessel filled with a particle bed, and CFD simulations of tapping of slag and metal without porous media present.

Results from the model showed that the choice of expression for the particle bed pressure drop has a large impact on the predicted flow rates, with the Ergun equation found to give best performance of the options tested. Earlier work applies the Kozeny–Carman equation which strictly only applies to laminar flow. Analysis also showed that the particle bed configuration close to the tap-hole significantly affects the predicted tapping rates. The flow resistance from the particle bed is significant in most cases, and increases with decreasing particle size.

Much additional work is possible in this area. In particular, both the prediction of the interface deformation due to the suction force and the understanding of particle packing and bridging at the tap-hole entrance can be expanded and improved in future work. Inclusion of additional geometric and physical phenomena affecting flow patterns in the vicinity of the tap-hole can be explored and would improve the generality of such models. Finally, data from two-phase fluid drainage experiments in the presence of porous media would be of great value in order to perform more extensive and comprehensive validation studies.

Appendices

Appendix A: Pressure Drop Through Particle Bed

The pressure drop due to the particle bed is a function of the local flow velocity through the bed. Thus, an expression for the velocity field is required. An analytical expression is not available if there are several liquid phases involved and complex geometrical obstructions are present, but if we assume a radial inflow of a single fluid toward the tap-hole (see also Figure 3), we get

$$ v_{r} = \left\{ \begin{array}{ll} \frac{{v_{\text{out}} }}{2}\left( {\frac{{r_{t} }}{r}} \right)^{2}& \quad r \ge r_{t}, \hfill \\ \frac{{v_{\text{out}} }}{2}&\quad r < r_{t} \hfill \\ \end{array} \right. $$

(A1)

which satisfies the continuity equation in spherical coordinates. This velocity field can be applied when integrating over a flow path to estimate the pressure drop due to resistance in the particle bed. Several expressions for the pressure drop exist. The most common are the Kozeny–Carman equation[13,14]

$$ \frac{{\Delta P_{\text{pb,m}} }}{\Delta r} = \frac{{180 \mu_{\text{m}} }}{{\varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{r}} $$

(A2)

and the Ergun equation[18]

$$ \frac{{\Delta P_{\text{pb,m}} }}{\Delta r} = \frac{{150 \mu_{\text{m}} }}{{\varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{r}} + \frac{{1.75 \rho_{\text{m}} }}{{\varPhi d_{\text{p}} }}\frac{{\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} }}v_{\text{r}}^{2}. $$

(A3)

Using Eq. [A1], these expressions can be integrated from the origin of the particle bed at the tap-hole entrance to a representative distance, R, away from the tap-hole. Two configurations are pursued as illustrated in Figure 3 and discussed in the model section. The pressure drop due to these particle bed configurations is the outcome of the following integration:

$$ \mathop \smallint \limits_{0}^{R} \frac{{\Delta P_{\text{pb,m}} }}{\Delta r} {\text{d}}r\quad {\text{or}}\quad \mathop \smallint \limits_{{r_{t} }}^{R} \frac{{\Delta P_{\text{pb,m}} }}{{\Delta {\text{r}}}} {\text{d}}r. $$

(A4)

The pressure drop is then

$$ \begin{aligned} {\text{Ergun from }}r = 0\quad \frac{{150 \mu_{\text{m}} }}{{d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{\text{t}} \left( {1 - {\raise0.7ex\hbox{${r_{\text{t}} }$} \!\mathord{\left/ {\vphantom {{r_{\text{t}} } {2R}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2R}$}}} \right) + \frac{{1.75 \rho_{\text{m}} }}{{3 \varPhi d_{\text{p}} }}\frac{{\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} }}v_{\text{out,m}}^{2} r_{\text{t}} \left( {1 - {\raise0.7ex\hbox{${r_{\text{t}}^{3} }$} \!\mathord{\left/ {\vphantom {{r_{\text{t}}^{3} } {4R^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${4R^{3} }$}}} \right) \hfill \\ {\text{Ergun from }}r = r_{\text{t}} \quad \frac{{150 \mu_{\text{m}} }}{{d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{\text{t}} \left( {\frac{1}{2} - {\raise0.7ex\hbox{${r_{\text{t}} }$} \!\mathord{\left/ {\vphantom {{r_{\text{t}} } {2R}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2R}$}}} \right) + \frac{{1.75 \rho_{\text{m}} }}{{3 \varPhi d_{\text{p}} }}\frac{{\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} }}v_{\text{out,m}}^{2} r_{\text{t}} \left( {\frac{1}{4} - {\raise0.7ex\hbox{${r_{\text{t}}^{3} }$} \!\mathord{\left/ {\vphantom {{r_{\text{t}}^{3} } {4R^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${4R^{3} }$}}} \right) \hfill \\ K - C{\text{ from }}r = 0\quad \frac{{180 \mu_{\text{m}} }}{{\varPhi^{2} d_{p}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{t} \left( {1 - {\raise0.7ex\hbox{${r_{t} }$} \!\mathord{\left/ {\vphantom {{r_{t} } {2R}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2R}$}}} \right) \hfill \\ K - C{\text{ from }}r = r_{\text{t}} \quad \frac{{180 \mu_{\text{m}} }}{{\varPhi^{2} d_{\text{p}}^{2} }}\frac{{\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} }}v_{\text{out,m}} r_{t} \left( {\frac{1}{2} - {\raise0.7ex\hbox{${r_{\text{t}} }$} \!\mathord{\left/ {\vphantom {{r_{\text{t}} } {2R}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2R}$}}} \right) \hfill \\ \end{aligned}. $$

(A5)

Normally the maximum size of the bed R is much larger than the tap-hole radius $r_{t}$. With little loss of generality, we can therefore assume $R \to \infty$ giving the expressions listed in the model section above.

Appendix B: Interface Deformation Models in Furnace Tapping

If we assume that the interface is above the tap-hole, and far enough away from the tap-hole that it is does not contact the tap-hole even when deformed (see Figure 2), then from Bernoulli’s principle we can calculate the stagnation (suction) pressure $P_{st}$ required to reduce the velocity field in Eq. [A1] to zero at the interface:

$$ P_{{{\text{st}}}} = \frac{1}{2}\rho _{{\text{m}}} v_{{\text{r}}}^{2} = \frac{{\rho _{{\text{m}}} v_{{{\text{out,m}}}}^{2} r_{{\text{t}}}^{4} }}{{8r^{4} }} = \frac{{\rho _{{\text{m}}} v_{{{\text{out,m}}}}^{2} r_{{\text{t}}}^{4} }}{{8\left( {h_{{\text{m}}} - h_{{\text{t}}} - \Delta z_{{{\text{st}}}} } \right)^{4} }}. $$

(B1)

As before, $\rho_{\text{m}}$ is the density of the fluid flowing in the tap-hole (in this case metal), $h_{\text{m}}$ is the undeformed slag–metal interface position relative to the furnace bottom, $h_{\text{t}}$ is the tap-hole centerline position relative to the furnace bottom, and $\Delta z_{\text{st}}$ is the deformation of the interface at the furnace sidewall.

The stagnation pressure can additionally be defined by the change in local hydrostatic pressure due to the deformation of the interface:

$$ P_{\text{st}} = \left( {\rho_{\text{m}} - \rho_{\text{s}} } \right)g\Delta z_{\text{st}}. $$

(B2)

Combining Eqs. [B1] and [B2] gives

$$ \Delta z_{{{\text{st}}}} = \frac{{\rho _{{\text{m}}} v_{{{\text{out,m}}}}^{2} r_{t}^{4} }}{{8g\left( {\rho _{{\text{m}}} - \rho _{{\text{s}}} } \right)\left( {h_{{\text{m}}} - h_{{\text{t}}} - \Delta z_{{{\text{st}}}} } \right)^{4} }}. $$

(B3)

This is a fifth-order polynomial in $\Delta z_{\text{st}}$ and in general cannot be solved analytically; however, it can be used in its implicit form to derive expressions for some important limiting cases.

As the interface drops toward the tap-hole, the stagnation deformation gets larger and larger. At some critical value $h_{m,c}^{ + },$ the deformed interface will touch the top edge of the tap-hole and slag will start entering the channel:

$$ h_{\text{m,c}}^{ + } - h_{\text{t}} - \Delta z_{\text{st}} = r_{\text{t}}. $$

(B4)

Substituting into Eq. [B3] gives

$$ h_{\text{m,c}}^{ + } = h_{\text{t}} + r_{\text{t}} + \frac{{\rho_{\text{m}} v_{\text{out,m}}^{2} }}{{8g\left( {\rho_{\text{m}} - \rho_{\text{s}} } \right)}}. $$

(B5)

A similar development can be performed for the case when the interface is below the tap-hole (i.e., only slag is flowing through the channel and the interface is drawn upward):

$$ h_{\text{m,c}}^{ - } = h_{\text{t}} - r_{\text{t}} - \frac{{\rho_{\text{s}} v_{\text{out,s}}^{2} }}{{8g\left( {\rho_{\text{m}} - \rho_{\text{s}} } \right)}}. $$

(B6)

This gives upper and lower bounds for “pure phase” flow in the tap-hole based on tapping conditions. Note that in these equations the tapping velocity is that of the phase concerned, i.e., metal in Eq. [B5], and slag in Eq. [B6].

It is important to note that the calculation of stagnation interface deformation fails in the case where both phases are flowing simultaneously—this over-simplified approach results in the same upward and downward stagnation pressure at the interface, with the result that no deformation is predicted to occur. This is obviously unrealistic, and may be overcome by simply interpolating between $h_{m,c}^{ - }$ and $h_{m,c}^{ + }$ to estimate the value of $h_{\text{out}}$ (and hence ${{\Delta }}z_{st}$) in cases where $h_{m}$ lies between them. At present, this is the approach implemented in the solution strategy for the reduced order model, although a more rigorous study would be of value here.

Interface Deformation and CFD Benchmark

As noted above, the deformation of the slag–metal interface close to the tap-hole due to the suction force makes it possible for slag to tap earlier than if no interface deformation occurs. The expression derived for this deformation is based on the several simplifying assumptions presented here, and its validity should therefore be checked. As relatively little experimental data for interface deformation during drainage of multiple immiscible liquids from tanks with side-positioned outlets are publicly available, a comparison against CFD simulations was conducted. For multiphase flow, CFD models apply a volume-of-fluids (VOF) method to track multiple fluids and the interface between them, and have been validated in earlier studies related to furnace tapping.[22,23] For a given geometry and with sufficient grid resolution, the results are fairly accurate. A series of transient three-dimensional CFD simulations of a simple geometry consisting of a multiphase flow entering a circular outlet was conducted using the open source computational mechanics code OpenFOAM^®. No particles where accounted for, and the initial metal level was varied from above to below the outlet. All other properties were equal to those in Table I. The CFD simulations were only run for a short time (10 seconds) to establish the interface deformation and initial tapping rates. Simulations with the reduced order model were also calculated using the same parameters. The interface deformation due to the suction force was either accounted for by the expression derived in this appendix or neglected completely in the simulations with the reduced order model. The results of these comparisons are seen in Figure B1.

Fig. B1

Comparing initial tapping rates as function of initial metal level between reduced order model predicting interface deformation, reduced order model neglecting interface deformation, and CFD model

When the initial level of the slag-metal interface is well below the tap-hole channel, no metal is drained. In both the CFD simulations and the reduced order model with deformation, metal starts to drain well before the actual level is above the bottom of the tap-hole, with the deformation being slightly overpredicted by the reduced order model compared to the CFD model. Neglecting the interface deformation in the reduced order model gives significant deviations when compared to the CFD results. The same trend is observed in the slag tapping rates. If one assumes that the CFD results represent reality to an acceptable degree, it is fair to say that interface deformation needs to be accounted for in furnace tapping problems. The presented expression for interface deformation is reasonably accurate considering its simplicity, although further development and testing against experimental data is strongly recommended.