Drainage Model of Multi-taphole Blast Furnaces

Abstract

A drainage model of a multi-taphole hearth of a (large) blast furnace operated by alternate tappings has been developed. The model, which is based on a simplified treatment of the pressure losses in the dead man, taphole entrance and taphole, can estimate the liquid levels and outflow rates of the two liquid phases in quasi-stationary and dynamic states. The sensitivity of the results to changes in the conditions, such as taphole length and diameter, dead-man porosity, as well as in the model parameters is illustrated. The effect of asymmetric conditions at the two tapholes, and dynamic responses of particular interest are also illustrated and discussed. The results of the model are finally compared with findings from a reference blast furnace where the outflows rates of iron and slag are routinely estimated, demonstrating that several of the typical outflow patterns observed in the furnace can be at least quantitatively reproduced. This demonstrates the feasibility of the model as a tool for gaining deeper insight into the complex drainage with alternating tappings and the evolution of the liquid levels in the hearth of large blast furnaces.

Introduction

The blast furnace is the primary unit in the production chain where iron ores are processed to liquid iron before the conversion into steel. The process can be characterized as a huge chemical reaction with simultaneous heat and mass transfer and chemical reactions. The multi-phase flow is extremely complex, and different regions are characterized by the presence of different phases that interact. In the lowest part, the hearth, the main product (molten iron also called hot metal) and the by-product (molten slag) are accumulated with the lighter slag floating on top of the heavier iron. The liquids are tapped intermittently through tapholes that are drilled through the hearth sidewall refractory and closed by a gun injecting taphole clay. The furnace drainage is complex since both liquid phases are drained through the same taphole.[1] In furnaces with large hearth diameter multiple tapholes are used. Large furnaces typically have three or four tapholes, and it is common to use two of them alternately, keeping the remaining one(s) idle. After operating two tapholes a number of weeks one or both of them may be replaced and another taphole pair starts tapping. Since the conditions inside the hearth are harsh, with aggressive molten phase at high temperature, it is not possible to measure the internal state. Thus, e.g., the internal levels of the liquids are unknown. The conditions are further complicated by the fact that the liquids in the hearth only occupy the void between a coke bed that extends (close) to the hearth bottom. This coke bed, called dead man, has largely unknown properties, and the way in which it affects the internal liquid flows is not obvious. In particular, the conditions in front of the drilled taphole are important, because the liquids accelerate on their way towards the taphole, which means that the main internal pressure drop occurs relatively close to the entrance of the taphole. Due to the above reasons, the blast furnace tapping process is challenging and a lack of deep understanding of the phenomena still limits the success of controlling the draining process.[2]

The outflow patterns are known to be complicated. The flow, which is mainly induced by the gas pressure in the furnace, experiences viscous and inertial losses both in the dead man and in the taphole, where the latter contributes by the major part. However, as the more viscous slag flows out, a considerable pressure drop occurs already in the coke bed, lowering the static pressure in the immediate vicinity of the taphole. This makes it possible to drain iron to levels well below the taphole during the simultaneous outflow of both phases, and also to lift iron from levels below the taphole even in taps that start with slag-only outflow.[3] The viscous losses in the slag also lead to a declivity of the slag-gas interface towards the taphole, and as a result considerable quantities of slag may remain in the hearth after the tapping ends: the taphole is usually plugged after gas starts bursting out. These matters complicate the dynamics of the liquids in the hearth. In addition, large furnaces may show spatial variation in the liquid levels caused by differences in the dead-man porosity, e.g., impermeable regions caused by coke degradation, accumulation of coke fines or insufficient carburization rate of the hot metal.[4]

Due to the complexity of the hearth drainage, several investigators have tackled the problem by small-scale experiments or mathematical modeling. The fact that the iron-slag interface may descend well below the taphole was first pointed out and demonstrated in laboratory scale in Australia by Tanzil and co-workers.[3] The findings partly revised the earlier results on slag drainage presented by Fukutake and Okabe.[5,6] The work in Australia was continued by Zulli,[7] who refined the expressions of the residual slag by considering the motion of both interfaces. These findings were used in a model by Nightingale et al. for estimating the coke-bed voidage in operating blast furnaces.[8] Opberger and Toxopeus[9] developed a simplified hearth drainage model inspired by findings in industrial furnaces, assuming a full mixing of the two phases in the taphole, using average liquid properties to estimate the pressure drop. The authors reported outflow patterns in general agreement with observations from a large blast furnace. Based on the main findings of Nightingale et al.,[8] Brännbacka et al.[10] developed a simplified model for simulation of hearth drainage in small (one-taphole) blast furnaces, considering a possible motion of the dead man caused by the buoyancy forces of the hearth liquids. This conceptual model was shown to be able to estimate whether the dead man sits or floats in operating blast furnaces.[11,12] Shao and Saxén[13] later extended the model to consider the pressure drop in the slag by integrating the Kozeny-Carman equation in front of the taphole, and the pressure drop in the taphole using a model based on fully stratified flow of iron and slag. The authors demonstrated how the model could be used to select drill-bit diameter to achieve a given (aim) duration of the taps in a simulated one-taphole furnace.

Nouchi et al.[14] studied hearth drainage experimentally in the laboratory with a three-dimensional model and clarified cases where the dead-man floating level was high and or the central part of the dead man was clogged. The simplified drainage model developed in the work was later applied by Iida et al.,[15,16] who, like earlier investigators,[9] considered iron and slag to be fully mixed in the taphole. The pressure loss in front of the taphole was determined by a one-dimensional flow model through a “porous plug”, the length of which was adapted to yield outflow rates in agreement with observations in large Japanese blast furnaces. A multi-pool model was applied to consider spatial differences in the liquid levels and the authors studied the effect of impermeable zones. They hypothesized that a division of the hearth into two or three pools of different permeability could explain the observed drainage imbalance in the reference furnaces. Saxén[17] developed a similar quasi-stationary two-pool hearth model representing the regions around the operating tapholes and studied how the cross-pool flows and dead-man floating would affect the liquid levels. In this model, the inter-cast period was taken to be sufficiently long to justify the assumption of iron-only flow in the beginning of the taps and the outflow rates of iron and slag were fixed based on the production rates to satisfy the material balances. Roche et al.[18] developed a two-zone model with variable pool size and studied the effect of various variables and asymmetry on the liquid levels. The outflow patterns were pre-set based on observations from a reference blast furnace.

Mathematical models based on a more detailed description of the fluid flows have also been reported. Nishioka et al.[19] studied the liquid levels and flow patterns in quasi-stationary state by a three-dimensional CFD model considering the taphole as a pipe (of growing diameter due to taphole erosion) with mixed flow of iron and slag. The shares of iron and slag in the taphole were taken to be equal to the corresponding shares in the computational cell next to the taphole entrance in the hearth. To the best of the present authors’ knowledge, the model by Nishioka et al. is the only rigorous CFD model in the literature by which the conditions during consecutive taps of iron and slag have been simulated. Obvious challenges in the CFD modeling are the different length scales of the system and the simultaneous drainage of two liquid phases, as well to properly describe the conditions in the porous bed in front of the taphole. Recently, attempts have been made to understand the operation of the hearth by considering not only fluids but also the motion of coke by a combination of CFD and the Discrete Element method (DEM). Bambauer et al.[20] simulated the whole (but down-scaled) blast furnace by CFD-DEM, including the hearth with one liquid phase, and demonstrated how the liquid levels and dead-man coke evolved along the tap cycle. Vångö et al.[21] studied single drainage patterns of a three-dimensional hearth with iron and slag, where the coke particles were allowed to move along with liquid flow and buoyancy.

In summary, considerable efforts have been spent in clarifying the changes of the liquid levels in and outflows of iron and slag from the blast furnace hearth, both with pilot models and numerical methods of different degrees of sophistication. However, the models’ results have only been compared to single measured outflow patterns and little work has been reported on model-based analysis of the different drainage patterns that are observed in real blast furnaces.[22,23] The computational requirement of CFD models still seems prohibitive for using this technique to mimic the drainage patterns observed in the real operation, considering the fact that several tap cycles have to be simulated until a quasi-stationary state is reached. Furthermore, it is also of interest to study dynamic responses, e.g., at disturbances or when the internal hearth conditions gradually change. Even though some studies have considered the flow in the taphole in a more realistic way, the large differences in the flowrates in the hearth and taphole call for a large number of computational cells, and the description of the interfaces is particularly problematic and susceptible to numerical problems.

These challenges inspired the present investigators to develop a fast model that still considers most of the important features of the problem at hand, for simulating the liquid levels and outflows for a hearth with two operating tapholes. Section II of the paper presents the assumptions made in the modeling and the main equations. Section III illustrates some results of the model under different conditions. In Section III–A, the conditions at the two alternating tapholes are assumed to be identical, while they are different in the results of the following subsection. Section III–C briefly studies dynamic behavior. An interesting comparison of the drainage patterns of a large blast furnace and the outflows predicted by the model is provided in Section IV, demonstrating the feasibility of the model. Finally, some concluding remarks and lines of future development are provided in Section V.

Model

Background

In large blast furnaces with multiple tapholes, the outflows may show different types of patterns and also individual differences may occur or disappear suddenly or gradually.[22] A reason for this is that for a hearth operated with a short inter-cast period, the iron-slag interface may not have time to rise above the other taphole before it is opened, yielding slag-first taps (showing “negative slag delays”, $t_{\text{sd}} < 0$). Conversely, if the iron-slag level does not descend low enough before the tap ends, the next tap may start with simultaneous outflow of iron and slag, or even with iron-first flow (i.e., “positive slag delay”, $t_{\text{sd}} > 0$) which is characteristic of single-taphole BFs. The order in which the phases are drained out is likely to play a role for the tapping rates, since the pressure and local conditions at the taphole inlet are affected by the liquid levels. The model outlined in the following sections tackles this problem in a simplified way using basic fluid mechanics.

Main Assumptions

The mathematical model is based on the following main assumptions:

• 1. The volumes of iron and slag in the hearth are characterized by overall levels, $z_{\text{ir}}$ and $z_{\text{sl}}$

• 2. For every time moment, the outflows are taken to be in a quasi-stationary state.

• 3. The hearth diameter ($d_{\text{h}}$) and the voidage ($\varepsilon_{\text{h}}$) of the dead man are given and the dead man is assumed to sit on the hearth bottom.

• 4. The inflow rate of iron to the hearth, $\dot{m}_{{{\text{ir}},{\text{in}}}}$, and the slag (mass) ratio, $\gamma_{\text{in}}$, are given.

• 5. The taphole diameter ($d_{\text{th}}$), length ($l_{\text{th}}$), angle of inclination ($\alpha_{\text{th}}$) and erosion rate ($e_{\text{th}}$) are given for each taphole.

• 6. Two tapholes are alternated with an inter-cast time, $t_{\text{pl}}$, during which both tapholes are closed.

• 7. Simple conditions are applied to determine the phases that initially flow out when the taphole is opened.

• 8. The tapping ends when the gas-slag interface locally bends down to the taphole.

Basic Equations

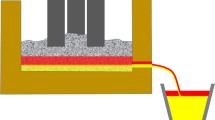
The model tracks the dynamic changes of the iron and slag levels in the hearth by describing the outflow rate of the two phase, considering the conditions in front of and in the taphole. Figure 1 illustrates the BF hearth and the main variables and parameters of the model.

Fig. 1

(a) BF hearth and its main variables and parameters in the model and (b) top view illustrating region for integration of bed pressure loss

Iron and slag enter the hearth at given mass flow rates. The liquid levels in the hearth are expressed as the vertical distance from the inner end of the taphole, which thus acts as the reference point ($z = 0$). The rate of changes in the liquid levels are expressed by differential mass balance equations, written as

$$ \frac{{{\text{d}}z_{\text{ir}} }}{{{\text{d}}t}} = \frac{{\dot{m}_{{{\text{ir}},{\text{in}}}} - \dot{m}_{{{\text{ir}},{\text{out}}}} }}{{\rho_{\text{ir}} A_{\text{h}} \varepsilon_{\text{h}} }}, $$

(1)

$$ \frac{{{\text{d}}z_{\text{sl}} }}{{{\text{d}}t}} = \frac{{{\text{d}}z_{\text{ir}} }}{{{\text{d}}t}} + \frac{{\gamma_{\text{in}} \dot{m}_{{{\text{ir}},{\text{in}}}} - \dot{m}_{{{\text{sl}},{\text{out}}}} }}{{\rho_{\text{sl}} A_{\text{h}} \varepsilon_{\text{h}} }}, $$

(2)

where $\rho_{\text{ir}}$ and $\rho_{\text{sl}}$ are the iron and slag densities, and $A_{\text{h}} = \pi d_{\text{h}}^{2} /4$ is the cross-section area of the hearth.

The mass outflow terms, $\dot{m}_{{{\text{in}},{\text{out}}}}$ and $\dot{m}_{{{\text{sl}},{\text{out}}}}$, in Eqs. [1] and [2] are expressed through pressure balances for the two liquids between the hearth and the surrounding casthouse. These balances are split into two parts, expressing the conditions in the hearth and in the taphole.

$$ p_{\text{g}} = p_{\text{th}} - g\rho_{\text{sl}} z_{\text{sl}} + \Delta p_{{{\text{bed}},{\text{sl}}}} + \Delta p_{{{\text{ent}},{\text{sl}}}} , $$

(3)

$$ p_{\text{g}} + g\rho_{\text{sl}} \left( {z_{\text{sl}} - z_{\text{ir}} } \right) = p_{\text{th}} - g\rho_{\text{ir}} z_{\text{ir}} + \Delta p_{{{\text{bed}},{\text{ir}}}} + \Delta p_{{{\text{ent}},{\text{ir}}}} , $$

(4)

$$ p_{\text{th}} = p_{0} - g\rho_{j} l_{\text{th}} \sin \alpha_{\text{th}} + \Delta p_{{{\text{th}},j}} ; \quad j = {\text{ir}}, {\text{sl}},{\text{mix}} . $$

(5)

In Eqs. [3] and [4], the left-hand-sides express the pressure at the slag-gas and iron-slag interfaces far from the taphole, $p_{\text{th}}$ is the pressure at the entrance of the taphole, $p_{0}$ is the atmospheric pressure, while $\Delta p_{{{\text{bed}},j}}$ and $\Delta p_{{{\text{ent}},j}}$are the pressure losses in the dead man and at the entrance of the taphole for phase $j$ (${ = }\;{\text{sl}}, {\text{ir}}$). The pressure balance over the taphole, Eq. [5], applies to the cases where only iron, only slag, or a mixture of both flows out simultaneously; $\Delta p_{{{\text{th}},j}}$ expresses the pressure loss in the taphole. Figure 1(a) shows a hearth state where both phases are tapped simultaneously.

The pressure drop of the liquids in the dead man is obtained from the Ergun equation[24]

$$ \frac{{{\text{d}}p}}{{{\text{d}}x}} = 150\frac{{\mu_{j} \left( {1 - \varepsilon } \right)^{2} }}{{\left( {d_{\text{c}} \Phi } \right)^{2} \varepsilon^{3} }}u_{j} + 1.75\frac{{\rho_{j} \left( {1 - \varepsilon } \right)}}{{\left( {d_{\text{c}} \Phi } \right)\varepsilon^{3} }}u_{j}^{2} ;\quad j = {\text{ir}},{\text{sl,}} $$

(6)

where $\mu_{j}$ and $u_{j}$ are the viscosity and velocity of phase j, $d_{\text{c}}$ and $\Phi$ are the diameter and shape factor of dead-man coke, and $\varepsilon$ is the voidage of the coke bed in front of the taphole. This equation was applied to the system depicted in Figure 1(b), using $r$ as the spatial coordinate. The cross-section area for the flow is that of a hemisphere, giving the local average velocity $u_{j} = \dot{V}_{j} /\left( {2\pi r^{2} } \right)$, where $\dot{V}_{j} \left( { = \dot{m}_{j} /\rho_{j} } \right)$ is the volume flow rate of phase $j$. Integrating Eq. [6] from the hearth radius ($r_{\text{h}}$) to a minimum radius ($r_{ \hbox{min} }$)

$$ \mathop \smallint \limits_{{r_{\text{h}} }}^{{r_{ \hbox{min} } }} \left( {150\frac{{\mu_{j} \left( {1 - \varepsilon } \right)^{2} }}{{\left( {d_{\text{c}} \Phi } \right)^{2} \varepsilon^{3} }}u_{j} + 1.75\frac{{\rho_{j} \left( {1 - \varepsilon } \right)}}{{\left( {d_{\text{c}} \Phi } \right)\varepsilon^{3} }}u_{j}^{2} } \right){\text{d}}t;\quad j = {\text{ir}},{\text{sl,}} $$

(7)

yields for the pressure loss

$$ {{\Delta }}p_{{{\text{bed}},j}} = 150\frac{{\mu_{j} \left( {1 - \varepsilon } \right)^{2} }}{{2\pi \left( {d_{\text{c}} \Phi } \right)^{2} \varepsilon^{3} }}\left( {\frac{1}{{r_{ \hbox{min} } }} - \frac{1}{{r_{\text{h}} }}} \right)\dot{V}_{j} + 1.75\frac{{\rho_{j} \left( {1 - \varepsilon } \right)}}{{12\pi^{2} \left( {d_{\text{c}} \Phi } \right)\varepsilon^{3} }}\left( {\frac{1}{{r_{ \hbox{min} }^{3} }} - \frac{1}{{r_{\text{h}}^{3} }}} \right)\dot{V}_{j}^{2} ;\quad j = {\text{ir}},{\text{sl}} . $$

(8)

Since the taphole diameter in the blast furnace is not much larger than the (coke) particles of the bed, it is unreasonable to assume that a porous bed of uniform properties extends to the taphole, as this would give and excessive pressure drop as the flow converges. Therefore, the integration limit $r_{ \hbox{min} }$ was set clearly off the taphole entrance (cf. Figure 1(b)); it can be seen as a model parameter, or physically as a taphole “entrance void”, by which different degrees of contact of the coke bed with the taphole can be considered.

In the case where only one phase (iron or slag) flows out, the entrance loss in Eq. [3] can be written as

$$ {{\Delta }}p_{{{\text{ent}},j}}^{\left( 1 \right)} = k_{\text{ent}} \frac{{\rho_{j} }}{2}u_{{{\text{th}},j}}^{2} , $$

(9)

where $k_{\text{ent}}$ is an entrance loss factor and $u_{{{\text{th}},j}}$ is the velocity in the taphole. However, the case with simultaneous outflow of iron and slag, and particularly the one where the iron-slag interface is clearly below the taphole, requires further consideration because the flow of iron is constrained by the slag phase. With reference to Figure 2(a), it is clear that the entrance resistance to iron flow grows as iron is drained deeper below the taphole. To consider the effect of the converging region, another entrance-loss term was introduced

$$ {{\Delta }}p_{{{\text{ent}},{\text{ir}}}}^{\left( 2 \right)} = k_{\text{up}} \frac{{\rho_{\text{ir}} }}{2}\left( {\frac{{\dot{V}_{\text{ir}} }}{{A_{\text{up}} }}} \right)^{2} = k_{\text{up}} \frac{{\rho_{\text{ir}} }}{2}u_{\text{up}}^{2} ; \quad z_{\text{ir}} \le 2d_{\text{th}} . $$

(10)

Fig. 2

Definition of the geometry for estimating the entrance loss for iron for the case where the overall iron level is below the taphole: (a) vertical cross-section and (b) horizontal cross-section

The velocity of the iron phase ($u_{\text{up}}$) is obtained by dividing the volume flow rate by a cross-section area, ($A_{\text{up}}$) at a vertical level two-taphole a certain distance ($2d_{\text{th}}$) below the taphole, as indicated in Figure 2. Close to the taphole the iron-slag interface was assumed to fall on a quarter of a circle with a radius equal to the distance between the taphole and the overall iron-slag interface. This defines the radius, $r_{\text{up}}$, of the semi-circular region with the cross-section area $A_{\text{up}} = \pi r_{\text{up}}^{2} /2$.

A similar procedure was applied to the case where slag is drained together with iron even though the overall iron level is above the taphole.[3,14,25] For this, a corresponding entrance-loss term is

$$ {{\Delta }}p_{{{\text{ent}},{\text{sl}}}}^{\left( 2 \right)} = k_{\text{down}} \frac{{\rho_{\text{sl}} }}{2}\left( {\frac{{\dot{V}_{\text{sl}} }}{{A_{\text{down}} }}} \right)^{2} = k_{\text{down}} \frac{{\rho_{\text{sl}} }}{2}u_{\text{down}}^{2} ;\quad z_{\text{ir}} \ge 2d_{\text{th}} . $$

(11)

Finally, the overall entrance loss in Eqs. [3] and [4] is given by

$$ {{\Delta }}p_{{{\text{ent}},j}} = { \hbox{max} }\left( {{{\Delta }}p_{{{\text{ent}},j}}^{\left( 1 \right)} ,{{\Delta }}p_{{{\text{ent}},j}}^{\left( 2 \right)} } \right). $$

(12)

Finally, the pressure loss in the taphole was taken to be that in a rough pipe, defined as

$$ \Delta p_{{{\text{th}},j}} = f_{j} \frac{{l_{\text{th}} }}{{d_{\text{th}} }}\frac{{\rho_{j} }}{2}u_{{{\text{th}},j}}^{2} ; i = {\text{ir}},{\text{sl}},{\text{mix}} $$

(13)

where $f_{j}$ is the friction factor. This factor is given by Eq. [14a] for laminar flow and by the Colebrook-White equation[26] of Eq. [14b] for turbulent flow

$$ f_{j} = \frac{64}{{{\text{Re}}_{j} }};\;{\text{Re}}_{j} \le 2300, $$

(14a)

$$ \frac{1}{{\sqrt {f_{j} } }} = - 2\log \left( {\frac{2.51}{{{\text{Re}}_{j} \sqrt {f_{j} } }} + \frac{\xi }{{3.7d_{\text{th}} }}} \right);\;{\text{Re}}_{j} > 2300. $$

(14b)

In Eq. [14b], $\xi$ is the roughness of the taphole, and the Reynolds number is given by

$$ {\text{Re}}_{j} = \frac{{u_{{{\text{th}},j}} \rho_{j} d_{\text{th}} }}{{\mu_{j} }}; \quad j = {\text{ir}},{\text{sl}},{\text{mix}} . $$

(15)

The velocity $u_{{{\text{th}},j}}$ was calculated based on the corresponding volumetric flow and the taphole cross-section area. For the case where iron and slag flow out simultaneously, $\rho_{\text{mix}}$ and $\mu_{\text{mix}}$ were obtained as mean values based on the volumetric shares of the two phases. Even though it may be argued that the two phases are not mixed but stratified[13,27] or that they show even more complex flow patterns,[28] this assumption was justified its computational simplicity and as the same approach has been made by other investigators in the field.[9,15,19] The taphole diameter is obtained by integrating

$$ \frac{{{\text{d}}d_{\text{th}} }}{{{\text{d}}t}} = e_{\text{th}} , $$

(16)

using $d_{\text{th}} = d_{{{\text{th}},{\text{ini}}}}$ as the initial condition when the taphole is opened.

Outflow Cases and Tap-End Conditions

After a period when the tapholes have been plugged, and a taphole is opened, the vertical level of the iron-slag interface $z_{\text{ir}}$ was used to determine the initial phase(s) to flow out by the simple condition that only iron flows out if $z_{\text{ir}} \ge z_{\text{th}} - d_{\text{th}} /2$, only slag if $z_{\text{ir}} < - \Delta z_{\text{mix}}$ and otherwise both iron and slag. Obviously, this condition is strongly simplified, so a possible revision of it is undertaken in the next time step based on the previous solution. In case of iron-only flow, an ansatz is made that also slag starts flowing out at a volume flow rate given as a share, $\beta$, of the production rate (i.e., $\dot{V}_{\text{sl}} = {{\beta \dot{m}_{{{\text{sl}},{\text{in}}}} } \mathord{\left/ {\vphantom {{\beta \dot{m}_{{{\text{sl}},{\text{in}}}} } {\rho_{\text{sl}} }}} \right. \kern-0pt} {\rho_{\text{sl}} }}$) and the pressure balance of the slag phase in the hearth (Eq. [3]) is solved with respect to $p_{\text{th}}$. If the value is higher than the taphole pressure determined in the previous solution, simultaneous outflow of iron and slag is assumed to occur. Likewise, in case of an initial slag-only flow, the ansatz is that also iron starts flowing out at a volume flow rate given by $\dot{V}_{\text{ir}} = {{\beta \dot{m}_{{{\text{ir}},{\text{in}}}} } \mathord{\left/ {\vphantom {{\beta \dot{m}_{{{\text{ir}},{\text{in}}}} } {\rho_{\text{ir}} }}} \right. \kern-0pt} {\rho_{\text{ir}} }}$, and the pressure balance of the iron phase (Eq. [4]) is solved with respect to $p_{\text{th}}$. If the value is higher than the taphole pressure of the previous solution, simultaneous outflow of iron and slag is assumed to occur.

In the model the tap end is defined as the time when the gas-slag interface can locally bend down to the taphole. This requires that the pressure loss of slag in the bed and at the taphole entrance balances the head of the slag layer, i.e.,

$$ \Delta p_{{{\text{bed}},{\text{sl}}}} + \Delta p_{{{\text{ent}},{\text{sl}}}} \ge \rho_{\text{sl}} gz_{\text{sl}} . $$

(17)

When this conditions is satisfied, the taphole is plugged and kept close for a time period of $t_{\text{pl}}$, after which the taphole is changed and the procedure is repeated. It should be noted that a transition from two-phase to one-phase flow was banned in the model, since such changes were rarely observed in the reference furnace and could give rise to fluctuating solutions in the model.

Numerical Aspects

The model was implemented in Matlab. The differential Eqs. [1] and [2] were discretized and solved by an explicit scheme using a time step of one minute. The nonlinear algebraic Eqs. [3] through [5] combined with Eqs. [8] through [15] were solved numerically with respect to the two unknowns ($p_{\text{th}} ,\dot{V}_{\text{sl}}$) for time steps of slag-only flow, ($p_{\text{th}} ,\dot{V}_{\text{ir}}$) for iron-only flow, and to the three unknowns ($p_{\text{th}} ,\dot{V}_{\text{sl}} ,\dot{V}_{\text{ir}}$) for time steps where both liquids were tapped. Non-negativity of the unknowns was imposed by applying variable transformations. After setting the geometry and model parameters as well as the initial and boundary conditions, the system was run until a quasi-stationary state was reached. This usually occurred within 5 tap cycles, depending on the initial liquid levels and parameter settings. In some cases the dynamic response to a change was of interest, and then the change was introduced after a quasi-stationary state had been reached. A typical simulation time for a 2500-minute case (comprising about 15 tap cycles) is one minute on a standard laptop.

Results

The model described in Section II was applied to study the evolution of the liquid levels and the outflow rates under different conditions. The sensitivity of the model to its parameters was also studied to gain an understanding of the primary factors that affected the state of the hearth. The simulation results of this section are complemented by practical findings reported in Section IV.

In the present study, the model was applied to study the hearth of a large blast furnace, where two tapholes are alternately used with a short inter-cast period. The base-case conditions and parameter settings are provided in Table I. The geometric parameters (hearth diameter, taphole length and diameter), production rate, slag ratio and blast pressure were estimated from typical values of large blast furnaces (partly from Roche et al.[18]), and the material properties (iron and slag densities and viscosities, taphole roughness, coke particle size and shape factor, as well as bed voidage) from values used in similar numerical studies of the blast furnace hearth in the literature. The time the taphole was plugged was taken to be 6 minutes, which represents a typical “fast” switching between tapholes.[18] The entrance loss factor was set low due to the assumed void at the taphole entrance, while the values used for the additional loss factors ($k_{\text{up}} , k_{\text{down}}$) were set by trial and error to yield reasonable transitions between the two entrance-loss equations in Eq. [12]. As there are practically no means of directly quantifying the progress of erosion of the taphole, most investigators have simply assumed values that give rise to calculated outflows in agreement with observed tapped quantities.[9,15,19] The value used in the present study ($e_{\text{th}} = 3.3 \times 10^{ - 6} {\text{m}}/{\text{s}}$) is somewhat higher than that used by other investigators.

Table I Conditions and Model Parameters for the Base Case

The results to be reported include the evolution of the overall levels of iron and slag in the hearth, the outflow rates, normalized by dividing them by the inflow rates, the duration of the tap, $t_{\text{tap}}$, the slag delay, $t_{\text{sd}}$, as well as the mass ratio of slag in the outflow, $\gamma_{\text{out}}$. For the purpose of illustration, the results for every second tap, referred to as taps from taphole 2 (TH2), have been depicted by dotted lines. In all the graphs, the results for iron and slag are denoted by red and blue lines, respectively, while for the inter-cast period a black line is used. In the dynamic examples, the outflows are not normalized as the inflows (may) vary.

Key drainage indices of the cases are collected in Table II. It must be stressed that taps with slag delays close to zero, $\left| {t_{\text{sd}} } \right| = 1$, in practice would be equivalent to taps where the two liquids appear simultaneously in the runner because these values may arise merely due to the procedure applied in Section II–D to select the initial phase(s) to drain.

Table II Perturbed Terms and Key Drainage Indices for the Examples Presented in Figs. 3 Through 10

Identical Conditions at the Tapholes

In the first part of the study, identical conditions were imposed on the two tapholes and their vicinities, so the resulting tap cycles (liquid levels and outflow rates) should be identical. The first example is the Base case, which simulates the drainage using the conditions and parameter settings of Table I. Figure 3(a) illustrates the resulting slag and iron levels (blue and red lines in the top panel) and the normalized outflow rates (same colors, bottom panel) for a period of 450 minutes of quasi-stationary operation. The outflows were thus normalized by dividing them by the inflows, which means that for values less than one the phase in question is accumulated while for values above one it is depleted. The slag level is seen to be 2-3 m above the taphole while the iron level varies above and below the taphole, yielding a tapping time of $t_{\text{tap}} = 156\;{\text{minutes}}$ and no slag delay; the two liquids start flowing out simultaneously (cf. Table II). The bottom panel shows an interesting outflow behavior: the iron outflow gradually increases but levels out later in the tapping. By contrast, the slag outflow is moderate initially, then decreases to a minimum about 25 minutes into the tap, followed by an almost linear increase, reaching a final level of about twice the production rate. Similar patterns were reported by Nouchi et al.[14] in their small-scale drainage experiments using fluoride (as “iron”) and paraffin (as “slag”), by simplified drainage models,[9,16] by CFD models considering both iron and slag flow,[19] as well as in measurements from operating multi-taphole furnaces.[16,19]

Fig. 3

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) Base case, (b) increased ($\mu_{\text{sl}} = 0.50\; {\text{Pa}}\;{\text{s}}$) and (c) decreased ($\mu_{\text{sl}} = 0.20\; {\text{Pa}}\;{\text{s}}$) slag viscosity. i = ir (red), i = sl (blue) (Color figure online)

The effect of slag viscosity on the results is studied by changing it by $\pm \;0.15 \;{\text{Pa}}\;{\text{s}}$ from the base-case value, Figures 3(b) and (c) show the result of an increase and a decrease of viscosity, respectively. The increased slag viscosity lowers the iron level but raises the slag level, while the opposite holds true for a decrease in slag viscosity. This is due to the fact that the pressure at the taphole decreases with the slag viscosity, which makes it possible to drain iron from lower levels, but simultaneously the end level of the slag is raised (cf. Eq. [17]). In the former case, slag is the first phase to flow out, but the iron is only marginally delayed. The effect on the tap duration is minor due to the shifting of the two interfaces in opposite directions. However, the effect on the outflow patters is considerable: the higher slag viscosity increases the share of slag in the initial part of the tap while a lower viscosity decreases the share. In the latter case, the slow initial outflow rate is due to the high iron-slag interface level, but the lower flow resistance leads to a strong slag flow in the later parts of the tap. This demonstrates the complex effect of the internal conditions on the liquid outflows, where the flow resistance in the coke bed, at the taphole entrance and in the taphole interplay. An interesting detail worth noting is that the case with low slag viscosity shows a short period of iron-only flow in the very beginning of the tap, but the outflow rate is only marginally higher than it is when the slag outflow has started. Thus, the additional slag flow does not substantially affect the pressure drop in the taphole. The fact that the iron outflow rate only slightly dropped as slag enters the taphole was observed also in one-taphole blast furnaces.[29]

The effect on the production rate is studied in Figure 4, which shows the impact of an increase in the hot metal production rate from 11,000 t/day to 12500 t/day (Figure 4(a)) and an increase in the slag ratio from 0.2 to 0.25 (Figure 4(b)). The increase in the production rate leads to longer tapping time (increasing by 27 minutes from the Base case), larger amplitudes of the liquid levels, and a higher slag level. The liquid outflow patterns are very similar to those of the Base case. An increase in the slag ratio by 50 kg per ton of hot metal raises the maximum slag level by almost 0.5 m but conversely lowers the iron level, as the share of slag in the outflow must increase (to close the material balances). The tapping time increases by 13 minutes, but iron and slag still start flowing practically at the same moment.

Fig. 4

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) increased overall production rate ($\dot{m}_{{{\text{ir}},{\text{in}}}} = 12 ,500 \;{\text{t}}/{\text{day}}$) or (b) increased slag ratio ($\gamma_{\text{in}} = 0.25$). i = ir (red), i = sl (blue) (Color figure online)

In the practical operation of the blast furnace, the taphole length varies and mainly depends on the local flow conditions in the hearth and the quality of the taphole clay. The length can be affected by the volume of the injected taphole clay, but it is not always possible to extend the taphole since the formation of the “mushroom” at its inner end requires a good contact between the clay and the coke bed.[30] A strong peripheral flow of the liquids in the hearth, which may be the result of a clogged core of the dead man, is known to lead to a shorter taphole. The effect was investigated by changing the length by ± 1 m from the base-case value: these would represent extreme values encountered in the practical operation. Figure 5(a) demonstrates that the increase, as expected, prolongs the tap considerably (by almost 40 minutes) and therefore also yields larger amplitudes of the liquid levels. The longer taphole also shifts the inner end of the taphole downward, which lowers the liquid levels (with respect to the furnace bottom). The slag level rises somewhat, but the change is not dramatic. The outflow patters largely remain as in the Base case, but the minimum exhibited by the slag outflow is more pronounced. For the short taphole (Figure 5(b)) the tap duration decreases by 50 minutes, which brings down the liquid-level amplitudes and the overall slag level. Along with this change, the share of iron flowing out during the initial part of the tap is increased. For both cases, the tap starts with practically simultaneous flow of iron and slag.

Fig. 5

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) longer ($l_{\text{th}} = 4\; {\text{m}}$) or (b) shorter ($l_{\text{th}} = 2 \;{\text{m}}$) taphole. The inner ends of the two tapholes appear on different levels due to the taphole length difference. i = ir (red), i = sl (blue) (Color figure online)

One of the few variables that can be used to directly affect the drainage is the taphole drill diameter. The effect of the initial taphole diameter is illustrated in Figure 6, which shows the simulated drainage using drill diameters with ± 4 mm offset from the base-case value. The decreased diameter (Figure 6(a)) naturally prolongs the tap (here by more than 40 minutes) and yields higher slag levels in the hearth. The initial outflow rate of iron is somewhat lower and the rate of slag is higher than in the Base case, and the outflow patters are strikingly similar to those for the case with a long taphole (cf. Figure 5(a)). Conversely, an increased diameter (Figure 6(b)) lowers the slag level and raises the iron level in the hearth, which increases the iron flow in the beginning of the tap. The slag outflow rate no longer shows a minimum but increases monotonously. The primary effect of the larger taphole diameter is that the tap duration decreases (Table II).

Fig. 6

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) smaller ($d_{{{\text{th}},{\text{ini}}}} = 0.058 \;{\text{m}}$) or (b) larger ($d_{{{\text{th}},{\text{ini}}}} = 0.070\; {\text{m}}$) initial taphole diameter. i = ir (red), i = sl (blue) (Color figure online)

Closely related to the above is the role of taphole erosion. After increasing or decreasing the rate from the base-case value the main effect was found to be only on the duration of the taps, while the outflow patterns remained practically unchanged.

The voidage of the dead man plays an important role for the liquid levels; a lower voidage means larger changes in the liquid levels as there is less space for the liquids in the bed. The voidage also affects the pressure drop in the bed, particularly close to the tapholes. The effect of voidage is seen in Figure 7, which shows the results for the cases where the overall voidage $\varepsilon_{\text{h}}$ was changed by ± 0.04 from the base-case value. The same change was implemented in the local voidage ($\varepsilon$) in front of the tapholes. Such changes could be due to changes in coke quality, or in the residence time of coke in the upper furnace. The outflow patterns are very similar to the one obtained after perturbing the taphole diameter, but the effect is lesser on the tap duration. The slag level is seen to be strongly affected by the voidage change (through Eq. [8]).

Fig. 7

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) larger ($\varepsilon_{\text{h}} = \varepsilon = 0.39$) or (b) smaller ($\varepsilon_{\text{h}} = \varepsilon = 0.31$) coke-bed voidage. i = ir (red), i = sl (blue) (Color figure online)

The local conditions of the dead man part in front of the taphole strongly affect the pressure loss in the bed because of the converging flow. This is the main reason why the integration limit, $r_{ \hbox{min} }$, in the model is important. However, the conditions in front of the taphole are unknown in practice, and may also be subject to change because of accumulation of coke fines[4] or dissolution of the carbon in coke due to high liquid flow rates.[15,31] Furthermore, as the taphole drill breaks through the wall it affects the conditions both of the mushroom and the coke bed, inducing stochastic variations. To study the effect, the value of the radius of the taphole entrance void was changed to $r_{ \hbox{min} } = 0.075 \;{\text{m}}$ and $r_{ \hbox{min} } = 0.15 \;{\text{m}}$ with results illustrated in Figure 8. A small void region (cf. Figure 8(a)) increases the pressure drop in the bed, which elevates the liquid levels. It is worth noting that the iron level is raised considerably, and it lies above the taphole level throughout the tap. Thus, the iron-slag interface has to bend downward to let out slag, and this occurs after a slag delay of $t_{\text{sd}} = 20 \;{\text{minutes}}$. This is made possible by the inertial term of the Ergun equation, which results in a sufficient pressure loss created by the iron flow in the bed. As slag starts flowing out, the iron outflow rate drops slightly, but increases slowly during the rest of the tap. The slag outflow, in turn, increases strongly and linearly. By contrast, in the case where the taphole entrance void is larger (Figure 8(b)), the outflow order is interchanged: slag is the first phase to flow out ($t_{\text{sd}} = - \;5 \;{\text{minutes}}$) due to a low level of the iron-slag interface, which is at or below the taphole during the whole tap.

Fig. 8

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in): (a) smaller ($r_{ \hbox{min} } = 0.075\; {\text{m}}$) or (b) larger ($r_{ \hbox{min} } = 0.15\; {\text{m}}$) taphole entrance void. i = ir (red), i = sl (blue) (Color figure online)

Different Conditions at the Tapholes

In the practical operation, symmetry of the conditions at the alternating tapholes cannot be guaranteed as differences in the hearth state may arise due to spontaneous voidage changes caused by the accumulation or dissolution of fines, or liquid flow-path shifts caused by lining erosion or buildup of skull on the hearth wall and bottom. Asymmetry may also arise from a non-uniform supply of blast and auxiliary reductants to the raceways, or from channeling of the liquid supply from the upper part of the dead man. Particularly in large blast furnaces, with hearth diameters clearly above 10 m, impermeable zones may affect the liquid levels and the flows to the tapholes. Small-scale experiments[14,15] and simulations models[15,17,18,19] have been applied to study the expected results of such asymmetry. Roche et al.[22] studied the outflow patterns of iron and slag in a large three-taphole blast furnace and classified the normalized outflow share of slag by principal component analysis. The authors found large changes in the drainage from different tapholes, including strong imbalance and gradual changes in the outflow patterns.

With the aim of gaining understanding about the factors in the complex draining system that could lie behind such asymmetry, some cases were simulated with the model after imposing asymmetric conditions at the tapholes. Figure 9(a) shows the quasi-stationary state of the hearth for a furnace where the lengths of the two operating tapholes (subscripts 1 and 2) differ, i.e., $l_{{{\text{th}},1}} = 3 \;{\text{m}}$ and $l_{{{\text{th}},2}} = 2\;{\text{m}}$, and their corresponding taphole entrance levels in gray solid and dotted lines, respectively. Some imbalance is seen to arise, where the first taphole (TH1) that has the nominal length (solid lines), exhibits the same outflow patterns as in the Base case with unchanged duration, while the duration of taps from TH2 is clearly shorter (106 min). TH2 also drains more slag since the iron-slag interface lies below the taphole, but the short tap duration leaves the final iron level close to the level of TH1, which promotes iron flow when TH1 is opened.

Fig. 9

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in) with different taphole lengths ($l_{{{\text{th}},1}} = 3 \;{\text{m}}, l_{{{\text{th}},2}} = 2 \;{\text{m}}$): (a) same taphole diameters and (b) smaller diameter in TH2. Note that the inner ends of the two tapholes appear on different levels. i = ir (red), i = sl (blue) (Color figure online)

In practice, the effect of a short taphole can be counter-acted by selecting a smaller drill diameter. Since the taphole resistance is roughly proportional to the length and to the square of the velocity (and volume flow rate), we have $\Delta p_{\text{th}} \sim l_{\text{th}} d_{\text{th}}^{ - 4}$. Thus, a gross estimate of how to reduce the taphole diameter in the shorter taphole can be obtained. Denoting the desired (base-case) taphole length by $l_{\text{th}}^{*}$ and dimeter by $d_{\text{th}}^{*}$, we have $d_{\text{th}} = d_{\text{th}}^{*} \sqrt[4]{{\frac{{l_{\text{th}} }}{{l_{\text{th}}^{*} }}}} = 0.064 \;{\text{m}}\sqrt[4]{{\frac{2}{3}}} \approx 0.058 \;{\text{m}}$. Thus, the diameter of TH2 should be decreased by 6 mm. The liquid levels and outflows for the revised case are depicted in Figure 9(b), showing results that are quite similar to those of the Base case (cf. Figure 3(a)) The model predicts a small positive slag delay for TH1 and a negative one for TH2 due to their different levels. The tap durations are 158 and 148 minutes, and the slag share tapped from the two tapholes ($\gamma_{{{\text{out}},1}}$ and $\gamma_{{{\text{out}},2}}$) match the slag ratio in the inflow (Table II), so the taphole diameter correction has restored the balance.

Finally, two other sources of asymmetry are studied. Since the local voidage of the coke bed may vary with time, the role of a different voidage at the two operating tapholes was investigated by changing their values by ± 0.05 from the base-case value. It should be noted that the overall voidage of the dead man, $\varepsilon_{\text{h}}$, was assumed to be unaffected as the induced changes only concern the regions close to the tapholes, so the total liquid levels in Eqs. [1] and [2] are not affected directly but only the pressure drop in Eq. [8]—Figure 10(a) shows that a clear imbalance has arisen. The lower coke-bed voidage at TH1 ($\varepsilon_{1} = 0.30$) gives rise to a tap of short duration, because the tap-end condition of Eq. [17] is satisfied at an early moment due to the large value of ${{\Delta }}p_{\text{bed}}$. The longer duration of the tap from TH2 is the result of a combination of high starting liquid levels and low end levels (due to a low value of ${{\Delta }}p_{\text{bed}}$ in Eq. [17]). The different tap durations and different levels of the iron-slag interface at the moment when the taphole is opened lead to fundamentally different outflow patterns of the two liquids. Iron and slag start flowing out simultaneously and at practically equal normalized rates from TH1, and the rates of increase are not very different. The slag outflow from TH2, in turn, is delayed ($t_{{{\text{sd}},2}} = 20\; {\text{minutes}})$, after which it grows strongly and linearly.

Fig. 10

Iron and slag levels (z_ir, z_sl) and normalized outflow rates (m_i,out/m_i,in) for different coke-bed conditions at the tapholes: (a) different voidage ($\varepsilon_{1} = 0.4, \varepsilon_{2} = 0.3$) and (b) different size of taphole void regions ($r_{{{ \hbox{min} },1}} = 0.1 \;{\text{m}}, r_{{{ \hbox{min} },2}} = 0.15 \;{\text{m}}$). i = ir (red), i = sl (blue) (Color figure online)

The other reason for asymmetry studied is the extent of the taphole void region. By keeping the size unchanged at TH1, but extending it to $r_{ \hbox{min} } = 0.15 \;{\text{m}}$ at TH2, the state illustrated in Figure 10(b), showing some similarities, but also some differences, compared to the state after the bed-voidage change (Figure 10(a)). However, the slag level is lowered due to the smaller flow resistance, and also the iron level is shifted downwards. This yields a long tap duration for TH2, which lowers the iron level so much that there is a clear period of slag-only flow ($t_{{{\text{sd}},2}} = - \;8\; {\text{minutes}}$) as TH1 is opened. This taphole is characterized by a particularly strong initial outflow of slag. As a result of this, $\gamma_{\text{out}}$ is much higher in TH1 than in TH2, where the initial slag outflow rate is very low.

To gain a further understanding of the complex interaction of different factors on flow, the evolution of the main pressure-loss terms during the progress of the tap was analyzed. Figure 11(a) illustrates the contribution by the viscous (solid lines) and inertial (dashed lines) terms in Eq. [8] as well as the pressure drop in the taphole (black line, right ordinate scale) for the Base case. Iron and slag have been depicted by red and blue lines for the coke-bed pressure drop. The taphole is seen to represent the clearly largest term (218-270 kPa). This loss term increases slightly initially, but shows a decrease during the second part of the tap, largely due to taphole erosion which lowers the velocities. In the hearth, the inertial term is the clearly dominating one for iron, due to a low viscosity and high density. For slag, the viscous term is more important, but the role of the inertial term grows along with the increasing slag outflow.

Fig. 11

Pressure-drop terms in the coke bed (Eq. [8]) and in the taphole (Eq. [13]): (a) Base case, as well as (b) drainage from TH1and (c) TH2 for the case with asymmetric size of the taphole entrance void region, $r_{ \hbox{min} }$ (cf. Figure 10(b))

The corresponding terms for the asymmetric case where $r_{ \hbox{min} }$ for the two tapholes differ (cf. Figure 10(b)) are depicted in the lower two panels of Figure 11. TH1 (Figure 11(b)) shows a lower pressure drop in the taphole. The strong initial slag outflow during the first minutes yields higher viscous and inertial losses in the bed, which suddenly decrease when iron starts flowing out. Simultaneously, the pressure drop in the taphole increases abruptly (by about 40 kPa), balancing the change. For the remaining parts of the tap, the behavior is quite similar to that of the Base case, but the shorter draining time limits the erosion of the taphole and hence also the loss terms. For TH2 (Figure 11(c)), the larger radius of the taphole void region ($r_{{{ \hbox{min} },2}} = 0.15 \;{\text{m}}$) results in smaller pressure losses in the hearth, but the strong initial iron outflow during indicates the role of the inertial term.

Dynamic Effects

Even though the primary aim is to keep the conditions in the hearth as stable as possible, occasional events or disturbances temporarily perturb the state. It is therefore interesting to use the model to analyze the dynamic response of the hearth. Some examples of the dynamic behavior of the liquid levels and outflows are therefore presented, inspired by the findings in the analysis of process data from the reference blast furnace (cf. Section IV). It should be noted that short-term dynamics (e.g., acceleration of the fluids) are disregarded, and that base-case settings (Table I) were used for all variables and parameters, except the perturbed quantities.

In some situations, it is not possible to open the taphole due to external constraints (e.g., runner maintenance problems or lack of torpedo cars) and if the expected duration of the disturbance is short, the blast volume is not decreased. Figure 12 shows a case where the hearth was run into a quasi-stationary state before a disturbance was introduced by keeping the taphole plugged 14 minutes longer than the base-case value between the first and second tap; the taps in the figure have been numbered for convenience. The outflows show that iron is the first phase to flow out ($t_{\text{sd}} = 17\; {\text{minutes}}$), the slag ratio of the tap is lower ($\gamma_{\text{out}} = 0.17$), and the maximum iron and slag levels are elevated by about 0.15 and 0.6 m, respectively. The resulting tap lasts about 10 minutes longer, giving time for the iron to descend to practically the same vertical level as after a “normal” tap. Therefore, the system rapidly re-assumes its original quasi-stationary state. A somewhat more complex disturbance is introduced after the third tap in the figure, where the production rate (dashed lines) is decreased linearly within two hours to $8120 \;{\text{t}}/{\text{day}}$, kept at this level during six hours, and increased linearly back to the original level in 4 hours. For simplicity, the furnace gauge pressure ($p_{\text{gas}} - p_{0}$) was decreased in proportion to the production rate. The decreased production rate results in a substantial descent of the liquid levels in the hearth and in shorter durations of the taps. As the iron level descends, the share of slag in the outflow increases (to a maximum of $\gamma_{\text{out}} = 0.26$ for the sixth tap), but when the production rate increases, the opposite occurs, and the share of slag in the outflow decreases (to a minimum of $\gamma_{\text{out}} = 0.17$ for the ninth tap). At the end of the depicted period, the system is back in its normal quasi-stationary state.

Fig. 12

Liquid levels (z_ir and z_sl) and inflow and outflow rates (dashed and solid lines) of iron and slag (m_ir and m_sl). Inter-cast period between taps #1 and #2 is prolonged from 6 to 20 min. Production rate is decreased after tap #3, kept lower for 6 h, and then increased linearly back to the original level in four hours. Base-case setting of all other variables

The final example of dynamics studies the effect of a 3.5-hour stoppage and a longer inter-cast period between taps #3 and #4. With reference to the lower panel of Figure 13, the furnace pressure is decreased linearly within two hours (after $t = 1000\; {\text{minutes}}$), kept at the ambient pressure during two hours, and ramped up to the normal furnace pressure in three hours. To consider the time lag of the liquids between the tuyere level and the hearth, the production rate was varied proportionally to the gauge pressure with a delay of 30 minutes. The taphole was kept closed until 1.5 hours had elapsed after the pressure started to increase.

Fig. 13

Liquid levels (z_ir and z_sl) and inflow and outflow rates (dashed and solid lines) of iron and slag (m_ir and m_sl). The production is ramped down and up prior to and after a 3.5-h stoppage, respectively. A longer inter-cast period occurs between taps #3 and #4. Base-case setting of all other variables

The outflows show interesting “deformed” patterns for the last tap (#2) before the stoppage, due to the decrease in liquid inflows and furnace pressure. The first tap after the stoppage (#3) has a strong iron outflow and a clear slag delay ($t_{{{\text{sd}} }} \approx 50 { \hbox{min} }$). Hence, this tap drains considerably less slag ($\gamma_{\text{out}} \approx 0.16$). The longer inter-cast period that follows delays the slag outflow of the next tap (#4) even more ($t_{{{\text{sd}} }} = 57 { \hbox{min} }$) and extends its duration to almost $t_{{{\text{tap}} }} = 180\,{ \hbox{min} }.$ The slag share rises slightly and in the fifth tap it is $\gamma_{\text{out}} = 0.25$. After this, the value gradually decreases towards $\gamma_{\text{in}}$. The outflows can be better understood by studying the liquid levels in the upper panel of Figure 13. In the final tap (#2) before the stoppage, the liquids descend to low levels, but the levels increase considerably during the period when the production has commenced but the tapholes are kept closed (black lines). The high iron level gives rise to a slag delay of tap #3. Due to the long inter-cast period that follows between taps #3 and #4, the slag level raises further, yielding a long tap (#4) during which the iron level descends well below the taphole. This is the reason why two taps (#3 and #4) with $\gamma_{\text{out}} < \gamma_{\text{in}}$ are followed by taps with $\gamma_{\text{out}} > \gamma_{\text{in}}$.

Outflows in a Three-Taphole Blast Furnace

This section presents a comparison with some of the findings of the simulation study with process data from BF 7 of Tata Steel Europe in IJmuiden, the Netherlands, which is a large ($d_{\text{h}} = 14 {\text{m}}$) three-taphole blast furnace. In this furnace, the outflow rates of iron and slag are “measured” by differencing of results from frequent weighing of the torpedoes and measurement information from the slag granulation units. The former signal is considered fairly accurate, while the latter is known to be more uncertain.[23] Despite potential inaccuracies, the signals reported in the historical database of the steel plant were used as such in this study. In analyzing the results, one should keep in mind that time lags caused by the main trough and runner may occur. The refractory state during the present campaign was estimated by an inverse heat-transfer model,[32] and based on this hearth geometry a force balance was stated and solved, indicating that the dead man is likely to sit in BF7.[33]

The outflows from the furnace was analyzed by Roche et al.[18] for a three-month period from early 2016 holding more than 800 taps. The data set, together with another more extensive one (> 1400 taps), was later studied in a classification of the liquid outflow patterns by principal component analysis.[22] These studies demonstrated that the outflow patterns may change gradually or abruptly, and that imbalance between the two operating tapholes may occur. Figure 14 shows the slag delay for the taps during the former data period. The values were calculated by noting the time difference between the moments when slag and iron started flowing out for every tap. For about 15 pct of the taps, the reported outflows were so irregular that a slag delay could not be determined, and the value was assumed to be zero for these. The figure illustrates that there are very few positive delays except very small ones ($t_{\text{sd}} \in \left( {0,2} \right] { \hbox{min} }$), which may be apparent ones due to the delays of the liquids in the trough and runners, and large ones due to longer inter-cast periods or stoppages (cf. Figures 12 and 13). By contrast, the negative slag delays were frequent and exhibited certain patterns.[18,22,23] For instance, there were periods (around taps 180, 225, 420 and 580 in Figure 14) where one taphole drained slag first while in the other the liquids started flowing out simultaneously, or there was a slag delay of 1-2 minutes). Such imbalance was found to appear and disappear suddenly, e.g., in conjunction with taphole changes, or gradually with time.[34]

Fig. 14

Observed slag delays in the reference furnace for a 3-month period

Figures 15(a) through (c) show the (slightly filtered) normalized outflow rates of six consecutive taps with alternating tapholes. The first taphole (TH1, left column) drains slag first at a rate at least twice the production rate. The slag delay reported in the lower right corner of the panels falls in the range $t_{\text{sd}} \in \left[ { - 10, - 3} \right] { \hbox{min} }$. Throughout the taps, slag is the dominating liquid (expressed in this normalized way) drained from this taphole, with a share of $\gamma_{\text{out}} \approx 0.26$. By contrast, iron and slag start draining at the same time from the other taphole (TH2, right panels) and the share of slag is much lower ($\gamma_{\text{out}} \approx 0.11$). Another example from a later period is given by the pair in Figure 15(d), where the differences in the slag share are smaller. It is interesting to compare these patterns with the simulated ones, and particularly with those of Figure 10(b), which have been reproduced in Figure 15(d). Thus, as proposed earlier by the present authors,[22,23,34] the conditions at the inner end of the taphole may explain the draining imbalance without further differences in permeability of the dead man as suggested in earlier studies.[15,18]

Fig. 15

(a through d) Normalized outflows of iron (red) and slag (blue) for two sets of consecutive taps of the reference furnace using alternating tapholes, showing a clear imbalance in iron and slag drained and (e) simulated flows for different $r_{ \hbox{min} }$ reproduced from Fig. 10(b) (Color figure online)

Also other features of the simulated outflows are observed in the measurements from the furnace. The taps in Figures 16(a) and (b) resemble the simulated outflow patterns for several different cases, e.g., those for smaller taphole diameter or smaller coke bed voidage, shown in Figures 16(c) and (d), respectively (reproduced from Figures 6(a) and 7(b)). The trends seen in the two consecutive taps in Figure 17(a) resemble those for the simulated system with different taphole lengths, shown in the Figure 17(b) (reproduced from Figure 9(a)).

Fig. 16

Normalized outflows of iron (red) and slag (blue): (a, b) two single taps and similar outflows for the simulated system with (c) smaller $d_{\text{th}}$ and (d) bigger ε_h taken from Figs. 6(a) and 7(b) (Color figure online)

Fig. 17

Normalized outflows of iron (red) and slag (blue): (a) a pair of consecutive taps and (b) simulated for the case with different $l_{\text{th}}$ taken from Fig. 9(a) (Color figure online)

Finally, a comparison of the dynamic response of the reference furnace hearth with the simulated counterpart is made, starting with the disturbances already studied in Figure 12. Figure 18(a) shows the effect of a longer inter-cast period of about 20 minutes (clearly longer than the average, which is 6 minutes) before tap #363. The slag delay of the tap is of the same order as the prolonged inter-cast period, in agreement with the findings presented in Figure 12. The effect of a reduction and increase in the blast volume, which was found to be a recurring event in the process data analyzed, is seen in Figure 18(b), Even though the outflow rates vary considerably from tap to tap, a common feature with the simulated counterpart presented in Figure 12 is that the share of slag increases in the outflow for the period when the production rate is low.

Fig. 18

Inflow and outflow rates (dashed and solid lines) of iron and slag for two sets of consecutive taps from the reference furnace: (a) effect of longer inter-cast time and (b) effect of temporary decrease in production rate

The drainage at a stoppage is presented in Figure 19, where the evolution of the production rate is similar to the one used in the simulation of Figure 13. Comparison of the outflows of the figures reveals several common features, despite some discrepancies. The simulated iron outflow before the stoppage (for tap #408) resembles the simulated counterpart, while the slag outflows differ. For the two taps after the stoppage (#409 and #410) the observed slag delays are similar to those in Figure 13, and the iron outflow rate is clearly above the production rate (dashed red line). In conclusion, the similarities are encouraging, demonstrating the general feasibility of the model.

Fig. 19

Inflow and outflow rates (dashed and solid lines) of iron and slag for consecutive taps, including a 3.5-h stoppage for the reference furnace

Conclusions and Future Work

A simulation model of the draining of the hearth of a multi-taphole blast furnace has been developed. The model is based on basic fluid mechanics and a set of simplifying assumptions that are justified for the system under study. It describes the evolution of the overall levels of iron and slag in the hearth and the outflow rates of the two liquids during tappings of the furnace. Special attention was paid to describing the region in front of the taphole to be able to consider the pressure drops of iron and slag, which is a prerequisite of modeling the outflows. The arising model has been illustrated by a set of examples, where the sensitivity of the simulated liquid levels and outflows is studied with respect to changes in the conditions and to some model parameters. Asymmetry that arises if the conditions at/of the two alternating tapholes are different has also been studied, as well as the system’s dynamic response to disturbances. To verify the model, the liquid outflow rates measured in a reference blast furnace were used for comparison, revealing that several of the simulated outflow patterns also occurred in the real process, including strongly asymmetric performance of the two operating tapholes with respect to slag drainage and outflow order of the liquids. The model has demonstrated the important role played by the taphole length and diameter, as well as the internal conditions (e.g., bed voidage) and in particular the state of the coke bed in front of the taphole, where a majority of the pressure losses in the bed are located. The sensitivity analysis has demonstrated that the duration of the tap may vary up to one hour and that the share of slag tapped from the alternating tapholes in case of asymmetry may differ substantially.

Overall, it can be concluded that the model relatively successfully reproduces the drainage patterns observed in the real process. Because the model is fast, it is possible to study a multitude of both quasi-stationary and dynamic cases of interest. The operating point of the hearth was found to be robust, so the dynamic response to short disturbances usually brought the hearth back to its original state in five taps. This indicates that the important features of the fluid mechanics have been captured relatively well. The model has been able to explain why taps in the reference furnace often show no slag delay (i.e., both liquids start flowing simultaneously) and why negative slag delays are clearly more frequent than positive ones (the latter ones usually being the result of longer inter-cast periods). The model also explains why taps that start with slow iron flow only (clearly below the production rate) may still drain slag after a few minutes, even though the iron level rises: the pressure loss in the iron flow in front of the taphole is sufficient to bend the iron-slag interface down to let out also slag. It has also been demonstrated that the slow initial outflow of iron in taps that start with slag is a result of two factors associated with a low iron level: the narrow path through which iron has to flow (cf. Figure 2) increases the velocity and therefore the pressure loss, and the head difference (i.e., $- g\rho_{\text{ir}} z_{\text{ir}}$ in Eq. [4]), which decreases the driving pressure difference imposing the flow. Furthermore, it has been demonstrated that the conditions at the entrance of the taphole can explain why asymmetry arises in the draining of slag from two alternating tapholes, without the occurrence of impermeable zones in the more central parts of the dead man.

Naturally, some challenges still remain to be tackled in the model. One is that there is a number of model parameters that have simply been given “suitable” values without a solid theoretical or practical justification. In experimenting with the parameters, it was found that similar drainage patterns could be obtained for different combinations of the model parameter values. Thus, another set of parameter values than those used in the present work may be more appropriate. A complication in the verification of the model is the large variations in the drainage observed in the real process. Obviously, many stochastic matters influence the outflows. For instance, viscous fingering[35] is known to play a role in the final phases of slag drainage, and may make taps much shorter than expected based on the overall liquid levels. Another problem is that the outflows rates of iron and slag are not available in many plants, and where available, at least the slag measurement is inaccurate and difficult to calibrate. Likewise, the liquid levels cannot be measured directly, and indirect techniques, such as emf and strain gauges,[36] are susceptible to noise and drift, which makes it hard to verify the model’s results.

The general findings and the drawbacks noted above indicate some directions for future work. The mismatch between the observed and simulated outflows that occurred in certain situations could be addressed by revising the formulation of the pressure-loss equations, and particularly those concerning the entrance loss. Since the drainage patterns in the reference furnace were sometimes found to show gradual changes,[22,34] it would be natural to develop the model to automatically adapt to the observed drainage patterns and in this way provide a physical on-line explanation of the hearth state. Another interesting application of the model is to use it for finding ways to balance the outflows if asymmetric taps occur. In furnaces with a high sump depth, the model could also be extended to consider a possible floating of the dead man by a simple revision of the liquid-level equations.[10,12] Finally, if the model is applied to furnaces using overlapping taps, the logical conditions concerning the shifts between the number of phases being drained should be revised.