Introduction

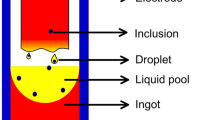
The vacuum arc remelting (VAR) process is extensively used to purify numerous alloys such as stainless steel, Nickel-based, and Titanium-based alloys. It is a method of refining an impure alloy (electrode in VAR) through vacuum as heated by a DC arc. The tip of the electrode melts resulting in the formation of droplets. Afterward, droplets drip through the vacuum and reach the molten pool. The molten pool solidifies in a water-cooled mold to build the high-grade, ultraclean alloy as schematically shown in Figure 1(a). Droplets carry low-density oxide inclusions to the molten pool. Inclusions are transferred to the solidification rim (more precisely the surface of ingot) near the mold. Furthermore, unfavorable elements with high vapor pressure such as Pb, Sn, Bi, Te, As, and Cu are evaporated under vacuum conditions. Some of those elements may condensate on the mold wall.

Fig. 1
figure 1

(a) Schematic representation of VAR process and its main components, (b) A cross section of the VAR process is illustrated to indicate different regions and corresponding interfaces/boundaries. Calculations are carried out considering a 2D axisymmetric model

Full size image

Modeling VAR process is very challenging and controversial as the process involves a wide range of physical phenomena and their interactions. Modeling activities are required to study each phenomenon including formation and movement of cathode spots at the tip of electrode,[1,2,3,4,5,6,7] the vacuum plasma,[4,5,8,9,10,11,12,13,14,15,16,17,18,19,20] the electric current transferred directly between the electrode and mold, known as “side-arcing,”[12,18,21,22,23,24] the thermal radiation in the vacuum region,[21,25,26] melting of the electrode,[8,27,28,29,30,31,32,33,34,35,36,37,38] the influence of electromagnetic field on the flow known as magnetohydrodynamics (MHD) in the molten pool,[39,40,41,42,43,44,45,46,47,48] and the solidification of the ingot.[44,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] To attain a deeper understanding of modeling challenges, a brief description is given for each of those phenomena in the following.

Cathode spots with the sizes in the range of 1 to 100 μm are the centers of plasma production from where electrons/ions are emitted to the vacuum plasma region. Each cathode spot carries a tremendous amount of electric current (~ 1010 to 1012 A m−2), where the temperature is remarkably high (~ 1-1.2 eV corresponds to 11,000 K to 14,000 K).[4] Formation and movement of the cathode spots are described by self-similarity (Fractal) model in quantum mechanics. In this approach, the movement of the spots is assumed to be governed by a combination of the stochastic random motion and a drift in the retrograde direction.[64] A tremendous number of models were presented to study cathode spots in the presence/absence of and external magnetic field for different materials which are described in Reference 4.

The behavior of the vacuum plasma plays an important role in the quality of the final ingot. Two modes of arcs are recognized, namely diffusive and constricted.[17] Cathode spots occupy the entire surface of electrode in the diffusive mode. In contrast, they form a cluster on a small fraction of the surface of electrode to eject a narrow column of the constricted arc. In the VAR process, the desired arc mode is a diffusive arc to ensure relatively smooth/uniform distribution of heat flux to the molten pool. Formations of freckles and other solidification defects in VAR are often reported to be related to a constricted arc.[65] The probability of the formation of a constricted arc increases as the gap length increases.[1] Furthermore, an external magnetic field can significantly influence the behavior of the arc including the arc radius and speed.[11,16] Research attempts to model plasma generation and expansion in VAR process are minimal.[5,20] Chapelle et al.[20] pointed out that plasma is rapidly ionized and expands in the vacuum plasma region. Furthermore, the friction between ions and electrons accelerates the plasma jet. Traditionally, a Gaussian distribution of electric current density as a function of radial position (r) is specified on the top surface of ingot to model the effect of arc in VAR that will be further described in Section II–A–1.

As a consequence of the high reactivity of the involving materials of ingot and mold in VAR, side-arc becomes a safety-critical parameter as they transfer a large amount of energy. Side-arcs can be easily observed as a glow in the annulus region between the electrode outer wall and the crucible inner wall during operation.[12] Williamson et al.[24] pointed out that a sudden increase in the amplitude of the voltage is associated with the side-arc. A significant portion of the total imposed electric current (~ 30 to 70 pct) is carried by side-arcs especially through the metal crown at the top of ingot surface.[23] In the presence of an external magnetic field, the arc is confined below the electrode that in turn reduces the amount of side-arcing.[12] Presently, the relationship between the amount of side-arcing and the gap length is unknown.[23] To the best of our knowledge, no model was presented to study the influence of the amount of side-arcing on the transport phenomena in the molten pool.

The radiative heat exchanges among the electrode, ingot, and mold are dependent on the configuration of the process including the electrode diameter and mold diameter (more precisely fill ratio) and the gap length.[26] With the increasing fill ratio and the decreasing gap length, the energy loss to the mold through radiation decreases. Furthermore, the number of side-arcs significantly alters the radiation heat balance in the vacuum zone.[21]

The melt rate of the electrode is governed by the gas pressure inside vacuum chamber, the arc power and gap length.[28,33] The tip of electrode is superheated (~ 150 K to 250 K) during operation.[28] A large thermal gradient was noticed in the vicinity of the electrode tip (~ 1 mm) where a liquid film of the alloy exists.[33] Of note, presence of a crack on the electrode significantly impacts the behavior of the arc and consequently the melt rate of the electrode.[28,66] The mechanism of droplet transfer from the tip of melting electrode to the molten pool is dependent on the gap length. Chapelle et al.[36] postulated three steps including growth, rupture, and erosion of metallic droplets when the gap length is large. Furthermore, they found that the voltage signal is associated with the metal transfer mechanism. Growth of metal, arc extinction (drip short), arc reigniting, explosion of elongated metal, and erosion of the left over protuberance were detected on the voltage signal when the gap length is short.[33]

The flow field in the molten pool impacts the solidification behavior (e.g., macrosegregation, pool profile, etc.) of the ingot. The distribution of arc (diffusive or constricted) on the surface of ingot influences the flow field in the molten pool.[40] The turbulent flow in the molten pool is driven by thermosolutal buoyancy and Lorentz force which originates in the self-induced and external magnetic fields.[40] Davidson et al.[48] numerically studied the flow in the molten pool. They reported that modest changes in the amount of imposed current or weak variations in the external magnetic field can dramatically alter the flow pattern in the molten pool of VAR.

A large amount of research has been ongoing to explore the solidification structure and macrosegregation of a VAR ingot.[49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] Formations of surface ring pattern structures, tree-rings, columnar to equiaxed transitions were reported for various types of VAR ingots. Furthermore, solidification defects such as white spots and freckles were observed. Revil-Baudard et al.[67] pointed out that the imposition of an external magnetic field helps to diminish the solidification defects especially macrosegregation.

Conventionally, the molten pool profile is used as an indicator for the internal quality of the solidified ingot. A shallow molten pool is desirable to promote unidirectional solidification of the ingot and consequently to build a segregation-minimal alloy.[68,69] Here, we propose a model to study transport phenomena such as electromagnetic, thermal/solidification, and flow fields in VAR. The sensitivities of modeling results concerning the distribution of arc in the vacuum region mostly on the top surface of ingot, the side-arcing, and helium gas cooling of the ingot surface are analyzed. For this purpose, an extensive series of simulations were performed.

In the present study, the electromagnetic field is calculated in the entire system including the electrode, vacuum arc, ingot, and mold. The model accounts for the influence of electromagnetic field on the flow in the molten pool through Lorentz force. In addition, radiation heat transfer in the vacuum plasma region as well as heat transfer at air gap (with and without helium gas cooling) is taken into account. The solidification of the ingot considering a Titanium-based (Ti-6Al-4V) alloy is calculated. Experimental results regarding the marked molten pool profile are utilized to validate the model. The main goal is to obtain some fundamental understanding of the VAR process through the numerical modeling. Improvement of our knowledge on the role of the aforementioned phenomena (e.g., side-arcing) can aid engineers to optimize the process design and operation parameters.

Modeling

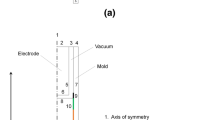
The well-established finite volume method (FVM) is applied for numerical simulation of the flow field, electromagnetic field, heat transfer, and solidification in VAR. The commercial CFD software, ANSYS FLUENT v.14.5, was employed to carry out simulations. User-defined functions (UDFs) are implemented for special modeling equations e.g., to model arc, solidification, etc. Over the last decade, authors of the present study developed numerous models for the conventional electroslag remelting (ESR) process.[70,71,72,73] The model features as the base for the present study were experimentally verified. From modeling point of view, the major difference between the standard ESR and VAR processes is the substitution of the slag by the vacuum plasma. Here, a 2D axisymmetric model is proposed. Illustratively, a cross section of the VAR process is shown in Figure 1(b), where different region and boundaries are marked.

The following assumptions are made for all simulation trials:

  1. (i)

    The electromagnetic field is determined regardless of the thermal, plasma, and flow fields. In other words, one-way coupling is considered: the thermal, plasma, and flow fields do not influence the electromagnetic field.

  2. (ii)

    At the top edge of the VAR ingot where the as-solidified shell is still ‘soft,’ a good contact with the mold is assumed. The length of the contact zone (20 mm) is predefined. Afterward, the as-solidified shell shrinks away from the mold, and the ingot–mold contact gets lost to form an air gap. This air gap is treated by considering an effective heat-transfer coefficient.[70] The latter is influenced by helium gas cooling which is further described in Section III–B–3. The impact of metal crown at the top edge of ingot on the electromagnetic field is taken into account. The length of crown is prescribed (20 mm).

  3. (iii)

    The top surface of ingot is assumed to be flat and stationary.

  4. (iv)

    The formation of droplets at the tip of electrode and their motion at the vacuum region are not tracked. The impact of droplets on the global electromagnetic field is ignored. However, the influence of droplets on the momentum, energy, and mass transfer in the molten pool is implicitly modeled as source terms in corresponding conservation equations. The latter is extensively described in Reference 74.

  5. (v)

    The arc is implicitly modeled considering a Gaussian distribution of electric current density as a function of radial position (r) on the top of surface of ingot/tip of electrode that will be further described in Section II–A–1. The self-induced magnetic field is assumed to be dominantly azimuthal. No external magnetic field is considered.

Governing Equations

Electromagnetic field

The A-ϕ formulation is utilized to determine the electromagnetic field,[75,76] where ϕ denotes the electric scalar potential and A is the magnetic vector potential. The method is very robust and accurate to model the current path including side-arcing. The electric scalar potential is obtained by solving the conservation equation of electric current:

$$ \nabla \cdot \vec{j} = 0 $$
(1)

The current density (j) is composed of two parts:

$$ \vec{j} = - \sigma_{{}} \nabla \varphi - \sigma \frac{{\partial \vec{A}}}{\partial t} $$
(2)

where (σ) denotes the electrical conductivity of material.

The magnetic field (B) is calculated based on the vector potential formulation:

$$ \vec{B} = \nabla \times \vec{A} $$
(3)
$$ \vec{j} = \nabla \times \left( {\frac{1}{{\mu_{0} }}\nabla \times \vec{A}} \right) $$
(4)
$$ \nabla \cdot \vec{A} = 0 $$
(5)

The magnetic permeability (\( \mu_{0} \)) in Eq. [4] is assumed to be constant (\( 4\pi \times 10^{ - 7}_{{}} J \cdot m^{ - 1} \cdot A^{ - 2} \)) in all regions. Furthermore, the Coulomb gauge (Eq. [5]) is applied to obtain a unique solution.[75]

Eventually, Lorentz force (\( \vec{F}_{L} \)) is explicitly computed and added as source term to the momentum conservation equations:

$$ \vec{F}_{L} = \vec{j} \times \vec{B} $$
(6)

Special care must be taken to model the electromagnetic field in the vacuum region.

Electrode tip, electrode–vacuum interface, vacuum–mold interface, crown, and ingot top surface are modeled as conjugate walls (Figure 1(b)) where the flux of electric potential (≈ electric current density) must be specified. The flux at electrode–vacuum interface and vacuum–mold interface are set to zero. However, the flux at crown (\( \vec{j}_{\text{crown}} \)) is dependent on the amount of side-arcing as follows:

$$ j_{\text{crown}} = \frac{{I_{0} f_{\text{side - arc}} }}{{A_{\text{crown}} }} $$
(7)

where \( A_{\text{crown}} \) denotes the area of crown, and \( f_{\text{side - arc}} \) is the fraction of the total imposed current (\( I_{0} \)) which flows through the crown. Following Pericleous et al.,[77] Kelkar et al.,[78] and Spitans et al.,[79] a Gaussian distribution of electric current density as a function of radial position (r) is specified at electrode tip (\( \vec{j}_{\text{tip}} \)) and ingot top surface (\( \vec{j}_{\text{ingot - top}} \)) as follows:

$$ j_{\text{tip}} = \frac{{I_{0} \exp \left( { - \frac{{r^{2} }}{{R_{\text{a}}^{2} }}} \right)}}{{\int_{0}^{{R_{\text{e}} }} {2\pi r\exp \left( { - \frac{{r^{2} }}{{R_{\text{a}}^{2} }}} \right){\text{d}}r} }} $$
(8)
$$ j_{\text{ingot - top}} = \frac{{I_{0} (1 - f_{\text{side - arc}} )\exp \left( { - \frac{{r^{2} }}{{R_{\text{a}}^{2} }}} \right)}}{{\int_{0}^{{R_{\text{i}} }} {2\pi r\exp \left( { - \frac{{r^{2} }}{{R_{\text{a}}^{2} }}} \right){\text{d}}r} }} $$
(9)

In Eqs. [8] and [9], \( R_{\text{e}} \)is electrode radius, and \( R_{\text{i}} \) is the radius of the ingot. The radius of arc (\( R_{\text{a}} \)) is considered as a fraction (\( f_{\text{R}} \)) of ingot radius,

$$ R_{\text{a}} = f_{\text{R}} R_{\text{i}} $$
(10)

The flux of electric potential at other exterior boundaries (i.e., vacuum top, mold bottom, ingot bottom, and mold–water interface) is zero, whereas the value of electric potential is set to zero at mold top. The flux of electric potential at the top of electrode (\( \vec{j}_{\text{electrode - top}} \)) is specified as a function of electrode cross-sectional area (\( A_{\text{electrode}} \)) as follows:

$$ \vec{j}_{\text{electrode - top}} = - \frac{{I_{0} }}{{A_{\text{electrode}} }} $$
(11)

All fluxes of electric potential are specified in the vacuum zone that makes the electric potential field and consequently the electric current density field independent of the electrical conductivity of the vacuum plasma in the vacuum plasma region.

Continuity of the magnetic potentials is applied at all interior boundaries.[80] The magnetic induction flux is set to zero at mold bottom, ingot bottom, and mold–water interface. In addition, zero flux of magnetic induction is applied at electrode top, vacuum top, and mold top.[80]

Flow field

The feeding velocity is known for the melting electrode where the velocity in the axial direction is specified (1.15 mm s−1). The flow field is solved in the ingot zone. The continuity and momentum equations are used to determine the velocity field (\( \vec{u} \)):

$$ \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \vec{u}) = 0 $$
(12)
$$ \frac{\partial }{\partial t}(\rho \vec{u}) + \nabla \cdot (\rho \vec{u}\vec{u}) = - \nabla p + \nabla \cdot (\mu_{\text{eff}} (\nabla \vec{u} + \nabla \vec{u}^{T} )) + \rho_{0} \vec{g}\beta (T - T_{0} ) + \vec{F}_{L} $$
(13)

where \( \mu_{\text{eff}} \) denotes the effective viscosity, \( p \)is the pressure, \( \vec{g} \) is the gravity constant, \( \beta \) is the thermal expansion coefficient, and \( \rho_{0} \) and \( T_{0} \) are the reference density and reference temperature, respectively, to calculate thermal buoyancy according to Boussinesq approximation.

The turbulence is computed based on the Scale-Adaptive Simulation (SAS) model.[81,82] SAS model is an effective and accurate turbulence model especially for near-wall treatment as the model is insensitive to the grid spacing of the near-wall cells.[81] The accuracy of the results using the SAS model is comparable to that of the LES model with the advantage of lower computational cost. Details of the model are described in References 81 and 82.

The interdendritic flow inside the ingot mushy zone is modeled according to Darcy’s law.[83] The isotropic model of Kozeny–Carman is utilized to estimate the drag resistance of dendrites against the flow in the mushy zone.[79,84]

Non-slip boundary condition is applied at all boundaries except for ingot top surface where a free-slip condition is applied. In addition, the velocity is specified to the casting speed (\( u_{\text{s}} \)) at the ingot bottom.

Thermal field and solidification

The temperature field is calculated by solving an enthalpy (h) conservation equation:

$$ \frac{\partial }{\partial t}(\rho h) + \nabla \cdot \left( {\rho \vec{u}h} \right) = \nabla \cdot (\lambda_{\text{eff}} \nabla T) + S. $$
(14)

In Eq. [14], \( \lambda_{\text{eff}} \) is the effective thermal conductivity including the effect of turbulence, T is temperature, and S denotes the source term for treating the solidification latent heat as follows:

$$ S = - \frac{\partial }{\partial t}(\rho Lf_{\text{l}} ) - \rho L\vec{u}_{\text{s}} \nabla f_{\text{l}} $$
(15)

Hear, \( f_{l} \) is the liquid volume fraction, and L denotes the heat of fusion.[85]

Through Eq. [16], the liquid volume fraction is estimated as a function of temperature,[79]

$$ f_{\text{l}} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {T > T_{\text{liq}} } \hfill \\ {(T - T_{\text{sol}} )/(T_{\text{liq}} - T_{\text{sol}} )} \hfill & {T_{\text{sol}} < T \le T_{\text{liq}} } \hfill \\ 0 \hfill & {T \le T_{\text{sol}} } \hfill \\ \end{array} } \right. $$
(16)

Radiation heat transfer in the vacuum plasma region is a complex phenomenon.[26] Herein, a computationally efficient and straightforward approach based on the P-1 radiation model is employed. The absorption and scattering coefficients are set to zero, whereas a value of one is applied for the refractive index. A detail of the model is described in References 86 and 87 Influences of the arc and metallic droplets on the radiation heat balance are ignored. To apply the model, the temperature of the electrode tip must be known a prior. The latter can be experimentally measured during the operation, and it is reported to be around 150 K to 250 K above the liquids temperature of the alloy.[24] As such, the magnitude of temperature (Tliq+200 K) is specified in the present study.

The thermal boundary conditions at the ingot, and mold boundaries are assigned.[70,71,72,73,74] The radiation heat transfer with or without gas cooling is taken into account at the air gap[70] that is further elucidated in Section III–B–3. The contact area is considered at the ingot–mold interface as well as the electrode top so that the heat-transfer coefficient (500 W m−2 K−1) is specified.[34,88] Furthermore, the heat-transfer coefficient (7000 W m−2 K−1) at mold–water interface is prescribed.[70,71,72,73,74]

Other Settings

Hosamani et al.[58,89] conducted several experiments to study influence of various parameters such as the amount of imposed current, gap length, gas cooling on a VAR ingot of several alloys like Titanium-based, Nickel-based, etc. In the present study, the numerical model is configured based on their experiment on Ti-6Al-4V alloy.

For our simulations, we considered reported values of material properties in the literature which are temperature dependent. Those values are extracted from References 90,91,92,93,94. The material properties of the alloy as well as operating conditions are listed in Table I.

Table I Alloy Properties (Ti-6Al-4V) and Operating Conditions
Full size table

Results

Transport Phenomena in VAR

Here the capability of our proposed model to capture transport phenomena including flow, thermal/solidification, and electromagnetic fields is demonstrated. As previously mentioned, the distribution of arc in the vacuum plasma region is dependent on the arc radius and the amount of side-arcing. Those parameters are chosen within the reported values. The amount of side-arcing is 50 pct of the total imposed current. In addition, the ratio of arc radius to the ingot radius is 0.7. The sensitivity of modeling results to the aforementioned parameters is further elucidated in Section III–B. Field structures are illustrated in Figure 2. The magnetic field is strong in the vacuum plasma region where the arc exists. As a consequence of side-arcing and mold current at ingot–mold interface, a nonuniform distribution of the magnetic field at molten pool is observed as shown in Figure 2(b). The magnetic field as well as electric current density is strong at the top of molten pool near the mold wall. The interplay between the magnetic field and electric current density creates a strong Lorentz force that drives the flow in a clockwise direction. The rigorous mixing of the flow results in a relatively uniform temperature field in the molten pool. A significant portion of input energy (~ 60 pct) to the system is carried by droplets to the molten pool. Furthermore, a notable amount of energy (~ 20 pct) is lost to the mold wall due to radiation at vacuum plasma region.

Fig. 2
figure 2

Field structures for the VAR considering the following parameters to model the distribution of arc in the vacuum plasma region: (Ra = 0.7 Ri) and (Is = 0.5 It). (a) Contour of the electromagnetic field including magnetic flux density (left half) and electric current density (right half); (b) Velocity field (left half) and thermal field (right half). In each contour, Isolines of liquid fraction (fl = 0.98 and 0.07) are plotted

Full size image

Parameter Studies

Effect of arc distribution

The influence of arc distribution on the transport phenomena in VAR is investigated. Of note, spatial and temporal analyses of the location of the arc indicate that the arc does not remain necessarily stable and centric.[11,12,13] For instances, arc rotation along the mid-radius of the electrode, and a linear back-and-forth motion between two regions on the electrode were reported.[11,12,13] To study those unstable movements of the arc, a full-scale 3D model is required.[77] Here, the model assumes a definite distribution of the electric current density into the melt pool. Based on Eqs. [8] through [10], the arc is centric, and the radius of arc is considered as a fraction of the radius of ingot. The distribution of electric current density on the surface of ingot is illustrated in Figure 3(a). The arc conforms to a diffusive mode as the radius of arc increases. The electromagnetic and electric current density fields are shown in Figure 3(b). The intensity of electric current density/magnetic field decreases under the shadow of electrode as the radius of arc increases. As shown Figure 3(b), significant amount of electric current (here assumed 50 pct) crosses the crown at the top of ingot and flows through the mold. In addition, a notable amount of electric current flows through the contact region between mold and ingot. The thermal/solidification and velocity fields are shown in Figure 3(c). The depth of melt pool decreases as the radius of arc increases. These results are in accordance with Zanner et al.’s[65] observations on the impact of arc mode (diffusive/constricted) on the solidification pattern of the ingot. Small radius of arc corresponds to a constricted arc, whereas the large radius of arc mimics the behavior of a diffusive arc. The radiation is large in the vicinity of electrode tip. The central part of the electrode remains relatively cold as a consequence of the large feeding velocity of the electrode (1.15 mm s−1). Globally, the heat transfer is very efficient in the molten pool where a turbulent flow exists. Consequently, the thermal field remains relatively uniform within the molten pool. A vortical flow in clockwise direction is predicted in the molten pool indicating that Lorentz force is stronger than thermal buoyancy. To further clarify this point, the electric current density and Lorentz force fields in the molten pool are illustrated in Figure 3(d). Globally, Lorentz force is directed toward the center except near the contact area where it bends downward. The current density/Lorentz force is stronger for the low radius of arc compared to that for high radius of arc on the central part of the ingot. As a result, the intensity of flow and consequently the depth of molten pool increase as the radius of arc decreases.

Fig. 3
figure 3figure 3

The influence of arc radius (Ri) on transport phenomena where each contour is labeled based on the ratio of the arc radius (Ra) to the ingot radius (Ri). (a) Distribution of current density on the top surface of ingot; (b) Contour of the electromagnetic field including magnetic flux density (left half) and electric current density (right half); (c) Velocity field (left half) and thermal field (right half); (d) Electric current density (left half) and Lorentz force (right half) in the ingot zone. In each contour, Isolines of liquid fraction (fl= 0.98 and 0.07) are plotted

Full size image

Effect of side-arcing

As previously mentioned, significant amount of electric current (30 to 70 pct) crosses the crown and mold lateral wall without entering to the ingot.[23,24] The latter is known as “side-arc” that mostly flows through the crown. Here, the radius of arc is specified (Ra = 0.7 Ri), whereas the amount of side-arcing is changed (30, 50, and 70 pct). The influence of the amount of side-arcing on the electromagnetic field is shown in Figure 4(a). With the increasing amount of side-arcing, the current density intensifies near the edge of electrode. However, the magnetic field becomes weaker near the ingot–mold interface as the amount of side-arcing increases. The interplay between the magnetic field and electric current density determines the strength of Lorentz force in the molten pool that in turn substantially influences the molten pool profile. As illustrated in Figure 4(a), both electric current density, and Lorentz force diminish as the amount of side-arcing increases. As a consequence of variations in Lorentz force field in the ingot zone, as shown in Figure 4(c), the molten pool is tremendously impacted. At a low amount of side-arcing, a clockwise direction of the flow is calculated indicating that the Lorentz force is stronger than buoyancy as illustrated in Figure 4(b). However, a counter-clockwise direction for the flow is predicted considering the large amount of side-arcing (70 pct). For the latter, the buoyancy force becomes more potent. Consequently, the molten pool becomes shorter as the amount of side-arcing increases.

Fig. 4
figure 4figure 4

The influence of the amount of side-arcing on transport phenomena where each contour is labeled based on the ratio of side-arcing current (Is) to the total imposed electric current (It). (a) Contour of the electromagnetic field including magnetic flux density (left half) and electric current density (right half); (b) Velocity field (left half) and thermal field (right half); (c) Electric current density (left half) and Lorentz force (right half) in the ingot zone are shown. In each contour, Isolines of liquid fraction (fl = 0.98 and 0.07) are plotted

Full size image

Effect of gas cooling

The shrinkage (air) gap between ingot and mold has a significant effect on the molten pool profile and subsequently the quality of the final ingot. In the absence of gas cooling by helium or argon, the heat is transferred by radiation in the shrinkage gap region.[89] Introducing a gas of good thermal conductivity such as helium or argon into the gap between the ingot and mold can improve the heat extraction rate, as the heat-transfer mechanism is now due to both radiation and gas conduction.[95] The thermal conductivity of the gas is dependent on both temperature and pressure.[96,97,98] With the increasing temperature, the thermal conductivity of helium drastically increases. The conductivity can reach to that of metal (~ 30 W m−1 K−1) at elevated temperature (~ 700 K).[89] The thermal conductivity of gas remains constant over a large range of pressure. However, the thermal conductivity decreases linearly with the pressure below 1 mm Hg. At moderate pressure (1 to 1000 mm Hg), the thermal conductivity increases with the increase of pressure.[98,99,100] Apparently, a complex relationship exists between the gas pressure/temperature and the thermal conductivity of gas. To explore the relationship, a substantial knowledge in the kinetic theory of gases is required. Here, for the sake of simplicity, we assumed a variable heat-transfer coefficient at the ingot–mold interface to investigate the influence of gas cooling on the transport phenomena at the ingot. Hosamani[89] calculated the overall heat-transfer coefficient (radiation and gas conduction) as a function of gas pressure at various gap widths. He pointed out that the overall heat-transfer coefficient remains nearly constant (below 30 mm Hg) for each gas pressure (2, 6, 10, 20, and 30 mm Hg) and it is independent of gap width (0.1 to 0.0001 mm). The influence of gas cooling on thermal and velocity fields is shown in Figure 5. The radius of arc (Ra = 0.7 Ri) and the amount of side-arcing (50 pct) are identical for all cases. The electromagnetic filed is shown in Figure 2 .Here, only the thermal boundary condition at air gap is different. Figure 5(a) illustrates the field structures when only radiation in the shrinkage gap is taken into account. A heat-transfer coefficient (HTCgas) of 200 W m−2 k−1 is considered in Figure 5(b) that corresponds to a helium gas pressure of 2 mm Hg. In addition, The HTCgas of 500 W m−2 k−1 is used (corresponds to 10 mm Hg of gas pressure) which is equivalent to the specified heat-transfer coefficient at the contact between ingot and mold (Figure 5(c)). As shown in Figure 5, the depth of molten pool decreases as the pressure of cooling gas increases. However, no notable variation in the velocity field (magnitude and direction) is detected. The finding implies that improvement of the heat extraction by gas cooling doesn’t influence the hydrodynamics in the molten pool as long as the flow is driven by Lorentz force.

Fig. 5
figure 5

The influence of gas cooling in the shrinkage area at ingot–mold interface on the flow field (left half) and thermal field (right half). The electromagnetic field for all cases is similar (shown in Fig. 2) considering (Ra = 0.7 Ri) and (Is = 0.5 It). Each case is labeled according to the variation in HTC for gas cooling. In ach contour, Isolines of liquid fraction (fl = 0.98 and 0.07) are plotted. (a) No gas cooling; (b) HTC=200 W m−2 k−1; (c) 500 W m−2 k−1

Full size image

Discussion

Several operational parameters can remarkably impact the pool profile (internal quality) of the final ingot. Those parameters are the power supply, melt rate, gap length, fill ratio (ratio of electrode to ingot diameter), and the pressure of gas cooling in the air gap. Some of those parameters are correlated, while some others are independent. Customarily, empirical rules are applied to select those parameters although these trial-and-error approaches are prohibitively expensive. The trial cost can be significantly minimized by using numerical models such as the one proposed in this work.

The parameters related to the behavior of the arc such as the radius of arc and amount of side-arcing are chosen/determined with our best knowledge within the range of the reported values in the literature. The sensitivity of the modeling results to those parameters is investigated. The predicted pool profile by the model is compared with the experiment, as shown in Figure 6. In the experiment, Nickel particles were used to mark the pool profile.[89] A relatively good agreement is observed for a diffusive arc (Ra = 0.7 Ri) where a notable amount (50 pct) of side-arcing exists. The pool depth is overestimated as both the radius of arc and the amount of side-arcing decrease.

Fig. 6
figure 6

A comparison is made between the experimental result and calculated pool profile using the model considering various arc radius and amount of side-arcing. (a) Calculated pool profile using the model; (b) The marked pool profile is shown that is extracted from Ref. [89] where the marker scale is inserted in the metal macrograph. Ref. [89] is available under Creative Commons By Attribution 4.0 in: https://creativecommons.org/licenses/by/4.0

Full size image

The vacuum plasma region in VAR involves various complex phenomena such as formation and movement of cathode spots at the tip of electrode, the vacuum plasma, side-arcing, the thermal radiation at electrode–mold–ingot interfaces, and the melting of the electrode.

Numerous phenomena considering the melting of electrode and solidification of ingot which are associated with the vacuum arc require further investigation. The evaporation of metal influences the behavior of vacuum arc.[4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101] Numerical models were proposed to investigate the effects of vacuum arc on the melting and solidification of copper.[102,103] It is found that the arc column pressure can influence the depth of molten pool of copper.[104] As previously mentioned, the arc mode (diffusive or constricted) impacts the molten pool depth,[17,105] and consequently the quality of the final ingot.[65] Aiming at predicting the behavior of vacuum arc, it is crucial to explore how cathode spots contribute to the melting of electrode as cathode spots are centers of plasma production.[1,2,3,4,5,6,7,106]

It is believed that the size of electrode and the amount of imposed electric current significantly influence the behavior of cathode spots and consequently, the distribution of arc plasma in the vacuum region.[107,108] The distributions of arc and the self-induced magnetic field are interdependent. Although a dominantly azimuthal magnetic field is assumed in the present study, the magnetic field in the VAR process is indeed three-dimensional.

The models presented (including the one in this paper) to study the vacuum plasma region in vacuum arc remelting (VAR) process are primitive. To make more realistic solidification models of an actual VAR furnace, extensive dedicated efforts are required to model the arc behavior which is the core of VAR process. In spite of the model simplifications and assumptions, which are necessary at the current stage, the proposed model can provide valuable information about the transport phenomena and solidification in the VAR.

Summary

Vacuum arc remelting (VAR) is a secondary metallurgical process used to manufacture ultraclean alloys of steel, and Nickel-based, and Titanium-based alloys. The heat is supplied to a remelting electrode through a DC arc. Numerous phenomena take place in the complex VAR process including formation and movement of cathode spots on the electrode surface, the vacuum arc, the electric current transferred directly between the electrode and mold known as “side-arcing,” the thermal radiation in the vacuum region, magnetohydrodynamics (MHD) in the molten pool, melting of the electrode, and the solidification of the ingot. First, modeling challenges related to the aforementioned phenomena are briefly described. Second, a robust and computationally feasible model is proposed to get better insight into VAR. The electromagnetic field is calculated in the entire process including the electrode, vacuum, ingot, and mold. The influence of magnetic field on flow through Lorentz force in the molten pool is taken into account. Calculation of the heat radiation in the vacuum region is carried out. The thermal field in the whole process is computed. In addition, the solidification of a Titanium-based alloy (Ti-6Al-4V) and the formation of the molten pool are calculated.

The influences of three important parameters on the behavior of VAR are addressed. Modeling results considering the mode of arc (diffusive or constricted) by variation in the radius of arc, the amount of side-arcing, and the gas cooling in the shrinkage gap between ingot and mold are quantitatively analyzed. The molten pool depth increases as the radius of arc decreases. With the increasing amount of side-arcing, the molten pool depth decreases. Furthermore, gas cooling enables us to fairly improve the internal quality of ingot (shallow pool depth) without affecting hydrodynamics in the molten pool. Results regarding the molten pool profile are validated against an experiment.