Size Distribution of Graphite Nodules in Hypereutectic Cast Irons of Varying Nodularity

Abstract

An SGI was machined into 400 g cylindrical pieces and remelted in an electrical resistance furnace protected by Ar gas to produce materials ranging from SGI to CGI. The graphite morphology was controlled by varying the holding time at 1723 K (1450 °C) between 10 and 60 minutes. The discrete sectional size distribution of nodules by number density was measured on cross sections of the specimens and translated to volumetric distribution by volume fraction. Subpopulations of nodules were distinguished by fitting Gaussian distribution functions to the measured distribution. Primary and eutectic graphite, were found to account for most of the volume of nodular graphite in all cases. For holding times of 40 minutes and greater, corresponding to nodularity roughly below 40 pct, the primary subpopulation was very small and difficult to distinguish, leaving eutectic nodules as the dominant subpopulation. The mode and standard deviation of the two subpopulations were roughly independent of nodularity. Moreover, the nodular and vermicular graphite were segregated in the microstructure. In conclusion, the results suggest that the parallel development of the vermicular eutectic had small influence on the size distribution of eutectic graphite nodules.

Introduction

Production of compacted graphite iron (CGI) requires careful process control due to a narrow production window. Despite the difficulties associated with the production of CGI, the material has become common in automotive components like engine blocks, cylinder heads, and is also used in exhaust manifolds and bedplates. It is an achievement to be able to cast complex shapes in CGI, however, this often comes with increased losses from defective castings. The failure in designing and producing sound CGI components is attributed to inadequate solidification models for the material, which leaves designers and foundry engineers with unsatisfying tools.[1]

The primary difficulty relates to the control of the graphite shape. Although the vermicular graphite morphology is the most widely associated with CGI, it is not feasible today to consistently produce cast irons with 100 pct vermicular graphite. ISO 16112:2017 uses a quantity called nodularity which is a measure of how much of the graphite has a spheroidal shape.[2] The standard holds that flake graphite is not tolerated in CGI due to its deleterious effect on mechanical properties, however, a nodularity of up to 20 pct is tolerated. With higher nodularity, the material solidifies more like SGI, which is known for its increased tendency for feeding related defects. Nevertheless, most research on CGI is directed towards vermicular graphite alone, leading to a lack of understanding about the role of the nodular graphite and its interaction with the vermicular graphite.

A number of authors have identified subpopulations of graphite nodules distinguished by characteristics like size, segregation patterns, and location in the microstructure.[3,4] The phenomenon of subpopulations of graphite nodules is known from SGI where they are typically reflected in the discrete size distribution of nodules.[5,6,7,8,9] A subpopulation of larger nodules can typically be found in eutectic and hypereutectic SGI and has been ascribed to primary precipitation of graphite.[5] It has on the other hand been reported that bimodal distribution was found in cast irons with a carbon equivalent as low as 4.1 wt pct but not in cast irons with 4.4 wt pct.[9] Fine nodules, believed to have formed during a late stage of solidification have been reported for a wide range of cooling conditions in SGI[7,10,11,12] and CGI.[4] A subpopulation of small nodules located in last to freeze regions have been reported for SGI quenched from a partially solid state, indicating that they are promoted by rapid cooling.[10] However, other studies indicate that a third population of small nodules is promoted by slow cooling, in thicker plate castings.[7,9] Similarly, smaller subpopulations of lamellar graphite-austenite eutectic cells have been observed in lamellar graphite irons (LGI).[11,13–16] These have been associated with both expansion penetration[15] and shrinkage defects.[4] The smaller subpopulation of eutectic cells in LGI has been attributed to a late spike in undercooling associated with impingement of the prior eutectic cells.[13] As cells impinge, growth is restricted, leading to a drop in the rate of internally generated heat while heat extraction continues. Consequently, the temperature of the casting drops, leading to increased undercooling. When undercooling exceeds the prior maximum, additional heterogeneous nucleation sites may be activated. The phenomenon has been reproduced using numerical simulation of solidification, where the influence of grain impingement and microsegregation was modeled.[14]

A combination of the magnitude of undercooling in the late part of solidification and segregation of residual Mg has been proposed to explain why the late nucleation of graphite results in nodules rather than vermicular shape in CGI.[3] The development of nodules in CGI has not been studied closely. This paper investigates the evolution of the size distribution of graphite nodules in cast irons with graphite morphology ranging from SGI to CGI.

Material

In order to vary the nodularity over the range between SGI and CGI while holding other parameters as constant as possible, a single SGI was remelted in an Ar atmosphere as detailed in a recent publication.[18] The nodularity was controlled by varying the holding time applied in the remelting process. Early attempts to produce CGI from SGI through remelting typically resulted in some fraction of lamellar graphite. The target residual Mg in the melt was therefore set higher for the present alloy, with the intent of delaying the deterioration into lamellar graphite. Since the material analyzed in this work was remelted and solidified in the laboratory, the focus of the methodology description is on the remelting procedure. The initial casting procedure is briefly described here. An Fe-Si-Mg nodularizer was introduced using the tundish ladle method. Fe-Si inoculant was introduced in-stream during pouring. The chemical composition shown in Table I was measured using spark emission spectrometer on a rapidly solidified coin sample produced seconds before pouring. The base alloy was cast in two sand molds, produced using a 3D sand printer with furan binder. The mold design featured open cylindrical cavities Ø50 mm. A gating system distributed the melt from the pouring box to the cylinders, filling them from the bottom. The two molds were poured in sequence over the course of less than two minutes. In preparation for the experiments, the gating system was removed and smaller Ø38 mm cylinders were machined using a lathe. The length was adjusted such that the final weight was 400 ± 0.5 g, approximately 50 mm.

Table I Chemical Composition of the Base Alloy Given in Weight Percent

Experimental Setup

The experimental setup is based on an earlier setup[17] with minor modifications. The same setup was also used in a recent publication.[18] A schematic of the setup is available in Figure 1. The length of the central ceramic pipe is 900 mm. The lids of the pipe are not water cooled as in the referenced publication.[17] Ar with a minimum purity of 99.999 vol. pct is introduced at a rate of 5 l/min from the bottom of the chamber. Excess gases escape through a hole in the top lid. The machined material specimens are placed in alumina crucibles with an inner diameter of Ø40.6±0.6 mm and positioned in the middle of the furnace, resting on a column of graphite. S-type thermocouples are protected by quartz glass tubes, which were sealed in the bottom end using an oxy-fuel torch. At room temperature, the glass tubes were inserted through holes in the top lid of the furnace to a depth of 20 mm over the bottom of the crucible, one in the center, a second against the inside of the crucible wall, and a third against the outside of the crucible as indicated in Figure 1. The correct height was marked by placing O-rings on the tubes against the lid. Tubes and thermocouples were raised 200 mm above the target position to avoid unnecessary exposure to high temperatures. The furnace temperature, controlled with respect to a thermocouple just outside the ceramic pipe, was ramped up from room temperature to 1723 K (1450 °C) over 75 minutes followed by a holding time of 10 to 60 minutes according to Table II. During the ramp-up, the metal melted and filled out the lower part of the crucible. 5 to 10 minutes before the end of the holding time, quartz tubes and thermocouples were lowered into the correct position as previously marked with O-rings. After the holding time, the furnace was turned off with the specimen left inside to cool. The feeding of Ar into the chamber was discontinued after the temperature had reached below 1273 K (1000 °C). The experiments were carried out in a randomized order. Following the experiments, the solidified specimens were cut at an approximate height of 20 mm, and the Ø40.6±0.6 mm surface of the bottom half was mounted in bakelite with carbon filler. Despite the additions of Cu and Sn, considerable amounts of ferrite were found in conjunction with graphite in all specimens, making preparation for microscopy more difficult due to smearing of ferrite over the graphite. The cut surface was prepared by manual mechanical grinding from a grit size of P80 (FEPA) down to P2000 (FEPA), followed by automated polishing with 3 µm diamond suspension polishing on a napless surface and a final step of manual polishing with an oxide slurry.

Fig. 1

A schematic of the experimental setup. Adapted from Ref. [17]

Table II Overview of the Experimental Series

Analysis

Size Distribution of Graphite Nodules

To estimate the size distribution of the nodular graphite, the particle areas A and maximum Feret diameter l_max were measured on the cross sections of the specimens using digital microscopy and a commercial image analysis software.

Micrographs were captured using an objective lens magnification of 5× and a camera adapter magnification of 0.63×, producing a pixel side length of 1.081 μm. This is approximately double the pixel size compared to an investigation of SGI,[7] however, it appears reasonable considering that the nodules in this case are larger. A minimum of 40 non-overlapping micrographs were captured row-wise by offsetting each micrograph a quasi-random distance from the previous. Areas containing porosities were rejected. Together the micrographs added up to an area of at least 151 mm² for individual specimens or at least 531 mm² for specimens treated with a single holding time.

To isolate nodular graphite, only particles fulfilling certain criteria were included in the analysis.

The first criterion is that the full cross section of the particle must be visible in the micrograph, excluding all particles in contact with the boundary of the micrograph. This was handled using the image analysis software.

The second criterion is l_max > 10 μm. The reason behind this is that preliminary microscopy showed that particles within this size range were typically identified as microporosities, slag particles, and surface defects introduced during sample preparation. This is in agreement with comparison between image analysis and automatic counting using scanning electron microscope and energy-dispersive spectrometry.[8,19]

The third criterion aims to exclude graphite particles which are not spherical. Roundness was calculated in line with ISO 16112:2017[2] as the area of the particle A divided by the area of a circle A_circle with a diameter equal to the maximum Feret diameter l_max, i.e.,

$$ {\text{Roundness}} = \frac{A}{{A_{\text{circle}} }} = \frac{4}{\pi } \cdot \frac{A}{{l_{\hbox{max} }^{2} }}. $$

(1)

Only particles with Roundness > 0.525 were included in the graphite nodule size distribution analysis. The value 0.525 corresponds to the lower limit of roundness considered in the calculation of percent nodularity according to ISO 16112:2017.

Since the roundness of the considered particles varied, the basis of the size distribution is the diameter corresponding to a circle with the same area A as the particle, which is referred to as the equivalent diameter

$$ d_{\text{A}} = 2\sqrt {A/\pi } . $$

(2)

A size distribution can now be obtained by sorting the particles into a number of size classes and then counting the number of particles within each group. The sectional size distribution is however deceiving, as the circular diameter of a spherical particle which appear on a cross section depends not only on the size of the particle, but also on where it is sectioned. The volumetric size distribution can be estimated using statistical methods. In this paper, a finite difference method based on continuous size distribution is employed for this purpose.[20] According to this method, the size classes of a population have a common width Δd defined by

$$ \Updelta d = d_{\text{A}}^{ \hbox{max} } /k, $$

(3)

where d ^max_A is the largest equivalent diameter in the considered population and k is the number of size classes. A particle is considered to be inside class j if its equivalent diameter $d_{\text{A}} > d_{j} - \Updelta d/2,$ and $d_{\text{A}} \le d_{j} + \Updelta d/2,$ where d_j is the central diameter between the boundaries of the jth class. The sectional size distribution expressed in terms of number density N ^j_A is now obtained by counting the number of particles within each class and then dividing by the total surface area from which the particle data were obtained, A_tot,

$$ N_{\text{A}}^{j} = N_{j} /A_{\text{tot}} $$

(4)

The volumetric size distribution is then estimated from the sectional size distribution using

$$ N_{\text{V}}^{j} = \frac{1}{\Updelta d}\left( {B(j,j)N_{\text{A}}^{j} + \sum \limits_{i = j}^{k} B(i,j)N_{\text{A}}^{i} } \right). $$

(5)

For calculation of the coefficients B(j,j) and B(i,j), and more details regarding the calculation of N ^j _i , the reader is referred to the original description of the finite difference method.[20]

It has been reported that conversion of the volumetric number density N ^j_V to volume fraction V ^j_V results in a more Gaussian-like distribution.[20] Since this facilitates analysis, the size distribution is primarily expressed as V ^j_V in this paper. V ^j_V is calculated by multiplying N ^j_V by the mean particle volume within the size class. Assuming a uniform distribution of diameters of the particles in the size class, the mean volume can be calculated by integration of the volume over the size class, followed by division by the width of the size class.

$$ V_{\rm V}^{j} = \frac{{N_{v}^{j} }}{\Updelta d} \int \limits_{{d_{j} - \Updelta d/2}}^{{d_{j} + \Updelta d/2}} \frac{4\pi }{3}\left( {\frac{x}{2}} \right)^{3} dx = \frac{{N_{\rm V}^{j} }}{\Updelta d}\, {\ast}\, \frac{\pi }{24}\, {\ast}\,\left[ {\left( {d_{j} + \frac{\Updelta d}{2}} \right)^{4} - \left( {d_{j} - \frac{\Updelta d}{2}} \right)^{4} } \right] $$

(6)

Since the distribution of spheroidal graphite often features multiple modes associated with separate nucleation events, it is beneficial to approximate the subpopulations making up the measured distribution. To do this, V ^j_V is approximated as a sum of a number of subpopulations assumed to have Gaussian distributions. The approximation $V_{\rm V}^{j\ast}$ is expressed as

$$ V_{\rm V}^{j\ast} = \mathop \sum \limits_{s = 1}^{n} \left\{ {\mathop \smallint \limits_{{d_{j} - \frac{\Updelta d}{2}}}^{{d_{j} + \frac{\Updelta d}{2}}} v_{\rm s}^{\ast} (x| \mu_{\rm s} ,\sigma_{\rm s} ,A_{\rm s} )dx} \right\}, $$

(7)

where n is the number of subpopulations comprising $V_{\rm V}^{j\ast}$, the subscript s is an integer denoting the subpopulation, x is the particle diameter, μ_s, σ_s, and A_s are the mean, standard deviation, and scaling factor of subpopulation $v_{\rm s}^{\ast}$. The subpopulation $v_{\rm s}^{\ast}$ is composed of a Gaussian probability density function p_s scaled by a factor A_s

$$ v_{\rm s}^{\ast} (x | \mu_{\rm s} ,\sigma_{\rm s} ,A_{\rm s} ) = A_{\rm s} p_{\rm s} \left( {x | \mu_{\rm s} ,\sigma_{\rm s} } \right) $$

(8)

By combining [7] and [8] $V_{\rm V}^{\ast} \left( {x_{i} } \right)$ can be expressed as

$$ V_{\rm V}^{\ast} = \mathop \sum \limits_{s = 1}^{n} A_{\rm s} \left\{ {P_{\rm s} \left( {d_{j} + \frac{\Updelta d}{2} | \mu_{\rm s} ,\sigma_{\rm s} } \right) - P_{\rm s} \left( {d_{j} - \frac{\Updelta d}{2} | \mu_{\rm s} ,\sigma_{\rm s} } \right)} \right\}, $$

(9)

where $P_{\rm s} (x | \mu_{\rm s} ,\sigma_{\rm s} )$ is the cumulative distribution function of $p_{\rm s} \left( {x | \mu_{\rm s} ,\sigma_{\rm s} } \right)$

$$ P_{\rm s} (x | \mu_{\rm s} ,\sigma_{\rm s} ) = \mathop \smallint \limits_{ - \infty }^{x} p_{\rm s} \left( {x | \mu_{\rm s} ,\sigma_{\rm s} } \right)dx $$

(10)

Conveniently, since $P_{j} \left( {\infty | \mu_{\rm s} ,\sigma_{\rm s} } \right) = 1,$ the scaling factor A_s is the total volume fraction of approximated subpopulation $v_{\rm s}^{\ast}$. The parameters μ_s, σ_s, and A_n are unknown, but can be estimated by fitting $V_{\rm V}^{j\ast}$ to $V_{\rm V}^{j}$. The fitting was performed by minimization of the sum of absolute error $\sum\nolimits_{j = 1}^{k} {{\text{abs}}(V_{\rm V}^{j\ast} - V_{\rm V}^{j} )}$ for the parameters A_s, μ_s, and σ_s. Gradient minimization methods were found not to be suitable because of their tendency to converge towards local minima near the starting point. The minimization was instead performed using a simple algorithm which randomly explores an incrementally smaller variable space around a number of best performing candidates of the last iteration, until a satisfying fit had been found. The starting values for the minimization were chosen intuitively based on the shape of the distribution.

Selective Tinting

Selective Tinting was applied to get a qualitative overview of the solidification structure of the specimens. A selective tinting reagent with the formula 10 g NaOH, 40 g KOH, 10 g Picric acid, and 50 mL distilled H₂O has been proven useful for cast iron metallography as it forms a thin oxide film with a thickness depending on the local silicon concentration.[21] Since the silicon partitions into the austenite during solidification and is gradually exhausted from the liquid, the color patterns caused by thin-film interference correlates to some degree with the solidification chronology of the matrix. After a proper treatment with the reagent, the color of the pearlite matrix typically ranges from pale yellow or white to bright blue, corresponding to the lowest and highest concentration of Si, or the earliest and latest solidified areas, respectively.

After graphite measurements were completed, the mounted specimens were partially submerged face-down in the reagent which had been heated to 367.15 K (94 °C). An initial treatment of 8 minutes was performed. The specimen was then washed, dried, and examined under an optical microscope. If needed, the specimen was incrementally reintroduced to the solution for shorter durations until the tinting was judged to be adequate.

The full-treated surface was captured digitally using an optical microscope at 2.5× objective lens magnification and the images were stitched into panorama micrographs using the software Image Composite Editor. More details regarding the tinting procedure and the interpretation of the resulting patterns are available elsewhere.[22]

Result and Discussion

To support the discussion of the results, equilibrium calculations were performed for the composition listed in Table I using Thermo-Calc Software[23] with the TCFE7 databank. Sn was excluded because it is not included in TCFE7. The Fe-C section of the equilibrium phase diagram is shown in Figure 2. The results of the calculations are referred to collectively as “EQ” in the text.

Fig. 2

Fe-C section of the equilibrium phase diagram for EQ

Graphite Measurements

As described earlier, the purpose of varying the holding time was to control the proportions of nodular and vermicular graphite. The reason for this effect appears to be the fading of the Mg treatment, as was shown in a recent paper which was partially based on the same experiments.[18]

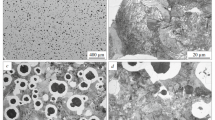
The transition from SGI to CGI is illustrated in Figure 3 using examples of micrographs used for graphite characterization. The percent nodularity displayed in Figure 4 measured according to ISO 16112:2017 suggests that the nodularity drops roughly in proportion to holding time. A linear least squares fit indicates that nodularity drops by about 1.5 pct every minute, however, this seems to be specific to this particular experimental setup as other researchers have reported a transition from SGI to LGI within a few minutes.[24]

Fig. 3

Selected micrographs illustrating the change from nodular iron to compacted graphite iron with increasing holding time. (a) H10, (b) H20, (c) H30, (d) H40, (e) H50, (f) H60

Fig. 4

Nodularity (ISO 16112:2017) as a function of holding time. Round markers represent the sample means. Whiskers represent the 95 pct confidence intervals for the means of the individual specimens

The measured area fraction of graphite is an indicator of the quality of the preparation of the cross section and the graphite measurements as it is expected to fall close to theoretical values for the alloy. The lever rule applied to Figure 2 and conversion from mass to volume fraction using densities provided by EQ, suggests a graphite fraction between 10.1 pct for a pearlitic matrix and 11.9 pct for a ferritic matrix. The specimens featured a predominantly pearlitic matrix, but some ferrite was found in all specimens in conjunction with graphite. Figure 2 shows that the means for the specimens exposed to the same holding times are in the neighborhood of the theoretical range, but not strictly inside it. It also indicates that the mean graphite fraction for H50 is significantly higher than H10 and H20. Consequently, if a line was to be drawn through the confidence intervals in the graph, it must have a positive slope. It is possible that this trend relates partly to an increase in ferrite content, however the ferrite content was not measured in this study. Figures 4 and 5 are good indicators of the validity of the graphite data on which the size distribution analysis is based.

Fig. 5

The area fraction of graphite (ASTM A247) for each specimen as a function of holding time. Round markers represent the means of the specimens exposed to equal holding time. Whiskers represent the 95 pct confidence interval for the mean. The dashed lines indicate the theoretical volume fraction graphite for the alloy calculated using the lever rule for fully ferritic and fully pearlitic matrix

Cooling Curves

Before the cooling curves are interpreted, some matters regarding the experiment and temperature measurements are best discussed.

It was the intention of the authors to vary the nodularity while keeping all other variables as constant as possible. Unfortunately, reviewing the cooling curves of Figure 6, it is observed that the maximum temperature is lower for H10 and that there is a relationship between holding time and cooling rate. The primary reason for the lower maximum temperature of H10 is that the programmable furnace controls the temperature using feedback from a thermocouple located outside the ceramic pipe. For this reason, the temperature inside the specimen lags behind the furnace temperature during heating. The lag is also aggravated by the thermal arrest of the specimen during melting. Once the furnace temperature reaches the target holding temperature, the equilibration of the temperature in the specimen with its environment is slow since the temperature difference which drives heat extraction progressively decreases. After the holding time of 10 minutes for H10, the temperature of the molten specimen had not yet caught up with the furnace air temperature. Moreover, the temperature in the specimen appears to stabilize at values below that of the furnace target temperature. This is, again, a consequence of the furnace being controlled using feedback from a thermocouple located outside the ceramic pipe.

Fig. 6

The measured central temperature of all specimens from the time the furnace was turned off. T_G denotes the equilibrium graphite liquidus temperature. T_E denotes the equilibrium eutectic temperature. The curves are smoothed using a moving average operation

Similarly, the reason for the slight dependence of the cooling rate on the holding time is likely that the materials surrounding the heated chamber continue to absorb heat during the holding time, even after the target temperature is reached. The greater heat content of the system after longer holding time then takes more time to dissipate. The influence of holding time on cooling rate appears to be negligible for holding times of at least 40 minutes, so this appears to be the time required for the process to stabilize.

Figure 7 shows the rate of temperature change over the solidification range. The curves which are drawn with dotted lines display oscillations for temperatures above the eutectic arrest. These oscillations are considered to be disturbances in the measurement and are unlikely to relate to any phase transformations. A potential source could be movement of the melt due to thermal convection. Analysis of the early developments of the cooling curves is therefore limited to the solid lines, which appear to lack these disturbances.

Fig. 7

Rate of temperature change as a function of temperature for the central thermocouple. The curves are grouped by holding time and each group is offset by 0.1 °C/s from the neighboring group with lower holding time to facilitate distinction. Unlike the solid curves, the dotted curves display temperature disturbances, particularly for temperatures leading up to the eutectic arrest. Curves are smoothed using a moving average operation

Aside from these unintended effects, the curves also provide clues about the solidification characteristics of the materials. H10 stands out relative to cooling curves for longer holding times. First of all, Figure 7 indicates a slight but reproducible drop in the cooling rate (T1) for H10 around 1433 K (1160 °C). A comparison to Figure 8 shows that this occurs well above maximum temperature during eutectic arrest, which is around 1420 K (1147 °C). Considering the hypereutectic composition of the alloy, this leads to the interpretation that reduction of slope at T1 is likely caused by precipitation of graphite. Hypereutectic SGI with carbon equivalents over 4.6 are reported to typically feature a proeutectic reaction strong enough to produce a brief recalescence on the cooling curve followed by a reduced slope.[25] The reason only a reduced slope is recognized in the present case may relate to the poor conditions for nucleation of graphite. Results of more recent research also suggest that the hypereutectic reaction is more easily recognized under slow cooling conditions, or may be obscured by rapid cooling.[26]

Fig. 8

A closer look at the cooling curves in Fig. 6. The time of H10 begins when the furnace was turned off. Each of the remainder groups is offset 7 min from the preceding group to facilitate distinction. T_E denotes the equilibrium eutectic temperature. The curves are smoothed using a moving average operation

Figure 8 also shows that H10 and one of the repetitions of H20 are characterized by two local maxima during eutectic arrest. This is also typical for hypereutectic SGI.[25] The first maximum is often referred to as an initiation stage of the eutectic reaction and is associated with dendritic growth of austenite.[27] In certain cases, researchers have attributed a change of slope prior to the eutectic arrest as the initiation stage of the eutectic reaction; however, in these cases there was no sign of an initiation stage during the latter arrest.[11] This has by others been described as merging of the primary graphite reaction and the initiation stage of the eutectic reaction, common for hypereutectic SGI with carbon equivalent below 4.6.[25] However, in the present case, the reduction in the slope and the first maximum during eutectic arrest are roughly 2 minutes and 13 K apart and not merged. The reaction denoted T1 in Figures 7 and 8 is for this reason regarded as precipitation of primary graphite, while the first maximum during eutectic arrest is regarded as the initiation stage of the eutectic reaction.

Studying Figure 7 further, a reaction comparable to T1 for H10 is difficult to recognize among the remaining cooling curves. However, considering only the curves drawn with solid lines, which appear to lack the oscillatory temperature disturbances, a small reaction (T1) seams to appear for H30 at a lower temperature around 1425 K (1152 °C). Moreover, looking at the solid curve for H50, no such reaction is distinguished. This is an indication that the primary graphite gradually disappears as longer holding time is applied. A plausible explanation would be the dissolution of suitable substrates for graphite to nucleate on, a process often referred to as fading.[28] In the present case, no inoculants were added after the material had been remelted in the laboratory furnace. However, it appears possible that some residual substrates were still present in the melt after the shortest holding time of 10 minutes. It has for example been observed that it can take minutes for spheroidal graphite to completely dissolve after the material has melted.[29,30]

The initiation stage of the eutectic reaction no longer appears for longer holding times, indicating dendritic growth of austenite did not occur in these materials. However, selective tinting revealed that all specimens contained a substantial amount of dendritic structure, as indicated by Figure 9. The dendritic structure is recognized by its regular pattern of parallel and orthogonal arms colored bright blue indicating a high silicon content and therefore an early crystallization. The question is then why majority of curves only display a single maximum temperature during the eutectic arrest. A plausible explanation for this discrepancy is that the first stage of the eutectic is only easily distinguished from the latter stage on cooling curves when the latter is considerably slower than the first. When the nodularity is high, solidification slows down notably after the first stage due to the envelopment of most graphite by austenite. This slows down the rate of solidification leading to increased undercooling which causes activation of additional nucleation sites for graphite. A second stage of recalescence occurs when the number of graphite particles are high enough to compensate for the restrained growth rate. The relatively high growth rate of the vermicular eutectic, on the other hand, leads to a more seamless transition between the stages, making them difficult to distinguish on the cooling curves.

Fig. 9

The cross sections on which graphite measurements were made, tinted with Motz[21] picric solution. The micrographs extend from the periphery of the specimen on the left hand side, to the approximate center of the specimen on the right-hand side. One of the repetitions for each condition is shown, (a) H10, (b) H20, (c) H30, (d) H40, (e) H50, (f) H60. The black spots on the right-hand side are porosities. The peripheral layer indicated at the bottom of the micrograph displays larger vermicular eutectic cells than further away from the surface (Color figure online)

Another trend among the cooling curves, not yet discussed, is the temperature at maximum undercooling, denoted T2 in Figure 8, which is defined as the minimum temperature before recalescence. These values are also plotted as a function of the measured nodularity in Figure 10, where they form a valley between H10 and H60. Two factors which likely contribute to this trend are found by looking at the extrema of H10 and H60. The early reaction which likely relates to precipitation of primary graphite was particularly prominent in H10. It has been shown that austenite nucleates relatively easily on graphite.[31] It therefore appears reasonable that the high temperature at maximum undercooling in H10 relates to nucleation of austenite being facilitated by the presence of primary graphite particles. With increasing holding time, primary graphite particles became rarer, impeding the nucleation of austenite. This factor does not explain the relatively high temperature at maximum undercooling for H60. Instead this is more likely related to the higher growth velocity of vermicular graphite–austenite eutectic cells compared to nodules enveloped by shells of austenite. This is in agreement with the observation that the temperature of maximum undercooling appears less scattered as a function of percent nodularity than as a function of holding time as can be seen in Figure 10.

Fig. 10

Temperature at maximum undercooling (the local minimum temperature before recalescence) as a function of percent nodularity. In the cases where there were two local minima, the lower temperature is displayed. Whiskers represent the 95 pct confidence interval for the means

An alternative explanation for the observed patterns on the cooling curves is decarburization. This would cause the graphite liquidus to drop, which could explain the gradual disappearance of the primary graphite reaction with increasing holding time. The equilibrium temperature between austenite and liquid would then rise, which could explain the observed increase of the temperature at maximum undercooling prior to the eutectic reaction for H60. Decarburization of this magnitude is however considered unlikely, not only because of the continuous flow of argon into the furnace during the experiment. A shift from the initial hypereutectic carbon content of 3.86 wt pct C to the eutectic point at 3.53 wt pct C according to Figure 2, would cause the volume fraction graphite to drop by about 1 pct according to the lever rule. Figure 5 indicates the contrary, a small but significant increase in area fraction graphite with increasing holding time. Considering the theoretical limits of 100 pct ferritic and 100 pct pearlitic matrix presented in the graph, it is conceivable that such a decrease could be obscured by a parallel increase in volume fraction ferrite. For an increase in ferrite content to counterbalance such a drop, the ferrite fraction of the matrix would have to increase by 58 pct. To also produce the measured increase in Figure 5, the required increase would have to be even larger. While the ferrite content was not measured in this study, it was clear from the color-etched micrographs that an increase of this magnitude did not occur. An outlier is one of the specimens in H60, visible in Figure 9. This specimen appears to contain roughly 50 pct ferrite. However, the remaining specimens were predominantly pearlitic. For these reasons, it appears more likely that the observed trends in the cooling curves relate mainly to a fading nucleation potential for graphite and a change from spheroidal to vermicular graphite.

Graphite Nodule Size Distribution

The size distribution of graphite nodules was investigated for all specimens. To facilitate interpretation of the results, certain aspects of the analysis and how it is presented is first clarified.

The graphite particle data are lumped into populations by holding time and is referred to by the aliases introduced in Table II. The graphite particle populations are expressed as number density by volume N_V in Figure 11 and volume fraction V_V in Figure 12. The conversion to volumetric size distribution tends to amplify features of the sectional distribution, causing considerable noise if the resolution is too high. 20 size classes were in this work found to be an appropriate balance between resolution and noise. Note that while the number of size classes are the same for all populations, the size class width varies since it depends on the population’s maximum diameter as required by the applied method for conversion to volumetric number density. The mid-point and height of each size class are represented by markers connected by lines to facilitate comparison.

Fig. 11

Size distribution of volumetric number density of graphite nodules for H10 through H60. Markers are placed at the central point of respective size class on the horizontal axis

Fig. 12

Size distribution of volume fraction of graphite nodules for H10 through H60. Markers are placed at the central point of respective size class on the horizontal axis

Now that the background of the data presented in Figures 11 and 12 is being clarified, the changes of the distributions as a function of holding time can be examined.

The total number density and volume fraction of graphite nodules decrease with increasing holding time. This is according to expectation as the graphite content is roughly constant while the nodularity drops with increasing holding time as is shown in Figures 4 and 5.

The volumetric number density N_V is large for small diameters, however, these particles make up a small volume. Likewise, the largest nodules may make up a relatively large volume but are on the other hand few.

All V_V displayed negative values for the smallest size group. This is caused by a combination of the imposed particle filter l_max > 10 μm and the conversion from sectional to volumetric distribution. The filter reduces the number density within this group below what is expected if the groups of larger spheres were randomly sectioned.

Figures 11 and 12 both indicate that the distributions are not unimodal, but the large overlap of the subpopulations makes it difficult to estimate the relative sizes. To find out more about the subpopulations that constitute the distribution, further treatment of the data was necessary. This is the topic of the next section.

Distinction of Subpopulations

The size distribution has been reported to more closely resemble Gaussian distribution when expressed in terms of volume fraction rather than number density.[20] This appears to be true also in this work, which motivates the choice of Gaussian distribution for the approximation of subpopulations. The subpopulations are denoted $v_{n}^{\ast}$ in accordance with Eq. [7]. A number of five subpopulations were considered sufficient to address the main features of V_V. The parameters describing the subpopulations obtained from the fitting of $V_{\rm V}^{\ast}$ to V_V are found in Table III.

Table III Parameters of the Estimated Subpopulations, Obtained by Fitting to the Graphite Data

A comparison between V_V and $V_{\rm V}^{\ast}$ is shown in Figure 13. The approximation was more easily fitted to graphite data with higher nodularity. This may be explained by the shrinking sample size and increasing amount of vermicular graphite being mistaken for nodules.

Fig. 13

Comparison between the measured size distributions V_V and the approximated size distributions $V_{\text{V}}^{\ast}$ including its subpopulations $V_{n}^{\ast}$ where the subscript n denotes the index of the subpopulation. The ticks on the x-axes represent the size class edges while the markers are located at the mid-points of associated groups. E_abs denotes the sum of absolute errors between the measured and the approximated distribution. (a) H10, (b) H20, (c) H30, (d) H40, (e) H50, (f) H60

An important question is whether the distributions are really composed of five subpopulations of graphite, or whether the smaller subpopulations are rather compensating for discrepancies in the fit. It would of course be possible to describe any discrete distribution perfectly if only the number of subpopulations were the same as the number of size classes. As stated earlier, a number of five subpopulations were regarded necessary to address all main features which appeared on the curve.

Reproducibility of a subpopulation can be considered higher if a subpopulation of similar characteristics appears in independent cases. As shown in Figure 14 subpopulation $v_{3}^{\ast}$ has a wide and stable standard deviation while being located around roughly the same mode for all holding times. $v_{4}^{\ast}$ appears consistent as well for H10 through H30 but shrinks to a size where it is difficult to recognize for longer holding times. It appears that at the very least, these two subpopulations relate to actual subpopulations of graphite nodules related to solidification phenomena.

Fig. 14

Means (modes) of the approximated subpopulations as a function of holding time. Whiskers indicate the standard deviation of the subpopulations. Subpopulations are denoted by numbers 1 to 5

$v_{5}^{\ast}$ is however regarded as statistical error rather than being a physical subpopulation. The rather sporadic features on the far right of the distribution is understandable considering that a small number of nodules translates to a substantial volume fraction in this size range.

Subpopulations $v_{1}^{\ast}$and $v_{2}^{\ast}$ describe the smaller particles which are influenced by the criterion $l_{\rm max} > 10\,\mu\text{m}$ and polluted by some unwelcome features in the micrographs. The separation of the smaller nodules into two subpopulations $v_{1}^{\ast}$and $v_{2}^{\ast}$ was motivated by the peak near 30 µm which is most pronounced in H50 and H60. Figure 15 illustrates that as nodularity drops, $v_{1}^{\ast}$ is polluted by mischaracterized vermicular graphite. Moreover, Figure 15 indicates that $v_{2}^{\ast}$ is primarily populated by nodular graphite and is not easily confused with vermicular graphite. Note however that sections of nodules can appear smaller than the actual size of the spherical particle. The color coding is also mutually exclusive, in contrast to the considerable overlap of subpopulations in Figure 13. It is for this reason difficult to link the particles seen in Figure 15 to any $v_{n}^{\ast}$ with certainty, and this is true especially smaller particles.

Fig. 15

Nodule sections have been divided into size ranges. (a, b) H10, (c, d) H60. Size ranges are given within brackets in the figure, with arrows pointing to examples of nodules within the range. In the online version of this paper, the classes are also distinguished by color (Color figure online)

Primary Graphite Nodules

Solidification of hypereutectic SGI is expected to begin with the formation of graphite, if conditions for nucleation are adequate. If the conditions are right, this can be observed in the form of floatation, leading to graphite floating towards the surface of the melt.[32] The particles grow spherically at a rate delimited by diffusion of carbon from the liquid to the graphite.[5] The growing graphite gradually consumes carbon from the melt as the temperature drops. Since the primary graphite has more time to grow and initially at a higher rate, it is expected to form a set of larger graphite particles. For this reason, $v_{4}^{\ast}$ and $v_{5}^{\ast}$ likely correspond to primary graphite. According to Table III, the two populations combined make up a volume fraction of 4.7 pct in H10 which accounts for almost half of the total graphite content. However, as EQ suggests an equilibrium volume fraction of graphite of about 1 pct just above the eutectic temperature, most of the carbon was added to these graphite particles below the eutectic temperature.

It has been proposed that the solidification of CGI begins, similar to SGI, with nodules growing suspended in the melt.[33] Upon interaction with austenite, nodules are either enveloped by the austenite completely and continue to grow spherically or degenerate into vermicular growth depending on the conditions in the melt. Figure 16 shows that as holding time increases, the volume fraction of $v_{4}^{\ast}$ decreases sharply from H10 through H30. By H40 $v_{4}^{\ast}$ and $v_{5}^{\ast}$ are so small that they may as well be noise. Considering the gradual disappearance of the primary graphite reaction discussed earlier in relation to Figure 7, this appears to not only reflect a reduction of spheroidal primary graphite, but a reduction of primary graphite altogether. As has been discussed earlier, this rapid decrease of the primary graphite is probably a result of dissolution of suitable substrates for graphite to nucleate on with increasing holding time.

Fig. 16

The total volume fraction of the approximated subpopulations $v_{1}^{\ast}$ through $v_{5}^{\ast}$ as a function of holding time. The numbers correspond to the A_i factor found in Table III

Eutectic Graphite Nodules

The smaller mean value of $v_{3}^{\ast}$ implies that these nodules formed at a later stage than $v_{4}^{\ast}$ and $v_{5}^{\ast}$. It has been proposed that nucleation of eutectic nodules occurs in the field of rejected carbon ahead of growing austenite dendrites.[11] Dendritic structure was confirmed by selective tinting of cross sections, as was shown in Figure 9. If $v_{3}^{\ast}$ nucleated ahead of the dendritic front, this would mean that dendrites grew into a melt populated by both primary and eutectic nodules. Assuming both nodules interact with the growing austenite similarly, the spatial distribution is therefore on the microscale expected to be similar for primary and eutectic nodules. It is difficult to convincingly verify that our experiments are in agreement with this expectation since cross sections of the specimens do not reveal the true volumetric diameter of the particles. However, Figure 15 provides at least an indication by showing no striking difference in distribution among spheroids with diameters larger than 70 µm (on the cross section). Spheroids larger than 90 µm are often found near smaller spheroids.

Moreover, Figure 17 shows that nodules of diameters in the size range of primary and eutectic nodules (>70 µm) were often found aligned with primary dendrite arms. Graphite nodules have been observed in contact with austenite in quenched SGI without being enveloped.[34,35] This indicates that austenite does not necessarily envelop the nodules immediately on contact. One explanation which has been proposed is that the barrier to nucleation of the secondary phase causes the melt composition to drift past the eutectic composition due to precipitation of the primary phase.[32] Once the barrier is surpassed, the liquid is more undercooled with respect to the secondary phase which may grow independent for a period until eutectic composition is restored and the eutectic growth can proceed in a more typical fashion. It has also been pointed out that a given undercooling with respect to austenite translates to a larger supersaturation than does the same undercooling with respect to graphite due to the larger slope of the graphite liquidus line.[27]

Fig. 17

Cross section of H10 tinted with Motz[21] picric solution. The diameter of an arbitrary nodule is given to emphasize scale (Color figure online)

The alignment of primary and eutectic nodules along primary arms does however suggest that they are enveloped or trapped by the growing austenite dendrites. Entrapment of free graphite in the dendritic austenite could be encouraged by liquid flow against the growth direction of the dendritic austenite due to shrinkage. The similar tint of the dendrites and the matrix surrounding the nodules suggests that they were enveloped, if not immediately on contact, not long after the dendrites had formed. Using centrifugal experiments, it has been shown that buoyancy causes nodules to float against the pressure gradient and accumulate on the side of the dendrites which is first encountered.[32] This may explain why in this work the aligned nodules are often found dominant on one side of the primary arm such as in Figure 17.

The roughly constant mode and width of $v_{3}^{\ast}$ indicates that apart from reducing the total number and volume of eutectic nodules, the parallel development of the vermicular eutectic does not interfere considerably with the development of the nodular eutectic. In agreement with this interpretation, nodular and vermicular graphite is found mostly segregated in the microstructure as can be seen in Figures 15 and 18. Nodules are most of the time found in areas between vermicular eutectic cells, and are rarely found inside them. This could be explained either by most spheroidal graphite having nucleated after considerable growth of vermicular graphite, or by spheroidal graphite floating or being pushed away from the growing vermicular eutectic into the remaining liquid. However, both explanations appear contradictory to the observation that the bright blue tinting around most spheroidal graphite indicates that they were surrounded by austenite, and thereby locked in place, at an early stage of solidification.

Fig. 18

Cross section of H60 tinted with Motz[21] picric solution (Color figure online)

Late Graphite Nodules

A third small subpopulation $v_{2}^{\ast}$, is most pronounced in H50 and H60 in Figure 13. The small size indicates that these nucleated at a late stage of solidification. This may relate to signs of a late reaction denoted for H40, H50, and H60 around 1406 K (1133 °C) in Figure 7. A third, late subpopulation of spheroidal graphite has been recognized in SGI by others.[7,10,11,12] A plausible explanation for this population appearing in the low nodularity specimens is that the relatively rapid growth of the vermicular eutectic interferes with the continuous nucleation of graphite nodules. Continuous nucleation of new nodules through most of solidification has been reported for SGI[5,36] and cast irons with 40 to 50 pct nodularity.[37] It appears reasonable that, for a given moderate cooling rate and nucleation potential, there will exist a nodularity where the vermicular eutectic, with its higher growth velocity, generates more heat than dissipating from the casting. This would then lead to a reduced undercooling and a discontinuation of nucleation. The undercooling may at a later stage exceed the prior maximum due to factors like grain impingement, which triggers a new nucleation event.

However, if $v_{2}^{\ast}$ nucleated at T3, nodules of this size are expected to be concentrated to the last areas to freeze. Such areas are identified by their pale yellow tint between vermicular cells and dendrite arms in Figures 18 and 19. Contrary to expectation, graphite nodules appear to be rare in these areas. Evidence for a late stage nucleation of graphite nodules is for this reason regarded inconclusive in this study.

Fig. 19

A closer look at H60 shown in Fig. 9. (a) The peripheral layer and (b) closer to the center (Color figure online)

Spatial Distribution on the Macro Scale

In this work, the spatial distribution of graphite over the cross section was not studied closely, however it is relevant to address the possibility that the nodule subpopulations do not populate the castings uniformly. Other authors have noted a considerable difference in morphology and graphite size distribution between the central region and closer to the surface of the casting.[9,37] A peripheral layer can be distinguished in Figure 9, especially for H60, extending about 6 mm into the specimen. The layer features larger vermicular eutectic cells than closer to the center of the specimen. A closer view of the two regions is available in Figures 19(a) and (b). However, the layer becomes increasingly difficult to distinguish as nodularity increases. It appears unwise to mix data from the peripheral layer with data from the central region as was done in this study. Future work should avoid this, either by focusing on one or the other or by analyzing them separately.

Conclusions

A hypereutectic SGI has been remelted using varying holding time at 1723 K (1450 °C) protected by Ar, and then solidified inside the furnace. The nodularity of the solidified specimens decreased from above 80 pct at 10 minutes holding time to below 20 pct at 60 minutes holding time. Sectional size distributions of graphite nodules were measured on cross sections of the specimens and translated to volumetric size distribution by volume fraction. These were then approximated as a sum of subpopulations of Gaussian distributions to investigate the subpopulations which constitute the graphite nodule populations. Below are the main conclusions from the results.

• 1. For a holding time of 10 minutes corresponding to an average nodularity of 86.2 pct, it was possible to distinguish two subpopulations of approximately equal volume fraction which together accounted for most of the graphite by volume fraction. Cooling curves based on the hypereutectic composition and an early reaction prior to the eutectic arrest, the larger of the two subpopulations is likely primary graphite. The subpopulation of smaller nodules was consequently judged to have formed during the eutectic stage of solidification.

• 2. As the holding time was increased the volume fraction of both subpopulations decreased due to the increasing portion of vermicular graphite. By a holding time of 40 minutes, corresponding to an average nodularity of 46.7 pct, the subpopulation of primary nodules has shrunk to a size comparable to noise, making eutectic nodules the dominant population by volume and number. The volume of eutectic nodules continued to shrink until the longest tested holding time of 60 minutes, corresponding to an average nodularity of 14.5 pct.

• 3. The mode and standard deviation of the primary and eutectic nodules were approximately constant, independent of nodularity. Nodules were also rarely found incorporated in cells of vermicular graphite, but were typically found in the space around them. This suggests that the influence of the growth of the vermicular eutectic on the development of the nodular eutectic was small.

• 4. A small third subpopulation of graphite nodules was recognized in specimens with low nodularity. Similarly, a late stage reaction was indicated by features on the cooling curves for the same specimens. However, small nodules were scarce in the last regions to freeze, making it difficult to associate the two.

• 5. Two maxima appeared on the cooling curve during the eutectic arrest for specimens with the shortest holding time and the lowest nodularity. While others have attributed this to the early stage of the eutectic reaction featuring dendritic growth of austenite, dendritic structure was distinguished in all specimens, regardless of the shape of the cooling curves during eutectic arrest.