Study on the Equilibrium Between Liquid Iron and Calcium Vapor

Abstract

The solubility of calcium in liquid iron at 1823 K and 1873 K (1550 °C and 1600 °C) as a function of calcium potential was studied experimentally. The measurements were performed using a closed molybdenum holder in which liquid calcium and liquid iron were held at different temperatures. The results indicate a linear relationship between the activity of calcium, relative to pure liquid calcium, and the mole fraction of dissolved calcium in liquid iron, with a negligible temperature dependency in the ranges studied. The activity coefficient of calcium in liquid iron at infinite dilution, $\gamma_{{{\text{Ca}}({\text{l}})}}^{ \circ } ,$ was calculated as 1551.

Introduction

An important focus for the steel industry in order to improve material properties and decrease problems during processing is control of the population of non-metallic inclusions. Calcium addition in the ladle, referred to as calcium treatment, is a common method for modification of alumina-containing inclusions into liquid calcium aluminate inclusions. The possibility of modification of inclusions via the top slag has also been discussed. Due to the high vapor pressure of liquid calcium at steelmaking temperatures as well as the very low solubility of calcium in liquid steel, it is challenging to perform calcium treatment in an efficient and, with respect to different heats, consistent manner. In order to achieve this, knowledge of the thermodynamic properties of calcium dissolved in steel at steelmaking temperatures is essential to appropriately describe the reactions involving calcium taking place between steel and slag and steel and non-metallic inclusions. Several researchers have studied the iron-rich side of the iron-calcium system at temperatures in the range of 1823 K to 1880 K (1550 °C to 1607 °C) using different experimental techniques.[1,2,3,4] Due to the high vapor pressure of calcium in the temperature range of interest and the stability of calcium oxide, the studies have been performed in closed or pressurized systems. In order to determine the activity coefficient of calcium in liquid iron, Song and Han[1] studied the solubility of calcium in liquid iron in equilibrium with varying calcium vapor pressures at 1873 K (1600 °C), while Fujiwara et al.[2] studied the partitioning of calcium between liquid iron and liquid silver at 1823 K (1550 °C). Köhler et al.[3] and Sponseller and Flinn[4] studied the solubility of calcium in liquid iron in contact with liquid calcium at 1873 K and 1880 K (1600 °C and 1607 °C) in pressurized systems. While the previous studies cover a relatively wide composition range, viz. 0.3 to 320 ppm by weight, there are some disagreements and scatter in the data, especially at lower calcium contents. The aim of the present study is to provide additional data on the solubility of calcium in liquid iron under varying calcium potentials at steelmaking temperatures.

Experimental

Experimental measurements were made in order to study the dissolved calcium content in iron after equilibration with calcium vapor. The principle of the experiments was to equilibrate iron and calcium held at different temperatures in a closed container. By varying the temperature of the calcium, and thus the vapor pressure of calcium in the container, the iron was subjected to different calcium potentials.

A schematic overview of the experimental setup is shown in Figure 1. A vertical resistance furnace with super Kanthal heating elements and an alumina reaction tube was used. To ensure efficient cooling of the samples without withdrawing them from the furnace, the top of the reaction tube was internally connected to a water-cooled aluminum chamber. By suspending the samples from a steel rod connected to a computer-controlled lifting system, the samples could be raised quickly into the cooling chamber after equilibration. The lower end of the reaction tube was connected to a smaller aluminum chamber. O-rings and radial seals were used to seal the reaction chamber. Gas was introduced in the lower aluminum chamber and led out through an outlet situated in the cooling chamber. An extra gas inlet in the cooling chamber allowed for introduction of gas at a high flow rate directly to the samples during cooling. The gas flow rates were controlled using Bronkhorst flow meters. The furnace temperature was controlled by a Eurotherm controller using a type B thermocouple (70 pct Pt/30 pct Rh-94 pct Pt/6 pct Rh). The temperatures of the iron and the calcium, respectively, were measured using two individual type B thermocouples.

Fig. 1

Experimental setup

A molybdenum container with a conical closing at the lower end was used to hold the calcium and the iron (see inset in Figure 1). The upper end of the molybdenum chamber was closed, while the lower part of the cylinder was threaded externally. In order to seal the container, a conical molybdenum plug was pushed into the open end of the cylinder and secured by an internally threaded molybdenum cup. The conical plug was also used as a holder for the calcium. The iron was kept in the upper part of the container supported by a molybdenum rod. By varying the length of the support rod, the distance between the iron and the calcium, and thus the temperature of the calcium, could be varied. In each individual run, the temperatures of both the calcium and the iron were kept constant. It was previously shown that the use of a molybdenum container with conical closing allowed for the release of overpressure during heating while being able to maintain a constant moderate vapor pressure in the container thereafter.[5]

To accurately measure the temperature of the calcium, the holder was designed with a central channel allowing for insertion of a thermocouple with its tip level with the calcium. The temperature of the iron was measured using a second thermocouple placed just outside the container, level with the iron.

For each run, 10 g of iron powder (99.9 pct, supplied by Alfa Aesar) was held in H₂ gas (99.995 pct, supplied by AGA) for 60 minutes at 773 K (500 °C) to reduce surface oxides. The iron powder was placed in a CaO crucible (99.9 pct, supplied by TEP Ceramics) and inserted in the molybdenum container. The container was sealed with the conical plug, holding 4 g of calcium granules (99.5 pct, supplied by Alfa Aesar), and the internally threaded cup. The container was connected to the lifting system with a molybdenum extension rod and inserted into the hot zone of the furnace. Before sealing the furnace, the positions of the measurement thermocouples were adjusted. The furnace was evacuated for 3 hours using a vacuum pump and refilled with argon gas (99.999 pct, supplied by AGA). An argon flow of 0.1 L/min was employed throughout the experiments. The furnace was heated at a rate of 1.6 K/min to the target temperature and held for 48 hours. After equilibration, the molybdenum container was quickly raised into the cooling chamber. To enhance the cooling, a high flow of argon gas (1 L/min) was injected directly into the cooling chamber.

After each experiment, the iron was removed from the crucible and ground and polished thoroughly to obtain clean pieces without any surface oxides for analysis. Approximately 2 g of iron from each experiment was dissolved and analyzed using ICP-SFMS (Thermo Fischer Element XR). The relative error in the chemical analysis is given as less than 20 pct. To ensure that no significant amount of inclusions was present to affect the chemical analyses, iron samples were carefully examined manually in scanning electron microscope (Hitachi S-3700N with a Bruker EDS analyzer). Samples were also examined in scanning electron microscope with automated inclusion microanalysis using INCA Feature.

Results

Two different temperatures at which the iron was held were used in the experiments, viz. 1823 K and 1873 K (1550 °C and 1600 °C). A number of temperatures at which the calcium was held were employed. Table I lists the experimental conditions for each experiment along with the analyzed calcium contents. The vapor pressure of calcium in the container for each experiment was calculated based on the measured temperature of the liquid calcium. The saturated vapor pressure of pure liquid calcium as a function of temperature is given by Knacke et al.[6] as

$$ \log \;p_{\text{Ca(l)}}^{ \circ } = \frac{ {-} 9103}{T} - 1.71 \times \log (T) + 10.688, $$

(1)

where $p_{{{\text{Ca}}({\text{l}})}}^{ \circ }$ is given in bar and T is given in K. Under the present experimental conditions, the calculated vapor pressures of calcium in the container varied between 0.00328 and 0.0139 MPa resulting in calcium contents between 8.3 and 37.6 ppm by weight in iron. It should be noted that the calculated calcium vapor pressures, and thus any derived value, depend on the reference data used. The iron samples were carefully examined in a scanning electron microscope to ascertain that the results of the chemical analyses were not affected by the existence of calcium-containing inclusions. Apart from using automated inclusion microanalysis, a number of randomly chosen positions in the bulk of the iron samples were examined. As an example, Figure 2 shows SEM micrographs from the bulk of Sample 6 including calcium and oxygen mappings. Some small pores and carbon-containing particles, most likely originating from sample preparation, could be seen in the samples. No calcium-containing inclusions were found, indicating that the holding time was sufficient with respect to floatation of inclusions and that the analyzed calcium contents of the samples mainly represent dissolved calcium.

Table I Experimental Conditions and Analysis Results

Fig. 2

SEM micrographs of Sample 6 including elemental mapping

Discussion

The results from the chemical analyses show a clear increase of the calcium content in iron with increasing temperature of the calcium. The increase of dissolved calcium in the iron phase evidently indicates an increasing vapor pressure of calcium in the container, suggesting therefore that the calcium potential during the experiments was controlled by the vapor pressure from the liquid calcium, as intended.

The reproducibility of the experiments is exemplified by the analyzed calcium contents of Samples 3 and 4 shown in Table I, as these two experiments were conducted under similar experimental conditions. The results are in good accordance. In general, the scatter in the results from the chemical analyses is low. However, the main source for experimental uncertainties is expected to be the chemical analysis, considering the given relative error.

Assuming that the calcium vapor behaves as an ideal gas, the activity of calcium, relative to pure liquid calcium, can be expressed as

$$ a_{\text{Ca(l)}} = \frac{{p_{\text{Ca(l)}} }}{{p_{\text{Ca(l)}}^{ \circ } }} = X_{\text{Ca}} \times \gamma_{\text{Ca(l)}} , $$

(2)

where p _Ca(l) is the vapor pressure of calcium at a given temperature, $p_{{{\text{Ca}}({\text{l}})}}^{ \circ }$ is the saturated vapor pressure of pure liquid calcium at the same temperature, X _Ca is the mole fraction of calcium in solution, and γ _Ca(l) is the activity coefficient of calcium relative to pure liquid calcium. Data on the saturated vapor pressure of calcium at temperatures above the boiling point of calcium are scarce. The values of $p_{{{\text{Ca}}({\text{l}})}}^{ \circ }$ at 1823 K and 1873 K (1550 °C and 1600 °C) used for the present discussion are extrapolated based on Eq. [1].

The calculated values of X _Ca and a _Ca(l) based on the experimental results and the assumption that the activity of the liquid calcium held in the lower part of the molybdenum container is equal to unity are shown in Table II.

Table II Calculated Values of X _Ca and a _Ca(l)

The activity of calcium relative to pure liquid calcium is plotted against the mole fraction of calcium in liquid iron in Figure 3(a). It is seen that the dependence of the activity coefficient on temperature is negligible in the temperature range studied.

Fig. 3

Activity of calcium relative to liquid calcium plotted against mole fraction of calcium in iron, (a) present data and (b) comparison with data from Song and Han[1] and Fujiwara et al.[2] The dashed line represents the linear least square regression of the present data and data from Song and Han

A comparison of the present results with values based on the data from Song and Han[1] as well as Fujiwara et al.[2] is presented in Figure 3(b). The activity coefficient of calcium in silver was calculated based on the data by Fischbach,[7] as suggested by Fujiwara et al.[2] It should be mentioned that only data below 110 ppm calcium in iron are included in the plot as the focus of the present study is on lower calcium contents. As shown in Figure 3(b), the presented data show a similar trend where the effect of temperature on the activity coefficient is small and the dependency of the activity of calcium on the mole fraction of calcium in iron can be approximated by a linear relationship reasonably well in the composition range studied. It can, however, be noted that the activities evaluated based on iron-silver equilibration are somewhat higher compared to the studies based on iron-calcium vapor equilibration. Assuming that the observed linear relationship between the activity of calcium and the mole fraction of calcium is valid as the mole fraction of calcium approaches zero, a linear least square regression based on data obtained using iron-calcium vapor equilibration was made. The slope of the resulting regression line, shown in Figure 3(b), gives the activity coefficient of calcium in liquid iron at infinite dilution, $\gamma_{{{\text{Ca}}({\text{l}})}}^{ \circ } ,$ as 1551. Considering the large positive deviation from ideality exhibited by calcium in iron, it is reasonable to expect a higher activity coefficient at lower temperature. However, as mentioned above, no such effect can be seen between 1823 K and 1873 K (1550 °C and 1600 °C) from the present data. Corresponding linear least square regression based on data from iron-silver equilibration[2] gives a value of 2162 for the activity coefficient of calcium in liquid iron at infinite dilution. A possible explanation for the observed difference between the data based on different experimental techniques could be the uncertainties related to the data for the activity coefficient of calcium in liquid silver. The equation suggested by Fujiwara et al.[2] is based on extrapolation from data by Fischbach[7] obtained at 1123 K to 1273 K (850 °C to 1000 °C). Measurements in the temperature range of 1570 K to 1831 K (1297 °C to 1558 °C) by Wakasugi and Sano[8] and Tago et al.,[9] using equilibration of silver with CaC₂- and CaO-saturated slags, respectively, indicate a lower activity coefficient of calcium in silver compared to the extrapolated values based on Fischbach[7] data. At 1823 K and a mole fraction of calcium in liquid silver of 0.01, the extrapolated value is approximately 20 times higher than the experimental values. While the data by Wakasugi and Sano[8] and Tago et al.[9] cannot explain the difference between the values based on iron-calcium vapor equilibration and the values based on iron-silver equilibration, it indicates the possible uncertainties associated with the available data concerning the activity coefficient of calcium in liquid silver at higher temperatures.

Using the activity coefficient of calcium calculated based on iron-calcium vapor equilibration, it is possible to estimate the level of dissolved calcium in liquid iron during steelmaking on the basis of the following reaction,

$$ {\text{Ca}}({\text{l}}) + {\text{O}}_{{(1\;{\text{wt}}\;{\text{pct}}\;{\text{in}}\;{\text{Fe}})}} = {\text{CaO}}({\text{s}}). $$

(3)

The standard Gibbs free energy of the reaction can be calculated based on the following reactions:[10]

$$ {\text{Ca}}({\text{l}}) + \frac{1}{2}{\text{O}}_{2} ({\text{g}}) = {\text{CaO}}({\text{s}}), $$

(4)

$$ \Updelta G_{4}^{ \circ } = {-} 640,152 + 108.6 \times T\;{\text{J}}/{\text{mol}} , $$

(5)

$$ \frac{1}{2}{\text{O}}_{2} ({\text{g}}) = {\text{O}}_{{(1\;{\text{wt}}\;{\text{pct}}\;{\text{in}}\;{\text{Fe}})}} , $$

(6)

$$ \Updelta G_{6}^{ \circ } = {-} 117,152 - 2.887 \times T\;{\text{J}}/{\text{mol}}. $$

(7)

The resulting standard Gibbs free energy for Reaction [3] is

$$ \Updelta G_{3}^{ \circ } = {-} 523,000 + 111.5 \times T\;{\text{J}}/{\text{mol}} . $$

(8)

The equilibrium constant for Reaction [3] can be written as

$$ K_{3} = \frac{{a_{\text{CaO(s)}} }}{{a_{{{\text{Ca}}({\text{l}})}} \times a_{{{\text{O(}}1\;{\text{wt}}\;{\text{pct}}\;{\text{in}}\;{\text{Fe}})}} }}. $$

(9)

Based on Eq. [9], the maximum content of dissolved calcium can be calculated assuming that the steel is in equilibrium with a calcium oxide-saturated slag (a _CaO(s) = 1). It is well known that the oxygen activity, relative to the 1 wt pct in iron standard state, in an aluminum-killed steel is in the range of 1 to 3 × 10⁻⁴. Assuming a _{O(1 wt pct in Fe)} = 1 × 10⁻⁴, the calcium activity relative to pure liquid calcium is calculated as 1.7 × 10⁻⁵, corresponding to a mole fraction of calcium of 1.1 × 10⁻⁸ or 0.008 ppm (by weight). The extremely low calcium content in the steel would rule out the possibility of using slag to modify inclusions with respect to calcium oxide, since the mass transfer of calcium in the steel would be very slow.

It is worthwhile to mention that the estimated maximum content of dissolved calcium (0.008 ppm) is approximately 1000 times lower than the lowest calcium contents obtained in the present study. This estimation indicates a strong need for more experimental data at even lower calcium contents in order to correctly describe reactions involving calcium in ironmaking and steelmaking. A good chemical analysis technique is essential to make this investigation.

Although the content of dissolved calcium during iron and steelmaking is extremely low, as seen above, it is still of great interest to consider the solubility of calcium in liquid iron in contact with pure liquid calcium. As discussed in the introduction, calcium treatment is commonly used by many steel producers. It is expected that the calcium activity would vary with the position in the steel bath with respect to the calcium addition. Nevertheless, knowledge of the maximum theoretical calcium content which can be achieved locally during calcium treatment of steel is essential. Neglecting the effects of the other dissolved elements, a rough estimation of the dissolved calcium content of liquid iron in contact with pure liquid calcium in the temperature range of 1823 K to 1873 K (1550 °C to 1600 °C) can be made. Assuming an activity of calcium relative to pure liquid calcium of one and an activity coefficient of calcium of 1551, the solubility of calcium in iron is calculated to be (in mole fraction of calcium) 6.45 × 10⁻⁴ or 463 ppm (by weight). A comparison of the estimated value with earlier experimental results and estimated values is presented in Table III. It can be seen that the values are in the same order of magnitude with a variation between 320 and 463 ppm by weight. It should, however, be noted that for calcium treatment these estimated values only apply to situations where the total pressure exceeds the saturated vapor pressure of liquid calcium. At pressures close to atmospheric pressure, the solubility of calcium would be considerably lower.

Table III Solubility of Calcium in Liquid Iron in Equilibrium with Pure Liquid Calcium

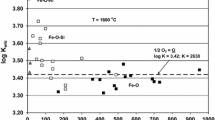
Assuming local equilibrium, the steel at the calcium addition would be saturated with calcium (300 to 500 ppm by weight). A short distance from the calcium addition, the calcium activity would be very low, resulting in a very low dissolved calcium content in the steel (in the order of 0.01 ppm by weight). To illustrate this aspect, Figure 4 presents the mole fraction of calcium as a function of log a _Ca(l) at 1873 K (1600 °C) based on the experimental results from iron-calcium equilibration. As the added calcium is being vaporized and the calcium vapor escapes, the condition of the steel being in equilibrium with pure liquid calcium vanishes. As Figure 4 evidently shows, the steel is supersaturated with respect to calcium just after the calcium addition.

Fig. 4

Mole fraction of calcium plotted as a function of the logarithm of the activity of calcium relative to pure liquid calcium (dashed line) at 1873 K (1600 °C) including data from the present study and data from Song and Han[1]

Summary

Experimental measurements were made in order to study the solubility of calcium in liquid iron at different calcium potentials at 1823 K and 1873 K (1550 °C and 1600 °C). A linear relationship between the activity of calcium, relative to pure liquid calcium, and the mole fraction of dissolved calcium in liquid iron was obtained in the composition range studied (8.3 to 37.6 ppm by weight). No clear temperature dependency was observed. Assuming that the linear relationship was valid as the mole fraction of calcium approaches zero, the activity coefficient of calcium in liquid iron at infinite dilution, $\gamma_{{{\text{Ca}}({\text{l}})}}^{ \circ } ,$ was calculated as 1551. Based on the present results, the expected dissolved calcium content in steel is in the order of 0.01 ppm by weight. This indicates that there is a strong need for more experimental data at lower calcium contents in order to make the measurements truly useful in the steelmaking process. The present results also indicate that an optimization of the secondary steelmaking process regarding calcium treatment needs to consider the calcium loss and rate of mass transfer.