Introduction

Ceramic foam filters (CFFs) are commonly used in various industries, including chemical, automotive, and metallurgy, for catalyst support, to control exhaust emissions, and for liquid metal filtration.[1–4] In general, solid foams can be divided into open and closed cell materials, where each material has a different structure, property, and application.[2,5,6] Depending on the type and production method, ceramic foams may possess adequately high mechanical properties such as high thermal and chemical resistance, high structural uniformity, and strength.[6]

The open cell ceramic foams represent a net of voids where each and all voids are surrounded by and connected via a ceramic material,[2,7] as shown in Figure 1(a). Due to open pores, the foams have high permeability and, therefore, are able to capture solid particles. This makes CFFs suitable for filtration in metal production.[5,6] On the other hand, closed cell foams are polyhedron-like cells connected via a solid interface while each cell is isolated from the others,[2,7] as illustrated in Figure 1(b). Such structure creates a suitable material for thermal insulation, fire protection, gas combustion burners, etc.[5,6] In this research, the focus was on the open cell 30, 50, and 80 pores per inch (PPI) commercial alumina CFFs.

Fig. 1
figure 1

Schematic view of cellular materials: (a) open cell and (b) closed cell

Full size image

In metallurgy, CFFs are used to remove undesired nonmetallic particles from molten metal before casting,[1,4,7–13] i.e., filtration. In order to prime the filters, the melt has to reach a certain pressure on the top of the filter to initiate passage through the filter.[9–12,14] To estimate, adjust, and maintain the required pressure and to regulate the melt velocity, it is essential to determine the Darcy and non-Darcy permeability coefficients of the filter.[8,9,15] The permeability coefficients can be obtained using permeametry experiments.[16–18] In general, permeametry is based on a gas or liquid flow through a porous media. Thus, the pressure drop ∆P (Pa) along the height of the porous media L (m) as a function of the superficial velocity V s (m/s) needs to be measured. Thereafter, the Darcy and non-Darcy permeability coefficients k 1 (m2) and k 2 (m) can be estimated using the Forchheimer equation for incompressible fluids (Eq. [1]),[2,8,9,15,17,19–21] if the fluid dynamic viscosity µ (Pa s) and fluid density ρ (kg/m3) values are known:

$$ \frac{\Delta P}{L} = \frac{{\mu V_{\text{s}} }}{{k_{1} }} + \frac{{\rho V_{\text{s}}^{2} }}{{k_{2} }} $$
(1)

In the literature,[8,9,17,18,22–32] it has been stated that accurate pressure drop estimates only can be achieved when fluid bypassing is avoided. If the CFF samples are not fully sealed, fluid will flow through the filter as well as the gap between the filter and filter holder. This results in an underestimation of the pressure gradient and the Darcy and non-Darcy permeability coefficients. Therefore, it is necessary to adequately seal the filters prior to the permeametry experiments. Table I summarizes the different methods that researchers used to prevent bypassing. However, it should be noted that the effect of fluid bypassing may not yet be expressed in numbers. In recent work, it is aimed at studying the effect of fluid bypassing on the pressure gradient as well as the empirically obtained Darcy and non-Darcy permeability coefficients. In addition, the well-sealed and unsealed permeametry experiments were mathematically modeled to explain the results.

Table I Different Methods That Have Been Used to Avoid Fluid Bypassing
Full size table

Method

Experimental Procedure

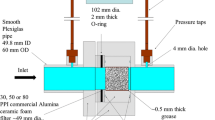
Permeametry characteristics of commercial alumina CFFs of 30, 50, and 80 PPI were examined using water in the temperature range of 282 K to 284 K (9 °C to 11 °C). The experimental setup includes a submersible pump, a pressure transducer, a Plexiglas filter holder, 49.8-mm-diameter smooth pipes (outer diameter), a pressure transducer, a digital multimeter, a T-type thermometer, a National Instruments NI USB-TC01 data logger, an OHUAS T31P scale, a container, and CFFs of different PPI. Nine filter samples, three ~51-mm-diameter samples from 9-in. ~50-mm-thick filters for each PPI, were cut by using a computer numerical control water jet machine. Samples were divided in three groups. Thereafter, the samples were manually resized to about 49.5-mm diameter to fit into the filter holder, as explained elsewhere.[9] Group 3 of the samples was used to study the effect of fluid bypassing on permeametry parameters of the 30, 50, and 80 PPI CFFs. Therefore, the liquid permeametry experiments were performed first on the unsealed samples. Then the samples were dried at room temperature for 2 days before being sealed. The sealing procedure was done in three steps: (1) blocking of the side walls of the samples, (2) resizing, and (3) wrapping in grease-impregnated cellulose fibers.[9,15]

A Plexiglas filter holder was used to hold the filters, and pressure drop measurements were done using a DF-2 (AEP, Transducer, Italy) pressure transducer as the water circulated through the apparatus and the filters (Figure 2). The fluid velocity was calculated based on the mass flow measured during the experiment using the weight gain in a container, with a maximum capacity of 53 kg of water. In addition, the temperature was measured using a FLUKE 80PT-25 T-Type probe. The details of the experimental procedure can be found elsewhere.[9,15]

Fig. 2
figure 2

Experimental apparatus.[8,9,15]

Full size image

In total, two sets of permeametry experiments were performed using both the unsealed and well-sealed 30, 50, and 80 PPI samples. The pressure gradient profiles as a function of the mean fluid superficial velocity for both the well-sealed and unsealed samples were obtained, and the Darcy (k 1) and non-Darcy (k 2) permeability coefficients were empirically calculated, based on the Forchheimer’s equation (Eq. [1]). The Ergun’s approach, i.e., dividing the Forchheimer equation (Eq. [1]) by superficial velocity and applying a linear regression, was used to estimate the permeability coefficients. The approach was found to be the appropriate method for obtaining the coefficients.[8,15,33]

Mathematical Modeling

To mathematically model the permeametry experiments of the 30, 50, and 80 PPI CFF samples, two-dimensional (2D) axisymmetric simulations were conducted using COMSOL Multiphysics 5.1 software. Two models were created to simulate the well-sealed and unsealed 30, 50, and 80 PPI samples, as presented in Figures 3(a) and (b). In both models, an inlet pipe is connected to the top of the filter and an outlet pipe to the lower part of the filter. In the well-sealed model, there is no gap between the filter and filter holder (Figure 3(a)). As a result, fluid only enters the model from the top, flows through the filter, and leaves the filter and model from the opposite side. In the unsealed model, a gap between the filter and filter holder was introduced (Figure 3(b)). To be specific, the introduced gap is equal to the difference between the measured inner diameter of the filter holder, 50 mm, and the average measured diameter of the filters used in the experiments. In the unsealed model, fluid also enters the model from the top, flows through the filter and gap, and leaves the filter and gap and the model from the opposite side. In addition, free flow between the filter and gap is also allowed.

Fig. 3
figure 3

Schematic view of the 2D axisymmetric CFD models: (a) well-sealed condition and (b) unsealed condition

Full size image

The model dimensions were set to the mean values of the actual filter dimensions (Table II) and the experimental apparatus dimensions. The dimensions were measured using a caliper with a resolution of 0.01 mm, and the mean values represent an average of 10 readings with a confidence interval of 95 pct. Fluid and porous media properties, for both the well-sealed and unsealed models, including fluid temperature, fluid density and dynamic viscosity, filter open pore porosity, and the Darcy and non-Darcy coefficients, were set consistent with the experimental data explained elsewhere.[9,15]

Table II Filter Dimensions[9,15]
Full size table

Solution Technique, Transport Equations, and Assumptions

The Reynolds numbers for both the well-sealed and unsealed permeametry experiments were calculated to be in the range of 2500 to 26,000 and 5750 to 32,400, respectively.[15] Therefore, the turbulent flow computational fluid dynamics (CFD) simulations were performed.

To simulate the turbulent flow for incompressible fluids with an added porous media domain in COMSOL Multiphysics 5.1, “The Turbulent flow, Algebraic yPlus Interface” module was used. It should be noted that the commonly used turbulent modules, k–ɛ, k–ω, etc., were not yet available in the porous media domain, as elucidated in COMSOL Multiphysics 5.1. Therefore, the following governing transport equations in the free flow and porous region for an incompressible fluid in a steady-state condition need to be solved.

  1. (1)

    Free flow region—Reynolds-Averaged Navier–Stokes (RANS) equations for incompressible fluids, containing continuity (Eq. [2]) and conservation of momentum (Eq. [3]).[34–38]

  2. (2)

    Porous region—continuity equation (Eq. [2]) together with the Reynolds-Averaged Brinkman–Forchheimer equation (Eq. [4]):[34,35,38–42]

$$ \frac{\partial }{{\partial x_{i} }}\left( {\rho U_{i} } \right) = 0 $$
(2)
$$ \rho U_{j} \frac{{\partial U_{i} }}{{\partial x_{j} }} = - \frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial U_{i} }}{{\partial x_{j} }} + \frac{{\partial U_{j} }}{{\partial x_{i} }}} \right) - \rho \overline{{u^{\prime}_{i} u^{\prime}_{j} }} } \right] $$
(3)
$$ \rho U_{j} \frac{{\partial U_{i} }}{{\partial x_{j} }} = - \frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial U_{i} }}{{\partial x_{j} }} + \frac{{\partial U_{j} }}{{\partial x_{i} }}} \right) - \rho \overline{{u^{\prime}_{j} u^{\prime}_{i} }} } \right] - \varepsilon \frac{\mu }{k}U_{i} - \varepsilon \beta \left[ {\sqrt {U_{j} U_{j} } U_{i} + \frac{{U_{j} }}{{\sqrt {U_{j} U_{j} } }}\overline{{u^{\prime}_{j} u^{\prime}_{i} }} } \right] $$
(4)

where ρ is density, U i is the time-averaged mean velocity in the x i direction, U j is the time-averaged mean velocity in the x j direction, P is pressure, µ is the dynamic viscosity, ɛ is the filter porosity (here, open pore porosity was used), \( \left( { - \rho \overline{{u^{\prime}_{j} u^{\prime}}}_{i} } \right) \) is the Reynolds stress tensor τ xy , k is the Darcy drag term, and β is the Brinkman–Forchheimer drag coefficient. Equation [3] consists of convection in the left-hand side and the following terms in the right-hand side: pressure gradient, viscous diffusion, and turbulent diffusion. In addition to the terms explained for Eq. [3], the two additional terms in the right-hand side of Eq. [4] are the Darcy and Forchheimer terms. The terms represent resistance to fluid flow in the porous media.

In order to close Eqs. [2] through [4], the Reynolds stress tensor has to be estimated with the aid of a turbulence model.[38] The Reynolds stress tensor (τ xy ) can be expressed as a function of eddy or turbulent viscosity,[36–38] as presented in Eq. [5]. According to the Prandtl’s mixing length hypothesis, the eddy viscosity is also expressed as a function of mixing length, as in Eq. [6]. In this hypothesis, it is assumed that a lump of fluid repositioning in the transverse direction retains its mean properties for the characteristic length of l mix until it mixes with its surroundings.[15,36,37,43] In this theory, the mixing length (l mix) is also correlated to the distance y from the wall (Eq. [7]) with the proportionality constant κ, i.e., Kármán constant, to be ≈0.41.[15,36,37,43]

$$ \tau_{ij = } - \rho \overline{{u^{\prime}_{i} u^{\prime}_{j} }} \approx \mu_{\text{T}} \frac{{{\text{d}}U}}{{{\text{d}}y}} $$
(5)
$$ \mu_{\text{T}} \approx \rho l_{\text{mix}}^{2} \left| {\frac{{{\text{d}}U}}{{{\text{d}}y}}} \right| $$
(6)
$$ l_{\text{mix}} \approx \kappa y $$
(7)

In the literature,[44–47] the Brinkman–Forchheimer drag term (β) in the Brinkman–Forchheimer equation (Eq. [4]) is defined by fluid density ρ (kg/m3), geometric function F (dimensionless), porosity ɛ (dimensionless), and Darcy permeability coefficient k (m2), as shown in Eq. [8]. Based on Ergun’s experimental findings on packed beds, the geometric function F and Darcy permeability coefficient k can be related to the porosity and particle diameter (Eqs. [9] and [10]).[44–47] Here, the Darcy permeability coefficient (k) is the same Darcy permeability coefficient (k 1) in Eq. [1].

$$ \beta = \frac{\rho F\varepsilon }{\sqrt k } $$
(8)
$$ F = \frac{1.75}{{\sqrt {150\varepsilon^{3} } }} $$
(9)
$$ k = \frac{{\varepsilon^{3} d_{p}^{2} }}{{150(1 - \varepsilon )^{2} }} $$
(10)

Recently, the authors showed[15] that the CFD model using the Brinkman–Forchheimer drag coefficient (β) cannot accurately model the experimentally obtained pressure drop values of the well-sealed 30, 50, and 80 PPI alumina CCFs. The average errors were reported to be in the range of 85.14 to 87.29 pct for the well-sealed 30, 50, and 80 PPI alumina CCFs. On the contrary, the empirically derived Darcy and non-Darcy terms, the same first- and second-order coefficients in the Forchheimer equation (Eq. [1]), could model the experimentally obtained pressure gradients with the average error of only 4.15, 1.56, and 4.41 pct for the well-sealed 30, 50, and 80 PPI alumina CCFs, respectively. Therefore, the same approach was employed to simulate fluid flow in the unsealed samples. As a result, the Forchheimer drag term (β F) defined by Eq. [11] was applied instead of the Brinkman–Forchheimer drag coefficient (β) in Eq. [4].

$$ \beta_{\text{F}} = \frac{\rho }{{k_{2} }} $$
(11)

In addition, the following assumptions were made in the statement of the mathematical model: (1) the fluid density, temperature, and dynamic viscosity were assumed to be constant; (2) the filters in the 2D axisymmetric models were assumed to be fully cylindrical; (3) the gravitational force was neglected (the filters were positioned horizontally in the experiment); and (4) the pipe surface was assumed to be smooth and frictionless.

Boundary Conditions and Mesh Optimization

The same boundary conditions and mesh optimization technique used in mathematical modeling of the well-sealed samples[15] were also applied for the CFD modeling of the unsealed samples. Table III shows the complete list of the boundary conditions for the system.

Table III Boundary Conditions[15]
Full size table

Four types of mesh, defined in Table IV, were analyzed at maximum outlet fluid velocity to evaluate if the solution converges and if the highest average mesh quality can be achieved.[15] The CFD predicted and experimentally obtained pressure gradient data at three fluid velocity rates are compared in Table V. The differences between the CFD predicted pressure drop values were not significant, ranging from 0.012 to 0.13 pct. As explained elsewhere,[15] the computational time and the mesh quality were used as criteria to select the suitable mesh option. Therefore, mesh option 3 was selected to perform CFD simulations, since a reasonable result within an adequate computational time and a high average mesh quality (0.9332) could be achieved.

Table IV Minimum and Maximum Mesh Size Options[15]
Full size table
Table V Effect of Mesh Size on CFD Predicted Pressure Gradient of Sealed 80 PPI Model
Full size table

Results

Permeametry Experiments

The obtained pressure gradient profiles as a function of fluid velocity for the well-sealed and unsealed 30, 50, and 80 PPI samples are shown in Figure 4. The figure presents pressure gradient profiles of the fully sealed samples (dark solid curves), the unsealed samples (the dotted curves), and the previous studies by Kennedy et al.[8] labeled as P (the light solid curves). Each presented number in the new experimental work represents an average of minimum 24, 26, and 31 readings with a confidence interval of 95 pct for the 30, 50, and 80 PPI filters, respectively. As presented in Figure 5 for an 80 PPI filter, the minimum and maximum margins of error for the pressure gradient data lie in the range of 0.59 to 0.85 pct and 1.29 to 6.16 pct for the fluid velocity.

Fig. 4
figure 4

Measured pressure gradients of the well-sealed (dark solid curves) vs the unsealed samples (dotted curves) of single 30, 50, and 80 PPI filters[9,15] and previous studies labeled as P[8] (light solid curves)

Full size image
Fig. 5
figure 5

Measured pressure gradient of the fully sealed single 80 PPI filter (dark solid curve) with a confidence interval of 95 pct margin of error (dotted curves)

Full size image

The current experimental procedure is similar to Kennedy’s work. The only differences compared to the recent work were applying a slightly different sealing procedure, and taking experimental samples of alumina CFFs from the same manufacturer but from different batches, and different sized commercial filters.[15]

The Darcy (k 1) and non-Darcy (k 2) permeability coefficients of the well-sealed and unsealed CFFs were estimated based on the experimentally obtained pressure gradients and the calculated mean fluid superficial velocity rates. The permeability coefficients were empirically estimated in accordance with the Forchheimer equation (Eq. [1]). As explained in Section II, the Darcy and non-Darcy coefficients for both the well-sealed and unsealed samples were acquired using the Ergun’s approach, i.e., dividing the Forchheimer equation (Eq. [1]) by velocity and applying a linear regression.[8,15,33] The calculated k 1 and k 2 values and the deviations between the well-sealed and unsealed coefficients are summarized in Table VI.

Table VI Calculated k 1 and k 2 Values of the Fully Sealed and Unsealed Single 50-mm-Diameter Samples
Full size table

Mathematical Modeling

Three scenarios were examined to investigate the effect of bypassing on permeability parameters of the 30, 50, and 80 PPI CFFs:

  1. (1)

    modeling the well-sealed permeametry experiments using the empirically derived k 1 and k 2 values from the permeametry experiments of the well-sealed samples;[15]

  2. (2)

    modeling the unsealed permeametry experiments based on the empirically obtained k 1 and k 2 values from the permeametry experiments on the unsealed samples; and

  3. (3)

    modeling a condition when the empirically derived k 1 and k 2 values of the unsealed experimental trials are used in a model representing the sealed condition.

Scenarios 1 and 2 were used to simulate the actual experimental conditions. However, scenario 3 aimed at investigating a condition when no sealing procedure is applied and the empirically derived Darcy and non-Darcy coefficients are treated as the “adequate” permeability parameters of the filters. This approach, i.e., using unsealed or inadequately sealed samples in permeametry experiments, was observed in several articles during the literature review.

Figures 6 and 7 present the mathematically modeled well-sealed and unsealed permeability experiments for an 80 PPI CFF. As explained in Section II and shown in Figure 6 for a well-sealed model, fluid enters the modeled pipe section from one side and flows through the filter and leaves the filter and pipe from the opposite side. The arrows in the figure show the direction of the flow. In an unsealed model, fluid is allowed to enter the pipe, filter, and gap from one side, flow freely through the filter and gap, and leave the pipe, filter, and gap from the opposite side (Figure 7).

Fig. 6
figure 6

2D axisymmetric 80 PPI CFD model of a well-sealed filter at 0.28 m/s outflow velocity

Full size image
Fig. 7
figure 7

2D axisymmetric 80 PPI CFD model of an unsealed filter at 0.27 m/s outflow velocity

Full size image

The measured and CFD predicted pressure gradients as a function of superficial velocity for the well-sealed and unsealed 30, 50, and 80 PPI filters as well as the results of the mathematical model explained in scenario 3 are shown in Figures 8 through 10. More specifically, Figure 8 presents the deviations between the experimentally obtained (solid curves) and CFD predicted (dotted curves) pressure gradients of the well-sealed filters. Figure 9 shows the deviations between the experimentally obtained (dashed curves) and CFD predicted (dotted curves) pressure gradients of the unsealed filters. Figure 10 illustrates the measured pressure gradients of the well-sealed (dark solid curves) and unsealed (dashed curves) 30, 50, and 80 PPI samples. The figure also presents comparison between the measured pressure gradients and CFD predicted pressure gradients of the sealed model (dotted curves) using the experimental data of the unsealed samples.

Fig. 8
figure 8

Measured pressure gradients (dark solid curves) vs the CFD predictions (dotted curves) as a function of superficial velocity as well as the deviation between the experimental data and CFD predictions for the well-sealed 30, 50, and 80 PPI samples.[15]

Full size image
Fig. 9
figure 9

Measured pressure gradients (dashed curves) vs the CFD predictions (dotted curves) as a function of superficial velocity as well as the deviation between the experimental data and CFD predictions for the unsealed 30, 50, and 80 PPI samples

Full size image
Fig. 10
figure 10

Measured pressure gradients of the well-sealed (dark solid curves) and unsealed (dashed curves) 30, 50, and 80 PPI samples as a function of superficial velocity vs the sealed model CFD predictions (dotted curves) using the experimental data of the unsealed samples

Full size image

Discussion

The pressure gradient profiles as a function of superficial velocity for the well-sealed and unsealed 30, 50, and 80 PPI CFFs were experimentally obtained. A considerable deviation exists between the two pressure gradients in all filter types (Figure 4). The average deviations between the two gradients were calculated to be 57.2, 56.8, and 61.3 pct for the 30, 50, and 80 PPI CFFs, respectively. The lower pressure gradients observed in the unsealed CFFs are due to fluid bypassing from the gap between the filters and filter holder. The gap provides a path of least resistance to fluid flow, causing bypassing along the wall of the unsealed samples. Therefore, no sealing or inadequate sealing would result in underestimation of the pressure gradient at any given flow rate.[8,9,15] The figure also compares the recent results to the previous permeability studies performed on samples taken from alumina CFFs by Kennedy et al.,[8] as explained elsewhere;[15] the previous results could be reproduced. The empirically obtained Darcy (k 1) and non-Darcy (k 2) permeability coefficients of the unsealed 30, 50, and 80 PPI CFFs reveal deviations to the permeability coefficients of the well-sealed samples. The deviations are caused by underestimated pressure gradients due to fluid bypassing in the unsealed samples.

The CFD estimated pressure gradients of the well-sealed filters were found to be in good agreement with the experimentally obtained pressure gradients (Figure 8). The deviation was calculated to be in the range of only 0.3 to 5.5 pct for all three PPI types of filters.[15] The bias between the experimental and CFD estimated pressure gradients is believed to be due to the assumption made for CFD studies; i.e., the modeled filters possess a perfectly cylindrical shape.[15]

The CFD calculated pressure gradients of the unsealed 30, 50, and 80 PPI samples also showed good agreement with the experimental results (Figure 9). The deviations to the experiment were calculated to be in the range of 3 to 8 pct for 30 and 50 PPI samples and 17 to 21 pct for 80 PPI samples. The main source of the deviations is believed to be due to the application of the empirically obtained Darcy (k 1) and non-Darcy (k 2) permeability coefficients in the CFD module. Here, the empirically derived k 1 and k 2 values represent both the filter and gap. However, in the CFD module, the values could be assigned only to the filter. In addition, the higher deviations in 80 PPI might be due to the dimensions of the 80 PPI filter sample as well as the nature of the filter. More specifically, the 80 PPI sample has slightly smaller diameter and larger thickness than the 30 and 50 PPI samples, as shown in Table II. Therefore, more fluid bypassing and lower pressure gradients could result, i.e., the gap available for fluid bypassing would be to some extent larger and the pressure gradient would be calculated based on a larger thickness. Moreover, the 80 PPI filters contain much smaller openings, compared to 30 and 50 PPI filters.[8,15,48] In an 80 PPI filter, fluid requires higher pressure to pass through the openings. This could result in more fluid bypassing from the gap between the filter and filter holder if the filter is not fully sealed.

The mathematically obtained pressure gradients according to scenario 3, i.e., using the permeametry experimental data of the unsealed sample in a model representing the sealed condition, were compared to the experimentally obtained pressure gradients of the well-sealed and unsealed 30, 50, and 80 PPI filters. The CFD estimated pressure gradients based on scenario 3 deviate from the experimentally obtained pressure gradients of the well-sealed samples, as one may expect. The deviation was calculated to be in the range of 50 to 60 pct. However, the CFD estimated pressure gradients of scenario 3 lie on or very close to the experimentally obtained pressure gradients of the unsealed samples (Figure 10). This also can be considered as confirmation that neglecting the sealing procedure results in underestimation of the pressure gradients.

Conclusions

The Darcy and non-Darcy permeability coefficients of the well-sealed and unsealed single 30, 50, and 80 PPI commercial alumina filters were empirically derived using liquid permeametry experiments. The data were used to mathematically model the well-sealed and unsealed experimental trials by using COMSOL Multiphysics 5.1. The CFD estimated pressure gradients were also compared to the experimental data. The main conclusions from the recent research are summarized as follows:

  1. 1.

    The pressure gradients of the unsealed 30, 50, and 80 PPI CFFs revealed a considerable deviation of 57.2, 56.8, and 61.3 pct to the well-sealed CFFs.

  2. 2.

    Sealing procedure was found to be necessary for accurate estimation of the permeability parameters of the filters. In order to avoid bypassing, it is essential to completely seal the specimen and to fill the gap between the sealed samples and filter holder.

  3. 3.

    The empirically obtained Darcy coefficients (k 1) of the unsealed 30, 50, and 80 samples showed a 9, 20, and 31 pct deviation to the well-sealed 30, 50, and 80 samples.

  4. 4.

    The empirically obtained non-Darcy coefficients (k 2) of the unsealed 30, 50, and 80 samples showed a 59, 58, and 63 pct deviation to the well-sealed 30, 50, and 80 samples.

  5. 5.

    The CFD predicted pressure gradients based on the empirically obtained Darcy and non-Darcy permeability coefficients are in good agreement with the experimental data for both the well-sealed and unsealed CFF samples. Specifically, the deviations to the experimental data were in the range of 0.3 to 5.5 pct for all three PPI types of the well-sealed filters. The deviations to experimental data were found to be in the range of 3 to 8 pct for 30 and 50 PPI and 17 to 21 pct for 80 PPI unsealed filters.