Slag foaming has been studied for decades due to its important role in both the Linz–Donawitz converter (LD-converter) and the electric arc furnace.[1–6] Slag foaming is a very complicated phenomenon involving a number of phases, possibly (1) gas phases, (2) liquid phase(s), and even (3) solid phases.[2,7,8] The complexity of foaming slag is one of the foremost hindrances for the researchers to understand the mechanism of slag–metal reactions in the LD-converter. Whether the reactions in the processes take place mostly between the steel droplets and the foaming slag or at the interface between the slag and steel bath has for long been an interesting topic.[9] A better understanding of the foaming slag will help clarify this issue, which is essential for any sound dynamic process model. Very interesting behaviors have recently been noticed in the foam generated by passing argon gas through silicone oil.[10] The foamed silicone oil shows shear-thinning non-Newtonian behavior; and the apparent viscosities measured show values of 2 to 5 times higher than the dynamic viscosity of the silicone oil. As a continuation, the present work studies the behavior of slag foams at elevated temperature. The focus is twofold, namely (1) the structure of the slag foam, whether it is similar to the foam of silicone oil and (2) the apparent viscosity of the slag foam. The foam is generated by letting the slag react with hot metal and graphite powder to form CO and CO2.

The slag composition was chosen based on the LD-converter slag, namely CaO(43mass pct)-SiO2(32mass pct)-FeO(25mass pct). The FeO was produced first by mixing Fe2O3 and pure iron powder and then sintering the mixture at 1123 K (850 °C) for approximately 70 hours in a closed iron crucible in argon atmosphere. The sintered FeO was then crushed into small pieces. A premelted CaO(54 mass pct)-SiO2(46 mass pct) slag was used as the master slag. The slag was adjusted to the target composition by addition of FeO and calcined CaO.

The experimental setup is schematically shown in Figure 1. An induction furnace with a water-cooled copper coil was employed to heat the sample to the experimental temperature, viz. 1873 K (1600 °C), and the sample temperature was maintained throughout the measurement. Since thermocouples would be affected by the magnetic field induced by the furnace,[11] an infrared temperature sensor (model thermoMETER CTM-1SF75-C3) was used for temperature measurement. The sensor was calibrated with a pyrometer of model Raytek Thermoalert ET before use. Because the variation in magnetic fields changes the temperature in short distances, the temperature could therefore be somewhat different in the middle part of the sample where the magnetic field was more intense, compared to the top or bottom part of the sample. However, with the purpose of studying the trends of the apparent viscosity in the foam, an uncertainty of ±50 K was considered acceptable.

Fig. 1
figure 1

Experimental setup

Full size image

Due to the different viscosity range, a Brookfield RVDV-II+Pro was used for the slag foam measurements, while a Brookfield LVDV-II+Pro was used for the pure slag measurements. The latter is suitable for viscosities of lower ranges. The viscometers were calibrated right before use by a service center. The spindles were made of molybdenum and designed with conic bottoms to make sure they would not float on top of the slag or bring air down to the sample. The bob of the spindle was 15 mm in diameter and 7 mm in height. The conic tip of the spindle had a height of 4 mm, see Figure 1.

To study the foaming slag, graphite crucibles were used with a wall thickness of 10 mm. The graphite crucible had 30 mm inner diameter and an inner height of 130 mm. In view of the uncertainty introduced using graphite components in viscosity measurement for liquid slag, molybdenum crucibles were used to determine the viscosity of liquid slag without foaming. All crucibles were painted on their outer surface with yttrium oxide paint, to protect the crucible against heavy oxidation. In the case of the experiment using molybdenum crucible, a protection tube made of quartz was used and argon gas was passed through the tube to further prevent oxidation. For each foaming experiment, 7 g of hot metal (consisting of 3.9 mass pct carbon) and 1 g of graphite powder was put in the bottom of the crucibles, then 67 g of the mixed slag was put on top.

The foaming started already 4 minutes after the induction was turned on, and was stable for approximately 2 minutes. Figure 2 presents a photo showing that foam is generated. The viscosity measurement started immediately when foaming was observed, using 25, 40, and 60 RPM. Note that only one rotation speed was used for each foaming slag to minimize the effect of slag composition on the measurement.

Fig. 2
figure 2

Photo showing slag foaming

Full size image

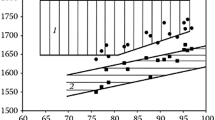
The results of the viscosity measurements show that the foam does not act as a Newtonian fluid. Instead, a shear-thinning non-Newtonian behavior is observed, where the apparent viscosity is lower at higher spindle rotation speed. This aspect is well brought out by the experimental results shown in Figure 3. Similar behavior has also been reported in literature[12] and in a previous work.[10] Non-Newtonian fluid is difficult to model, and its viscosity is hard to predict since the viscosity varies with different shear rates. It should be mentioned that the results may vary with the experimental setup and conditions, depending on the wall effects, type, and dimensions of the spindle and temperatures. Therefore, no attempt was made in the present study to generate quantitative data for foam viscosities. The main focus of the experimental effort was to study the trends of viscosity in a foam and to compare it with the pure liquid (slag without foam). For this purpose, the results shown in Figure 3 could be very informative when they are used in a relative manner. As shown in the figure, the reproducibility of the experiments is very reasonable when the experimental conditions are fixed. At a rotation rate of 60 RPM, two independent measurements lead to values of 0.30 and 0.33 Pa·s, which are in good accordance. Figure 3 also reveals evidently an increase in apparent viscosity in the foam compared to the pure liquid slag. The apparent viscosity is measured between 0.3 and 0.5 Pa·s in the foam, while it is only measured to 0.095 Pa·s in the pure liquid slag, which is in accordance to the literature.[13,14]

Fig. 3
figure 3

Apparent viscosity of foaming slag

Full size image

It should be mentioned that the uncertainty in temperature in the present setup is about ±50 K. According to Slag atlas,[14] the dynamic viscosity of the present initial slag is 0.15 Pa·s at 1673 K (1400 °C) compared with the value of 0.095 Pa·s at 1873 K (1600 °C). This small difference is not compactable with the great increase in viscosity when foam is generated. In view of the FeO reduction, the slag composition after the foaming experiment was analyzed using X-ray fluorescence analysis (XRF). The average composition was 48 mass pct. CaO, 36 mass pct. SiO2, and 16 mass pct. FeO. According to the available data,[14] the dynamic viscosities of the initial slag and the slag after reduction are 0.15 and 0.2 Pa·s at 1673 K (1400 °C), respectively. This change is negligible comparing with the profound viscosity increase of the foamed slag.

It is worthwhile to mention that the residence time of metal droplet in the foaming slag is always a topic of steelmakers. Very often, the residence time is evaluated using the dynamic viscosity of the slag. As revealed by Figure 3, the use of dynamic viscosity in the evaluation of residence time would lead to great error. Since the moving velocity of a droplet is expected low, the values measured using low rotation speed of the spindle would be more relevant. The use of dynamic viscosity to evaluate the residence time would result in a residence time at least 4-5 times shorter than that in the real foaming slag.

The much higher apparent viscosity of slag foam compared with pure liquid slag is in good agreement with the finding in the case of cold model experiments, where silicone oil and argon gas are employed.[10]

As discussed in the previous work,[10] the energy needed to deform an interface between liquid and gas is higher than the energy needed to deform the bulk liquid. This finding is in fact in good agreement with the literature.[15] A semiquantitative calculation is made in the previous work.[10] Assuming no volume change, when a sphere with radius of 1 mm is compressed into a spheroid with height c = 0.7 mm, the deformation leads to an increase of 6.4 pct in surface energy. The silicone oil used has a surface tension of 2.1 × 10−2 J m−2. For a spherical bubble with dimension r = 1 mm, the surface energy change due to deformation would be 1.02 × 10−7 J, since the movement of a particle would involve approximately the deformation of 6 bubbles (at minimum) at the same time. The work against the viscous force needed to move the particle through the pure liquid was found to be approximately 20 pct of the surface energy change for deformation of the bubbles. This semiquantitative calculation explains well the experimental result of silicone oil.

The results shown in Figure 3 has further confirmed this reasoning. It reveals that even in the foaming slag, the surface energy plays an important role, since the apparent viscosity is much bigger than the dynamic viscosity of the liquid slag.

However, the apparent viscosity of the foaming slag should have been much bigger if the foams of the slag and the silicone oil were similar and the reasoning in the previous work were applicable to the slag, since the surface tension of slag is much higher than the silicone oil. On the other hand, this expectation is not met by the results in Figure 3. To gain an insight into this difference, a comparison of the foam structures is necessary.

In a number of experiments, the foaming slag was frozen by simply turning off the induction. The foam was solidified in only 2 to 3 seconds after this turning off. Figure 4 presents the cross sections of two typical frozen foam samples. The figure shows evidently that in great contrast to the foam of silicone oil, the bubbles do not distribute in the foam uniformly. Another huge difference between the slag foam and the silicone foam is the liquid. In the case of the foam of silicone oil, small bubbles (1 to 2 mm in diameter) distribute uniformly throughout the whole foam layer, in which each bubble has a thin liquid oil film surrounding the gas phase. The thin liquid film is not seen in the slag foam. Small liquid “bulks” are present all over the foam along with the gas bubbles. In other words, the gas is not separated by liquid films. The bubbles distributed in the liquid phase creates a two-phase mixture, but not a bubble structure. The sizes of the bubbles shown in Figure 4 differ also from the foam of silicone oil. A careful microscopic examination reveals that the bubble size in the slag foam varies from 0.1 mm up to 4 mm. This is in strong contrast with the silicone foam, where all the bubbles are in the range between 1 and 2 mm.

Fig. 4
figure 4

Two pieces of foaming slag

Full size image

The ratio of the gas volume over the total volume of the foam (V gas/V tot) is much higher for the silicone oil foam in comparison with the slag foam. For the foaming slag, the ratio is estimated to be approximately 0.35 using point counting,[16] while for the silicone oil foam, the ratio is approximately 0.7. As a matter of fact, this difference could easily be seen visually. The lower (V gas/V tot) of the slag foam in comparison with the silicone foam would suggest that the role of surface energy change due to the movement of any particle in the foam would be less profound compared to silicone foam, though this role is still more important than the dynamic viscosity. A similar estimation of the impact of surface energy change on the apparent viscosity as in the case of silicone oil would be difficult, since it would need the knowledge of the size distribution of the gas bubbles entrapped in the slag.

The present results reveal confidently that the surface tension has much bigger impact on the apparent viscosity and therefore on the movement of particles in the foam in comparison with the dynamic viscous energy. The required surface energy change could slow down the particle movement greatly in a foaming slag. The difference in foam structure between silicone oil and slag (see Figure 4) indicates that while the cold model study using silicone oil is very useful, the conclusion obtained should be used with certain precaution when applied to slag system. It is strongly felt that substantial experimental work is needed to really understand the droplet movement in a foamed slag. As a matter of fact, the present communication would like to provoke the efforts toward this understanding.