Introduction

Fusion welding techniques have been utilized in the structural joining of safety-critical components across aerospace,[1] automotive,[2] and power generation[3,4] industries for many years, thanks to the considerable joint-integrity that they can offer, and their relatively low capital investment and production costs.[1] Whilst older welding methods such as tungsten inert gas (TIG) produce large weld pools and heat-affected zones[5] due to the size of the arc formed, the newer “high power-density” beam-type processes, such as laser welding, offer a much narrower fusion zone and heat-affected zone,[6] as the energy from the power source is much more focused.

Welding simulation has been considered by academia and industry alike for many years; however, with the constantly increasing computational power available to the researcher, the details of the models and their outcomes have become more and more intricate over the years. Newer modeling methods, including multi-physics modeling which can take into account the solid, liquid, and vapor phases of materials, liquid flow lines, Marangoni forces, surface tension effects, buoyancy effects and compressible or incompressible fluids have been developed and utilized.

The computational fluid dynamics (CFD) approach is used to simulate the interaction of the heat source and the materials considering the transition between liquid and solid states as well as between the liquid and vapor states. These solid-liquid and liquid-gas interfacial conditions are of importance to be comprehensively understood as they can contribute to the formation of residual stresses and distortions during the welding operation. Over the last two decades, literature has been reported on sophisticated modeling approaches[7–12] and experimental techniques[13–18] to study the dynamics of the keyhole phenomena during high power density fusion welding technologies, such as laser welding. From a modeling perspective, the interface deformation that leads to keyhole formation during the laser welding has been studied intensively using various numerical techniques, including a volume-of-fluid approach[13,14] and a level set method.[9] Recently, Courtois et al.[9] have proposed a level set approach and included the influence of the electromagnetic field to accurately capture the energy reflection inside the keyhole. However, the methodology is very computationally expensive. To reduce the computational time and resource, one might use a simplified version, to provide a sensible timescale for obtaining the weld pool dimension with various processing inputs. Panwisawas et al.[19] have proposed a keyhole model, which can be used to predict the melt pool geometry as a function of processing conditions, reflecting the melt flow behavior during the welding operation.

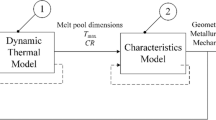
Whilst the CFD modeling can predict complex fluid flow and interface phenomena, coupling of this model with a finite-element approach is required in order to achieve the detailed predictions about the mechanical behavior. The CFD model can potentially offer a very detailed knowledge about the driving forces behind the various phenomena observed within welding, which can be very difficult to measure using instrumented experimentation alone. However, one of the primary drivers for weld simulation, especially within industry, remains the prediction of welding-induced distortions and residual stresses. Distortion and residual stress predictions are beyond the scope of a CFD code, as they require structural calculations typical of a finite element (FE) code. Therefore, it becomes very desirable to link together a CFD-type model, capable of predicting the fluid flow and process physics within a molten weld pool, with an FE-type model capable of predicting the mechanical response of the plate or component exposed to the weld pool. Finally, an integrated computational materials engineering (ICME) framework is required to make predictions for the component microstructural properties. A link between the outputs of the finite element code and microstructural parameters can be considered, typically using outputs from FE such as heating/cooling rates, as these are the principal drivers for a number of microstructural properties.

Current FE methods typically require some a priori knowledge of the weld pool shape anyway, which is typically obtained from an experimental weld performed at the particular welding parameter set required for the conditions for the relevant material and geometry, such that an experimental weld line can be produced and cross-sectioned for measurements. This clearly reduces the predictive capability of the modeling approach, as it requires this experimental input. Thus, the capability to predict the weld pool shape via another model which can be linked in to the FE model significantly improves the predictive capabilities of weld simulation.

Method

The C++ open source Open Field Operation and Manipulation (OpenFOAM) package has been utilized to develop a keyhole model using two incompressible, non-isothermal immiscible fluids using a volume of fluid (VOF) phase-fraction-based interface capturing approach. A detailed description of the model adopted can be found in the previous work of Panwisawas et al.[19] The thermal fluid dynamics calculation is computed based upon the evolution of the thermal field coupled with the Navier-Stokes equation for fluid flow. The flow calculation has included vaporization (recoil pressure), solid-liquid and liquid-vapor phase changes, surface tension, and thermal-capillary effects or Marangoni flow; moreover, an adaptive volumetric heat source model modified from literature[20] has been used to simulate the energy reflection inside the keyhole. Heat loss due to conduction, convection, and radiation has been physically captured at the metallic/gaseous interface. However, despite the simplification of this fluid and thermal dynamics model when compared to others, run-times are still relatively long. For optimal performance, the OpenFOAM CFD model was constructed to consider a thin plate weld, thus reducing as much as possible the number of elements required. This work has considered the Ti-6Al-4V plate to be of 1mm thickness. This same plate geometry is therefore considered when results are passed through to a FE model for mechanical analysis. An example of the predicted weld pool, shown in both isometric and a cross sectional views, is seen in Figure 1.

Fig. 1
figure 1

Outputted weld pool shape from the CFD OpenFOAM model. As seen at an isometric angle, and analyzing a cross section perpendicular to the direction of travel

Full size image

Using this CFD modeling framework,[19] a series of CFD models were performed (Table I), considering the heat source traveling through a thin plate (a typical bead-on-plate weld) with varying process parameter sets (welding speed and welding source power). The predicted thermal results were used to predict a representative weld pool size and shape for each of the welds. The CFD model was run for long enough in each case to establish a so-called “steady-state” weld shape. As has been discussed previously, the CFD model illustrates some interesting features of a laser-beam weld pool, notably the fact that it never truly achieves steady-state because the vapor pressure inside the keyhole is highly unstable, meaning that the keyhole region of the weld is constantly pulsing and momentarily collapsing in on itself. But, from a fusion-zone boundary perspective, the weld pool does indeed reach a stable size and shape, whereby the fixed fusion boundary is maintained at a steady size and shape, and the molten pool traverses through the material at the source travel speed. CFD models were calculated on a HPC cluster, parallelized over 4 cores, and each model had a run-time of ~4-5 days. Each CFD model can be interrogated to understand the size and shape of this fusion boundary. Whilst the CFD model will of course give a complete, full 3D representation of the predicted weld pool shape, some pragmatism must be adopted when attempting to fit this weld pool shape in to the FE model. For this stage of the work, the specialist welding FE code SYSWELDTM, from software company ESI, was selected.

Table I Parameters Used for the Welds Considered in this Work
Full size table

SYSWELD has been developed as an FE weld simulation tool over several years. As a software package, it has been demonstrated to offer excellent predictive capabilities regarding distortions and residual stresses. SYSWELD does have a number of limitations, however, specifically in the definition of the weld pool formed as result of the material interacting with the heat source. SYSWELD typically requires the molten pool to be described as either a Goldak double-ellipsoid function[21,22] or a Gaussian (conical) function.[23,24] However, It is also possible to directly enter a set of Cartesian x,z co-ordinates to describe the ½ width of the weld pool (in the x-axis) (assuming a symmetrical weld shape) at any given depth (the z-axis), about the widest region of the molten weld pool in its y axis (length).[25] The widest region of the cross-sectioned weld pool is considered to be the location at which the heat source beam (either laser or EB) is contacting the material. The software will then make a best attempt to maintain the fusion boundary at these specified Cartesian co-ordinates by heating the enclosed material above the liquidus temperature. The software also requires to be provided with the energy per unit length (\( \varphi \)) at the weld line. This is calculated from

$$ \varphi = \frac{IV}{u} $$
(1)

where I and V are the electrical current and voltage of the laser system (thus, the product I·V is the power), and u is the source travel speed. Clearly, both the key welding parameters considered in this study, welding source power, and travel speed, have a direct impact upon the energy per unit length to be distributed, with a higher power obviously directly proportional to energy per unit length, and travel speed inversely proportional to energy per unit length. SYSWELD is typically run in a weakly coupled mode, so the thermal analysis is completed and each time step saved, before the thermal results are used in the calculation of the mechanical analysis.

The baseline FE model was set up using a 30 mm wide by 20 mm long by 1-mm-thick plate, with the weld line to be traversed in the center of the plate, running up the length. As shown in Figure 2a. The mesh was set to contain 0.05-mm width brick elements within the region 1.5 mm either side of the weld, and a graded mesh increasing to 2.5 mm in width. All elements were a uniform 0.5 mm in length and 0.125 mm in depth. The weld source was passed along the entirety of the weld path, and following the welding operation, 100 seconds of cooling time elapsed. The models were subsequently analyzed for their post-cooling residual stress profiles and their distortion profiles.

Fig. 2
figure 2

(a) Model Set-up, showing graded mesh and weld path. (b) Schematic showing the angular distortion mode (butterfly distortion) observed in a typical bead-on-plate weld

Full size image

Using this baseline model, each weld simulation was created identically, apart from the relevant welding speed, weld energy per unit length and heat source model, which was based upon the outputs from the previously reported CFD model, by taking the width of the assumed symmetric weld pool at 0.1 mm intervals throughout the depth of the plate. Clearly, the SYSWELD requirement for a symmetric weld pool means that some small assumptions must be made, i.e., the minor amounts of asymmetry about the weld path observed in the CFD model results were negligible and these were caused by numerical instabilities only. Models were computed on an Intel i5 desktop computer, parallelized over 4 cores, with a typical run-time of 1 hour per thermal-mechanical simulation.

In order to validate the coupled CFD–FE modeling strategy, experimental welding trials using bead-on-plate laser welds were performed upon samples of 1 mm thickness plates of Ti-6Al-4V titanium alloy to determine the angular distortion observed experimentally (Figure 2b). The welds were performed using a Trumpf TruDisk laser system, which employs a fiber laser with a wavelength of ~1030 nm and a beam spot size of ~800 µm in diameter. These facilities are at the University of Birmingham. The Ti-6Al-4V titanium alloy plates were purchased from Ti-Tek UK Ltd, Birmingham. Four of the welds modeled in the coupled CFD–FE framework were performed on the Trumpf laser cell for experimental validation. Validation of the thermal fields predicted by coupled modeling was considered in previous work.[25] However, a mechanical validation exercise is presented here to assess the accuracy of the coupled model against experimental data.

Results

Thermal results for the series of 9 weld simulations were reported in the literature previously.[25] The capability of this heat source representation, using Cartesian co-ordinates to specify the fusion boundary, has been demonstrated, and is illustrated in Figure 3. The critical outputs from the thermal simulation include the replication of the size and shape of the weld pool predicted by the CFD model, in the FE software. Given that the CFD model weld pool predictions show a considerable amount of tapering in their widths at different depths, the ability of the FE software to reproduce substantial tapering in the width is encouraging. Peak temperatures inside the pool are of less importance than the fusion boundary. As the FE software has no knowledge of the liquid phase material properties, it is unavoidable that the absolute temperatures predicted inside the weld pool must be based upon extrapolated data from the solid-state phase; thus, they are less reliable. However, given that the pool shape and size entirely dictate the residual stress and distortion, errors in the predicted peak molten pool temperatures are relatively unimportant (Table II).

Fig. 3
figure 3

Cross sections showing the variation in weld pool shape for varying laser power and varying source travel speed for all 9 weld simulations

Full size image

The predicted thermal profiles were subsequently used to compute the mechanical response to the thermal loading. Of key interest to welding engineers are the resulting distortions and residual stress fields left within the welded component as a result of these thermal loads. The corresponding mechanical results (notably the calculated Von Mises Residual stress field and the angular mode distortion due to the vertical distortion field) have been computed and analyzed. A summary of these mechanical and thermal results are presented in Table II. The predicted Von Mises residual stress fields for all 9 weld simulations are presented in Figure 4. A Von Mises residual stress distribution perpendicular to the weld line, along the plane of analysis (as indicated in Figure 2), was extracted for each weld model. These distributions are presented in Figure 5. The resulting stress fields suggest that the characteristic double-peaked stress profile is observed for all welds, with the two peaks at the very edge of the weld bead, where the material never quite reached the solidus temperature or re-set the stresses to zero. Clearly, inside the weld bead, stresses are slightly lower, given that any initial stress formation was wiped out once the material became molten, and only started accumulating stresses again upon solidification.

Table II Results from the Welds Considered in the Work
Full size table
Fig. 4
figure 4

Residual stress fields for varying laser power and varying source travel speed for all 9 weld simulations

Full size image
Fig. 5
figure 5

Line plots of Von mises residual stress profiles across the plate, taken from the mid-section of the plate

Full size image

The width of the highly stressed region depends upon the width of the molten pool, and hence naturally the width of this region changes slightly from weld to weld, based upon the process parameters, with the slowest, highest power input weld containing the widest highly stressed region, and the fastest, lowest power weld displaying the narrowest region of high stresses along the weld stripe. The predicted peak values of von Mises residual stress within the welded plate, at the edge of the fusion boundary, show substantial variations, dependent upon the welding parameters. Whilst the models for the 100 mm/s weld and the 200 mm/s welds all predict peak von Mises stresses within a narrow band of one another—520 to 560 MPa, a variation of ~7.5 pct or below, well within modeling errors for being considered a reasonably constant peak stress—the 50 mm/s weld models are predicting far higher von Mises residual stress values, of 948, 832, and 685 MPa for the 1.5, 2, and 3 kW welds, respectively. The slower traveling welds allow for greater heat to be distributed in to the metal, over a larger volume of material. Hence, the 50 mm/s welds consistently had higher predicted von Mises residual stress.

Perhaps contrary to what would seem logical, the lower power weld at 50 mm/s is predicted to have the highest residual stress. Given that von Mises stresses are largely driven by thermal gradients, and that the higher peak temperatures are observed in the higher power welds, acting over narrower regions, this cannot be rationalized. However, the results for residual stress should not be considered in isolation, and should in fact be considered alongside the distortion results. If we consider plate distortion as an inherent way of the part attempting to stress relieve itself, then these 3 weld simulations, at 50 mm/s, are predicted to have virtually no butterfly distortion mode. Thus, with no distortion to relieve some of the built-up stresses, they just continue to accumulate. The fact that these 2 welds are predicted to give no distortion at all would offer concerns that the plate has somehow become constrained due to the excessively wide weld bead.

Similarly, the angular deformation mode (sometimes called the butterfly deformation) created by the welding process was calculated from the distortions predicted by the SYSWELD code, for each of the 9 welds, and is presented in Figure 6. The distortion profile, plotted along the same plane as previously for the residual stress profile, was extracted and this is presented in Figure 7. In order to predict the butterfly distortion, three nodes within the left-side of the plate were assigned as the standard rigid-body clamping definition, to ensure that the plate behaved as a true rigid body. This is evidenced by the affixing of the left-edge of the plate to remain in its original location, whilst the right edge of the plate distorts accordingly, based upon the mechanical response to the thermal load. The resultant plate distortions illustrate that the maximum butterfly angle was predicted (2.3 deg) and measured (1.6 deg) for the lower power, fastest weld.

Fig. 6
figure 6

Vertical distortion fields (shown in mm) for varying laser power and varying source travel speed for all 9 weld simulations

Full size image
Fig. 7
figure 7

(a) Line plots of Vertical distortion profiles across the plate, taken from the mid-section of the plate. (b) Experimental measurement vs. FE prediction of the distortion profile across the plate for welds 6 (top-left), 7 (top-right), 8 (bottom-left), and 9 (bottom-right)

Full size image

Clearly, the weld which has the lowest energy per unit length has generated the greatest distortion, whilst the weld with greatest energy per unit length is predicted to display the lowest distortion. Again, this is perhaps a slightly counter-intuitive finding, given that it is often summarized that increasing the heat input increases distortion. However, titanium has a very low thermal conductivity, thus generally the heat inputted in to it remains in a similar size boundary, and does not dissipate very much. For a lower energy input, one would expect to see the heat remain in a neat, narrow band of molten material. This allows the thermal expansion of the material in this narrow region to provide a narrow “hinge” for the plate to distort at a high level, in an angular (butterfly) mode, whereas the wider zone of molten material means that there is not this high gradient in stiffness perpendicular to the welding stripe, and as such there is much less angular distortion observed within the plate when a substantially wider weld pool is considered.

Four of the bead-on-plate welds were scanned using a Keyence LJ-V7080 laser triangulation line scanner mounted on a Trumpf gantry robot. The scan resolution across the light plane was 50 μm, and the speed of motion along the plates was synchronized to the scan rate to give 50 μm resolution in that direction too. The laser-scanned plate surfaces were coated with a spray of Boron Nitride to reduce the scatter of the laser due to the shiny surface. Unfortunately, the weld line region still produces significant scatter of light, thus producing a lot of noise in the data at the weld line region. By comparison of the modeled predictions for mechanical distortion to those measured by experimental scanning (Figure 7b), an understanding of the accuracy of modeled predictions can be made. The welds 6, 7, 8, and 9 were chosen for validation experiments as they showed some of the largest distortions in the FE models.

It becomes evident from the comparison (see Table III; Figure 7b) that the coupled CFD–FE model is over-predicting the angular distortion mode for the 200 mm/s welds, although marginally under-predicting for the 100 mm/s weld. In relative terms, the FE model is predicting the correct trends observed from experiment. The model correctly predicts that the combination of lowest power and highest travel speed (weld 7) produces considerably larger distortions than any other weld. This is due to the fact that the weld bead in this instance has a much more tapered shape than other beads. Weld 7 was predicted by FE model to not quite be a fully penetrating weld (see Figure 1), and this prediction was confirmed by experiment. In absolute value terms, the over-prediction of the model is typically 0.4 to 0.8 deg for the fastest welds. The likely cause of the modeling over-prediction is the extrapolated material data used within the finite element calculation for Ti-6Al-4V properties such as thermal expansion at temperatures exceeding the liquidus point, as it becomes extremely challenging to measure the material properties at such elevated temperatures.

Table III Comparison of Coupled Model Predictions Against Experimental Data
Full size table

A process map has been created based upon the FE predicted results, to highlight the welding parameter combinations that appear susceptible to predicting high levels of residual stress (Figure 8) and distortion (Figure 9). Given that residual stress and distortion are the common causes for part non-conformance, these types of process maps would offer a welding engineer an immediate sweet-spot to target, or a danger zone to avoid, when planning a welding process.

Fig. 8
figure 8

A contour map showing the influence upon Von mises residual stress (in MPa) by the 2 key process parameters (Weld speed and Power)

Full size image
Fig. 9
figure 9

A contour map showing the influence upon the butterfly angle (in deg) by the 2 key process parameters (Weld speed and Power)

Full size image

In order to make microstructural predictions, a link between the cooling rate experienced by the solidifying material (as it passes through the beta-transus temperature) and the mean lamellar spacing within the microstructure was obtained, from a number of literature sources.[26–28] An approximate power-law trendline was fitted to the data, \( \lambda = 1.726 \delta^{ - 0.276} \), where λ is the lamellar spacing (in μm) and δ the cooling rate as the material passes through the β-transus temperature (in K) such that any estimated cooling rate could be directly linked to an associated lamellar spacing. By considering each of the 9 weld models during the steady-state traversing of the weld pool through the material, the nodes in the immediate wake of the heated material could be analyzed, at the relevant time-step, to determine their cooling rates. A contour map of the associated mean lamellar spacing, as a function of the 2 key process variables (welding speed and welding power), is given in Figure 10. The predicted mean lamellar spacing within the solidified weld line of the part is shown to vary between 0.1 and 0.3 μm. The resulting process map gives a clear indication regarding the values of the process parameters to be targeted for specific lamellar spacing requirements.

Fig. 10
figure 10

A contour map showing the predicted influence upon the microstructural lamellar spacing, by the 2 key process parameters (Weld speed and Power)

Full size image

Given the resulting mechanical responses predicted by the FE models, it is likely that the wide variation in the key process parameters considered here that many of these welds would result in several of these welds being unsuitable for production. It is likely that only a relatively small number of these welds are performed at sensible parameters such that distortions and residual stresses are maintained at sensible levels. However, this demonstrates the flexibility and robustness of the modeling framework developed, such that it is not only applicable in a relatively small envelope of process parameters that give successful welds, but can also be expanded in to the undesirable process parameters, and still maintain computational robustness and speed.

Summary and Conclusions

A framework for the coupled modeling of beam welding in a simple, 1-mm-thin plate has been established. A CFD model has been developed in OpenFOAM for weld pool shape and size prediction, which takes into account the physical behavior including all interfacial phenomena and energy reflection. This has been linked with the finite element welding simulation SYSWELD, to perform the structural analysis of the 1-mm-thick welded plate. Validation experiments were carried out for modeling capability assessment. In turn, the finite element outputs have been linked to a microstructural model that can predict lamellar spacing in the solidified weld bead. By interrogation of this model, the following conclusions are drawn:

  • Linking of a CFD model for predicting weld pool size and shape to an FE code to simulate mechanical response has proven feasible. This link is most efficiently established using simple Cartesian co-ordinates to determine approximate weld pool width for a series of depths in to the material, although this is software dependent.

  • Weld pool shapes observed from the CFD model OpenFOAM can be reasonably well reconstructed in the FE software, and the fusion zone boundary can be made to taper substantially in the waist of the weld bead, and flare out again at the base. In terms of accurately predicting stresses and distortions, capturing the varying weld pool width at various depths is of great importance. However, capturing these weld pool width variations through the depth is highly dependent upon having a mesh fine enough in these regions close to the boundary of the fusion zone.

  • Process maps have been generated, based upon a small matrix of 9 weld simulations, highlighting “hot-spots” for predicted high residual stress values (low weld speed and low power) and predicted higher butterfly angular distortion modes (high weld speed and low power). Given that residual stress and distortion are of importance to manufacturers, targeted areas to be avoided, and the associated process parameters which lead to these, are equally of importance.

  • A simple microstructural model, based upon data from literature, has been used to link the predicted cooling rate as the material passes through the β-transus temperature to the mean lamellar spacing formed in the cooled microstructure. A similar process map has been developed, to highlight how combinations of the 2 key process variables (welding speed and power) will influence the cooling rate, and in turn the lamellar spacing, and offer guidance to parameters if a particular lamellar spacing is desired.